基于鲁棒极端学习机的混沌时间序列建模预测∗

沈力华 陈吉红 曾志刚 金健†

1)(华中科技大学机械科学与工程学院,武汉 430074)

2)(华中科技大学自动化学院,武汉 430074)

1 引 言

混沌是发生在自然界确定系统中貌似不规则、类似随机的运动[1−3].从实际系统中获得的具有混沌特性的时间序列种类和数量越来越多,如大气环流、气温、降雨量、太阳黑子、黄河流量等[4−6].近年来,针对混沌时间序列的预测与分析已成为当今科学研究领域的一个研究热点[7−9].由于神经网络和支持向量机较强的非线性逼近能力,其已被广泛应用于混沌时间序列建模预测中,如:多层感知器[10]、回声状态网络[11]、正则化回声状态网络(RESN)[12]及鲁棒回声状态网络[4]、模糊神经网络[13]、极端学习机[14]、贝叶斯极端学习机(BELM)[15]、支持向量极端学习机(SVELM)[16]、递归预测器神经网络(RPNN)[17]等,都在混沌时间序列的预测中取得了快速的发展.

上述方法中,极端学习机由于其具有结构简单、学习效率高且能得到全局最优解等优点而得到广泛应用.极端学习机随机初始化输入权值,在训练过程中只调整输出权值,从而可以得到全局最优解,且具有更快的收敛速度,克服了梯度消失等缺点.由于上述优点,近年来针对极端学习机的改进算法得到了快速的发展,如:有学者提出多核极端学习机(MKELM),以充分表达被学习数据集的信息[5,18],基于智能优化算法的极端学习机[19]通过优化核参数及模型其他全局参数来提升算法的预测性能,基于在线学习的极端学习机[20]以及面向深度学习的极端学习机[21].

极端学习机通过将输入变量映射到高维空间,使数据在高维空间中具有线性特性,再对高维空间中的数据进行处理.目前,极端学习机最常采用的训练方法为伪逆法.伪逆法虽然简单易于实现,但其在实际应用中容易产生病态解,即出现输出权值很大的情况,导致模型的泛化能力很弱.为解决病态解问题,文献[22]提出正则化极端学习机(RELM),在极端学习机优化目标函数中引入正则项,通过选取合适的正则化参数,提高模型泛化性能,避免了病态解问题.但是正则化参数的确定往往采用交叉验证方法,而交叉验证方法计算量较大且非常耗时.BELM不需要采用交叉验证方法便可自动实现模型参数的估计,同时能够提供模型参数的概率预测,进而得到预测的置信区间.但BELM假设模型输出似然函数为高斯分布,这一假设使得模型对于含有异常点的时间序列非常敏感,当训练数据中含有异常点时,模型预测精度会受到很大影响.而在实际应用中,由于数据受多种噪声共同影响,数据中往往存在异常点.因此,建立一种对噪声和异常点不敏感的鲁棒极端学习机(Robust-ELM)预测模型在实际应用中具有重要意义.

采用重尾分布的模型输出似然函数,使模型对异常点具有较强的鲁棒性,高斯混合分布作为一种近似Student-t分布,对异常点仍具有鲁棒性[23].以单变量分布为例,在不含有和含有异常点两种情况下,高斯分布以及高斯混合分布的概率密度曲线如图1和图2所示.取自高斯分布的300个整数点的直方图分布,及其基于高斯分布和高斯混合分布的最大似然估计曲线如图1所示.将26个异常点加入到上述数据集中产生的相应直方图分布及基于不同分布的最大似然估计曲线如图2所示.从图2可以看出,高斯分布对异常点非常敏感,而高斯混合分布具有较强的鲁棒性,不易受异常点的影响.因此,本文采用高斯混合分布作为模型输出似然函数.

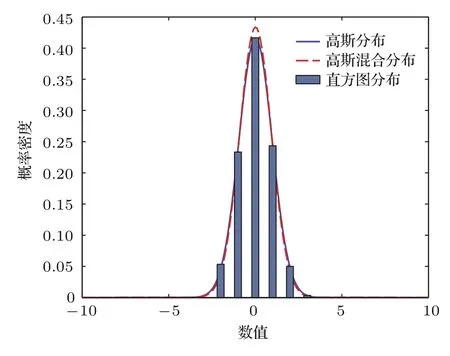
图1 无异常点时不同分布概率密度曲线Fig.1.Probability density curves of different distribution without outliers.

将高斯混合分布作为模型输出似然函数,使得模型输出边缘似然函数变成难以解析处理的形式,因此,引入变分近似推理对模型参数进行估计,实现模型的训练,从而得到一种Robust-ELM.所提模型不但具有极端学习机的非线性逼近能力和BELM自动学习模型参数的能力,同时对异常点具有较强的鲁棒性.与统计物理学采用的方法相似,本文同样采用概率统计的方法来实现物理量的分析.在含有噪声和异常点的情况下,将所提模型应用于大气环流模拟模型方程Lorenz序列、Rossler序列以及太阳黑子混沌时间序列等物理量的预测中,通过仿真实验分析,证明了所提模型对于解决含有噪声和异常点的时间序列物理量预测问题,具有一定的价值和意义.

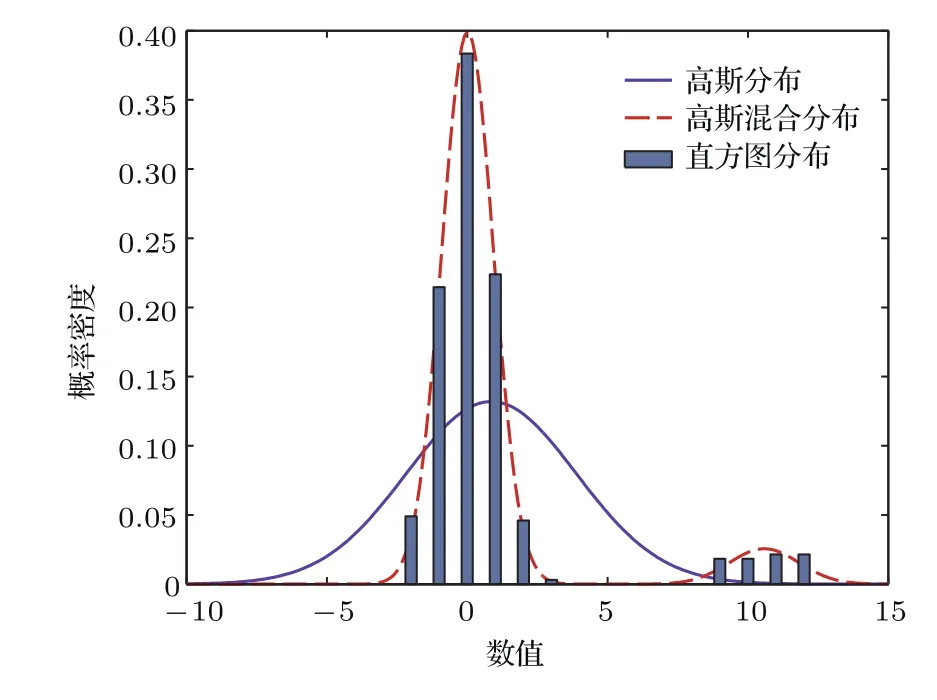
图2 含异常点时不同分布概率密度曲线Fig.2.Probability density curves of different distribution with outliers.

2 极端学习机

2.1 极端学习机预测模型

极端学习机是一种单隐层前馈神经网络,它由三层结构组成,分别为输入层、隐层及输出层,其结构如图3所示.其中,输入层和中间层、中间层和输出层分别由输入权值和输出权值连接,输入权值随机产生,在网络学习过程中不进行调整.极端学习机通过隐层将输入变量映射到高维空间,使输入变量在高维空间中具有线性特性,再通过学习输出权值,对高维空间状态进行线性表示,最终逼近输出变量.

对于任意给定的N个不同样本(xi,ti),其中为样本输入,ti为样本目标输出,为样本目标输出变量,设隐层节点个数为n,隐层激活函数为g(x),一般为sigmoid函数.图3极端学习机输入输出公式如下:

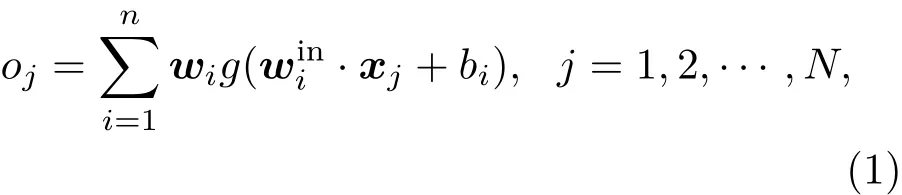
式中,oj为预测输出;为第i个隐层节点与输入层节点之间的连接权值,在网络训练之前随机产生;为第i个隐层节点与输出节点间的连接权值;表示点积运算.当有样本输入到网络中时,采用激活函数和连接权值逼近N个样本的目标值,则可得到下式:

式中,

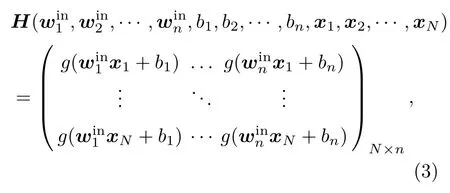
其中,

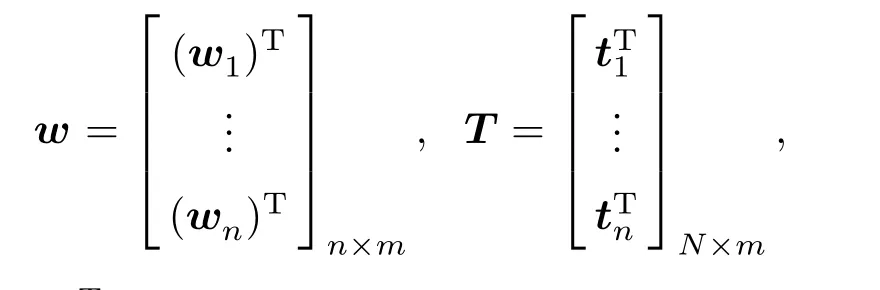
当HHT或HTH非奇异时,输出权值w通过下式求取,

H†表示H的伪逆,当rank(H)=N时,H†=HT(HHT)−1; 当rank(H)= n 时,H†=(HTH)−1HT.当HHT或HTH奇异时,可通过奇异值分解法求得w.

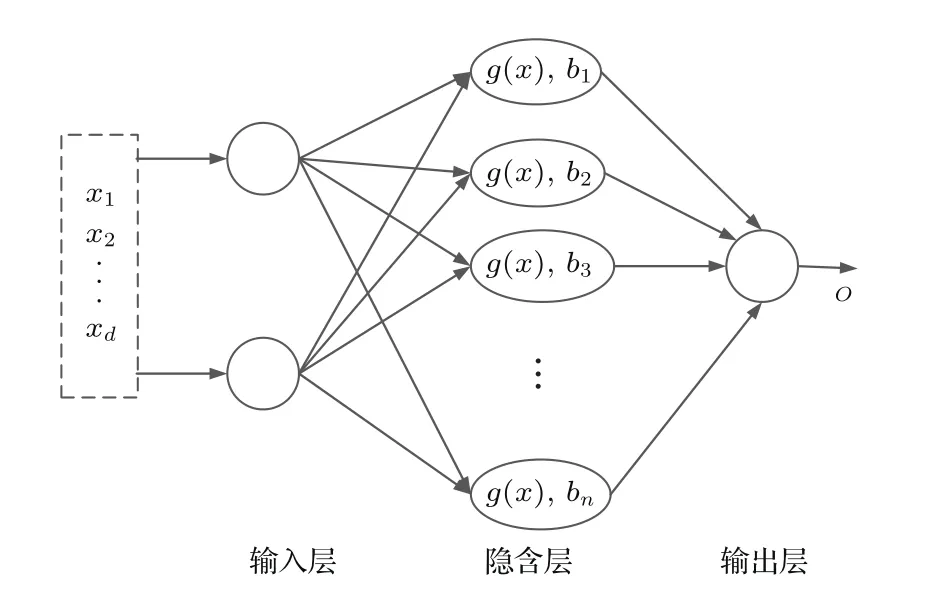
图3 极端学习机结构Fig.3.Structure of extreme learning machine.

在实际应用中伪逆法容易产生病态解,即出现输出权值很大的情况,导致模型的泛化能力很弱.解决上述问题的正则化方法在网络优化目标函数中引入正则项,通过最小化如下目标函数求得网络权值w:

通过将问题转化为拉格朗日对偶优化问题,得到的网络输出权值为

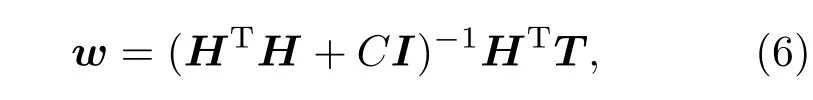
其中I为n×n的单位矩阵,C为正则化参数.正则化参数C的确定通常采用交叉验证的方法,计算量较大,且不易得到最优值.

2.2 BELM

BELM可以通过自动递归求得输出权值,不需要采用交叉验证方法确定正则化参数,同时能避免伪逆法容易产生病态解的问题.该方法假设学习误差独立且服从零均值高斯分布,即训练数据似然函数服从如下高斯分布:

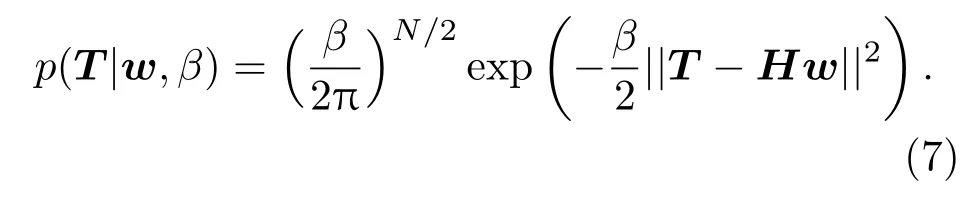
网络输出权值的先验分布设为

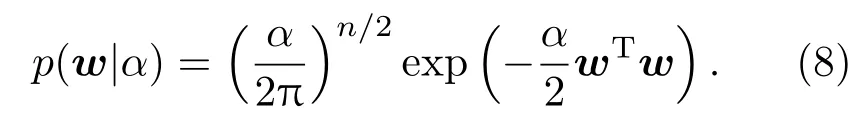
w的相应后验分布同样为高斯分布,其均值和方差矩阵分别为mN和SN:

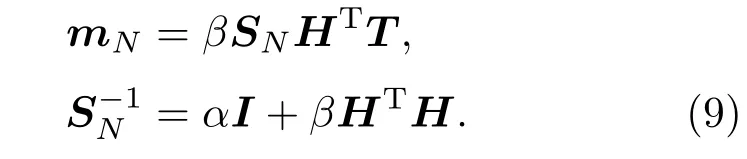
通过证据近似法确定β和α的值,计算公式如下:

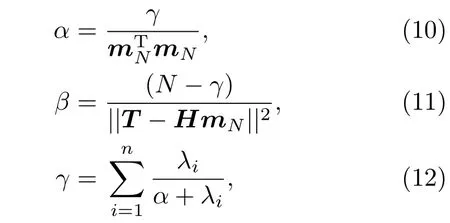
其中,λi为βHTH的特征值.首先初始化参数β和α,再利用初始化后的β和α计算mN和SN,如(9)式所示,再利用估计的mN和SN,按照(10)和(11)式重新计算β和α的值,如此重复计算直到算法收敛.

3 Robust-ELM

上述基于贝叶斯回归的极端学习机,实现了网络参数的自动学习,不需要通过交叉验证确定正则化参数,但是贝叶斯回归假设网络学习误差独立且服从零均值高斯分布,该模型对异常点不具有鲁棒性,当数据中存在异常点时,会使得模型的预测精度受到很大影响,因此本文在贝叶斯学习框架下,提出一种具有鲁棒性的极端学习机预测模型.

3.1 Robust-ELM推理与参数估计

Robust-ELM将训练样本输出似然函数设置为高斯混合分布,如(13)式所示.高斯混合分布也是一种重尾分布,它是Student-t分布的一种近似形式,具有对异常点不敏感的特性,对于任意一个训练样本,具体形式如下:

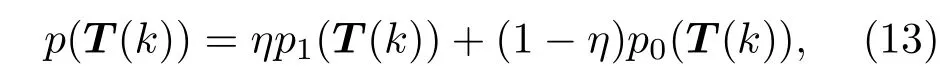
其中p1(T)如(7)式所示,p0(T)如下:

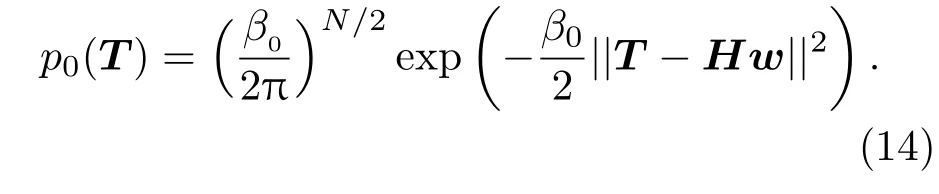
对于所有训练样本输出似然函数可写成

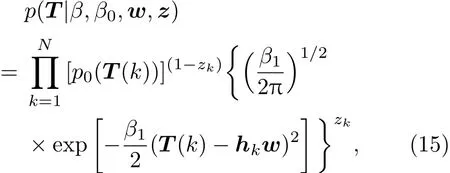
其中,hk为H的行向量,隐变量z的概率分布为

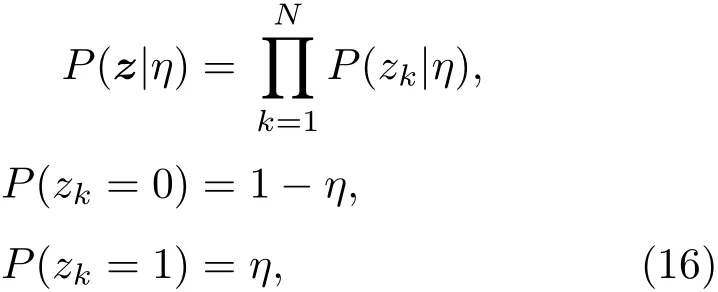
不同于BELM,在Robust-ELM中,将w的先验概率分布设置为

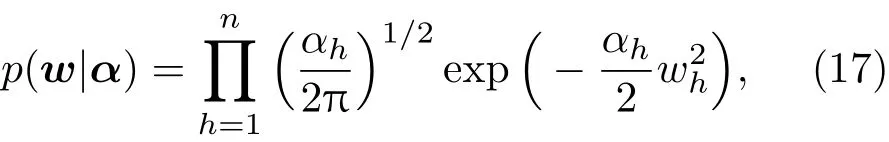
式中,αh和wh分别为α和w的第h个元素,极端学习机隐层节点数.先验分布的设置类似于相关向量机中将α设置为由不同值组成的对角阵,而非一个标量,使得模型输出权值具有稀疏解,提高了模型的泛化性能[24].

模型输出的边缘似然函数可表示为

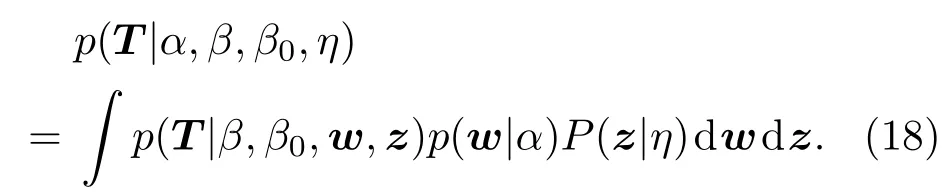
由于(18)式是难以解析处理的,因此采用变分法近似推理,得到隐变量z和网络输出权值w的后验概率分布.利用变分推理方法[25],求得网络输出权值w的近似后验概率分布为高斯分布,其协方差矩阵和均值分别为Σ和µ.

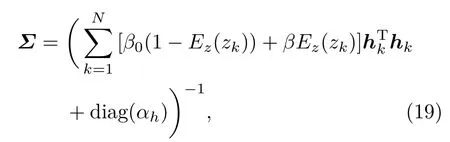
其中,Ez(zk)为zk关于分布z的期望,

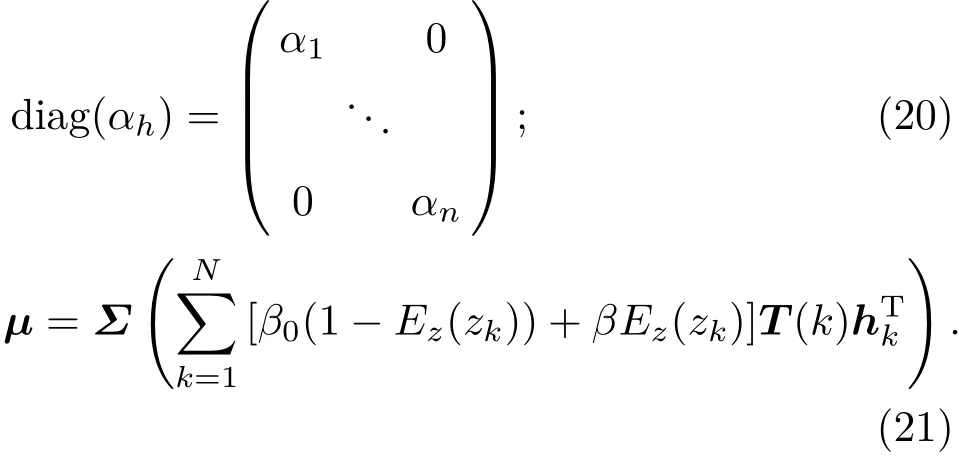
隐变量z的概率分布为

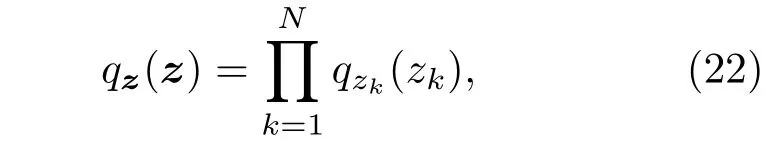
式中,

其中,

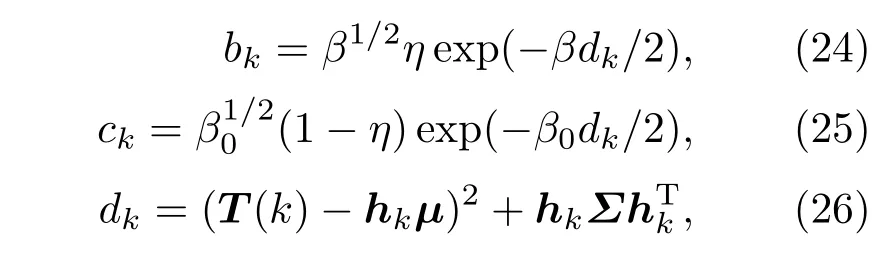
为更快速地更新各参数值[25],参数更新公式如下:

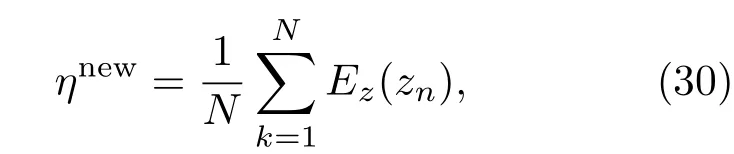
其中,µh和Σhh分别为µ和Σ的第h个元素.

3.2 Robust-ELM实现步骤

Robust-ELM预测模型首先将输入变量映射到高维空间,进行鲁棒贝叶斯推理,再利用变分近似推理法求得网络输出权值w.

模型具体实现过程如下.

第一步,随机初始化极端学习机输入权值矩阵win,并选择适当的隐层节点数n,得到高维序列矩阵H.

第二步,将极端学习机输出矩阵w作为待估参数,设其先验概率分布为(17)式,极端学习机输出似然函数为(15)式,隐变量z的概率分布为(16)式.

第三步,基于变分推理方法,对Robust-ELM网络输出权值进行估计:

1) 初始化αh(h=1,2,···,r),β,β0,η及qzk(zk),初始化后,将以下步骤2和步骤3执行υ1次,υ1为主更新次数;

2)采用上述初始化后的各参数值,利用(19)式计算协方差矩阵Σ,再利用求得的Σ ,通过(20)式计算均值µ,获得µ后再继续利用计算协方差矩阵Σ,如此循环υ0次,υ0为子更新次数;

3)利用(27),(29)和(30)式实现参数αh,β及η的更新,参数更新法收敛.

第四步,将第三步估计得到的µ作为Robust-ELM网络的输出权值w,当有新样本需要预测时,将新样本通过第一步极端学习机隐层映射到高维空间,并利用(2)式得到其预测值.

上述实现步骤可通过图4表示.

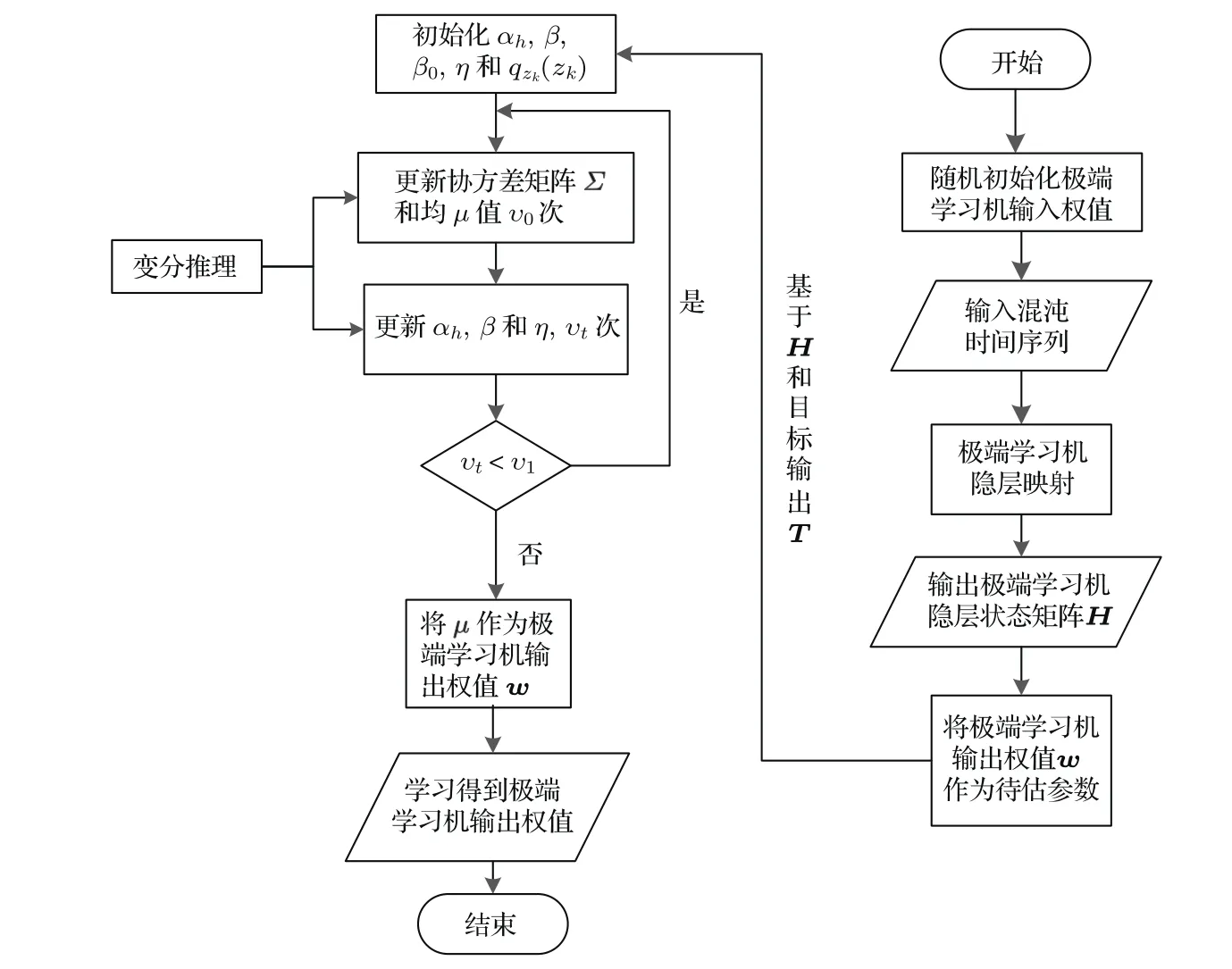
图4 Robust-ELM实现流程Fig.4.Implementing flow of Robust-ELM.

4 仿真实验

为验证所提模型的有效性,将其应用于加入噪声和异常点的大气环流模拟模型Lorenz混沌时间序列预测、Rossler混沌时间序列和太阳黑子时间序列预测中,并采用均方根误差(root mean square error,RMSE)定量评价所提模型的性能,其中oi为第i个样本的预测值,ti为第i个样本的实际值.

为验证所提Robust-ELM的有效性,在三组仿真实验中,通过向时间序列加入不同比例的噪声和异常点来进行仿真实验.加入噪声和异常点的方式分为6种:方式A为只加入数量为训练样本1%的10倍异常点,不加入高斯噪声;方式B为只加入10%水平的高斯噪声,不加入异常点;方式C为加入10%水平的高斯噪声和训练样本2%数量的10倍异常点;方式D为加入20%水平的高斯噪声和训练样本5%数量的20倍异常点;方式E为加入30%水平的高斯噪声和训练样本8%数量的30倍异常点;方式F为加入40%水平的高斯噪声和训练样本10%数量的40倍异常点.具体加入噪声和异常点的方式为:在训练数据集的目标变量中加入一定水平的高斯噪声,并随机选择一定比例的训练样本,再将选择到的训练样本原值通过相应比例的放大以加入异常点.以加入方式D为例;加入20%水平的高斯噪声和5%的20倍异常点是指加入20%水平的高斯噪声的同时,再从训练样本中随机选择Noutlier(Noutlier为训练样本总数乘以5%经四舍五入后取整)个样本,将这Noutlier个样本的值放大20倍.

将Lorenz,Rossler和太阳黑子-黄河流量时间序列加入噪声和异常点后,将其与RELM[21],RESN[12],BELM[15],SVELM[16],MKELM[18]和基于改进微粒群算法的核极端学习机(APSOKELM)[19]等方法的预测结果进行比较.并选取训练集20%的数据作为验证集,以确定各模型的全局最优参数值.在三组仿真实验中,Robust-ELM方法的主要参数设置如表1所列.

表1 Robust-ELM模型的主要参数设置Table 1.Parameters setting of Robust-ELM.

4.1 Lorenz混沌时间序列仿真分析

Lorenz系统是美国气象学家Lorenz模拟大气环流模型建立的三元一阶常微分方程组[2],Lorenz混沌方程如下

随机选择初始值,舍弃瞬态后产生训练集和测试集,将得到具有混沌特性的时间序列.为使得相关算法在同等条件下进行比较,将初始值设置为a=10,b=8/3,c=28,x(0)=y(0)=z(0)=1.0.利用四阶Runge-Kutta法产生2500组混沌时间序列.将x(t),y(t),z(t)作为输入序列,x(t+1)作为待预测序列,选择前1800组作为训练样本,后700组作为测试样本,Lorenz时间序列如图5所示.

图5 Lorenz混沌时间序列(a)Lorenz-x(t)时间序列;(b)Lorenz-y(t)时间序列;(c)Lorenz-z(t)时间序列Fig.5.Lorenz chaotic time series:(a)Lorenz-x(t)time series;(b)Lorenz-y(t)time series;(c)Lorenz-z(t)time series.

表2 含不同比例噪声和异常点的各模型预测误差(Lorenz序列)Table 2.Prediction errors of different models for data with different ratios of noise and outliers(Lorenz time series).

加入不同比例的噪声和异常点后各模型的预测误差如表2所列.从表2可以看出,当数据中包含异常点时,各模型预测精度都受到一定的影响,与SVELM和Robust-ELM相比,RELM,RESN,MKELM,APSO-KELM和BELM受异常点的影响更大.主要是因为SVELM通过松弛因子能够减小一部分噪声和异常点的影响,而Robust-ELM通过采用高斯混合分布作为模型输出似然函数,提高了模型的鲁棒性,从而获得了更高的预测精度.

以方式D为例,将训练数据集中的目标输出序列中加入20%水平的高斯噪声和5%(90个)的20倍异常点.加入噪声和异常点后的Robust-ELM预测曲线和相应的预测误差曲线如图6所示,从图6可以看出,即使加入了大量噪声和异常点,所提模型仍具有较高的预测精度.

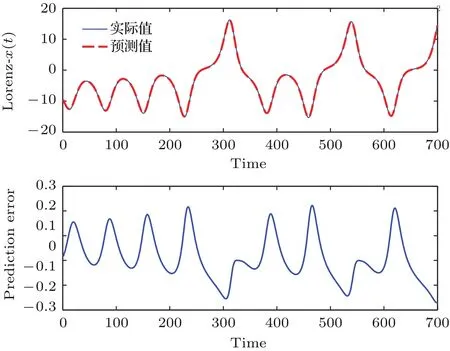
图6 含噪声和异常点的Lorenz序列x(t)预测结果(a)Robust-ELM预测Lorenz-x(t)曲线;(b)Robust-ELM预测误差曲线Fig.6.Prediction results of Lorenz series x(t)with noise and outliers:(a)Prediction curves of Robust-ELM for Lorenz-x(t)time series;(b)prediction error of Robust-ELM for Lorenz-x(t)time series.

4.2 Rossler混沌时间序列仿真分析

为更进一步的比较各算法的预测性能,另一组实验为Rossler混沌时间序列的仿真分析,Rossler时间序列方程如下所示:

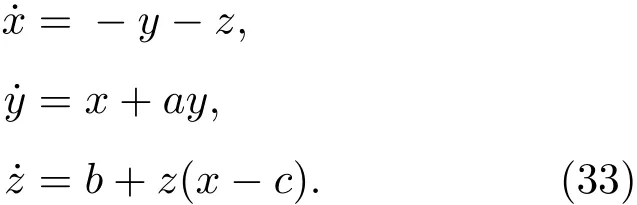
同样利用四阶Runge-Kutta法产生4000组混沌时间序列.将x(t),y(t),z(t)作为输入序列,x(t+1)作为待预测序列,选择前2000组作为训练样本,后2000组作为测试样本.为验证模型的有效性,同样采用6种方式加入不同水平的噪声和不同比例的异常点,加入噪声和异常点后不同模型的预测结果如表3所列.

从表3可以看出,采用方式B仅加入10%水平的高斯噪声时,APSO-KELM取得了最好的预测结果,主要是因为APSO-KELM通过改进的微粒群算法对核参数及其他全局参数进行优化,使得模型的预测精度有了较大提升,但当模型中加入异常点或同时加入异常点和噪声时,其预测精度受到了很大的影响,而所提模型只在方式B下预测精度仅次于APSO-KELM,在其他5种加入噪声和异常点的方式下,所提模型的预测结果都优于其他方法.从表3也可以看出,所提模型对高斯噪声和异常点均有较好的抗干扰能力,而对于异常点的抗干扰能力相对更强.以方式E为例,将训练数据集中的目标输出序列中加入30%水平的高斯噪声和8%(160个)的30倍异常点.加入噪声和异常点后的Robust-ELM预测曲线和相应的预测误差曲线如图7所示,从图中可以看出,即使加入了大量噪声和异常点,所提模型仍能较好地预测该时间序列值.

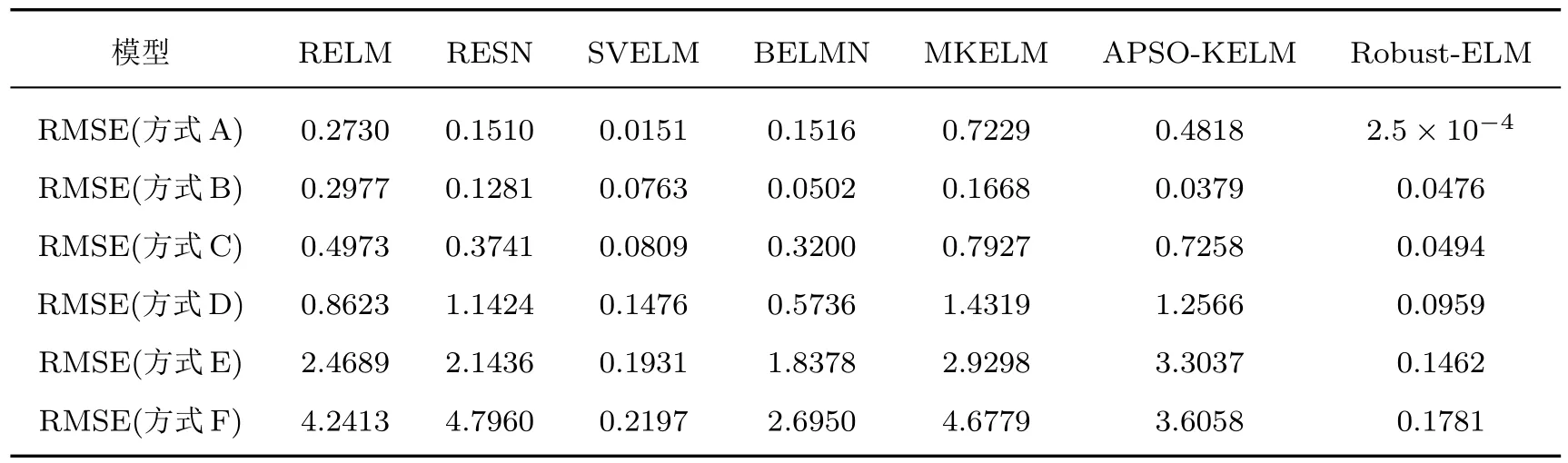
表3 含不同比例噪声和异常点的各模型预测误差(Rossler序列)Table 3.Prediction errors of different models for data with different ratios of noise and outliers(Rossler time series).

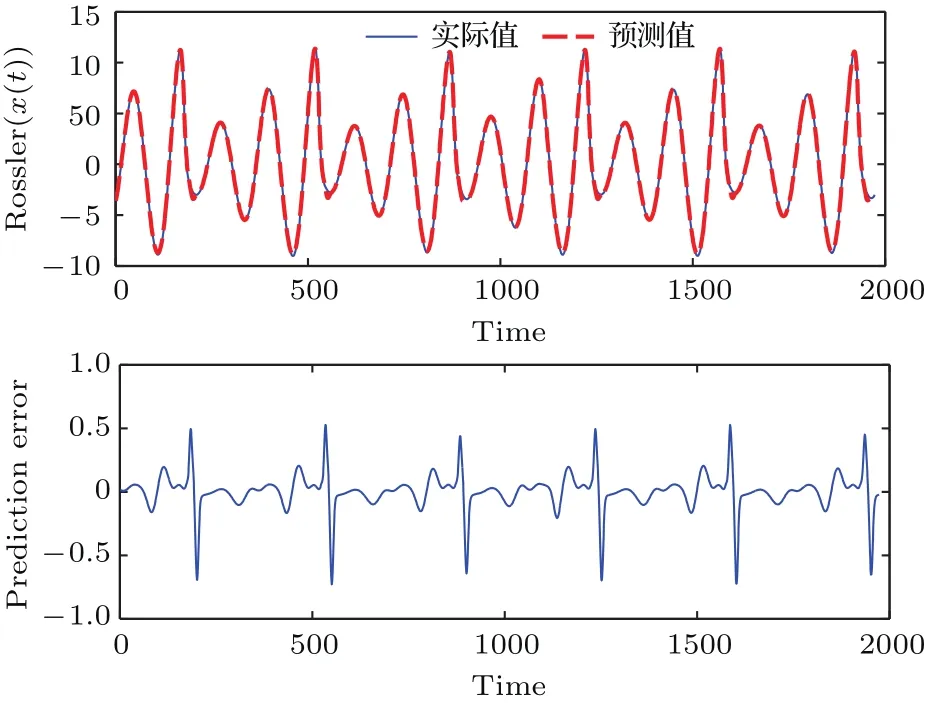
图7 含噪声和异常点的Rossler序列x(t)预测结果(a)Robust-ELM预测Rossler-x(t)曲线;(b)Robust-ELM预测误差曲线Fig.7.Prediction results of Rossler series x(t)with noise and outliers:(a)Prediction curves of Robust-ELM for Rossler-x(t)time series;(b)prediction error of Robust-ELM for Rossler-x(t)time series.

4.3 太阳黑子-黄河径流混沌时间序列仿真分析

为进一步验证所提模型的有效性,将其应用于太阳黑子和黄河径流二元混沌时间序列预测中,输入变量为太阳黑子和黄河径流量,待预测变量为下一年太阳黑子.选择样本区间为1700年至2003年太阳黑子和黄河径流量混沌时间序列.经相空间重构后,产生299组数据,选择前200组作为训练样本,后99组作为测试样本.

将训练数据集中的目标输出序列中加入异常点和噪声前后的太阳黑子时间序列如图8所示.

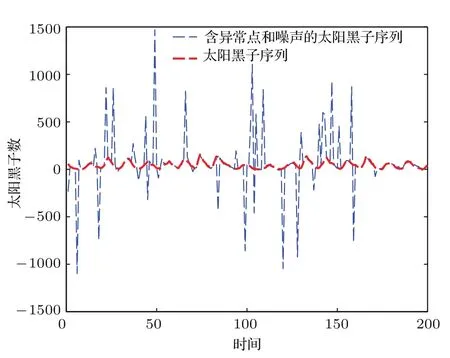
图8 含异常点和噪声的太阳黑子混沌时间序列Fig.8.Sunspot chaotic time series with outliers and noise.

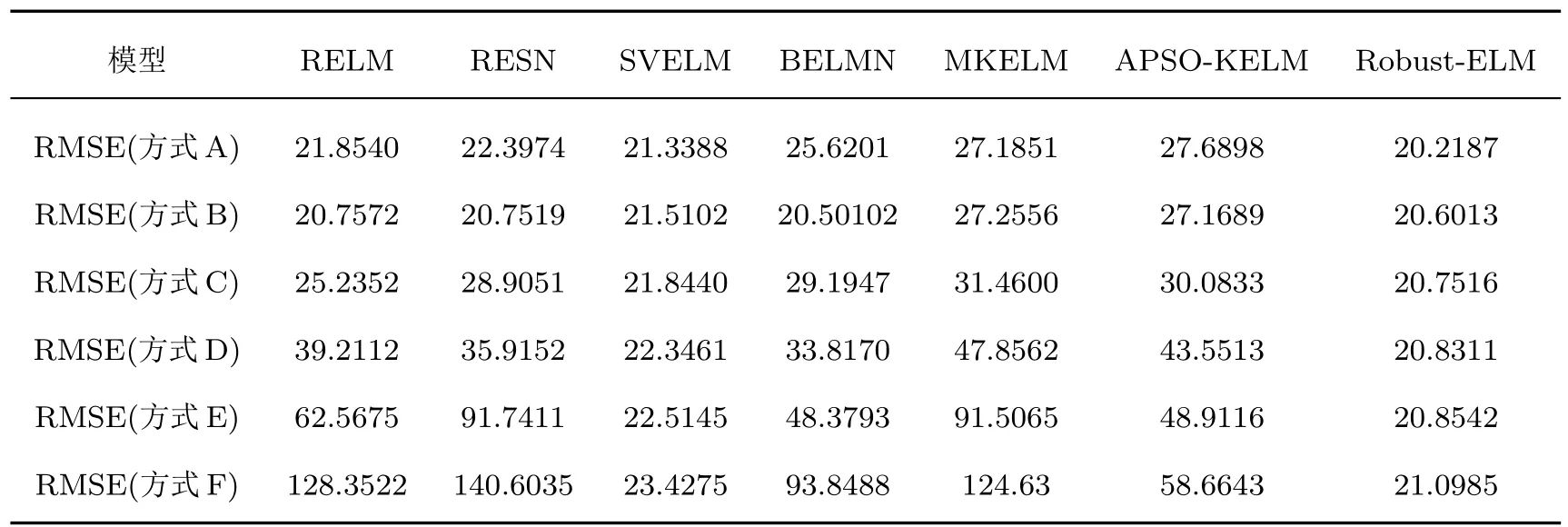
表4 含异常点和噪声数据的不同模型预测误差(太阳黑子序列)Table 4.Prediction errors of different models for data with outliers and noise(Sunspot time series).

加入不同比例异常点和噪声后各模型预测误差如表4所列.从表4可以看出,当加入大量噪声和异常点后,RELM,RESN,BELM和MKELM的预测精度受到了严重的影响,所提模型相比于其他方法仍具有更高的预测精度.从表4也可以看出加入噪声和异常点后所提模型预测值只产生了微小波动,具有较强的鲁棒性,能较好地描绘太阳黑子-黄河流量时间序列的动力学特性.

4.4 算法计算复杂度和收敛性分析

极端学习机模型对隐层状态矩阵HN×n直接求伪逆,计算复杂度为O(n2N+n3),其中N为训练样本数,n为极端学习机隐层节点数.所提Robust-ELM模型主更新次数为υ1,子更新次数为υ0,根据算法实现程序,执行υ1次迭代的时间复杂度为O(υ1υ0(Nn+Nn2+Nn3)), 括号中的Nn+Nn2+Nn3为执行一次子更新需要的向量与矩阵以及向量与向量相乘所需的总步数.

在实际应用中,训练样本数N一般大于隐层节点数n,因此,即使ELM时间复杂度与Robust-ELM均可表示为O(N),但在实际应用中,由于隐层节点数n的作用,Robust-ELM运行效率通常低于ELM.但在时间复杂度均为O(N)的情况下,Robust-ELM从算法的鲁棒性方面对已有算法进行改进和优化.其采用高斯混合分布作为模型输出似然函数,得到一种对异常点和噪声更具鲁棒性的预测模型.同时在三组仿真实验中,通过向时间序列加入不同比例的噪声和异常点来进行仿真实验分析,可看出Robust-ELM的预测性能远优于极端学习机,具有较强的鲁棒性.且在实际应用中,时间序列往往受到噪声和异常点的影响,因此,提高预测模型的鲁棒性,减小噪声和异常点对模型的影响对于提高模型预测精度具有重要的意义.

本文基于贝叶斯框架提出Robust-ELM,首先通过将输入样本映射到高维空间中,并将极端学习机的输出权值作为待估计参数,将具有重尾分布特性的高斯混合分布作为模型输出似然函数,再采用变分方法实现模型参数的估计.所提方法本质是基于变分贝叶斯推理估计模型参数,获得模型参数的后验概率分布.因此,其收敛性与变分贝叶斯估计相同,变分贝叶斯估计的收敛性在文献[26]中得到了详细的证明,详细的证明过程见文献[26]的附录A至附录F.与期望最大化迭代算法相似,所提方法采用设定阈值的方法确定最大迭代次数.在模型训练过程中,若当前次训练误差比上一次迭代时的训练误差之差小于该阈值时,说明算法已收敛.在三组仿真实验中,Lorenz序列的最大主更新次数为6,子更新次数为6;Rossler序列的最大主更新次数为7,子更新次数为5;太阳黑子序列的最大主更新次数为8,子新次数为6.以Lorenz序列为例,选择有代表性的方式D(加入20%水平的高斯噪声和训练样本5%数量的20倍异常点)、方式E(加入30%水平的高斯噪声和训练样本8%数量的30倍异常点)、方式F(加入40%水平的高斯噪声和训练样本10%数量的40倍异常点)向时间序列中加入噪声和异常点.在以上三种情况下,Robust-ELM算法的收敛曲线如图9所示,从图中可以看出,当主更新次数为4,即总的迭代次数为24次时,算法均已收敛,对于Lorenz序列的其他加入噪声和异常点的方式以及Rossler和太阳黑子序列情况,算法收敛情况类似.

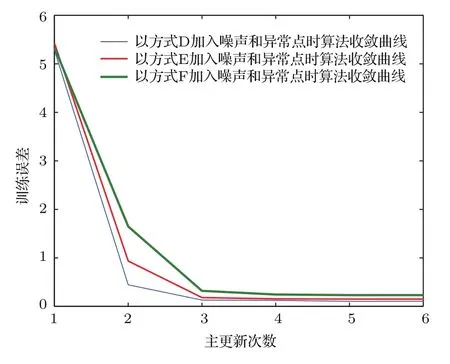
图9 以Lorenz序列为例,Robust-ELM收敛曲线Fig.9.Convergence curves of Robust-ELM for Lorenz chaotic time series.

5 结 论

本文在贝叶斯框架下提出Robust-ELM预测模型,所提模型不但具备了基于贝叶斯学习方法的模型参数自动学习能力,避免了交叉验证选取正则化参数过程,同时所提模型将混合高斯模型作为极端学习机输出似然函数,提高了模型的鲁棒性,且由于学习得到的输出权值具有稀疏性,提高了模型的泛化能力和预测精度.通过将所提模型应用于含有噪声和异常点的大气环流模型方程、Rossler混沌时间序列以及太阳黑子时间序列的预测中,证明了所提模型对于解决含有噪声和异常点的时间序列物理量预测问题,具有一定的实际应用价值.

[1]Xiu C B,Xu M 2010 Acta Phys.Sin.59 7650(in Chinese)[修春波,徐勐 2010物理学报 59 7650]

[2]Han M,Xu M L 2013 Acta Phys.Sin.62 120510(in Chinese)[韩敏,许美玲 2013物理学报62 120510]

[3]Zhang J S,Xiao X C 2000 Acta Phys.Sin.49 403(in Chinese)[张家树,肖先赐 2000物理学报 49 403]

[4]Li D C,Han M,Wang J 2012 IEEE Trans.Neural Netw.Learn.Syst.23 787

[5]Wang X Y,Han M 2015 Acta Phys.Sin.64 070504(in Chinese)[王新迎,韩敏 2015物理学报64 070504]

[6]Li R G,Zhang H L,Fan W H,Wang Y 2015 Acta Phys.Sin.64 200506(in Chinese)[李瑞国,张宏立,范文慧,王雅2015物理学报64 200506]

[7]Chandra R,Ong Y S,Goh C K 2017 Neurocomputing 243 21

[8]Politi A 2017 Phys.Rev.Lett.118 144101

[9]Ye B,Chen J,Ju C 2017 Comput.Nonlin.Scien.Num.Simul.44 284

[10]Koskela T,Lehtokangas M,Saarinen J,Kask K 1996 Proceedings of the World Congress on Neural Networks(San Diego:INNS Press)p491

[11]Jaeger H,Haas H 2004 Science 304 78

[12]Dutoit X,Schrauwen B,van Campenhout J 2009 Neurocomputing 72 1534

[13]Ma Q L,Zheng Q L,Peng H,Tan J W 2009 Acta Phys.Sin.58 1410(in Chinese)[马千里,郑启伦,彭宏,覃姜维2009物理学报58 1410]

[14]Huang G B,Zhu Q Y,Siew C K 2006 Neurocomputing 70 489

[15]Soria-Olivas E,Gomez-Sanchis J,Martin J D 2011 IEEE Trans.Neural Netw.22 505

[16]Huang G B,Wang D H,Lan Y 2011 Int.J.Mach.Learn.Cybern.2 107

[17]Han M,Xi J,Xu S 2004 IEEE Trans.Sig.Proc.52 3409

[18]Liu X,Wang L,Huang G B 2015 Neurocomputing 149 253

[19]Lu H,Du B,Liu J 2017 Memet.Comput.9 121

[20]Wang X,Han M 2015 Engin.Appl.Artif.Intell.40 28

[21]Tang J,Deng C,Huang G B 2016 IEEE Trans.Neural Netw.Learn.Syst.27 809

[22]Huang G B,Zhou H,Ding X 2012 IEEE Trans.Syst.Man Cybern.B 42 513

[23]Tipping M E,Lawrence N D 2005 Neurocomputing 69 123

[24]Tipping M E 2001 J.Mach.Learn.Res.1 211

[25]Faul A C,Tipping M E 2001 International Conference on Arti ficial Neural Networks Vienna,Austria,August 21–25,2001 p95

[26]Wang B,Titterington D M 2006 Bayes.Analys.1 625