巧解多面体内切球和外接球问题

韩晓娟

（甘肃省岷县第一中学，甘肃 定西）

多面体的内切球和外接球问题是一直困扰广大高考考生的一个难点，又是高考的热点，如何快速简单地解决这个问题呢？下面谈谈我的几点认识。

巧解一：用特殊图形体对角线求直径

1.与正方体或长方体的外接球的有关问题

题1.一个长宽高长分别为3、4、5的长方体，它的外接球的表面积为__________。

2.棱柱的外接球与内切球的问题

题2.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则球 O 的半径为_____。

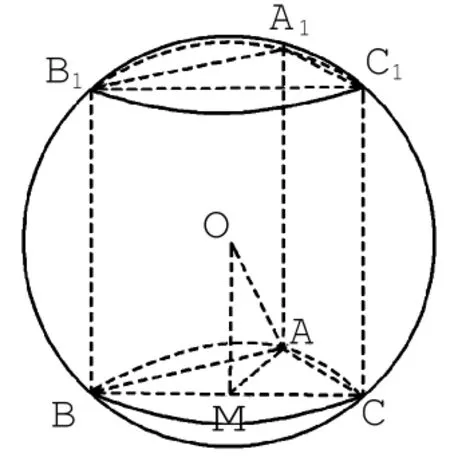
图1

解析：如图1所示，由球心作平面ABC的垂线，则垂足为BC的中点M。

3.正棱锥的外接球与内切球的问题

题3.已知棱长为a的正四面体，则此正四面体的内切球的表面积为_____________。

解析：如图2正四面体中，M为顶点P在下底面的射影，也就是底面三角形ABC的重心，

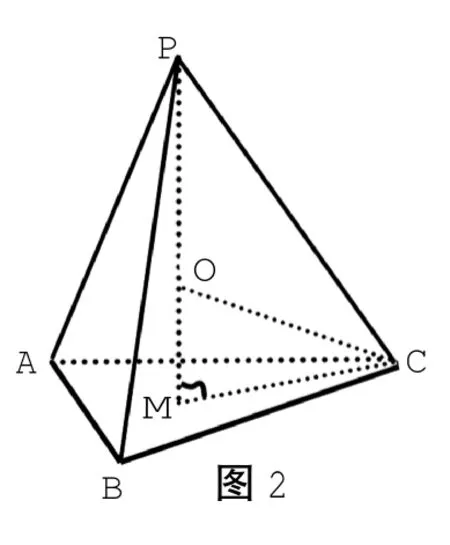
图2

题4.已知侧棱和底面边长都是3的正四棱锥，则其外接球的半径是多少？

解析：依题意，过顶点P做下底面的垂线，垂足为M,则外接球的球心在线段PM上，设为O点，连接OA,在RT△OMA中，OM=PM-R=3-R，MA=3，又OA2=OM2+MA2，解得：R=3

巧解二：补形法（出现相互垂直的“墙角”时，可补形为正方体或长方体）

巧解思路：如果在一个三棱锥中，同一顶点处有三条互相垂直的侧棱，就可以将这个三棱锥补形成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径。出现互相垂直的三条共点棱或互相垂直的三个共点面结构时用补形方法，联系长方体可将复杂的问题巧妙转化为简单问题从而轻松解决。

题5.如图3为某四棱锥的三视图，则求该四棱锥的外接球的表面积为___________

图3

解析：由三视图可得该几何体为一条侧棱垂直于下底面的四棱锥，且下底面为正方形，由此可从该棱垂足处的三条相互垂直的棱将该四棱锥补形成长方体，所以该长方体的外接球也是原四棱锥的外接球，又直径=所以半径所以外接球表面积S=

巧解三：由多面体体积和表面积利用公式求内切球半径

题6.已知某几何体的三视图如图4所示，则该几何体内切球的表面积为________________

图4

巧解思路：将一个三棱锥按内切球球心与各定点连线可分成四个等高的小三棱锥，高都为内切球的半径，而四个底则为原三棱锥四个侧面，由四个小三棱锥的体积和为大三棱锥体积，可得公式由此可直接求得内切球半径。此方法适合表面积和体积易求的三棱锥中。

相信有了这些解题思路和方法，多边形的内切球和外接球再也不是困扰大家的难题了！