一道2017年高考试题的解法探析

冯小明

（甘肃省嘉峪关市第一中学，甘肃 嘉峪关）

近年来许多省市的高考压轴题都是导数应用问题，在考查基础知识和基本方法的同时，注重考查学生综合能力，特别是对函数与方程、化归与转化、分类讨论和数形结合等数学思想的灵活运用.本文以2017年全国新课标II卷文科压轴题为例，探析利用导数解决不等式恒成立问题的方法和策略，以期为高中数学解题教学提供参考.

1.考题再现

（2017年新课标II·文21）设函数f（x）=（1-x2）ex.

（1）讨论f（x）的单调性；

（2）当x≥0时，f（x）≤ax+1，求a的取值范围.

2.标准解法

解（1）略

（2）f（x）=（1+x）（1-x）ex.

①当a≥1时，设函数h（x）=（1-x）ex，h′（x）=-xex＜0（x＞0）

因此 h（x）在［0，+∞）单调递减，而 h（0）=1，故 h（x）≤1，

所以f（x）=（x+1）h（x）≤x+1≤ax+1.

②当0＜a＜1时，设函数g（x）=ex-x-1，g′（x）=ex-1＞0（x＞0）

所以 g（x）在［0，+∞）单调递增，而 g（0）=0，故 ex≥x+1.

当时0＜x＜1，f（x）＞（1-x）（1+x）2，（1-x）（1+x）2-ax-1=x（1-a-x-x2），

综上所述，a的取值范围是［1，+∞）.

评注 标准答案采用分类讨论和举反例的方法.先利用导数研究函数的单调性，求出最值，进而研究不等式恒成立，分三种情况讨论：①a≥1；②0＜a＜1；③a≤0，其间又用了举反例的方法，这种方法过于繁杂，学生不易想到.而且这类问题根据题型不同所涉及的解法也不相同，这是高中教学的难点，即便通过训练也很难提升.

笔者通过对该问题的探析，结合学生的思维模式，给出了以下四种行之有效的解法.

3.拓展解法

解法1 分离参数法

解当x≥0时，f（x）≤ax+1，即αx≥（1-x2）ex-1（*）对∀x≥0恒成立.

①当x=0时，（*）显然恒成立，此时a∈R.

则g′（x）与h（x）同号.

而h′（x）=-xex（x2+4x+1）＜0，所以函数h（x）在（0，+∞）上单调递减，

所以 h（x）＜h（0）=0.

所以g′（x）＜0在（0，+∞）上恒成立，函数g（x）在（0，+∞）上单调递减,由洛必达法则有

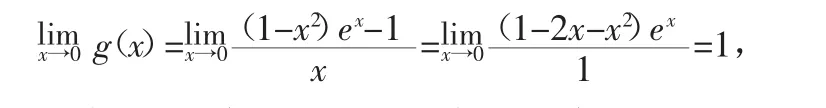
即当 x→0 时，g（x）→1，即当 x＞0 时，g（x）＜1.

因为 a≥g（x）恒成立，所以 a≥1.

因为（*）式对∀x≥0恒成立，所以由①②得a≥1.

评注 将该问题转化为学生普遍习惯采用的分离参数法，重新构造不含参的函数，再利用“洛必达法则”求解未定式的极限，该问题便迎刃而解.

解法2 二次求导法

解当x≥0时，f（x）≤ax+1，即（1-x2）ex-ax-1≤0对∀x≥0恒成立.

令g（x）=（1-x2）ex-ax-1，则g′（x）=ex（-x2-2x+1）-a

而g″（x）=ex（-x2-4x-1）＜0，即g′（x）在［0，+∞）是减函数，所以g′（x）≤g′（0）=1-a.

当 1-a≤0 时，即 a≥1 时，g′（x）≤0，此时 g（x）在［0，+∞）是减函数，

所以 g（x）≤g（0）=0，故 a≥1.

评注 构造新函数，对新函数二次求导，通过导函数的导数研究原函数的性质，不失为解决导数压轴题的良策.

解法3 数形结合法

解令g（x）=（1-x2）ex-ax-1，则g′（x）=ex（-x2-2x+1）-a.

因为g（0）=0，所以一定∃x0＞0，使得x∈［0，x0）时，g′（x）≤0，

即使得g（x）在［0，x0）单调递减，即g′（0）=a-1≤0，得a≥1.

评注 对函数进行图像分析也即数形结合，利用图像的直观性分析去解决问题，从而得到解题的思路和方法.

解法4 巧用结论法

解 由人教A版教材选修1-1第99页B组习题“利用函数的单调性，证明不等式，ex＞x+1，x≠0”，可得 ex≥x+1，将 x 代换为-x，则（1-x）ex≤1.

而f（x）=（1-x2）ex=（1+x）（1-x）ex≤x+1，又当x≥0时，f（x）≤ax+1，故 a≥1.

评注 课本是知识和方法的重要载体，也是高考命题的主要来源，本试题充分体现了“源于教材而又高于教材”的高考命题原则.

4.教学启示

高考作为选拔性考试，关注学生数学核心素养的考查，试题往往灵活多样，作为一线教师，教学时通过对一些典型试题的探析，将它转化为教学的素材，优化教学过程，提高课堂教学的时效性；同时通过典型试题从专业知识的广度和深度上拓展充实自我，从观念、理念的更新上丰富自我，不断提升自己的教学素养.