空冷汽轮发电机转子温度分布

2018-03-24 10:08王芳崔璐璐徐洪祥

哈尔滨理工大学学报 2018年1期

王芳　崔璐璐　徐洪祥

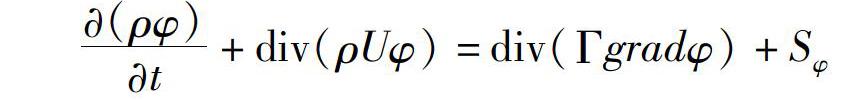
摘要：为了研究汽轮发电机转子温度分布情况，以某型空冷汽轮发电机转子为研究对象，建立三维物理模型。依据CFD原理，利用合理的基本假设和边界条件，对转子内冷却介质和固体部件的温度场进行数值求解，分析转子的温度分布。计算结果表明转子线圈温度最高达到了102℃，位于转子直线段的端部，没有超过温度限制；转子线圈整体平均温度为88.0℃，厂方试验值为87.5℃，误差为0.57%，所得结果为汽轮发电机的安全运行提供保障。

关键词：汽轮发电机；空冷；转子；温度分布

DOI：10.15938/j.jhust.2018.01.003

中图分类号： TM311

文献标志码： A

文章编号： 1007-2683（2018）01-0013-05

Abstract：In order to study the temperature distribution of the turbogenerator rotor， an aircooling turbogenerator rotor is aimed as the research object， and a threedimensional model of the rotor is established. According to the principle of CFD， basic assumptions and boundary conditions are selected， temperature field of cooling medium and solid part in rotor is solved numerically， and the temperature field distribution law of rotor is analyzed. The calculation results show that the highest temperature of the rotor winding temperature reached 102℃ which is at the end of the rotor line segment， and does not exceed the temperature limit. The wholer rotor winding draw temperature is 88.0℃ and the manufacturer test value is 87.5℃， the error is 0.57% compared with the generator for test data provided by the manufacturer， which guarantees the safe operation of turbogenerator.

Keywords：turbogenerator；aircooling；rotor；temperature distribution

0引言

随着社会发展进程的逐步加快，对电力的需求与日俱增，对空冷汽轮发电机的需求不断上升。汽轮发电机转子温升直接关系到机组的性能和经济指标，同时还影响发电机的寿命和运行的可靠性。汽轮发电机转子温升计算是汽轮发电机设计的最主要内容之一 [1-5]。

本文以某型空冷汽轮发电机转子作为研究对象，对电机转子冷却介质和各固体部件的温度场进行研究。根据CFD原理 [6-7] ，建立转子结构的物理模型和数学模型，选择合理的基本假设和边界条件，在3000r/min的穩定工况下，应用Fluent软件对转子温度场进行计算 [8] ，根据以上各计算结果，着重分析了转子内流体的温度分布规律和主要固体部件铜线圈、绝缘、槽楔的温度分布规律。考核通风系统的散热能力，保证机组安全可靠运行。

1通风系统和物理模型

转子采用轴径向通风，冷空气在发电机高压风扇加压后进入到转子端部线圈下的气室，分成两个风路，一路进入副槽，冷却空气在副槽流动的过程中在流进转子各个径向风道，最后进入气隙；另一路在转子端部线棒的轴向进风口和端部进风口进入转子线圈内部风道，其中一部分沿着轴向线圈内部风道流动进入转子径向风道，一部分沿着线圈内部风道流向转子曲段，最后经转子端部线圈下部的风道进入气隙。

该汽轮发电机转子有32个槽，沿周向对称分布分为四组，每一组放置编号为1～8的8个不同的转子线圈。由于电机左右对称，选取风阻最大，冷却效果不好的8号转子槽的一半作为三维物理模型和分析对象。转子温度场计算模型如图1所示。

图1温度场求解物理模型

2数学模型

电机内的流体视为不可压缩流体，流体的流动处于湍流状态。流动要受到质量守恒定律、动量守恒定律和能量守恒定律三大定律的制约，湍流控制方程采用k-ε两方程模型 [9-10] 。

（ρφ）t+div（ρUφ）=div（Γgradφ）+Sφ

式中：φ为通用变量，可以代表u、v、w、T等求解变量；Γ为广义扩散系数；Sφ为广义源项。

3基本假设和边界条件

3.1基本假设

1）忽略重力和浮力对流体的影响；

2）转子内流体为定常流动状态；

3）转子内流体作为不可压缩流体处理；

4）流体的雷诺数很大，采用湍流模型求解；

5）线圈主绝缘、层间绝缘各自的材料物性均相同；

6）电机内各固体部件之间完全接触，热源密度按照损耗平均分布考虑。

3.2边界条件

1）材料物性参数为常数，其中匝间绝缘材料、铜绕组、槽楔、转子铁心、护环的热导率λ数值分别为0.3、387.6、202.4、31.8、44，单位均为W/（m·K）；

2）风扇的入口表压为5000Pa，入口空气温度50℃。由于冷却空气在转子内部的平均温度接近65℃，所以定义此温度下空气物性，65℃时空气密度密度ρ=1.045kg/m3，定压比热cp=1007J/（kg·K），热导率λ=0.0293W/（m·K），动力粘度η=2.03×10-5kg/（m·s）；

3）根据厂方提供的发电机损耗数据，经过计算得到转子铜热源强度为q=284927W/m3，转子铁心热源强度为q=65137W/m3；

4）方程组采用分离、隐式求解，针对旋转流动，转速为3000r/min，旋转方向为汽端逆时针，压力速度耦合选用SIMPLEC算法，方程离散采用二阶迎风格式。

4求解结果及分析

4.1转子内流体温度分布特性

空气经过高压风扇的加压后进入到汽轮发电机的内部，与发电机内部发热部件进行热量交换，冷却介质温度分布直接影响着发热部件的温度分布。所建立的8号转子槽模型共有25个完整径向风沟和一个半个风沟，分别对径向风沟进行编号为1～26号，1～3号径向风沟内的空气是流自12个转子轴向风沟，4～26号径向风沟的冷空气是来自副槽。

图2为转子径向风道及副槽温度分布。空气最低温度为51.7℃，最高温度为102℃。冷空气入口温度为50℃，冷空气在流经转子端部气室进入副槽的过程中，被转子最下层的端部线圈和曲段线圈加热，因此在到达副槽入口时，温度略有升高，副槽内的空气在沿轴向运动的过程中不断的被两侧的转子铁心和垫条加热，在到达副槽尽头时，槽内的空气温度已经升高到68.6℃。从4、12、19、24号径向風道放大图可以看出进入径向风道内的空气温度也在不断的升高，同时因为副槽内空气流速的降低，使得涡旋的范围逐渐的减小，径向风道内空气的温度分布更加均匀；1～3号转子径向风道内的空气是流自12个轴向进风口，冷空气从高压风扇流入到轴向进风口的过程中会有摩擦生热和被一些发热部件的加热，所以1～3号径向通风道内空气的温度要高于4～26号，

最高温度102 ℃出现在2号径向通风道内。

图3显示的是轴向通风段的空气温度分布，1～3号转子径向风道内的空气是流自12个轴向进风口，冷空气从高压风扇流入到轴向进风口的过程中会有摩擦生热，也会被一些发热部件加热，致使进入轴向进风口的最低空气温度达到了52.4℃；如图 4是12个轴向进风口平均温度分布，从温度分布上看，进口温度是先升高，再降低，在12轴向进风口所处气室由于电机结构和空气流速的因素形成了一个涡旋，涡旋的产生使得空气不能及时的进入风道而滞留在涡旋中，使得整体的空气进入量降低，因此涡旋中心区空气温度高，沿着半径的增大，温度逐渐降低，4号和5号轴向进风口正处于涡旋中心附近，因此进口空气温度最高达到了63℃左右。

图5为转子曲段风道内空气温度分布。冷空气在风道内运动的过程中不断的与线圈发生热交换使得空气的温度不断的升高，由于线圈处于转子端部，距离风扇入口很近，转子端部风室的空气温度都很低，因此对端部线圈冷却的效果比较好；线圈的冷却主要靠风道内的空气冷却，冷却效果不好，线圈的冷却主要靠风道内的空气冷却，因此线圈的温度较高，线圈内的空气温度也随之升高，空气的最高温度为99.6℃，处于转子曲段的端部。

图6是转子端部风室的温度分布，由于距离风扇入口很近，空气的最低温度和入口的边界条件接近为50.1℃，最高温度在端部出风口附近的气室内为97.0℃；轴向进风口和端部进风口所在部分的风区产生了两个旋转方向相同的涡旋，涡旋中心的域因为流动不畅，形成了一个高温区达到了72.5℃，明显高于涡旋外围的空气温度，12个轴向进风口纵向排列正好贯穿这个涡流，12个端部进风口纵向排列处于涡旋的边缘，因此轴向进风口进风温度没有端部进风口进风温度相对均匀；气室的其余空气流通不好的地方温度也比较高；端部出风口所处的气室与风扇后的气室不相同，内部产生的热量主要靠转子线圈内的冷空气换热带走，因此整体的温度较高，气室内的最高温度也是在这里。外部冷却气室内的空气没有轴向进风口和端部进风口所在气室流动状态好，处于这部分空气与转子固体部分的相对流速低，因此转子线圈产生的热量不能被及时的传递出去，处于外部冷却气室的转子线圈温度较高，同时也把与之接触的空气温度加热到比较高。

4.2转子内主要固体部件温度分布特性

汽轮发电机转子发热部件主要有线圈和铁心，其他主要结构如槽楔、绝缘是不发热的，但是受到发热部件的影响，它们也有一定程度温度的升高，温升会直接影响发电机内部各个部件的机械性能。

转子线圈是发电机内温升较高的部件，该汽轮发电机转子每个槽有12层转子线圈，每层线圈之间有绝缘分隔，如图7为模型转子线圈温度分布。

转子曲段线圈与冷空气接触的壁面导热良好，同时线圈内部还有从端部进风口流入的低温空气，在内外双重散热的情况下，转子曲段线圈的整体温度比较低，在80℃左右；转子端部最上层与护环接触，护环本身并不发热，温度较低，因此线圈的热量传导给护环，温度进一步降低，最低达到了58.4℃；端部出风口附近的线圈所处的气室与风扇后气室并不相通，气室内的空气是从端部出风口流出的空气，温度较高，线圈温度升高达到了99.6℃；转子线圈最高温度为102℃，在转子直线段的端部，即1～3号径向风道处，冷空气从轴向进风口流入到线圈内部风道，由于形成了涡旋，致使进入12个线圈内的空气流量不均匀，空气量变少，经过轴向线圈的加热，使得进入1～3号径向风道时空气温度比较高，线圈的升温幅度明显高于其他部分的线圈；4～26号径向风道内冷空气是来自副槽，空气的温度较低，一般在93.2～97.6℃之间；转子线圈整体的平均温度为88.0℃，工厂试验值为87.5℃，误差为0.57%，说明模拟计算结果是比较准确的。

在发电机等电气设备中，绝缘材料是最为薄弱的环节。绝缘材料尤其容易受到高温的影响而加速老化并损坏。本模型的发电机采用是F级绝缘等级，允许的工作温度为155℃，图8是转子绝缘温度分布，温度最低为51.9℃，位置在下侧轴向经风口，此处与进入线棒内的冷空气直接接触进行热量交换，因此此处绝缘的温度与冷空气的温度是相同的；绝缘的最高温度也出现在1～3号转子径向风道附近，达到了102℃，没有超过F级绝缘允许工作的范围；曲段线圈的最高温度出现在端部出风口附近，温度达到98.8℃；径向风道附近的绝缘由于直接受到空气的冷却，温度略低，范围在76.8～81.8℃，中间部分绝缘的温度较高，转子绝缘整体的平均温度为87.4℃。

图9是转子槽楔温度分布，槽楔位于转子垫条上面，直接接触气隙，槽楔本身并没有损耗的产生，热量的来源主要是垫条和转子铁心，槽楔的材料是铝，导热系数相对较好，因此它的温度分布受气隙内冷空气温度分布影响很大，从图9中可以看出槽楔的温度分布在径向方向上没有什么梯度变化，而在轴向方向上梯度分布很明显，最高温度出现在槽楔的端部达到了84.4℃，槽楔整体的平均温度为80.8℃[11]。

5结论

1）转子径向风道内流体的温升趋于均匀，1～3号转子径向风道内空气温度较高，最高温度102℃出现在2号径向通风道内。

2）转子曲段线圈的整体温度比较低，在80℃左右；端部出风口附近的线圈温度较高，达到了99.6℃；转子线圈最高温度为102℃，在转子直线段的端部；线圈整体的平均温度为88.0℃，工厂试验值为87.5℃，误差为0.57%，模拟计算结果较准确。

3）绝缘的最高温度为120℃，绝缘采用F级绝缘，工作温度为155℃以下，因此绝缘没有超温。

参考文献：

[1]李和明，李俊卿.电机中温度场计算方法及其应用[J].华北电力大學学报，2005，32（1）：1-5.

[2]路义萍，大型空冷汽轮发电机转子流场与温度场数值模拟[D].哈尔滨：哈尔滨理工大学，2007，26（2）：5-17.

[3]李伟力，项欢.汽轮发电机径切两向空冷系统转子温度场的计算[J].大电机技术，1998（2）：15-18.

[4]高斯博.水氢氢冷却汽轮发电机热流场分析[D].哈尔滨：哈尔滨理工大学，2015：10-15.

[5]路义萍，洪光宇，汤璐，等.多风路大型空冷汽轮发电机三维流场计算[J].中国电机工程学报，2013，33（3）：133-136.

[6]牛莲静.大型发电机定子流场及温度场数值计算与分析[D].哈尔滨：哈尔滨理工大学，2013：41-50.

[7]王芳，郭瑞倩，安志华，等.空冷发电机定子三维温度场分布与试验对比[J].电机与控制学报，2013，17（12）：46-50.