间歇采样延时叠加干扰效能研究
刘 俊,刘 建,苏保禹,吴明宇
(中国航天科工集团8511研究所,江苏 南京 210007)
0 引言
雷达系统为了满足提高探测距离和距离分辨率的双重要求,要求采用大时宽带宽积信号[1]。通常雷达信号的大时宽带宽积性能是通过信号的非线性相位调制获得的,如脉宽内线性调频、非线性调频、频率编码和相位编码等。通过对这类信号进行脉冲压缩处理能够利用其脉内的相干性获得较高的处理增益,使得与雷达发射波形不匹配的干扰信号无法获得相应处理增益,从而大大提高了雷达的抗干扰性能。针对这一问题,国内外众多学者对脉冲压缩体制雷达的干扰方式进行了大量的研究[2-10]。
脉冲压缩雷达的抗干扰性能本质是由于干扰信号与雷达信号不相干,无法获取雷达的脉压处理增益所形成的。因此只要能保证干扰信号与雷达信号的相干性就能够对脉压雷达产生干扰。文献[2]中基于DRFM采用的全脉冲复制转发的干扰方式,能够获取雷达的脉压处理增益,形成有效的假目标欺骗干扰。然而这种干扰方式形成的假目标至少滞后雷达回波一个脉冲宽度,会使干扰机搭载平台暴露在对方的雷达视野中,这对于某些重要作战搭载平台而言是无法接受的。针对脉压雷达中最常见的线性调频信号,文献[3]基于干扰机的收发分时机制提出了间歇采样干扰,该干扰方式可以产生相干假目标串的干扰效果,既解决了干扰信号不能获取雷达脉冲压缩处理增益的问题,又能够对干扰机搭载平台形成有效的掩护效果。但是该干扰方式只能在目标附近形成假目标,无法对干扰搭载平台后方目标产生掩护的干扰效果。
本文针对线性调频信号,提出了间歇采样延时叠加干扰(以下简称为延时叠加干扰)方法。通过理论推导和仿真分析验证,该干扰能够通过雷达的脉冲压缩处理在干扰搭载平台附近及后方形成密集的相干假目标,取得对干扰搭载平台本身以及后方目标进行掩护的干扰效果。此外本文对线性调频信号使用延时叠加干扰可能产生的相消现象进行了研究,给出了2种不同的解决方法,并通过仿真验证了所提方法的有效性。
1 间歇采样干扰原理
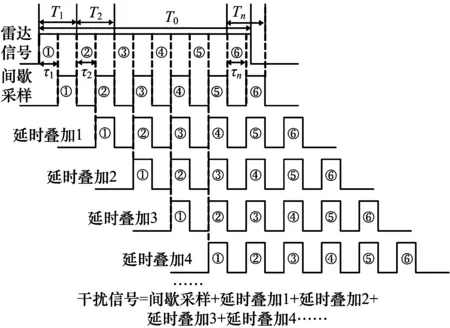
间歇采样干扰是一种基于干扰机收发分时体制,通过利用雷达对回波信号的脉冲压缩处理特性,产生相干假目标串的干扰样式,其干扰时序图如图1所示,其中T0为雷达信号脉冲宽度,T1是间歇采样周期,τ是接收时间窗。下面将以线性调频雷达信号为例,对间歇采样干扰的数学原理进行公式推导。
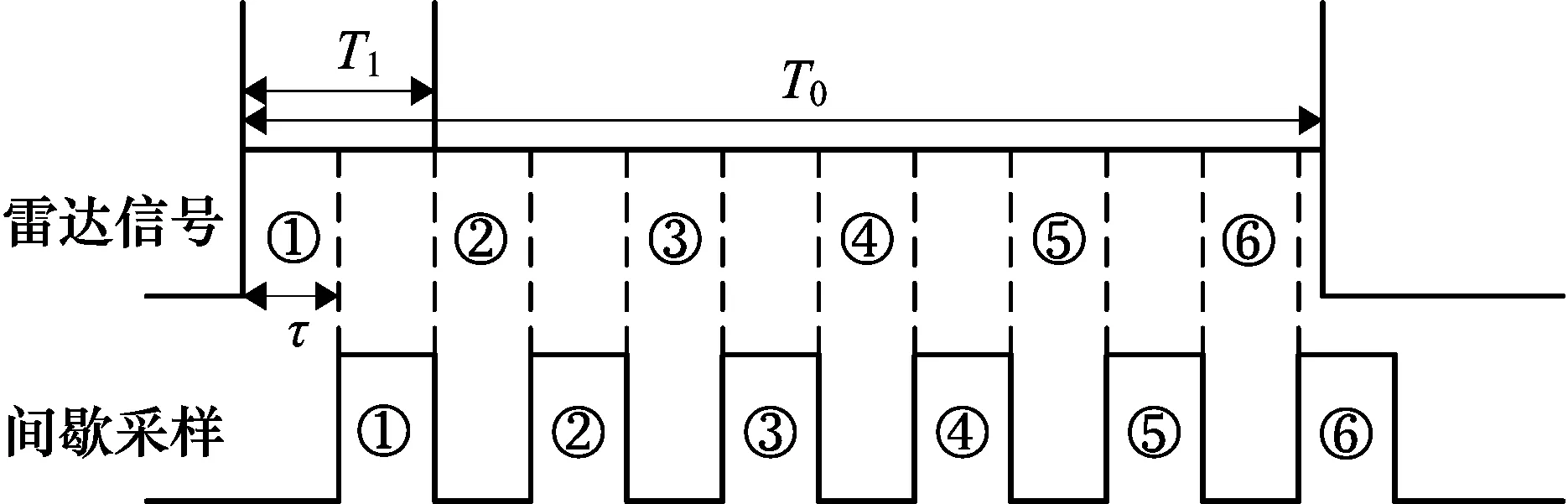
图1 间歇采样干扰时序
假设雷达的发射信号为:
s(t)=rectt/T0expjπKt2
(1)
式中,rect(t/T0)=1,|t|≤T0/2,K=B/T0为调频斜率,B为调频带宽。
假设u(t)是一个脉宽为τ,周期为T1的矩形包络脉冲串信号,如图2所示。表达式为:
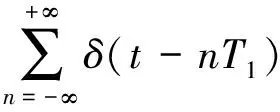
(2)
式中,*表示卷积运算,δ(·)表示狄拉克函数,n为整数。
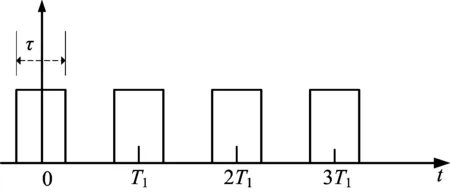
图2 矩形包络信号
那么间歇采样干扰回波信号可以表示为:
j0(t)=s(t)u(t)
(3)
对于周期性的脉冲串波形,用傅里叶级数展开:
(4)
式中,f1=1/T1是间歇采样重频。
代入式(3),得:
(5)
式中,sn(t) =s(t)e2πnf1 t,an=(τ/T1)Sa(nπf1τ),Sa(x)=sinx/x。
由式(5)可知:周期性间歇采样相当于对原信号进行了一系列的多普勒移频调制和幅度加权,移频大小即为脉冲串u(t)的各次谐波频率。
令匹配滤波器冲击响应h(t)=s*(-t),其中(·)*表示取共轭。
则目标回波信号通过匹配滤波的响应为[1]:
y(t)=s(t)*s*(-t)
=χ(τ,ξ)|τ=t,ξ=0
=(T0-|τ|)Sa(π(Kτ-ξ)(T0-|τ|))·
e-jπξτ|τ=t,ξ=0
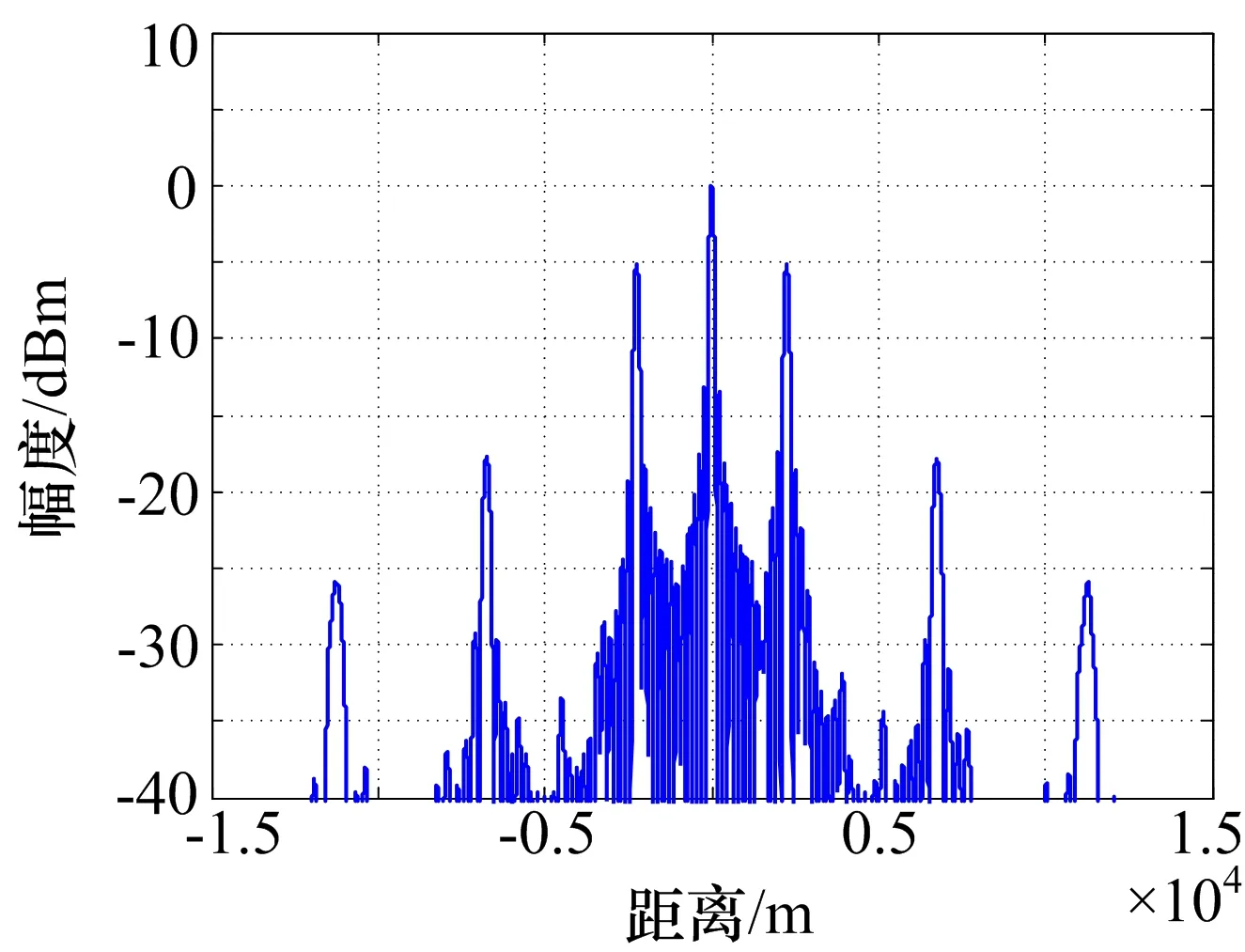
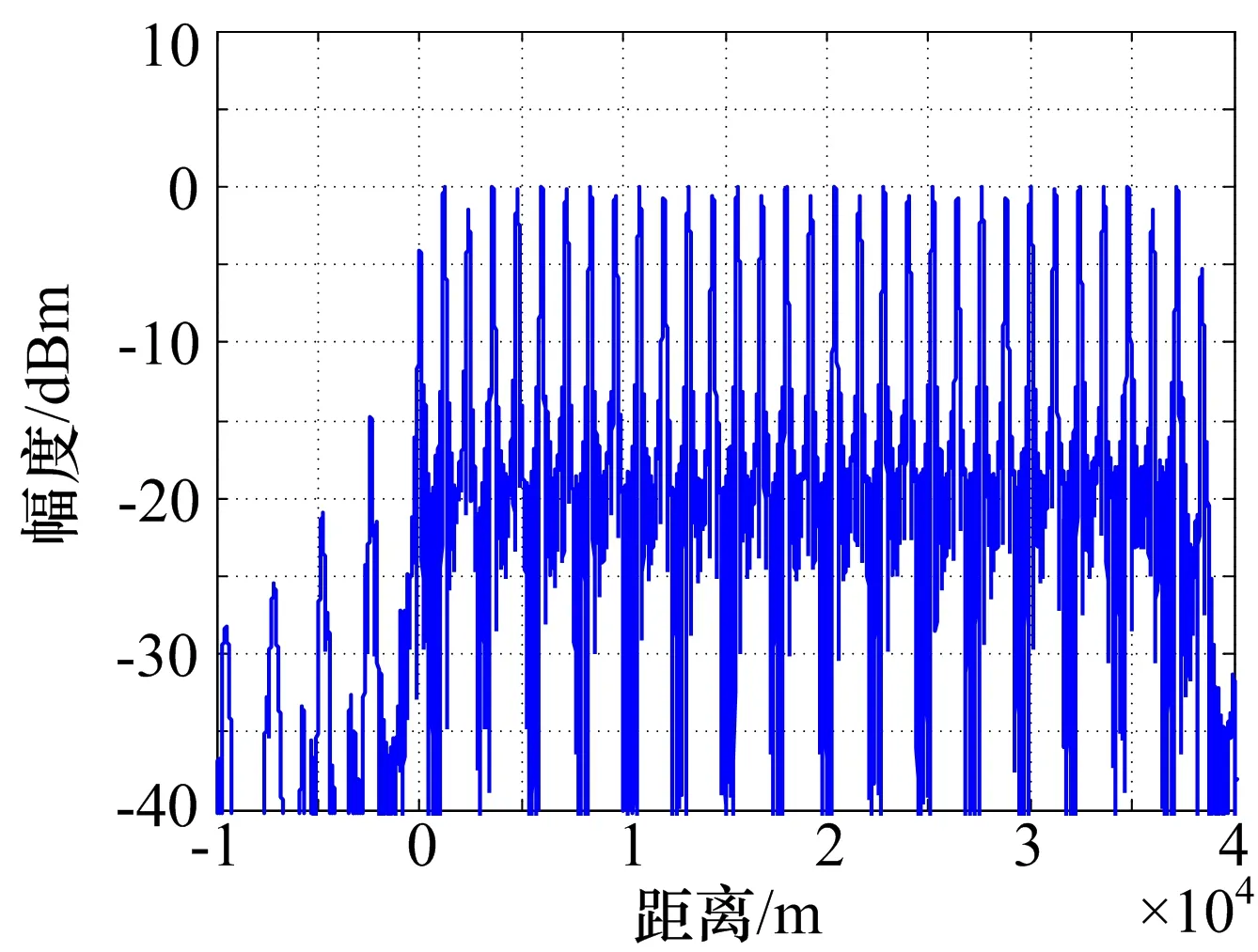
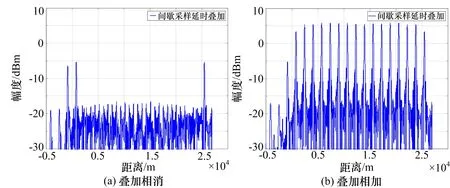
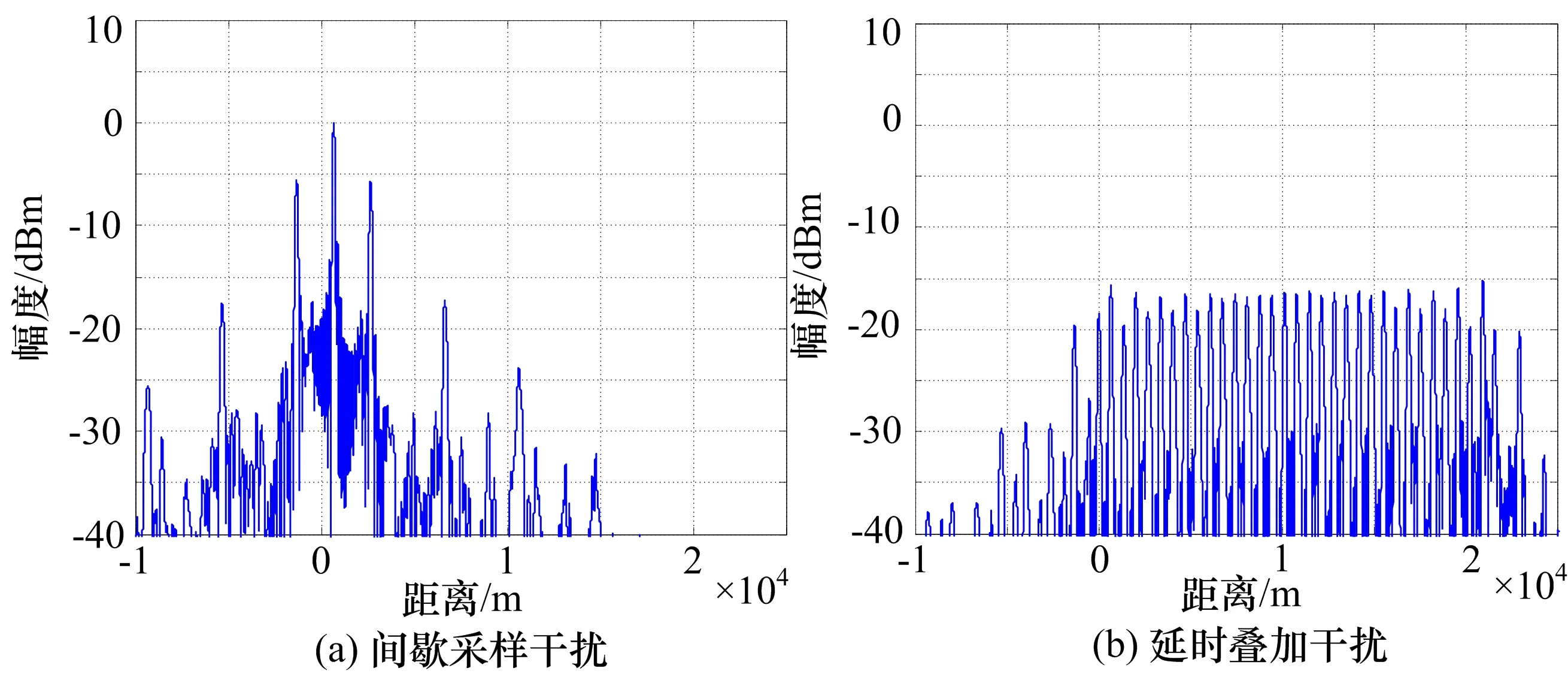
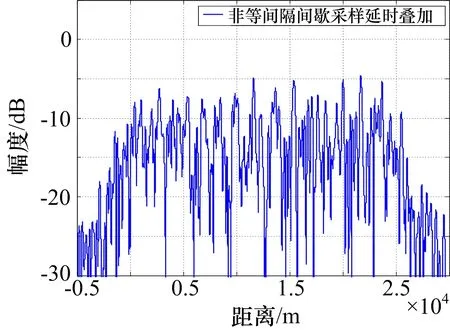
=(T0-|t|)Sa(πKt(T0-|t|)),|t| (6) 于是,对于n次谐波移频调制信号sn(t) =s(t)·e2πnf1 t,匹配滤波输出: yn(t)=sn(t)*h(t)=χ(τ,ξ)|τ=t,ξ= -nf1 =(T0-|t|)Sa(π(Kt+nf1)(T0-|t|))· ejπnf1t,|t| (7) 根据以上公式,yn(t)的峰值在t=-nf1/K处取得,即线性调频回波信号的频移干扰将会导致脉压输出在延时上出现偏移,且延时偏移量与频移量关系为:Td=fd/K[11],其中Td、fd分别为延时偏移量和频移量。 间歇采样干扰回波信号经过脉冲压缩处理的输出为p0(t)=j0(t)*h(t),即: (8) 由式(7)可以得到,p0(t)各个峰值位置出现在t=-nf1/K附近。由式(8)可以得到,p0(t)各个峰值的幅度由|anyn(t)|决定。 假定T1=2τ,则p0(t)各峰值点取值为: anyn(-nf1/K)=(sin(nπ/2)/(nπ)(T0- |nf1/K|) (9) 由于|t| |anyn(-nf1/K)|=sin(nπ/2)/(nπ)(T0- |nf1/K|) (10) 当n=0时,|anyn(-nf1/K)|=0.5T0;当n为非零偶数时,|anyn(-nf1/K)|=0;n为奇数时,|anyn·(-nf1/K)|=T0/(|n|π-f1/(Kπ),即随着|n|的取值不断增大,p0(t)各个峰值的幅度随|n|增大近似按1/|n|衰减。图3是|anyn(-nf1/K)|的归一化幅度变化曲线,从图中可以看出,当n≥2,|anyn(-nf1/K)|的取值衰减量超过10 dB。所以,通常干扰性能分析时忽略p0(t)中二次以上的谐波分量。 图3 幅度变化曲线 综上所述:1)p0(t)在t=0处幅值最大,形成了主假目标;2)p0(t)在t=±1/(KT1)处取极大值,形成相干假目标,通常把这2个极大值点称为左右次假目标,如图4所示。因此,间歇采样干扰能够在目标回波附近形成3个幅值较高的假目标。 图4 间歇采样干扰效果图 由于间歇采样在目标附近形成的假目标个数少,且假目标只能出现在靠近目标回波处,无法对干扰机搭载平台身后的目标形成有效的掩护干扰效果。本文提出的延时叠加干扰能够在干扰搭载平台身后形成大范围密集假目标,能够对身后目标形成有效的掩护式干扰效果。 延时叠加干扰是基于间歇采样干扰提出的一种干扰样式,该干扰样式在时序上的产生方式就是在不打断正常的间歇采样的基础上将间歇采样的信号延时到下一个收发周期叠加输出。图5是基于接收发射窗1∶1的间歇采样,描绘了延时叠加干扰的干扰时序。 从图5中可以看出,延时叠加干扰可以看作是间歇采样干扰周期性延时叠加产生的。因此延时叠加回波信号可以表示为: (11) 式中,N为总叠加次数,i为非负整数。 图5 延时叠加干扰时序 从而延时叠加干扰的回波信号经过脉冲压缩处理的输出为: (12) 由式(12)可以很容易发现,延时叠加干扰的回波信号经过脉冲压缩处理的输出就是由具有不同延时的间歇采样信号通过脉冲压缩处理后矢量相加得到的,因此延时叠加干扰信号被雷达接收后通过脉冲压缩处理可以在目标附近及后方形成N个主假目标和2N个次假目标(每个主假目标在时间距离上相隔T1),在目标附近及后方产生密集相干假目标群,其效果图如图6所示。 图6 延时叠加干扰效果图 图7 主假目标与次假目标重叠 延时叠加干扰产生了大量的假目标,但在特定情况下有可能出现干扰幅度相消或相加的情况。如果参数设置不当往往达不到预期干扰效果,具体分析如下: iT1+τ=qT1+τ-1/KT1 (13) 由式(13)可以求出,T1=(T0/(B|q-i|))1/2。等式两边同时加上iT1并移项可以得到(2i-q)T1+τ+1/(KT1)=iT1+τ,即w2i-q(t)的次假目标也与wi(t)的主假目标位置重合。 令t0=iT1+τ,T1=(T0/(B|q-i|))1/2,则: p(t0)≈w2i-q(t0)+wi(t0)+wq(t0) =p0(t0-(2i-q)T1-τ)+ p0(t0-iT1-τ)+p0(t0-qT1-τ) ≈Saπτ/T12τT0-1/KT1/T1· (14) 综上所述,雷达采用线性调频信号时,当延时叠加干扰形成的主假目标与次假目标重合,即T1=(T0/(|i-q|B))1/2时,会出现幅度相消或相加的现象,如图7所示。 由上述分析可知,对于线性调频信号,当雷达参数固定时,主次假目标重合现象只会出现在采用某些特定收发周期的延时叠加干扰中。而作战环境中很难提前获知敌方雷达的相关脉宽及带宽信息,只能通过改变延时叠加干扰的收发周期减小上述现象对干扰效果的影响。为此提出了2种改进方法。 1)改进方法一:脉组间间歇采样周期参差,即每间隔一定时间改变间歇采样周期。 2)改进方法二:脉内间歇采样周期参差,即在同一个雷达发射脉宽内采用不同的间歇采样周期,如图8所示,其中T0≠T1≠…≠Tn。从而避免了由于设定的某个间歇采样周期使p(t)几乎所有主假目标与次假目标重合,导致整体幅度减小。 图8 不等间隔叠加干扰时序 仿真条件:脉宽120μs,带宽1MHz,采样频率100MHz,接收时间τ=4μs,间歇采样周期T1=8μs。 图9 干扰效能对比 图9(a)是间歇采样干扰脉压后形成的干扰效果图,纵轴是已经幅度归一化的幅度。图9(b)是延时叠加总次数N=16的延时叠加干扰脉压后形成的干扰效果图,纵轴是以图9(a)中最大幅值进行归一化的幅度。对比图9(a)、(b)可以发现,延时叠加干扰将干扰信号能量均匀分布在干扰搭载平台后方,可以对20km左右的范围形成掩护的干扰效果,远大于间歇采样干扰的干扰范围。 仿真条件:脉宽120μs,带宽1MHz,采样频率100MHz,接收时间τ∈[4,8]μs,间歇采样周期T1=2τ,延时叠加16次。 表1是采用改进方法一的延时叠加干扰经过10000次蒙特卡洛试验得到的数据。统计的是信号p(t)在间歇采样周期随机变化中出现幅度相消的次数。从试验数据得出,出现幅值相消概率为4.77%。这就意味着,当雷达参数固定时,即使没有雷达参数先验信息,也只有4.77%的概率出现叠加相消现象,且由于间歇采样周期的随机性,下一次再出现相消现象的概率只有0.23%。说明采用改进方法一的延时叠加干扰,可以大大降低由于叠加相消被雷达发现的概率,且即使被发现一次也会由于收发周期的随机变换无法建立航迹。因此,可以通过脉组间间歇采样周期参差的方式,减小延时叠加干扰出现叠加相消所带来的影响。 表1 相消统计表 仿真条件:脉宽120μs,带宽1MHz,采样频率100MHz,接收时间τ∈[4,6]μs按照正态分布随机选取,间歇采样周期T1=2τ,延时叠加16次。 图10是改进方法二形成的干扰效果图,从中可以看出信号的整体幅度虽然有所下降,但是并没有形成幅度下陷凹坑,相比于图7(a)的相消现象有显著的改善,并且这种非等间隔采样能够形成更加密集的假目标。 综上所述,本文提出的延时叠加干扰能够有效增大干扰范围,且提出的2种改进方法能够降低该干扰可能出现的叠加相消现象。 图10 改进方法二仿真 本文以线性调频信号为背景,在间歇采样的基础上,提出了延时叠加干扰方法,该干扰信号经过雷达的脉冲压缩处理后,能够在干扰搭载平台附近及身后形成大范围的密集假目标,得到掩护式干扰效果。此外,本文对延时叠加干扰存在的叠加相消问题进行了分析,提出了2种改进方法,并通过MATLAB仿真验证了所提方法的有效性。■ [1] 陈伯孝,等.现代雷达系统分析与设计[M]. 西安:西安电子科技大学出版社,2012:177-218. [2] 王跃鹏,黄建冲.基于DRFM的雷达综合欺骗干扰[J].电子对抗,2005(5):1-5. [3] 王雪松,刘建成.间歇采样转发干扰的数学原理[J].中国科学,2006,36(8):891-901. [4] 刘忠,王雪松.基于数字射频存储器的间歇采样重复转发干扰[J].兵工学报,2008,29(4):405-410. [5] 刘巧玲,李文成,张文明,等.间歇采样移频转发干扰效果仿真分析[J].电子信息对抗技术,2009,24(1):48-50,65. [6] 郭雷,李宏,李青山. 相参雷达间歇采样灵巧干扰方法[J].现代防御技术,2013,41(3):111-116. [7] 张鹏程,王杰贵.基于DRFM的间歇采样预测转发干扰分析[J]. 系统工程与电子技术,2015,37(4):795-801. [8] 张养瑞,李云杰,李曼玲,等. 间歇采样非均匀重复转发实现多假目标压制干扰[J]. 电子学报,2016,44(1):46-53. [9] 杨少奇,田波,周瑞钊. 利用时频分析的间歇采样干扰对抗方法[J].信号处理,2016,10(32):1244-1251. [10] 李文臣,黄烽,杨会民,等.雷达噪声干扰和多假目标干扰效能分析[J].中国电子科学研究院学报,2013,4(8):403-406. [11] 王雪松,肖顺平,冯德军,等. 现代雷达电子战系统建模与仿真[M]. 北京:电子工业出版社,2010:139-159.

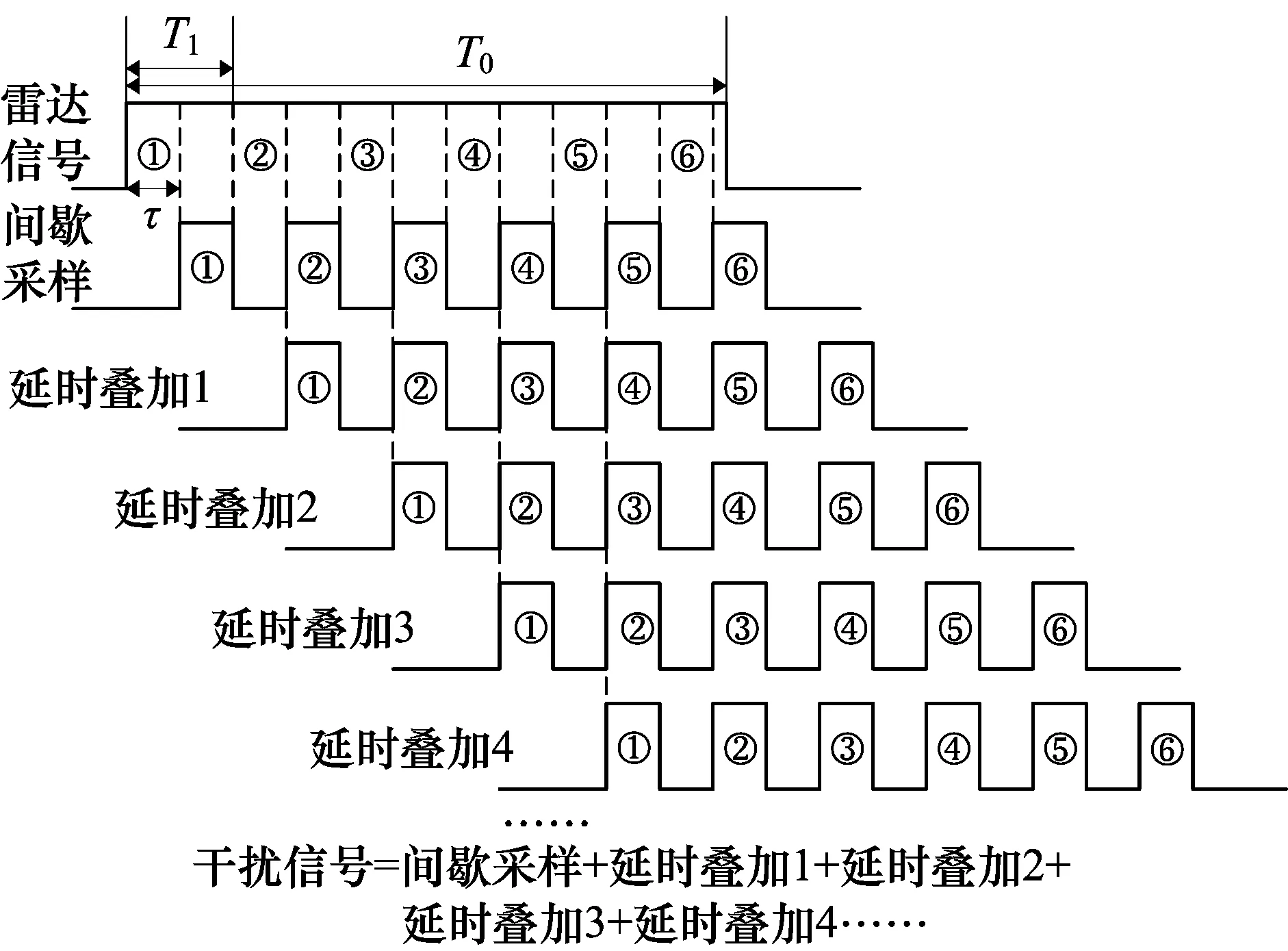
2 延时叠加干扰原理
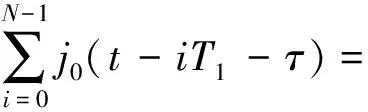
3 相消现象及解决方法
3.1 相消现象
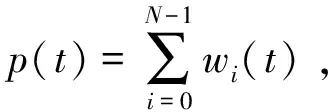
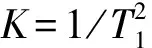
3.2 解决方法
4 仿真分析
4.1 延时叠加干扰效果仿真
4.2 脉组间间歇采样周期参差仿真

4.3 脉内间歇采样周期参差仿真
5 结束语

