P2P网络借贷系统演化过程研究

周春来 刘峰涛

【摘要】本文基于自组织理论和他组织理论对P2P网络借贷系统的自组织演化和复合演化过程进行了定性分析，并基于第一网贷的交易数据利用近似熵以及样本熵算法对其复合演化过程进行了定量描述。研究发现P2P网络借贷系统演化过程中，自组织演化起主导作用，政策监管、行业规范等他组织起辅助作用，有效的他组织能够降低或加速降低P2P网络借贷系统的无序程度；近似熵与样本熵算法能够对P2P网络借贷系统的有序度进行测度，并在数据序列长度达到300个以后，两者具有较高的稳定性；政策监管、行业规范等他组织作用的反应周期一般为两个月，过多的监管与规范并不能带来P2P网络借贷系统有序性的提高。

【关键词】P2P网络借贷系统 自组织 复合演化过程 近似熵算法 样本熵算法

一、背景

P2P网络借贷作为一种新型的投融资模式，不仅受到中小微企业青睐，也是个人投资者投资理财的新选择。截至2016底，网贷行业累计平台数量达到5877家，全年成交量20636亿元，远超2015年全年网贷行业9823亿元的成交量，但累计停业及问题平台数达到3429家，跑路、提现困难等问题层出不穷。一边是迅猛发展势头不减，一边是问题平台不断，毁誉参半的P2P网络借贷受到了越来越多理论界与实务届的关注，国内外对其展开了多角度的研究。不管是对平台融资效率还是对借贷双方借贷行为，学界都展开了相当多的研究。然而，P2P网络借贷系统作为复杂经济系统，其演化发展不仅涉及自身自组织的发展，同时还不可避免的受到外部他组织如政府、行业协会等多方因素的影响，已有的研究仅局限于关注系统某一方面的影响因素的研究，缺乏对系统整体性演化机理与演化过程的研究。系统整体性研究的缺乏使得监管等的实施效果不佳。本文基于自组织理论与他组织理论，对P2P网络借贷系统的自组织演化于复合演化过程进行了探讨，并利用近似熵与样本熵算法对系统的复杂性进行了测度，并做了相关分析。

二、P2P网络借贷系统自组织演化与复合演化过程理论分析

自组织理论是上世纪60年代末兴起的研究系统演化的较为成熟的方法，它研究复杂系统的形成与演变机制问题，即在一定条件下，系统是如何自动地从无序走向有序、从低级有序走向高级有序的。自组织理论强调系统进行自组织演化的前提条件是具备耗散结构，动力机制是协同学。研究发现，P2P网络借贷系统具备耗散结构特征和协同学机制。耗散结构特征表现在P2P网络借贷系统具有明显的开放性、远离平衡态、存在非线性作用以及通过涨落达到有序。协同学主要体现在借贷双方当事人之间的竞争与协同、借贷平台之间的竞争与协同，而信用机制是P2P网络借贷系统中的序参量。

自组织是P2P网络借贷系统发展演化的固有本质规律，他组织是一种建立在对P2P系统固有发展演化规律认识基础上的显性干预行为，在系统复杂度不断提高、自组织力弱有效情况下，他组织显得更为明显和重要。P2P网络借贷系统中他组织行为主要体现为政策监管、行业规范，他们与P2P网络借贷系统发展演化过程当中自组织行为结合，发挥两者复合作用，共同推动P2P网络借贷系统的发展演化。在这个复合过程中，监管、自律规范与P2P网络借贷系统自组织行为处于分向的可耦合状态，监管通过调试和修正P2P网络借贷中的风险点，不断加强行业信用风险识别能力与信用风险防范意识，促使平台回归中介属性等等，推动P2P网络借贷系统不断提升自身有序程度，不断从无序走向有序，从低级有序走向高级有序。

三、基于近似熵与样本熵算法的系统有序度测度模型构建

在P2P网络借贷系统的自组织与他组织复合演化中，自组织力与他组织力是一种耦合关系，目标是通过相互作用降低系统的无序程度，提升系统的有序度。对于系统有序性的描述，克劳修斯和普利高斯等人提出熵的概念，认为熵值越大，系统越无序。熵对于系统演化的定性描述具有重要作用，但克劳修斯的平衡系统熵理论以及普利高津的非平衡开放系统的推广熵理论都无法完成对系统有序程度的定量描述。为了解决这一难题，平卡斯（Pincus）定义了近似熵（Approximate Entropy，简记为ApEn），后来学者们在近似熵基础上又发展了样本熵，用以定量描述系统有序程度。虽有两者不尽完美，但对于系统有序性的定量描述依然意义重大，因此本文使用近似熵与样本熵两种方法探讨P2P网络借贷系统的有序性，以此研究其复合演化过程。

ApEn是用一个非负数来表示前一数据对后一数据的可预测性，以定量描述时间序列的可重复性。熵值越大，表明时间序列越具有随机性或不规则性，其非周期性越强，复杂度越高；熵值越小，表明数据周期性越强，复杂度越小。

对于给定的N点时间序列{y（i）}，设定模式为数m和相似容限r，重构m维向量Y（i）。

■

对每一个i值计算向量Y（i）与其余向量Y（j）之间的距离，定义向量Y（i）和Y（j）之间的距离为两个向量对应元素中差的绝对值的最大值，即：

■

给定阈值r（r>0），对每一个i值统计d[Y（i），Y（j）]≤（r*SD）的数目，并求出统计结果与向量距离总数（N-m+1）的比值，其中SD为原始时间序列{y（i）}的标准差，记作Cmi（r）即：

■

粗略地讲，Cmi（r）反映序列中m维模式在相似容限r的意义下相互近似的概率，再将Cmi（r）取对數，求其对所有i的平均值，记作φm（r），即

■

再对m+1，重复以上过程，得到φm+1（r）

■

样本熵的算法设计如下：

首先，将数据序列{y（i）}按顺序组成m维向量，即：

然后定义Y（i）和Y（j）之间的距离d[Y（i），Y（j）]为两个向量对应元素中差值最大的一个，即：

显然，此时的Y（i）和Y（j）中其他对应元素间差值自然都小于d，再针对每一个i值计算Y（i）与剩余向量Y（j）（j=1，2，…，N-m+1）之间的距离d[Y（i），Y（j）]。

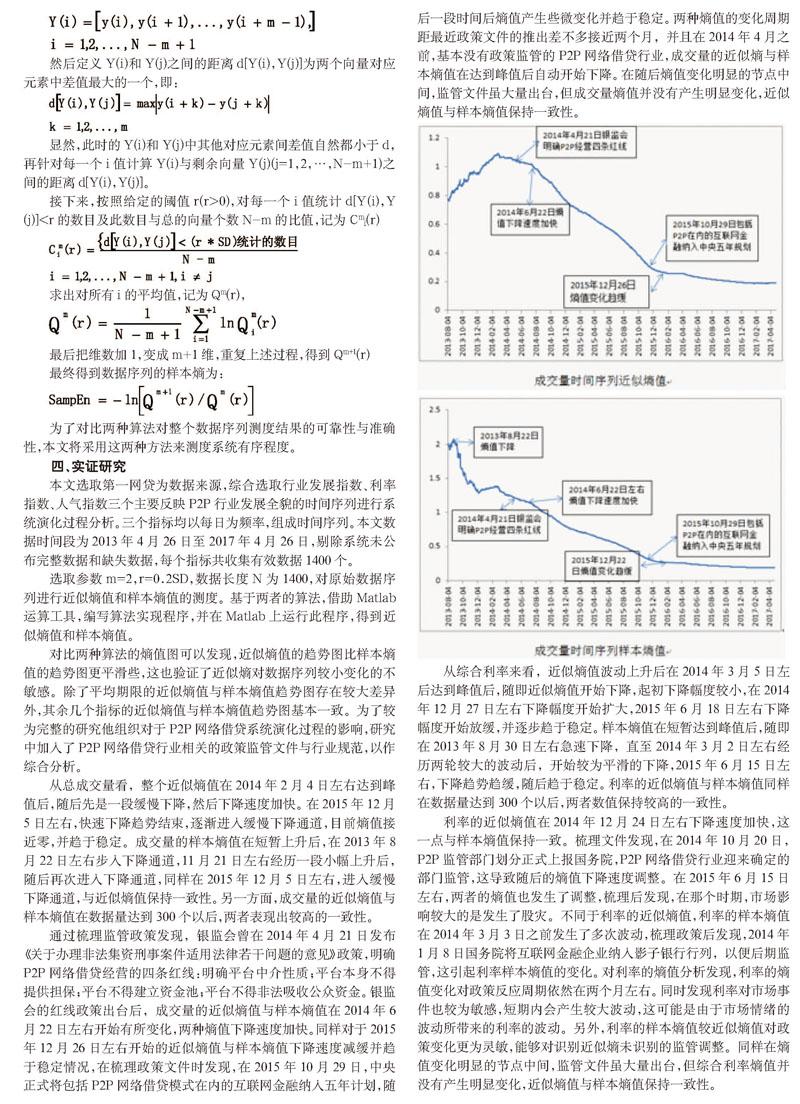
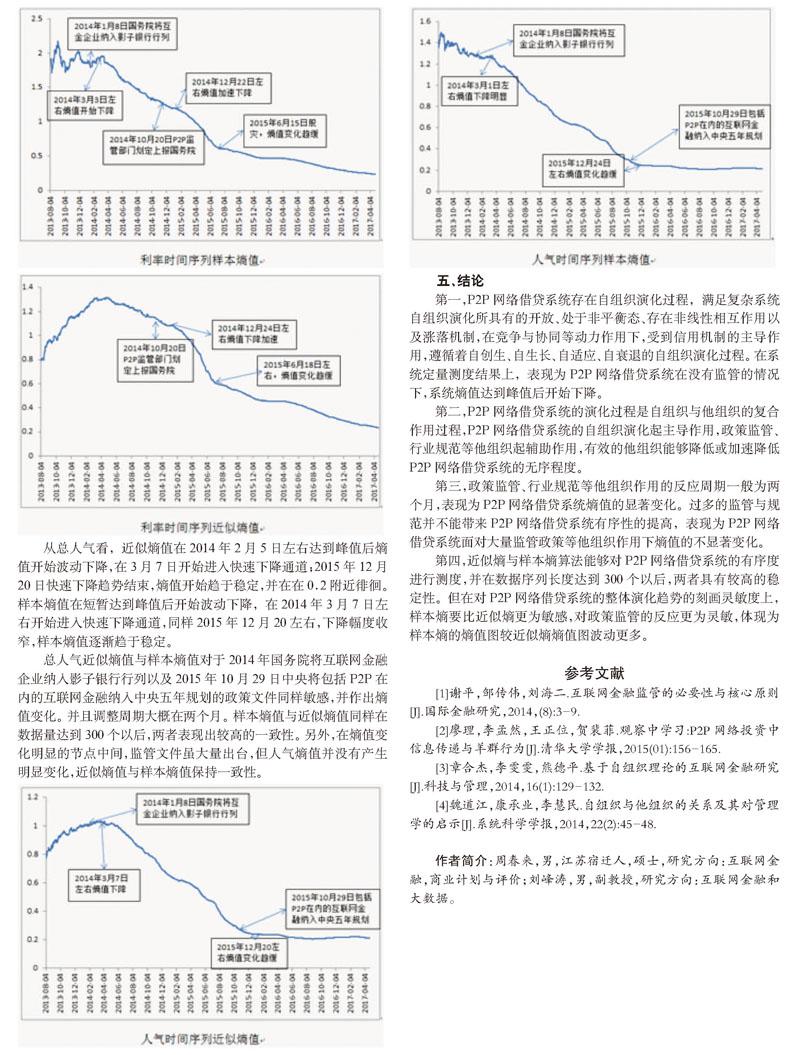
接下来，按照给定的阈值r（r>0），对每一个i值统计d[Y（i），Y（j）]

求出对所有i的平均值，记为Qm（r），

最后把维数加1，变成m+1维，重复上述过程，得到Qm+1（r）

最终得到数据序列的样本熵为：

为了对比两种算法对整个数据序列测度结果的可靠性与准确性，本文将采用这两种方法来测度系统有序程度。

四、实证研究

本文选取第一网贷为数据来源，综合选取行业发展指数、利率指数、人气指数三个主要反映P2P行业发展全貌的时间序列进行系统演化过程分析。三个指标均以每日为频率，组成时间序列。本文数据时间段为2013年4月26日至2017年4月26日，剔除系统未公布完整数据和缺失数据，每个指标共收集有效数据1400个。

选取参数m=2，r=0.2SD，数据长度N为1400，对原始数据序列进行近似熵值和样本熵值的测度。基于两者的算法，借助Matlab运算工具，编写算法实现程序，并在Matlab上运行此程序，得到近似熵值和样本熵值。

对比两种算法的熵值图可以发现，近似熵值的趋势图比样本熵值的趋势图更平滑些，这也验证了近似熵对数据序列较小变化的不敏感。除了平均期限的近似熵值与样本熵值趋势图存在较大差异外，其余几个指标的近似熵值与样本熵值趋势图基本一致。为了较为完整的研究他组织对于P2P网络借贷系统演化过程的影响，研究中加入了P2P网络借贷行业相关的政策监管文件与行业规范，以作综合分析。

从总成交量看，整个近似熵值在2014年2月4日左右达到峰值后，随后先是一段缓慢下降，然后下降速度加快。在2015年12月5日左右，快速下降趋势结束，逐渐进入缓慢下降通道，目前熵值接近零，并趋于稳定。成交量的样本熵值在短暂上升后，在2013年8月22日左右步入下降通道，11月21日左右经历一段小幅上升后，随后再次进入下降通道，同样在2015年12月5日左右，进入缓慢下降通道，与近似熵值保持一致性。另一方面，成交量的近似熵值与样本熵值在数据量达到300个以后，两者表现出较高的一致性。

通过梳理监管政策发现，银监会曾在2014年4月21日发布《关于办理非法集资刑事案件适用法律若干问题的意见》政策，明确P2P网络借贷经营的四条红线：明确平台中介性质；平台本身不得提供担保；平台不得建立资金池；平台不得非法吸收公众资金。银监会的红线政策出台后，成交量的近似熵值与样本熵值在2014年6月22日左右开始有所变化，两种熵值下降速度加快。同样对于2015年12月26日左右开始的近似熵值与样本熵值下降速度减缓并趋于稳定情况，在梳理政策文件时发现，在2015年10月29日，中央正式将包括P2P网络借贷模式在内的互联网金融纳入五年计划，随后一段时间后熵值产生些微变化并趋于稳定。两种熵值的变化周期距最近政策文件的推出差不多接近两个月，并且在2014年4月之前，基本没有政策监管的P2P网络借贷行业，成交量的近似熵与样本熵值在达到峰值后自动开始下降。在随后熵值变化明显的节点中间，监管文件虽大量出台，但成交量熵值并没有产生明显变化，近似熵值与样本熵值保持一致性。

从综合利率来看，近似熵值波动上升后在2014年3月5日左后达到峰值后，随即近似熵值开始下降，起初下降幅度较小，在2014年12月27日左右下降幅度开始扩大，2015年6月18日左右下降幅度开始放缓，并逐步趋于稳定。样本熵值在短暂达到峰值后，随即在2013年8月30日左右急速下降，直至2014年3月2日左右经历两轮较大的波动后，开始较为平滑的下降，2015年6月15日左右，下降趋势趋缓，随后趋于稳定。利率的近似熵值与样本熵值同样在数据量达到300个以后，两者数值保持较高的一致性。

利率的近似熵值在2014年12月24日左右下降速度加快，这一点与样本熵值保持一致。梳理文件发现，在2014年10月20日，P2P监管部门划分正式上报国务院，P2P网络借贷行业迎来确定的部门监管，这导致随后的熵值下降速度调整。在2015年6月15日左右，两者的熵值也发生了调整，梳理后发现，在那个时期，市场影响较大的是發生了股灾。不同于利率的近似熵值，利率的样本熵值在2014年3月3日之前发生了多次波动，梳理政策后发现，2014年1月8日国务院将互联网金融企业纳入影子银行行列，以便后期监管，这引起利率样本熵值的变化。对利率的熵值分析发现，利率的熵值变化对政策反应周期依然在两个月左右。同时发现利率对市场事件也较为敏感，短期内会产生较大波动，这可能是由于市场情绪的波动所带来的利率的波动。另外，利率的样本熵值较近似熵值对政策变化更为灵敏，能够对识别近似熵未识别的监管调整。同样在熵值变化明显的节点中间，监管文件虽大量出台，但综合利率熵值并没有产生明显变化，近似熵值与样本熵值保持一致性。

从总人气看，近似熵值在2014年2月5日左右达到峰值后熵值开始波动下降，在3月7日开始进入快速下降通道；2015年12月20日快速下降趋势结束，熵值开始趋于稳定，并在在0.2附近徘徊。样本熵值在短暂达到峰值后开始波动下降，在2014年3月7日左右开始进入快速下降通道，同样2015年12月20左右，下降幅度收窄，样本熵值逐渐趋于稳定。

总人气近似熵值与样本熵值对于2014年国务院将互联网金融企业纳入影子银行行列以及2015年10月29日中央将包括P2P在内的互联网金融纳入中央五年规划的政策文件同样敏感，并作出熵值变化。并且调整周期大概在两个月。样本熵值与近似熵值同样在数据量达到300个以后，两者表现出较高的一致性。另外，在熵值变化明显的节点中间，监管文件虽大量出台，但人气熵值并没有产生明显变化，近似熵值与样本熵值保持一致性。

五、结论

第一，P2P网络借贷系统存在自组织演化过程，满足复杂系统自组织演化所具有的开放、处于非平衡态、存在非线性相互作用以及涨落机制，在竞争与协同等动力作用下，受到信用机制的主导作用，遵循着自创生、自生长、自适应、自衰退的自组织演化过程。在系统定量测度结果上，表现为P2P网络借贷系统在没有监管的情况下，系统熵值达到峰值后开始下降。

第二，P2P网络借贷系统的演化过程是自组织与他组织的复合作用过程，P2P网络借贷系统的自组织演化起主导作用，政策监管、行业规范等他组织起辅助作用，有效的他组织能够降低或加速降低P2P网络借贷系统的无序程度。

第三，政策监管、行业规范等他组织作用的反应周期一般为两个月，表现为P2P网络借贷系统熵值的显著变化。过多的监管与规范并不能带来P2P网络借贷系统有序性的提高，表现为P2P网络借贷系统面对大量监管政策等他组织作用下熵值的不显著变化。

第四，近似熵与样本熵算法能够对P2P网络借贷系统的有序度进行测度，并在数据序列长度达到300个以后，两者具有较高的稳定性。但在对P2P网络借贷系统的整体演化趋势的刻画灵敏度上，样本熵要比近似熵更为敏感，对政策监管的反应更为灵敏，体现为样本熵的熵值图较近似熵熵值图波动更多。

参考文献

[1]谢平，邹传伟，刘海二.互联网金融监管的必要性与核心原则[J].国际金融研究，2014，（8）：3-9.

[2]廖理，李孟然，王正位，贺裴菲.观察中学习：P2P网络投资中信息传递与羊群行为[J].清华大学学报，2015（01）：156-165.

[3]章合杰，李雯雯，熊德平.基于自组织理论的互联网金融研究[J].科技与管理，2014，16（1）：129-132.

[4]魏道江，康承业，李慧民.自组织与他组织的关系及其对管理学的启示[J].系统科学学报，2014，22（2）：45-48.

作者简介：周春来，男，江苏宿迁人，硕士，研究方向：互联网金融，商业计划与评价；刘峰涛，男，副教授，研究方向：互联网金融和大数据。