矿山深部工程FLAC3D初始地应力场生成的速度-应力边界法

刘俊广 陈庆发 尹庭昌

(广西大学资源环境与材料学院，广西 南宁 530004)

随着国民经济的快速发展，诸如水利水电开发工程、固体矿床资源开发工程、国防工程等大型深地岩石工程在我国西部山区广泛建设[1]，本研究将这些布置在山区、埋藏于地下的岩石工程统称为矿山深部工程。

当前，数字模拟技术已成为岩石工程稳定性计算与分析的主要手段，其中初始地应力场生成是否准确是保障工程模拟仿真真实性的前提，很大程度上影响着计算结果的可靠性[2]；随着数值模拟技术快速发展，FLAC3D软件已成为岩土工程行业数值分析的最主要的工具之一。

有关岩石地下工程初始地应力场生成，已有部分学者利用FLAC3D软件开展了相关研究。如：Li等[3]提出了FALC3D利用偏最小二乘回归分析方法拟合地应力场，提高了局部地应力异常区域的拟合精度；罗润林等[4]在粒子群算法原理和地应力反演法的基础上，利用Fish语言建立了岩体初始地应力反演程序，提高了反演的精度和效率；张国强等[5]利用FLAC3D对初始地应力场模拟方法进行了改进，建立了三维非线性地应力反演分析数值模型，采用神经网络结构分析法，对不同深度侧向系数进行了反演，通过将计算结果与现场实测值对比，证明了其地应力反演的合理性；于崇等[6]基于现场地应力测试资料，提出了新的地应力反演方法，利用FLAC3D软件对初始地应力场进行了模拟，反演结果与实测值误差较小，精度较高；Saati和Mortazavi[7]基于实测地应力，利用FLAC3D构建了三维数值模型，对地应力进行了反演分析，模拟结果与实测地应力吻合较好；裴启涛等[8]采用遗传神经网络法和FLAC3D对研究区域建立了大尺度和小尺度模型，分别进行了初始地应力一次反演和二次反演；凌影[9]借助BP神经网络，根据测点应力数据利用FLAC3D反演了计算区域的初始地应力场，与实测地应力有较高的符合度；李仲奎等[10]基于FLAC3D数值分析软件，针对深埋工程构造应力场的模拟提出了快速应力边界法，为深部地应力场模拟提供了参考。

上述研究所采用的边界条件加载方法通常为速度边界法和快速应力边界法。利用这2种边界加载方法，在矿山深部工程初始地应力场建模分析过程中，存在“地应力与实际不符”、“边界条件施加困难和浅部区域地应力与实际不符”的问题。

针对上述问题，本研究提出矿山深部工程FLAC3D初始地应力场生成的速度-应力边界法，并通过算例分析验证了新边界加载方法的合理性。

1 速度-应力边界法的提出

1.1 初始地应力场生成的常用方法

(1)速度边界法。对于矿山浅部工程，初始地应力场主要为自重应力场。自重应力场的模拟通常采用限制边界位移，使模型在自重应力的作用下达到平衡，但在FLAC3D中边界条件的定义中无通常的位移边界条件，而是速度边界条件，即通过设置模型边界节点的速度实现对边界位移的控制。

速度边界法通过设置模型侧面及底面速度[11-12](通常设定某方向速度为0)，进而限制边界法向位移以得到模型的自重应力场，如图1所示。

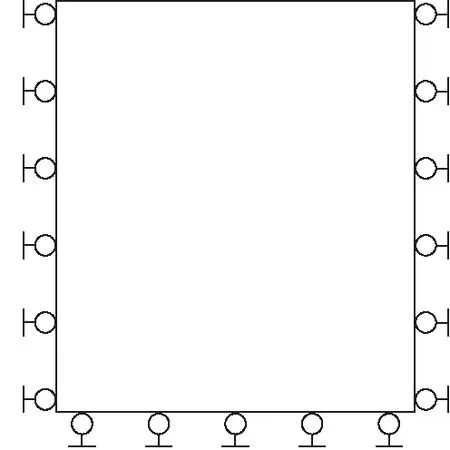
图1 速度边界约束

(2)快速应力边界法。对矿山深部工程，初始地应力场通常为自重应力场和构造应力场的叠加。FLAC3D中是模型内应力与自重应力平衡得到初始地应力场，但往往只是自重应力场，与深埋工程初始地应力场不相符。为模拟深部工程初始地应力场，文献[10]提出了快速应力边界法。该方法不设置模型速度边界条件，而根据实测地应力数据在模型表面施加应力边界条件并保持应力恒定(见图2)，使模型在给定的构造应力条件下达到平衡，进而得到深埋工程初始地应力场。

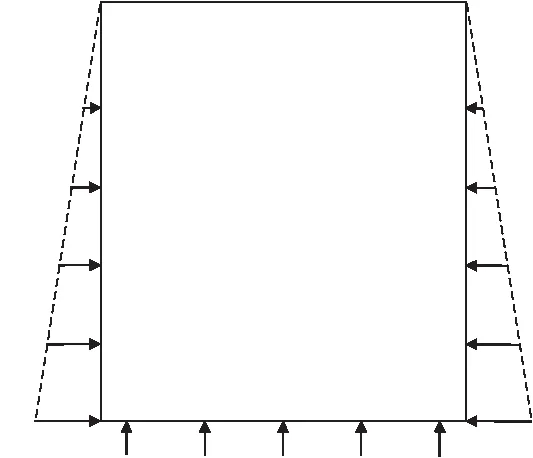
图2 应力边界约束

快速应力边界法因未设置位移边界条件，在平衡过程中模型可能产生较大位移，可通过增大岩体体积模量和剪切模量减小模型位移或平衡后将所有节点位移清零的方式控制模型的变形。

1.2 常规边界加载方法的局限性分析

1.2.1 速度边界法

速度边界法通常用于浅埋工程和地表工程的初始地应力场模拟，往往只是自重应力场，对深埋工程的初始地应力场不再适用，且对网格和节点较多的大型模型求解平衡所需时间长。

1.2.2 快速应力边界法

快速应力边界法主要用于深部工程初始地应力场的模拟，对模型地表初始地应场模拟存在不足之处，且对矿山深部工程边界条件施加困难。

在FLAC3D数值分析过程中，如以P水平面为模型上表面，采用快速应力边界法对矿山深部工程进行初始地应力场的生成，如图3所示。

图3 矿山深部工程应力边界

该方法存在以下问题：

(1)A区域无应力场存在，采用快速应力边界法造成此区域地表地应力增大，与实际不符。

(2)B区域缺少边界条件，且地应力降低，甚至可能出现反重力现象，与实际不符。

(3)模拟得到的地表初始地应力场与实际自重应力场不符，浅部初始地应力场模拟存在不足。

1.3 速度-应力边界法的提出

(1)速度-应力边界法内涵。针对速度边界法和快速应力边界法在矿山深部工程初始地应力场模拟存在不足，综合这2种边界加载方法的优点，提出了“速度-应力边界法”。

速度-应力边界法的实质是将模型划分为上、下2部分，分别采用速度边界约束条件和应力边界约束条件，使模型在给定条件下达到平衡，得到矿山深部工程初始地应力场。

如图4所示，以P0水平为分界面，P0水平以上模型边界范围采用速度边界约束条件，P0水平以下模型边界范围采用应力边界约束条件。

速度-应力边界法下部未设置位移边界条件，在平衡过程中可能产生较大位移，但上部设置位移边界约束，因此只能通过增大岩体体积模量和剪切模量控制下部位移变形，进而降低分界处边界条件对模型应力的影响。

(2)速度-应力边界法边界条件范围划分探讨。速度-应力边界法中边界条件范围的确定，受诸多因素影响，如地形地貌、地质构造、岩体性质等。因此，边界条件加载范围是随工程实际而变化的动态值，即P0水平面为范围值，无固定值。

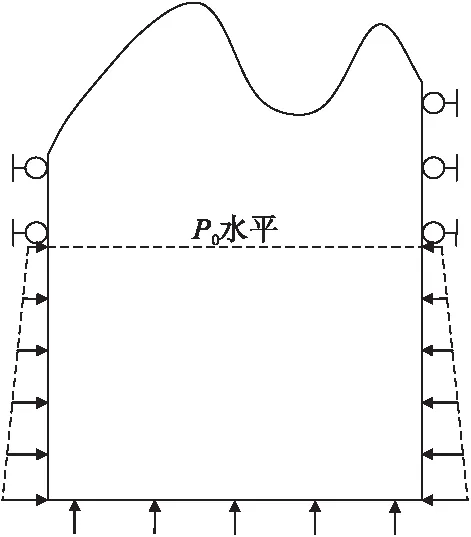
图4 速度-应力边界约束

实际应用中，应根据实测地应力值采用多次试计算方法，至地表对地应力分布影响较小，确定速度-应力边界法边界条件加载范围。

2 速度-应力边界法的算例验证

2.1 算例验证步骤

速度-应力边界法验证一般步骤如下。

(1)根据地质资料构造三维分析FLAC3D数值模型。

(2)分别采用速度边界法、快速应力边界法和速度-应力边界法，对模型初始地应力场进行模拟，并与实测地应力值进行对比分析。

(3)基于实测地应力值，通过对比不同方法初始地应力场模拟结果，分析验证速度-应力边界法的可行性和合理性。

2.2 算 例

2.2.1 FLAC3D模型构建

某锌多金属矿体为复杂多层缓倾斜薄矿体，面积大、矿层薄、品位低、矿体形态复杂。目前，该锌多金属矿体已探明主要有大矿体78号、82号、28-2号、94号、95号、96号和97号等7层矿体。

基于锌多金属矿地质资料，本研究数值模拟确定有5种模型力学介质，其岩体力学参数见表1。

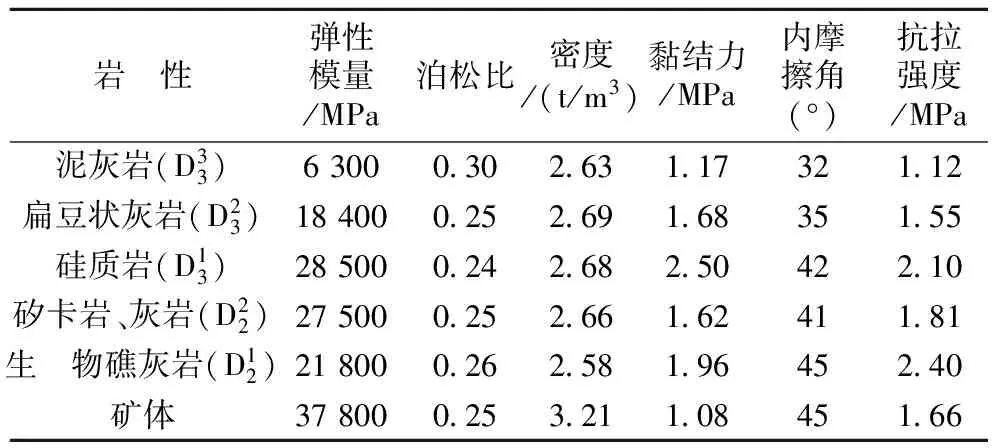
表1 锌多金属矿区岩体力学参数

根据《锌铜矿岩石物理力学性质与原岩应力场测定》和《锌多金属矿深部岩石力学与地压研究》提供的原岩应力测试结果，得到不同水平的应力值，如表2所示。

表2 锌多金属矿区地应力

三维模型构建如图5所示。

图5 三维数值分析模型

2.2.2 初始地应力场模拟结果分析

(1)采用速度边界法对锌多金属矿初始地应力场进行模拟，模型达到平衡后，生成的初始地应力场云图，如图6所示。模型底部初始地应力模拟值为：σxx=-9.183 8 MPa，σyy=-9.134 7 MPa，σzz=-25.979 MPa。发现σxx和σyy远小于地应力实测值，与实际不符，表明速度边界法在矿山深部工程模拟初始地应力场存在缺陷。

(2)采用快速应力边界法对锌多金属矿初始地应力场进行模拟，模型达到平衡后，生成的初始地应力场云图，如图7所示。在模型+305，+150，+90和 +30 m水平上各随机选取6个点，分别测得σxx、σyy和σzz值，如表3所示。

由表4和表5可知，采用快速应力边界法模拟的矿山深部工程深部初始地应力值与地应力实测值基本一致，表明快速应力边界法模拟深部初始地应力场可行。

图6 速度边界法初始地应力云图

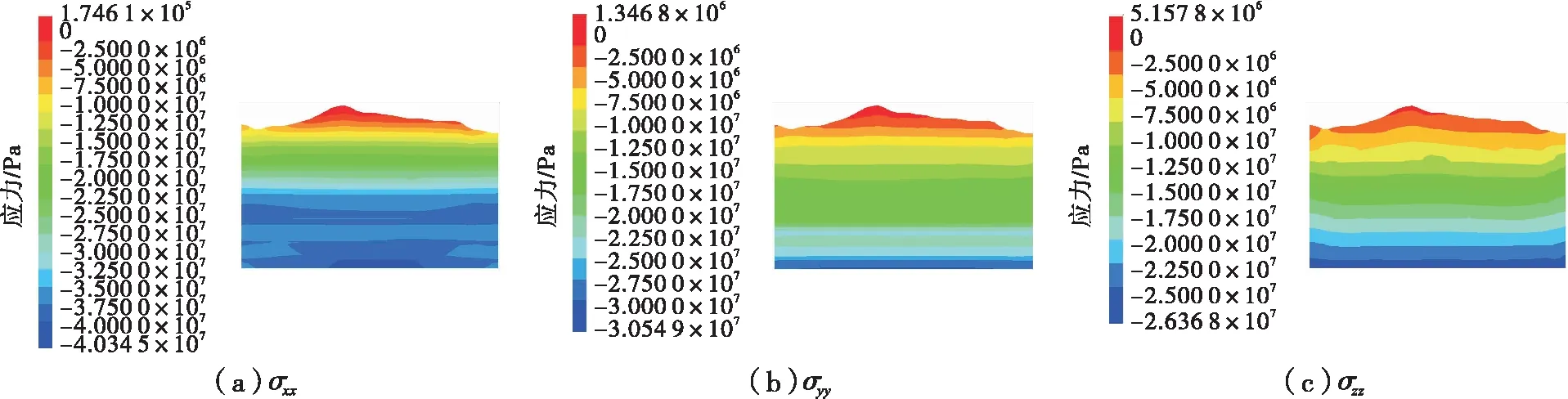
图7 快速应力边界法初始地应力云图

表3 快速应力边界法地应力模拟值

表4 快速应力边界法地表地应力

在模型地表随机选取6个点，分别测得σxx、σyy和σzz值，如表4所示。

由表4和图7可知，采用快速应力边界法生成的地表应力σxx和σyy普遍偏大，且均大于σzz，在模型顶部出现拉应力，与实际不符；表明快速应力边界法对模型地表初始地应场模拟存在缺陷。

(3)首先采用多次试计算方法，确定了速度-应力边界法速度边界条件范围约为最低标高下埋深30 m。

采用速度-应力边界法对锌多金属矿初始地应力场进行模拟，模型达到平衡后，生成的初始地应力场云图，如图8所示。在模型+305 m，+150 m，+90 m和+30m水平上各随机选取6个点，分别测得σxx、σyy和σzz值，如表5所示。

由表4和表5可知，采用速度-应力边界法模拟的矿山深部工程深部初始地应力值与地应力实测值基本一致，表明速度-应力边界法模拟深部初始地应力场可行。

在模型地表随机选取6个点，分别测得σxx、σyy和σzz值，如表6所示。

由表6和图8可知，采用速度-应力边界法生成的地表应力σxx和σyy均小于σzz，符合自重应力场应力分布规律，表明速度-应力边界法对浅部初始地应力场的模拟具有合理性。

将表4、表5和表6中σxx、σyy和σzz应力值拟合绘图，如图9所示。快速应力边界法和速度-应力边界法生成的+305 m水平、+105 m水平、+90 m水平和+30 m水平地应力与实测值基本相符，且变化规律基本一致，表明2种方法在模拟深部初始地应力场均具有可行性和合理性。

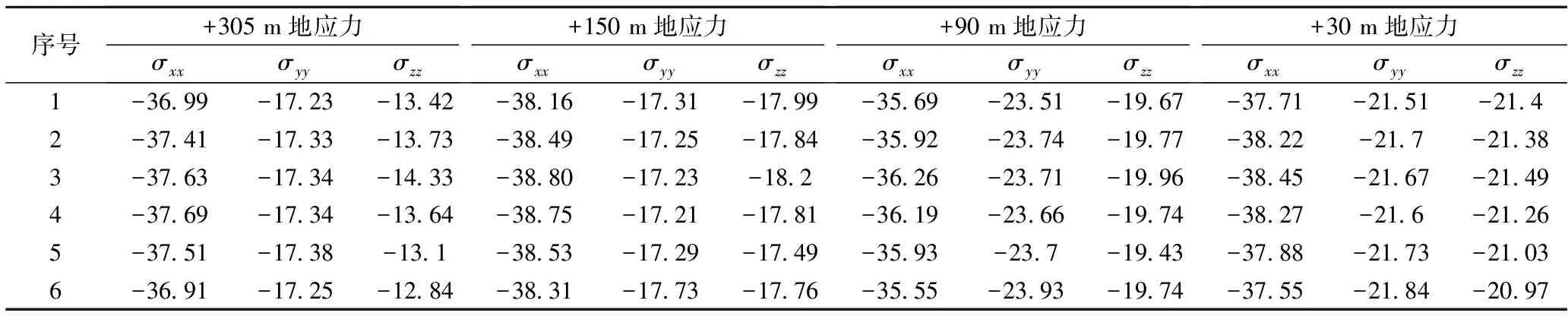
表5 速度-应力边界法地应力模拟值

图8 速度-应力边界法初始地应力云图

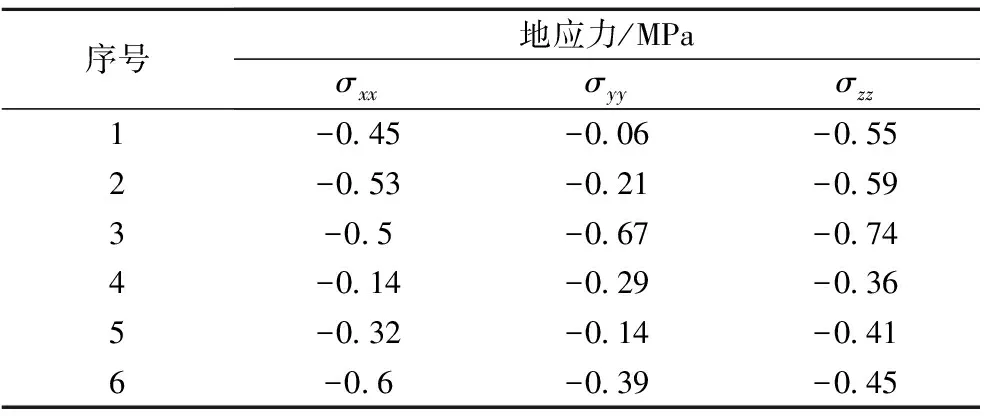
序号地应力/MPaσxxσyyσzz1-045-006-0552-053-021-0593-05-067-0744-014-029-0365-032-014-0416-06-039-045

2.2.3 综合比较分析

通过对锌多金属矿初始地应场模拟，比较分析不同方法模拟值与实测值。

(1)速度边界法仅生成自重应力场，不适用于深部初始地应力场的模拟；快速应力边界法对地表初始地应场模拟与实际不符，存在缺陷。

图9 地应力模拟值与实测值对比图

(2)速度-应力边界法生成的初始地应力场与实测值基本相符，且变化规律一致，为矿山深部工程初始地应力场模拟提供了参考。

3 结 论

(1)通过对FLAC3D初始地应力场模拟常用边界条件分析，发现速度边界法和快速应力边界法存在不足之处。针对2种方法存在的缺陷，提出了针对矿山深部工程初始地应力场模拟的速度-应力边界法。

(2)对速度-应力边界法中边界条件范围的确定进行了探讨，认为在实际应用中应采取多次试计算方法，至地表对地应力分布影响较小，进而确定速度-应力边界法边界条件加载范围。

(3)通过算例验证分析，表明速度-应力边界法模拟的初始地应力场与实际相符，且变化规律符合地应力分布规律，验证了速度-应力边界法在模拟初始地应力方面的合理性。

[1] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社,2008.

Chen Yumin,Xu Dingping.Foundation and Engineering Example of FLAC/FLAC3D[M].Beijing:China Water & Power Press,2008.

[2] 侯明勋,葛修润.岩体初始地应力场分析方法研究[J].岩土力学，2007,28(8):1626-1630.

Hou Mingxun,Ge Xiurun.Study on fitting analysis of initial stress field in rock masses[J].Rock and Soil Mechanics,2007,28(8):1626-1630.

[3] Li Yong,Guo Yunhua，Zhu Weishen,et al.A modified initial in-situ stress inversion method based on FLAC3Dwith an engineering application[J].Open Geosciences,2015,7(1):824-835.

[4] 罗润林,阮怀宁,黄亚哲,等.岩体初始地应力场的粒子群优化反演及在FLAC3D中的实现[J].长江科学院院报，2008,25(4):73-77.

Luo Runlin,Ruan Huaining,Huang Yazhe,et al.Particle swarm optimization inversion method of initial ground stress and implementation in FLAC3D[J].Journal of Yangtze River Scientific Research Institute,2008,25(4):73-77.

[5] 张国强,王桂萱.基于神经网络结构分解与FLAC3D的初始地应力场反演[J].大连大学学报,2007,28(6)：43-47.

Zhang Guoqiang,Wang Guixuan.Back-analysis of initial ground stress field based on neural network ensemble and generation of the initial ground stress field by using FLAC3D[J].Journal of Dalian University,2007,28(6):43-47.

[6] 于 崇,李海波,李国文,等.大连地下石油储备库地应力场反演分析[J].岩土力学,2010,31(12)：3984-3990.

Yu Chong，Li Haibo，Li Guowen，et al.Inversion analysis of initial stress field of Dalian underground oil storage cavern[J].Rock and Soil Mechanics,2010,31(12):3984-3990.

[7] Saati V,Mortazavi A.Numerical modelling of insitu stress calculation using borehole slotter test[J].Tunnelling and Underground Space Technology,2011,26(1):172-178.

[8] 裴启涛,李海波,刘亚群,等.复杂地质条件下坝区初始地应力场二次反演分析[J].岩石力学与工程学报，2014,33(增1):2779-2785.

Pei Qitao,Li Haibo,Liu Yaqun,et al.Two-stage back analysis of initial geostress field of dam areas under complex geological conditions[J].Chinese Journal of Geotechnical Engineering,2014,33(S1):2779-2785.

[9] 凌 影.基于FLAC3D及BP神经网络的厂区初始地应力场反演分析[J].广东水利水电，2010(11):93-95.

Ling Ying.Back analysis of initial ground stress based on FLAC3Dand BP neural network[J].Guangdong Water Resources and Hydropower，2010(11):93-95.

[10] 李仲奎，戴 荣，姜逸明.FLAC3D分析中的初始应力场生成及在大型地下洞室群计算中的应用[J].岩石力学与工程学报,2002,21(增刊2):2387-2392.

Li Zhongkui,Dai Rong，Jiang Yiming.Improvement of the generation of the initial stress field by using FLAC3Dand application in a huge underground cavern group[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(S2):2387-2392.

[11] 彭文斌.FLAC3D实用教程[M].北京:机械工业出版社，2008.

Peng Wenbin.Practical Tutorial of FLAC3D[M].Beijing:China Machine Press,2008.

[12] 李佳宇,张子新.FLAC3D快速入门及简单实例[M].北京：中国建筑工业出版社,2016.

Li Jiayu,Zhang Zixin.Quick Start and Simple Example of FLAC3D[M].Beijing:China Architecture & Building Press,2016.