自适应滤波算法在纱疵信号去噪中的应用

卢 斌，何 勇，刘传群，彭 达

（东华大学 机械工程学院，上海 201620）

自适应滤波器越来越多地被应用在工业中，与一般滤波器相比，具有能够根据系统误差来调节自身参数的特性，从而能够较好地适应环境，实现高效的自适应滤波。自适应滤波器在工业工程上应用较为广泛的是LMS自适应滤波器，LMS自适应滤波算法就是基于维纳滤波器理论的最小均方算法，具有运算量较小、程序较少、易于工程应用等优点，是实际工程中被广泛采用的自适应滤波算法。LMS算法的性能优劣主要体现在系统能否快速收敛、能否保持稳定状态以及是否具有良好的抗干扰能力，这些性能和LMS算法中的步长参数存在密切联系[6]。LMS算法中的步长参数的变化能影响算法的收敛速度、稳态误差等性能，步长值较小时算法稳态误差就会降低，但同时算法的收敛速度也会一起降低；步长值较大时算法的收敛速度就会提升，但同时算法的稳态误差也会一起增大，所以两者存在矛盾。

LMS自适应滤波算法在信号去噪、跟踪和预测等方面有诸多应用。本文首先对一些变步长LMS自适应滤波算法的原理及性能进行研究分析，再针对纱线信号数据低信噪比、变化迅速的特点，提出一种收敛速度更快同时稳态误差又较小的变步长LMS自适应滤波算法，并将其应用到纱线信号的数据滤波中，在实验中取得了良好的效果。

1 LMS自适应滤波算法原理及其性能分析

1.1 LMS自适应滤波算法

LMS自适应滤波器是自适应滤波器中的一种，其特点是应用了最小均方算法LMS的快速求值能力，算法中的误差是均方误差并且与权系数向量呈二次函数关系，从空间角度看就是一个角度向上的抛物曲面，最小均方误差就是沿着抛物曲面下降方向找到的最小值。根据梯度的概念，滤波器输出信号与期望信号之间的误差可以用梯度来表示，梯度取到最小值时就是误差最小[2]。LMS自适应滤波算法的结构框图如图1所示。

图1 自适应滤波器的基本结构Fig.1 Basic structure of adaptive filter block diagram

图1所示的 x（n）和y（n）分别表示在 n时刻系统的输入信号和系统的输出信号，系统在n时刻的期望信号在图1中由 d（n）表示，e（n）表示系统期望信号与输出信号两者的误差。根据图1，LMS自适应算法可由如下公式表示：

式中：W（n）为滤波器的权系数向量；μ为滤波器的步长因子。

算法收敛是LMS自适应滤波算法有效的首要条件，要保证算法最终能够收敛，必须满足的条件为，经过计算化简后得到步长因子满足收敛的取值范围为

式中：λ为滤波器的输入向量X（n）的相关矩阵R的特征值。

当迭代次数趋近于无穷时，滤波器的权向量W（n）就逼近维纳解 W0[3]。

1.2 变步长LMS自适应滤波算法

固定步长的LMS算法存在收敛速度和稳态误差两个性能难以同时达到最优解的缺点，所以在工程上很难直接应用。为了解决这个问题，对固定步长的LMS算法进行优化是首要方法。变步长LMS自适应滤波算法的原理是在系统刚开始收敛的时候，期望的最优权值与滤波器当前的权值存在较大误差，根据式（1）～式（3）可知在这种情况下取较大步长可以更快地接近期望权值，即算法能以更快的速度收敛；系统在接近收敛时，即系统进入稳定状态，滤波器的当前权值与最优权值相差很小，在这种情况下如果取较大步长反而会造成误差往更大的方向偏，所以应取较小的步长保证系统的稳定性[4]。定步长LMS算法中的步长μ是固定不变的，不同的是变步长LMS算法中的步长μ（n）的值是可以根据误差e（n）进行调整的。变步长LMS算法的流程如图2所示。

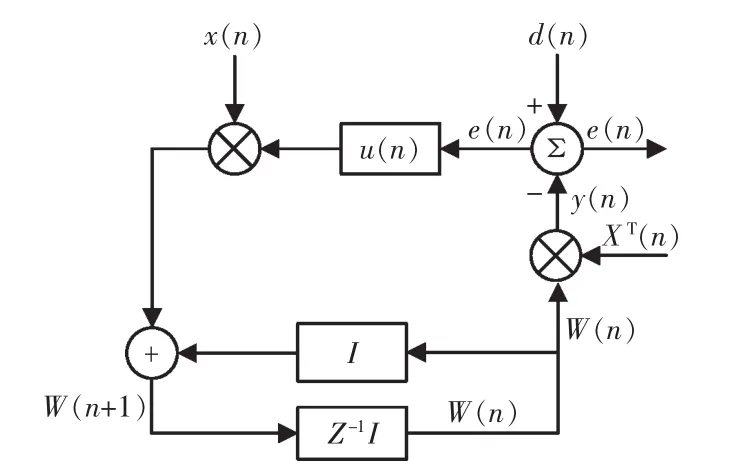
图2 变步长LMS算法框图Fig.2 Variable step LMS algorithm block diagram

为了更好地让LMS算法应用在工程上，不少改进的LMS算法被开发出来，比如归一化LMS算法、变阶数LMS算法、稀疏LMS算法等。下面对两种比较有代表性的变步长自适应滤波算法机理加以分析。

第一种是归一化LMS算法，该算法是利用输入信号X（n）的平方欧氏范数将步长“归一化”处理，该算法中步长因子表达式为

式中：μ1为初始步长，且满足：

第二种算法是一种基于Sigmoid函数变步长最小均方算法SVSLMS，该算法中步长因子的函数表达式为

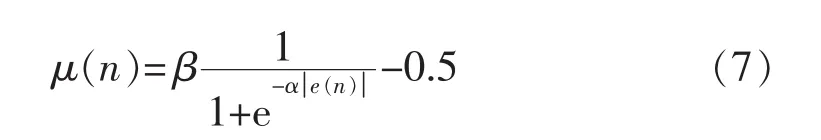
式中：α大小决定S函数曲线开口的宽窄以及上升的快慢；β大小决定S函数的高度，即S函数的最大值[5]。

由于 μ（n）随着 e（n）的减小而减小，当 e（n）为 0时，μ（n）也减小为零。但是随着算法的不断收敛，步长的改变也越来越剧烈，快速变化的步长对稳态误差会产生较大的影响，可能会引起振荡，对算法性能产生影响。

2 变步长LMS自适应滤波算法

2.1 算法改进

虽然LMS自适应滤波算法的优化原理不同，但优化的目的都是一样的，即在系统初始收敛阶段选取较大步长，以获得较快的收敛速度；而在系统处于收敛状态时，系统获得的权值和最优权值之间的误差已经较小，为了提高系统的稳定性反而需要选择较小的步长[6]。

本文根据步长调整原则，结合Sigmoid函数的一些特性，设计一种变步长LMS算法。对Sigmoid函数进行新的简单变换，即令。变换前后的函数曲线如图4所示，根据图4可以看出当自变量趋向于0时，函数值变化更慢，变化值也更小。

图3 Sigmoid函数变换前后曲线Fig.3 Transformation curve of sigmoid function

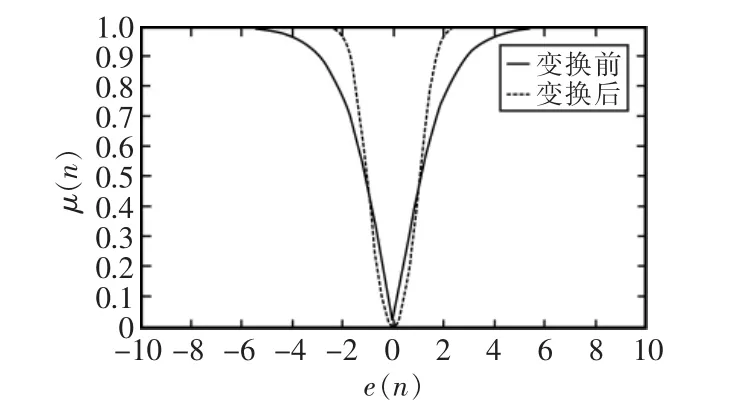
图4 Sigmoid函数新变换前后曲线Fig.4 New transformation curve of sigmoid function

由图4可以看出，两个函数曲线都遵循步长变化原则，当x接近0时，函数值变化速度减慢，函数底部趋于平滑；当x绝对值变大时，函数值随着x的变化变快。对比图中的两条曲线，可以看出本文新变换后的曲线在x绝对值较大时函数值变化速度比变换前更快，并且在x接近0时，函数值变化速度比变换前缓和，由此得出新变换后的函数更好地遵循步长原则性能。

将上述函数的x，f（x）变量换成定步长LMS算法中的 e（n），μ（n）变量，得到一个e（n）和μ（n）的新函数，即新的步长因子：

为了更好地分析步长因子与误差之间的关系，引入α、β两个参数，得到一个改进的非线性函数模型：

下面分别讨论这两个参数对函数模型性能的影响，并分析其可能的取值。

图5所示为 α 分别取 0.5、1、1.5、2，β取 1时的步长因子μ（n）与误差e（n）的函数模型曲线。

图5 参数α变动时的函数模型曲线Fig.5 Function model curve when parameter α is changed

由图5所示可知，这4条曲线均满足步长调整原则。当误差为1时（此时误差比较大），图中大多数曲线都已经达到或者接近步长因子的最大值，说明此时的收敛速度非常快，步长因子减小十分迅速；在误差逐渐较小为0的过程中，步长因子也逐渐减小为0，并且在误差值趋向0时，步长因子变化越来越缓慢，有利于减小稳态误差。

通过以上分析和图5所示可知，总体上看，α值越大，在误差比较大时步长因子减小迅速但是稳态误差也会增大，α值越小，在误差比较小时稳态误差很小但是收敛速度较慢。因此，综合以上分析，本文选择的α=0.5能保证在误差较大时步长因子曲线能更快地收敛，而且在误差趋近于0时变化逐渐缓慢，稳态误差小。

图6 参数β变动时的函数模型曲线Fig.6 Function model curve when parameter β is changed

由图6所示可知，这4条曲线均满足步长调整原则。在初始收敛阶段，步长因子随着误差变化迅速；在算法收敛后，步长因子随着误差变得比较缓慢，稳态误差较小。总体上看，β取值太大时步长因子收敛较快但是在误差较小时容易出现稳态误差，β取值太小时步长因子收敛较慢但是在误差接近0时较为稳定。因此，综合上述分析，本文选取β=0.02使系统性能达到最佳。

综上所述，本文最终设计出一个变步长因子μ（n）与e（n）的非线性函数模型：

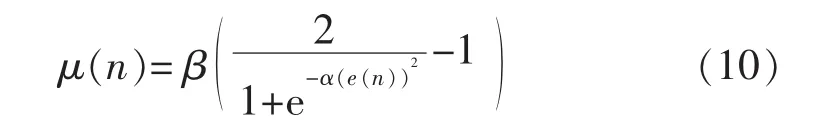
结合式（1）～式（3），本文提出的一种变步长LMS自适应滤波算法可由如下公式表示：

2.2 算法参数的仿真

在确定了算法的参数后需要对其进行仿真检验，仿真条件为输入信号sin2πt+cos2πt，叠加randn随机噪声，滤波器阶数采用2阶，采用二阶线性自适应预测来估计变步长自适应算法中的参数α、β对滤波性能的影响，采样点数为1024，为了减少误差，本文选择求出200次独立仿真的统计平均值作为结果，最后得出误差收敛图。

如图7所示，本文提出的LMS自适应滤波算法中的误差迅速减小并保持稳定，具有很好的收敛性能，可以调整参数α、β来控制函数的模型。在具体工程应用中，可以根据不同的工作环境和输入信号来调整并确定合适的参数α、β，使系统达到一个最佳状态。

图7 采用新算法的收敛曲线Fig.7 Convergence curve using the new algorithm

2.3 算法性能分析

本文中变步长LMS算法能快速收敛，比定步长LMS算法更加柔性，适应性更强，并且在初始时误差下降较快，所以系统在初始状态时能快速到达稳定。在后面区域稳定时，误差一直稳定在某个区间，基本稳定在0附近。本文使用Matlab软件对算法进行仿真测试，得到的结果如图8所示。在图8中可以看到新算法滤波性能明显优于原算法，特别是滤波速度，新算法在0.1处就基本完成滤波。

图8 算法仿真测试Fig.8 Algorithm simulation test

图9 原始纱线信号Fig.9 Original yarn signal diagram

3 算法在纱线信号滤波中的应用及分析

3.1 应用背景

纱线信号的处理是电子清纱器最重要的部分，纱线信号的去噪是其中一个关键步骤。纱线信号曲线通常表现为在一较稳定的平均值附近波动，并且在时域上信噪比较低[8]。同时，由于粗节、细节、异纤等纱疵，纱线信号中经常会出现一些异常值。由于纱线信号的特点要求采用的滤波器具有快速处理能力，以满足工程需要，这就需要采用具有学习功能的滤波器来取得满意的效果[9]。

3.2 算法应用及分析

为了能更好地对纱线信号进行处理，设计出针对纱线信号的滤波器。本文首先利用ADC转换器采集纱线信号并导入到Matlab中，这样方便观察算法的性能并调试参数[10]。本文提出的变步长LMS自适应滤波算法可以将信号中的噪声较好地去除，为下一步的模式识别做好准备。

本文将新的LMS算法应用到纱线信号的滤波中，图9中第一幅图所示为检测到的一段纱线的信号图，采样频率为20 kHz，图中纵坐标代表信号的幅值[11]。期望信号表示的是理想状况下检测到的纱线疵点信号图，图中表示纱线出现两处不同的疵点，其中图中第一处峰值代表细结，第二处峰值代表粗结。

用本文提出的变步长LMS自适应滤波算法对纱线信号进行处理后得到的信号如图9（d）所示。从图中可以看出，新算法不仅能很好地去除信号中的噪声，而且相比于原固定步长算法，纱疵信号经过新算法处理后与理想信号更接近，并且在第二次纱疵出现时能更快收敛。检测过程中纱线速度为200 m/min，两处纱疵距离为1.64 m。可见经过自适应滤波算法滤波后原信号中的大量噪声已经被很好地滤去了，并且有较好的收敛性。算法的误差收敛图如图10所示，从图中可以看出误差下降很快并且第二次误差值更接近0。

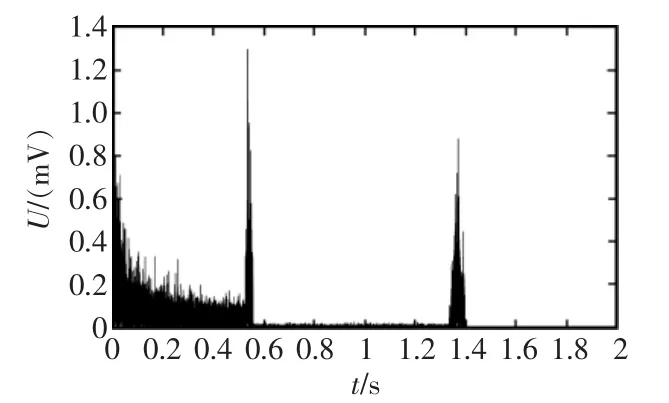
图10 误差收敛图Fig.10 Error convergence graph

4 结语

本文对一般定步长LMS算法和文中提出的变步长LMS算法进行了对比分析，步长因子的大小能够影响算法的性能，步长因子需要在系统初始阶段能够快速变化以加快收敛速度，在系统收敛后能够缓慢变化以减小稳态误差。本文在步长因子选取原则的基础上，通过仿真选取适合纱线检测的变步长自适应滤波算法，结果证明算法具有较好的收敛性和稳态性。根据纱线信号的特征，本文利用变步长自适应滤波算法对纱线信号进行滤波处理，在纱线速度为200 m/min的条件下取得了较好的效果，为进一步对纱疵的精确识别和处理打下基础。

参考文献：

[1]Turan C，Salman M S，Eleyan A.A new variable step-size block LMS algorithm for a non-stationary sparse systems[C]//Twelve International Conference on Electronics Computer and Computation.IEEE，2015：1-4.

[2]Zhu Z，Gao X，Cao L，et al.Analysis on theadaptive filter based on LMS algorithm[J].Optik-International Journal for Light and Electron Optics，2016，127（11）：4698-4704.

[3]Garg R，Kohli A K.Parameter estimation and tracking of sinusoid using variable-step-size LMS algorithms[J].Optik-International Journal for Light and Electron Optics，2016，127 （22）：10953-10960.

[4]Agarwal R K，Hussain I，Singh B.Integration of single-stage SPV generation to grid using admittance based LMS technique[C]//IEEE International Conference on Emerging Trends in Electrical，Electronics&Sustainable Energy Systems，IEEE，2016.

[5]贺远，刘刚，宁尚昆.无线数据传输系统及自适应滤波器的设计[J].自动化与仪表，2015，30（11）：26-30.

[6]周基阳，徐声伟，林楠森，等.一种提取动作电位的自适应阈值算法[J].自动化与仪表，2014，29（3）：1-5.

[7]孙勇，肖勇，方彦军.基于改进自适应阈值法的指针仪表图像预处理[J].自动化与仪表，2014，29（9）：5-9.

[8]靳翼，邵怀宗.一种新的变步长LMS自适应滤波算法及其仿真[J].信号处理，2010，26（9）：1385-1388.

[9]彭继慎，刘爽，安丽.低信噪比下基于新型变步长LMS的自适应滤波算法[J].传感技术学报，2013（8）：1116-1120.

[10]徐洋，徐松涛，马健，等.基于Sigmoid二次型隶属度函数的改进LMS 算法[J].中南大学学报：自然科学版，2014（10）：3470-3476.

[11]张中华，张端金.一种新的变步长LMS自适应滤波算法及性能分析[J].系统工程与电子技术，2009，31（9）：2238-2241.