不同信噪比下混沌系统弱信号检测性能分析∗

石 敏 陈迎春 虢应华

（1.水声对抗技术重点实验室 湛江 524022）（2.91388部队 湛江 524022）

1 引言

混沌系统具有对与之内置信号频差较小信号敏感，而对噪声及与之内置信号频差较大信号免疫的特点［1～5］，据此可以检测待测信号中是否含有与混沌系统内置信号同频的微弱信号［6～10］。

仿真中发现，混沌临界状态下输入不同信噪比的信号其检测性能是不一样的，某些信噪比的信号输入到混沌系统临界状态中可能不会引起系统状态的变化，混沌系统检测弱信号是有概率的，本文中引入检测率用于表征混沌系统检测弱信号的检测性能，仿真还发现其检测性能与选取的混沌临界阈值及噪声功率均有关。

2 混沌系统微弱信号检测的基本原理

可用于任意频率微弱信号检测的duffing混沌检测系统方程为

式中，ω和γ分别为混沌系统内置信号频率和幅度；k为阻尼系数，一般取 k=0.5，（x-x3）为非线性项，ẋ和ẍ分别为x的一阶和二阶微分。

当混沌系统处于临界状态时，将带有强噪声的外界信号作为系统内部周期驱动信号的摄动引入混沌系统。噪声虽然强烈，但只是局部地改变系统的相轨迹，很难引起系统的状态迁移。而一旦输入带有与内置信号同频率的信号成分，即使幅值很小，也会使系统的周期驱动信号的幅度增加而超过临界值，导致混沌振子向大尺度周期状态的迅速过渡，最后通过识别系统的状态迁移将深陷在噪声中的微弱周期信号检测出来。这就是混沌振子能把深埋于噪声背景中的微弱信号检测出来的基本原理。

当式（1）处于混沌临界状态，即γ=γd时，加入与系统内置信号同频率的含噪信号，得到式（2）所示的方程形式：

式中，n（t）为噪声，a为待测信号的幅度，且a<< γd。

在式（2）中，令k=0.5，ω=1，a=0.01，n（t）的功率为0.01，某次仿真中，图1（a）和（b）分别给出了在系统处于混沌临界状态时（取γd=0.8258）输入白噪声和高斯色噪声时系统对应的时域图和相轨迹图，图2（a）和（b）分别给出了在系统处于混沌临界状态时，输入混有上述白噪声的信号（信噪比为-23dB）和含有上述高斯色噪声的信号时（信噪比为-20dB）对应的系统时域图和相轨迹图。其中，高斯色噪声是由高斯白噪声通过带通滤波器后得到的。

由图1和图2可见，在上述仿真中，临界状态下输入一定信噪比的含噪信号将使系统的状态发生变化，而输入噪声则不会引起系统状态变化，从而可将与内置信号同频率的微弱信号检测出来。

3 不同信噪比下的检测性能

理论上，含噪信号输入到处于混沌临界状态的混沌系统中，系统应从混沌状态迅速转化为大尺度周期状态，即系统对应的最大Lyapunov指数变为负数［11］。但仿真实验中发现在不同精度的临界阈值下输入一定信噪比的含噪信号也可能不会引起系统的状态变化，即系统对应的最大Lyapunov指数仍保持为正数。

以输入噪声为10-6，输入信号的信噪比为-10dB 为 例 ，分 别 取 γd=0.82，0.825，0.8258，0.82582725，每个临界阈值下进行100次仿真实验，得到噪声功率为10-6，信噪比为-10dB时，各仿真中系统对应的最大Lyapunov指数如图3所示。

系统状态的判断可以利用最大Lyapunov指数的符号来判断，最大Lyapunov指数大于0说明系统处于混沌态，最大Lyapunov指数小于0说明系统处于周期态，因此可定义在混沌临界状态下，输入信号后的检测率为

由图3及式（3）可知，在噪声功率为10-6，信噪比为-10dB时，混沌临界值为0.82、0.825、0.8258、0.82582725时对应的混沌系统检测率分别为0%、0%、100%、100%。可见，在不同临界阈值下，混沌振子的检测性能是不同的。表1～表8给出了白噪声功率分别为10-1～10-8，系统处于临界状态（选取不同精度的临界值）输入不同信噪比的信号时，系统对应的检测结果。

表1 白噪声功率为10-1时，系统对应的检测率

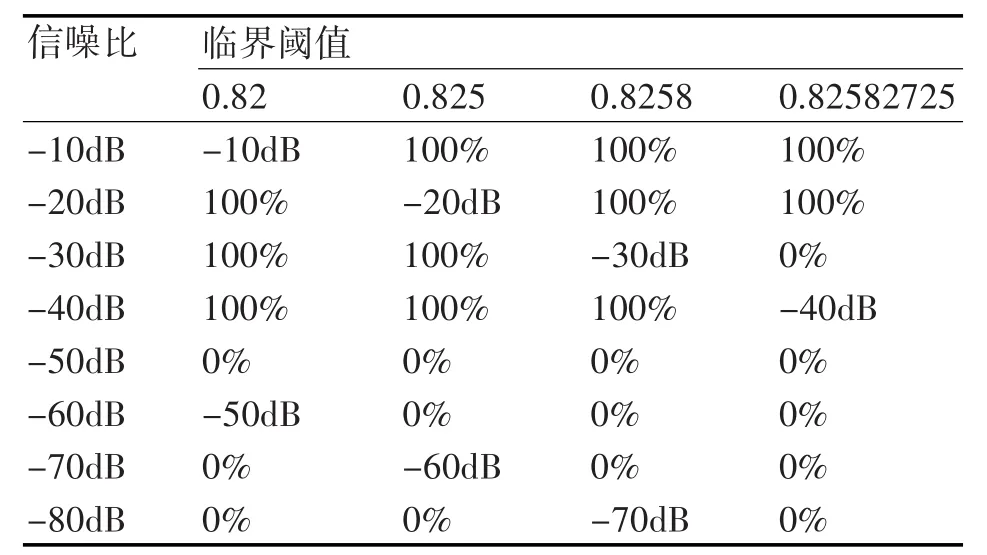
表2 白噪声功率为10-2时，系统对应的检测率

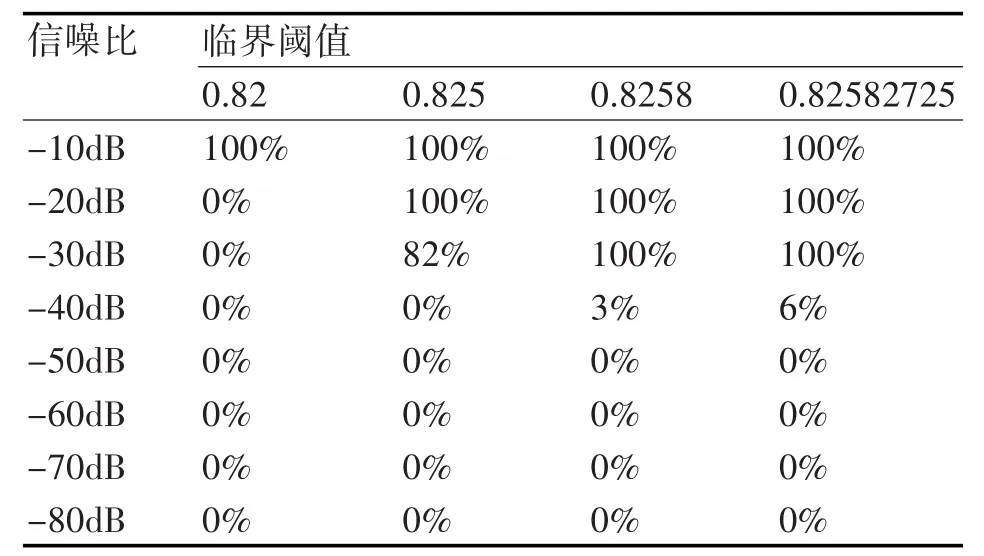
表3 白噪声功率为10-3时，系统对应的检测率

表4 白噪声功率为10-4时，系统对应的检测率

表5 白噪声功率为10-5时，系统对应的检测率

表6 白噪声功率为10-6时，系统对应的检测率

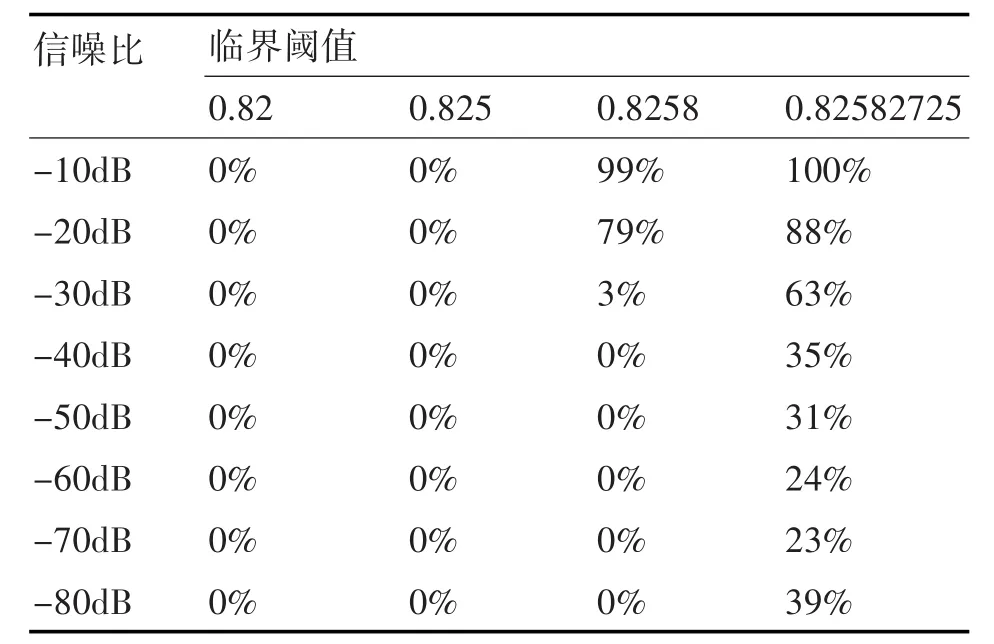
表7 白噪声功率为10-7时，系统对应的检测率

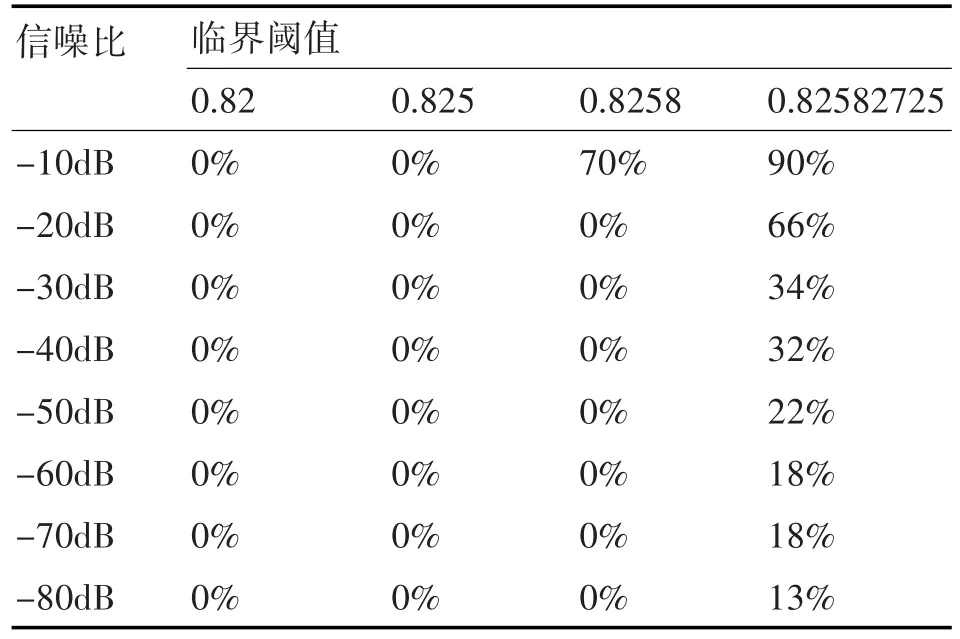
表8 白噪声功率为10-8时，系统对应的检测率

由表1～8可见，混沌系统的检测性能与输入背景噪声功率及选取的临界阈值都有关系。当背景噪声很大时，需要较大的待测信号才能使系统从混沌状态转换到大尺度周期状态。这主要是因为随着系统噪声的增大，系统的无序度将增大，系统要由无序度很高的混沌状态转变到大尺度周期状态时，就需要增加系统中的有序度来克服这种无序度的影响，而系统的有序度体现在系统外加的周期策动力上。因此，当系统的噪声较大时，系统转变到大尺度周期状态所需的周期策动力就要变大。在一定噪声功率下，临界阈值精度越高，能够检测到的信噪比越低，这主要是因为只有当选取的临界阈值与信号幅度之和大于系统真实的临界阈值时才能引起系统的相变，当选取的临界阈值精度越高时越接近于真实的临界阈值，较小的信号幅度即可引起系统的相变，因此选取较高精度的临界阈值更能检测到信噪比较低的信号，但以往的研究表明［12］，临界阈值精度越高，越有可能引起系统的虚警，误将噪声也检测为信号，因此选取合适的临界阈值是至关重要的。

4 结语

本文通过计算混沌系统在临界状态下系统的最大Lyapunov指数小于0的次数与仿真总次数的比值来定义检测率的概念，并利用检测率来表征不同噪声功率、不同精度临界阈值下，混沌系统检测不同信噪比信号的性能。检测结果表明，混沌系统检测不同信噪比信号的检测性能与噪声功率、选取的临界阈值均有关系。对于混沌系统检测而言，只有当待测信号的幅度与选取的临界阈值之和大于真实的临界阈值之后，才能引起系统的相变，从而将信号检测出来，因此对于同一噪声功率而言，临界阈值精度越高，能检测到的信噪比越低，但临界阈值精度越高也越容易引起虚警，这是一对矛盾。

［1］聂春燕.混沌系统与弱信号检测［M］.北京：清华大学出版社，2009，3：6-7，87.

［2］冀常鹏，郭伟平，姬红红.混沌振子微弱未知信号检测方法的改进［J］. 噪声与振动控制，2013，33（4）：207-211.

［3］陈军.基于混沌理论的检测系统应用研究综述［J］.甘肃高师学报，2013，18（2）：21-25.

［4］张刚，胡韬，王颖.基于Melnikov函数Duffing系统微弱信号检测［J］. 电子测量技术，2015，38（1）：109-112.

［5］Min ZHANG，Zhi-zhen LIU，Yan CAO，etal.Research and simulation on weak signal detection based on doffing oscillator and damping ratio perturbation［J］.Journal of Measurement Science and Instrumentation，2011，2（2）：161-163.

［6］朱斌.基于混沌理论的微弱信号检测［J］.电子科技，2010，23（2）：65-67.

［7］朱来普，张陆勇，谢文风等.基于Duffing混沌振子的微弱信号检测研究［J］. 无线电工程，2012，42（1）：17-20.

［8］李琳，刘春刚，石硕等.基于混沌和Lyapunov指数的微弱信号检测方法［J］.黑龙江大学自然科学学报，2012，29（4）：556-560.

［9］冉莉，王民.一种强噪声背景下微弱信号检测方法研究［J］. 信息技术，2012，2：41-45.

［10］陈新国，王洁芸.混沌振子在不同初值下检测弱信号的性能分析［J］. 仪器仪表学报，2012，33（12）：2857-2862.

［11］张宾.Lyapunov特性指数的算法研究及其在弱信号混沌检测中的应用［D］.长春：吉林大学，2004：5-6.

［12］石敏.噪声对混沌系统检测性能的影响［J］.舰船电子工程，2017，37（3）：118-121.