某水下航行体试验实施过程质量隐患源熵求解∗

余建平 刘伟才

（中国船舶重工集团公司七五〇试验场质量技术基础部 昆明 650051）

1 引言

随着科学技术及生产力水平的迅猛发展，各种电子机械产品的科技含量也越来越高，军工产品作为各类高端技术综合体的产物，其工艺复杂程度所带来的产品准备和试验过程中导致质量问题发生的因素具有更多的综合性、随机性、复杂性。为此保证过程监督到位和加强事前预防的措施，提早规避或减少质量问题的发生就变得十分重要［1］。

本文运用“产品质量熵”理论提出了“试验过程质量隐患源熵”概念，在收集了某水下航行体试验及试验准备全过程中质量问题的基础上，从产品交接及方案策划阶段、装配调试阶段、实航实施阶段、事后处理阶段分析并整理了造成质量问题的关键因素，发现产品零件质量、参试/测试设备、人为（操作）、管理是导致质量问题发生的主要因素，给出了试验过程质量隐患源熵的算法并进行了仿真求解，从而得到各隐患源的权重，并且通过仿真图形对隐患源的重要度进行排序，为后续新产品质量问题的度量和预防提供了理论借鉴［2～4］。

2 试验过程质量隐患源熵的概念

熵的概念起源于热力学，后来由Shannon引入信息领域提出信息熵理论，并开创了熵在工程技术、经济、社会应用的新纪元。熵就是描述一个系统的无序程度的变量。系统越乱，熵就越大，系统越有序，熵就越小。熵值法是突出局部差异的权重计算方法，是根据某同一指标观测值之间的差异程度来反映其重要程度的［5］。

基于产品质量与信息熵在微观概念思维方式上的相通之处，有关学者将熵引入质量管理领域来阐述产品不可控的质量损失，提出产品质量熵的概念。质量熵是质量损失的一种度量，从质量特性的角度，可用质量度对目标要求能力进行量化，即指质量完成或达到顾客满意度的状态概率［6］。从熵的角度来分析，它必然有一个与质量度相对应的质量熵来表示该质量特性的不确定度和无序度。当质量度越大时，其本身的不确定度和无序度就越小；反之，就越大。用质量度来定义其产品质量熵为：

其中，N为产品质量特性的个数、K为比例常数，同样定义为K=1/ln N、Pi为第i个的状态概率（质量度）。

基于“产品质量熵”理论，本文提出了“试验过程质量隐患源熵”概念［7］。试验过程质量隐患源熵存在于产品的各个阶段（产品交接及方案策划阶段、装配调试阶段、实航实施阶段、事后处理阶段），是对影响靶场试验过程质量潜在隐患的可能性度量。它综合反映了靶场试验全过程存在的一系列隐患问题对产品质量影响度的大小，某种试验过程质量隐患源熵越大，则试验过程质量影响度越大，从而输出的产品在试验全过程中的质量不确定性、无序度就越大，试验过程发生质量问题的可能性就越大。试验过程质量隐患源熵是试验过程质量影响度的具体表现形式，其量化结果可作为对影响试验过程权重较大的因素采取合理控制的标准［8～9］。

3 试验过程质量隐患源熵的数学模型及算法

试验过程质量隐患源熵的算法如下：1）分析产品从入场到事后处理过程导致质量问题的隐患源；2）将隐患源的原始数据进行标准化处理，得到矩阵R；3）计算各隐患源的每个指标对于影响度所有判断指标的相对比重；4）计算各隐患源值；5）计算各隐患源熵权；6）计算各试验过程质量隐患源熵综合权重。

3.1 试验过程质量隐患源熵的数学模型

试验过程质量隐患源熵的数学模型首先应分析影响试验质量的因素即试验过程质量隐患源熵，假设 X={F1，F2，…，Fn}表示有n个主要隐患源集，用 Yi={Fi1，Fi2，…，Fim}表示第i个隐患源集，yij表示第i个隐患源的第j个属性值，如果用目标函数值表示属性，则为

这样用n个隐患源的m个目标函数值表示的属性则可构成隐患源的判断矩阵为

由于不同隐患源数据具有不同的度量标准和方法，而且在数值上也可能有一定差异，因此为消除隐患源存在属性和数量级的差异，需要对原始数据采用无量纲化的方法进行标准化处理。无量纲化的方法一般有收益型、成本型、固定型、区间型，本文采用成本型无量纲化方法对隐患源集进行标准化处理，具体模型为

当影响靶场试验质量的隐患源在指标上的值完全相同时，熵值达到最大值1，熵权为0，表明该隐患源未提供任何有用信息，该隐患源可以不予考虑。当隐患源在指标上的值相差较大、熵值较小、熵权较大时，说明该隐患源是权重比较大的因素，应重点预防。各隐患源的每个指标对于该隐患源所有判断指标的相对比重为

其中：κ=1/ln m。

熵权的本质是对数据信息有用程度的度量。如果某个影响因素的熵越小，说明其值的增减程度越大，提供的有用信息量越多越有利于作出正常与异常的判断和选择，在判断该隐患源所起的作用就越大，即当该隐患源异常时，对试验过程质量的影响越大，该隐患源的熵权越大［10～12］。因此，可得第 i个影响因数的熵权为

对于靶场试验质量隐患源，使用专家法给出其主观权重为 λi（i=1，2，…，n）。主观权重是根据不同的行业、不同过程而确定的。因此，主观权重对于试验过程质量隐患源熵的确定具有实际意义。

在试验过程质量隐患源熵权与主观权重的基础上，可得第i项隐患源的综合权重为

其中：i=1，2，…n。

3.2 算法实现

利用Matlab对试验过程质量隐患源熵权重的仿真步骤如下。

1）初始化参数，分析产品从入场到事后处理过程导致试验质量问题的隐患源，将隐患源点F1，F2，…，Fn按顺序排列，将每一个隐患源点分布在m个判断指标下，获得一个判断矩阵R′。

2）根据具体情况利用成本型指标将初始判断矩阵R′进行标准化处理，得到矩阵R。

3）计算各隐患源n个指标中的每个指标j对于隐患源所有判断指标的相对比重 fij。

4）计算n类隐患源中第i个隐患源的熵值Hi，并计算第i个隐患源的熵权wi。

5）将熵权wi与专家法给出的权重 λi相结合计算第i项隐患源的综合权重wi，算法结束。

4 应用仿真

4.1 靶场试验过程质量隐患源熵组成模型

某水下航行体产品的质量控制不仅是产品研制过程的设计、材质、技术、生产等过程的质量控制，在靶场试验时，产品准备的质量控制也是决定靶场试验成败的重要因素之一。在某水下航行体湖试全过程中，应以合格零件进行装配调试为前提，即在装配调试之前需保证产品硬件质量。在产品试验实施之前，首先需要针对各分段和总体采用不同的装配调试方法和设备进行装配调试，同样在产品试验实施过程中，也要选择相应的发控、参试/测试设备。在靶场试验时，产品准备的质量控制还与组织管理和人为因素有关。根据上述分析，可建立产品靶场试验全过程质量影响因数组成模型。

4.2 靶场试验过程质量隐患源熵的仿真计算

图1为靶场试验过程质量隐患源组成模型，影响靶场试验过程质量的主要隐患源可分为四类，每一个隐患源都有不同的量化标准，隐患源的权重也不同，在计算试验过程质量隐患源熵的过程中，应具体分析，某水下航行体各类隐患源不同阶段质量问题原始数据如表1所示。

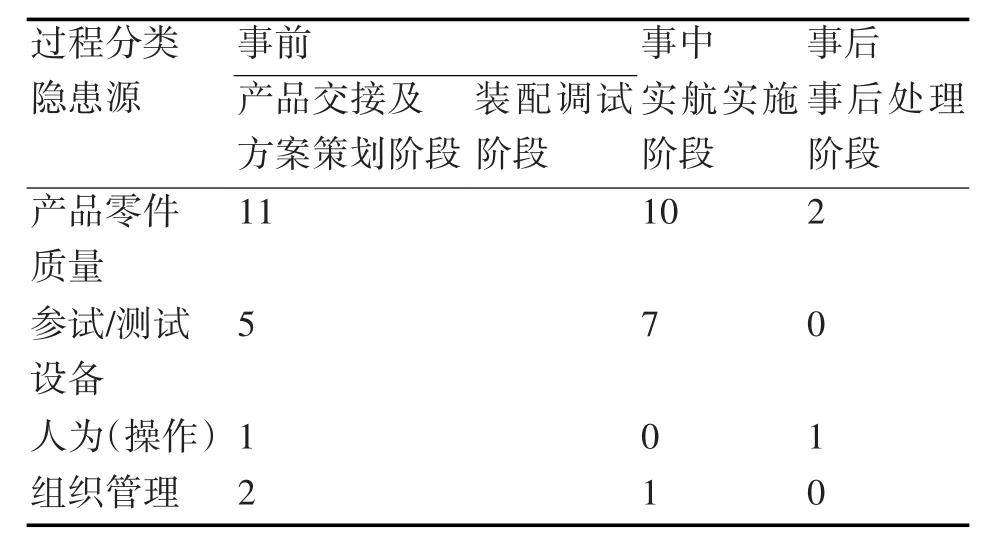
表1 某水下航行体质量问题原始数据

表2 各类隐患源不同阶段下无质量问题百分率

表2中，数据是全年该型号产品各类隐患源不同阶段质量问题统计（如表1所示），根据所得，数值越大表明该隐患源在此阶段下状态越稳定，反之则越不稳定；根据仿真算法步骤可得到如下结果：

由算法步骤1）可得模糊关联矩阵为

由步骤3）可得各隐患数据每两月与其它月份相对比重矩阵为

由步骤4）和5）可得靶场试验过程质量隐患源熵权为

由于靶场试验质量影响因数的主观权重没有通过专家判断，不能给出靶场试验质量隐患源合理的重要程度参考值，所以在此假设各质量隐患源主观权重λ均为1。

由步骤5）可得靶场试验过程质量隐患源熵的综合权重为

根据上述计算过程，可将各类隐患源的综合权重仿真如图2所示。

图2 中可以看出，通过对各类影响靶场试验质量隐患源综合权重的计算，可以很明确地得出各类靶场试验过程质量隐患源的综合权重。由仿真图可得各类隐患源隐患度的权重排序为W：｛W4＞W2＞W1＞W3｝由此得出，在靶场试验中，按2/8原则需重点控制的隐患源为W2和W4，即参试/测试设备与组织管理。由于本文质量隐患源主观权重为假设值，所以最终数据结论不反映实际情况。

本文算法不仅得出综合权重排序，并且还得出了各类隐患源隐患度的具体数值，因此可以对隐患源作针对性的控制与预防。

5 结语

本文在面向装配调试过程质量熵的基础上提出过程质量熵的概念，利用综合熵权的思想，在借鉴信息熵计算方法的基础上，将过程质量这一复杂的问题进行定量化处理，通过仿真算法来求解过程质量综合权重，从而对各类过程质量关键程度进行排序，为主动预防提供了新的思路。

［1］侯惠芳，季新生，刘光强.异构无线网络中基于标识的匿名认证协议［J］.通信学报，2011，32（5）：153-161.

［2］周彦伟，杨波，张文政.可证安全的移动互联网可信匿名漫游协议［J］.计算机学报，2015，38（4）：733-748.

［3］王波，耿如军.机械产品装配调试过程质量熵研究［J］.制造业自动化，2009，31（9）：18-23.

［4］葛红玉，张根保.机械产品装配质量缺陷源熵的算法及求解分析［J］.计算机运用与研究，2010，27（10）：3807-3809.

［5］吴红梅，金鸿章.基于熵理论复杂系统的脆性［J］.中南大学学报，2009，40（9）：347-351.

［6］丁正平，汪克夷.基于熵的直运型供应链库存协调研究［J］.计算机集成制造系统，2008，14（5）：933-936.

［7］罗良静，王静.熵权法在企业统计质量控制中的应用［J］.统计与信息论坛，2004，19（6）：5-7.

［8］刘煜，郑恒.基于熵的新产品开发决策方法［J］.科技进步与对策，2007，24（2）：155-156.

［9］王彬.基于知识的机械产品概念设计过程防错理论与方法研究［D］.北京：北京航空航天大学，2008.

［10］王旭，葛显龙，林云.供应商选择的双层规划模型及求解分析［J］.计算机工程与应用，2009，45（23）：11-14.

［11］胡俊，胡贤德，程家兴.基于Spark的大数据混合计算模型［J］.计算机系统应用，2015，24（4）：214-218.

［12］李锋刚，魏炎炎，杨龙.基于和声算法异构Hadoop集群资源分配优化［J］.计算机工程与应用，2014，50（9）：98-102.