面向数字化保护的自动文物三维重建方法研究★

吴 宁 陈佳舟 吴凯乐

(1.衢州学院，浙江 衢州 324000； 2.衢州云圈科技有限公司，浙江 衢州 324000； 3.浙江工业大学，浙江 杭州 310023)

1 概述

文物是人类在社会活动中遗留下来的具有历史、艺术、科学价值的遗物和遗迹，它是人类宝贵的历史文化遗产。对于文物的保护研究，国内外都制定了很多数字化保护方案。尽管如此，对于文物的保护仍是世界各国面临的一大挑战。对于受损文物，如何快速、有效、代价尽量小的对其进行修复；对于珍稀文物，如何在尽量少的破坏文物的情况下对其进行研究，这些仍是文物保护方面面临的难题。针对文物的数字化保护问题，本文提出利用基于图像的自动三维重建方法，构建文物的三维重建系统。通过输入一组文物图像，采用SFM+PMVS算法生成稠密点云，通过类八叉树聚类算法对稠密点云去噪，最后利用泊松曲面重建算法生成文物三维模型并进行纹理参数化。

2 相关工作

对于物体三维重建的研究很早就开始了，目前三维重建的技术趋于成熟。三维重建的方法大致分为两大类：第一类是基于光结构的三维重建方法，黄俊春[1]利用结构光技术实现了实时的物体三维重建。本文不实际基于光结构的三维重建，所以在此不再赘述。第二类是基于图像的方法，基于图像的方法也可以分为两类：一是双目立体视觉方法，T Akimoto[2]于1993年利用双目立体视觉方法用于三维重建，C L Chen[3]于2007年将双目立体视觉方法用于物体的重建，推动了双目立体视觉方法的发展。第二类是单目视觉三维重建方法，主要有基于明暗度的方法、基于光度立体视觉的方法、纹理法、轮廓法、调焦法、基于特征统计学习法和运动法。C.Harris[4]在1988年首先提出了结合角和边缘的探测方法用于物体的三维重建，迅速推动了运动法的发展。随后J.Shi[5]在1994年提出了一个更好的角度提取算法。而目前广泛使用的SIFT算法是由David Lowe[6]于1999年发表，随后更加鲁棒的SIFT算法相继被提出。在得到三维点云之后，Kazhdan[7]提出了泊松曲面重建算法，实现了三维点云到三维网格的过程。本文通过提出类八叉树聚类算法，结合SFM+PMVS和泊松算法，构建了一个三维重建系统，能够有效地用于文物的三维重建。

3 三维重建

3.1 稠密点云生成

通过相机采集待重建物体的图像数据之后，本文通过使用SFM+PMVS算法生成稠密点云。利用SIFT算法对每张图像提取特征，再对每一对图像做鲁棒的特征匹配；将所有二图匹配合并，找出相机的轨迹；通过轨迹估算相机参数场景的稀疏结构，这样可以得到物体的稀疏三维点云，然后根据PMVS算法构建出稠密的点云。由于在拍摄照片时，难免会受到物体周围的物体及光线变化的影响，因此得到的稠密点云会存在很多杂点，我们称之为噪点，如图1所示(线框外的即为噪点)。而这些噪点对于构建可编辑网格来说完全是多余的，所以在此之前有必要去除这些噪点。

3.2 类八叉树聚类算法去噪

去除稠密点云中的噪点，可以理解为将点云聚类，所有噪点归为一类，其他的归为另一类。在三维空间中，用于游戏碰撞检测的八叉树算法可以用于点云聚类，八叉树的主要思想是将整个空间分为大小一样的八个子空间，如果子空间需要继续划分，则将子空间划分为八个更小的子空间，直到达到划分边界为止。由于八叉树是划分整个空间，其实很多地方是并不需要进行空间划分的，这样会极大浪费时间。受八叉树算法的启发，本文提出了类八叉树聚类算法，能够很好的去除噪点。

算法的主要思想如下：1)预先定义子空间大小(定义正方体边长d，本文取0.2)。2)对于点云中的每个点进行遍历，根据点P的坐标信息将坐标点划归到一个子空间，后续的任何点在此子空间范围内则划分到此子空间。3)遍历所有子空间，将相邻的子空间合并。遍历完所有子空间后，也就是进一步将点进行了聚类，此时，点数量最多的子空间就是待重建物体的稠密点云。为加快速度，对所有点数目小于给定阙值(本文取10)的子空间不予以考虑。对于复杂情况，例如背景复杂，采样图像不足等，得到的噪点可能跟待重建点云连成一片。在此情况下，想自动去除这些噪点，需要通过手动交互操作。本文提出的算法不需要直接划分子空间，建立复杂的八叉树，只有当某一子空间存在点的时候才会定义一个子空间。相比于八叉树算法，运算效率有很大提高。

3.3 泊松曲面重建

泊松曲面重建基于泊松方程。泊松方程是一个比较常见的偏微分方程，在很多领域被应用，如高动态范围图像的调和映射、图像区域的无缝编辑、流体力学、网格编辑等,多重网格泊松方法已应用于高效GPU计算。表面重建过程如下：1)定义八叉树。使用八叉树结构存储点集，根据采样点集的位置定义八叉树，然后细分八叉树使每个采样点都落在深度为D的叶节点；2)设置函数空间：对八叉树的每个节点设置空间函数F，所有节点函数F的线性和可以表示向量场V，基函数F采用了盒滤波的n维卷积；3)创建向量场：均匀采样的情况下，假设划分的块是常量，通过向量场V逼近指示函数的梯度。采用三次条样插值(三线插值)；4)求解泊松方程：方程的解采用拉普拉斯矩阵迭代求出；5)提取等值面：为得到重构表面，需要选择阈值获得等值面；先估计采样点的位置，然后用其平均值进行等值面提取，然后用移动立方体算法得到等值面。对于泊松曲面重建的结果将在下一节详细讨论。

4 结果与讨论

通过本文算法，可以有效地对文物进行三维重建。接下来本文将详细介绍实验结果，并指出其中的突出点和不足之处。在有些情况下，由于条件的限制可能只能对文物进行单面图像采集工作，这样对于文物的重建就必须加入人工交互，希望得到更加逼真的效果，如图2a)所示，重建出的物体虽然有正反两面，但是物体两面成镜像对称，这其实不符合逻辑。但是本文算法也能很好地保留文物的细节信息，如图2b)所示。区别对物体单面进行采集图像并进行三维重建，对物体全方面进行采集图像，这样得到的重建效果会更加真实，能够保存文物的更多细节信息。如图3所示，由于对文物进行了足够的图像采集，文物的正反两面细节都得到了很好的

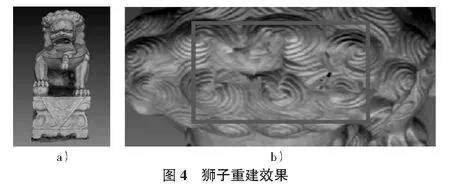
保留。在数据采集充足的情况下，数据越充足，文物重建得到的效果将更接近于实物。同样的，如果数据采集不充足，文物重建得到的效果肯定丢失细节信息。如图4a)所示，在整体看来，狮子重建的效果很好，但是由于数据采集不充足，没有提供足够的图像信息，重建出来的文物丢失了部分细节。如图4b)所示，在狮子的头部，线框标注部分的细节与其他地方相比存在明显错误。通过对不同类型的文物进行重建，对重建结果进行分析，可以得出：在数据采集充分的情况下，通过本文的算法，可以有效的重建出逼真的，能够很好地保留细节信息的文物模型。通过对文物进行三维重建，可以构建逼真的文物模型，对于文物的研究可以建立在重建的可编辑网格或者结合3D打印出的实物之上，这对于文物的研究提供了便利，同样在一定程度上起到了保护文物的作用。

5 结论与展望

通过本文的方法，可以有效的对文物进行三维重建。但是由于采集照片时的局限性，例如图像采样不充足、背景复杂、物体复杂等情况下，全自动的三维重建效果不够理想，这时候就需要进行人工交互操作。不过相比于纯手工操作来说，通过本文方法的简化之后，可以有效降低手工操作的时间，节省人力成本。理想情况下，对背景不复杂的单个文物采集充足照片，可以得出很好的效果，能够很好的保存文物的细节信息，这对于文物的保护和研究具有重要意义。在采集图像时，很难捕捉所有细节。所以针对重建结果细节丢失问题，未来可以根据研究丢失细节周围的信息来推断丢失的细节，从而补全丢失的细节信息。

[1] 黄俊春.基于结构光的实时三维重建[D].上海：华东师范大学,2009.

[2] Akimoto T,Suenaga Y,Wallace R S.Automatic creation of 3D facial models[J].IEEE Computer Graphics and Applications,1993,13(5):16-22.

[3] Chen C L,Tai C L,Lio Y F.Virtual binocular vision systems to solid model reconstruction[J].The International Journal of Advanced Manufacturing Technology,2007,35(3):379-384.

[4] Harris C,Stephens M.A combined corner and edge detector[A].Alvey vision conference[C].1988.

[5] Shi J.Good features to track[A].Computer Vision and Pattern Recognition,1994.Proceedings CVPR'94.,1994IEEE Computer Society Conference on[C].IEEE,1994:593-600.

[6] Lowe D G.Object recognition from local scale-invariant features[A].Computer vision,1999.The proceedings of the seventh IEEE international conference on.Ieee[C].1999:1150-1157.

[7] Kazhdan,Michael,Matthew Bolitho,et al.Poisson surface reconstruction[A].Proceedings of the fourth Eurographics symposium on Geometry processing[C].2006.