某轿车白车身模态试验方法分析研究
汪 坤 潘绍飞
成都理工大学工程技术学院,四川乐山 614000
目前,世界各国汽车公司竞争日趋激烈,人们对汽车品质要求也越来越高。因此,提高汽车性能,对汽车研发周期的缩短也显得更为重要。通过经验和实践的指导,我们知道,对于标杆车型可以选择市面上已有的相似车型作为参考车型,利用有限元分析法和试验分析法对其进行静态性能分析和动态性能分析,将会对所研发的新车型起到一定的参考作用。新车型的研发很大程度上取决于白车身的设计,而白车身的特性对汽车的性能有直接的影响。白车身的动态特性可以利用模态试验进行分析,它对车辆的舒适性和结构可靠性方面起着重要的作用[1]。本文以市面上某款轿车的白车身作为模态试验与分析对象,确定了白车身低阶固有频率、阻尼比和模态矩阵的模态参数,并分析了前后有无挡风玻璃对白车身动态性能的影响。
1 白车身模态试验系统
模态试验系统的组成分为四部分,其分别为激励系统、响应系统、数据采集系统和模态分析处理系统[2][4]。本试验的激励系统主要包括:信号源、功率放大器和激振器;响应系统包括:标智3向加速度传感器、信号放大器;数据采集系统:LMS SC316多通道数据采集器;模态分析处理系统包括:LMS Test.Lab 11B和计算机。对激振和响应信号的实时采集可以通过LMS数据采集器和LMS Test.Lab 11B软件实现,然后把采集到的时域信号经过模数转换盒和离散傅氏变换的快速算法变换后变成频域信号,并经过运算后可以得到频率响应函数FRF[2]。模态试验方案原理如图1所示。其中,加速度传感器的技术参数见表 1。
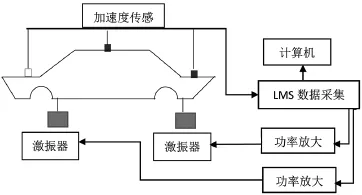
图1 模态实验方案原理
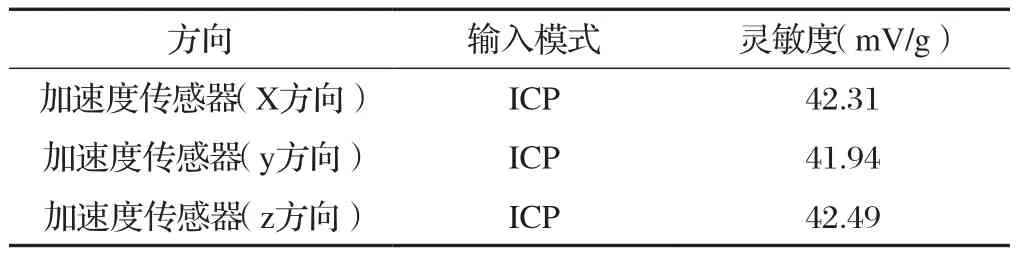
表1 传感器的主要技术参数
2 白车身模态试验方法及试验步骤
2.1 白车身几何模型的建立
在模态试验开始之前,首先需要建立白车身的几何模型,其目的是确定测试点位置以便于模态试验及模态参数的建立。白车身几何模形的建立方法分为两步:(1)选择测试的点,点的选择需要遵循:①测试点应该能够完全描绘整个白车身的形状,反映出振动模式。在一般情况下,可以选择刚度好和结构清晰的位置来保证测试点的响应信号质量。②测点应均匀对称分布在白车身上,且测点数目不宜过少,否则很难反映测试白车身的形状和振动特性;也不易过多,否则会增大试验的工作量和处理数据的繁杂;③测点不应在各阶振型的振动节点上,否则会导致无法识别模态阵型;④如果白车身某一部位有角度,在其上布置测点时,需要利用欧拉角对其进行坐标变换,否则白车身的形状无法真实的被反映出来,这样会对模态振型和识别结果造成影响。(2)根据白车身不同部位与共线或不同测量点几何特征之间的界面关系,将点与线或面连接,建立整个白车身的几何模型。本试验根据该款白车身的结构布置了169个测点并建立了几何模型,如图2所示。
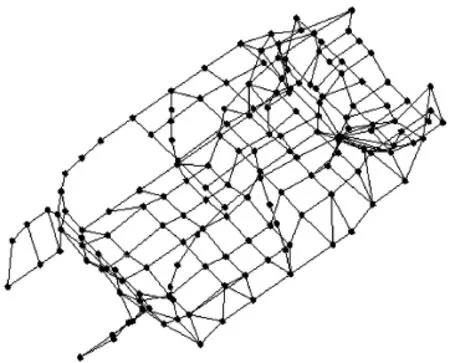
图2 白车身测点及几何模型

表2 传感器布置位置及测试点数
2.2 白车身固定方式和激振点的布置
2.2.1 固定方式的确定
模态试验一般有两种固定方式,分别为:固定支撑和自由—自由支撑;其中自由—自由支撑也分为两种:(1)空气弹簧支撑;(2)弹性绳悬挂白车身。本实验采用空气弹簧支撑,刚体模态频率为3.97Hz远小于一阶弹性模态频率 38.1Hz 的15%,满足白车身自由—自由支撑的试验要求。
2.2.2 激振点的布置
本文结合大量的试验表明,白车身模态试验的激振点的选取需要遵循:(1)选在刚度较大且有利于安放激振器的位置;(2)应避开某阶模态的节点和支撑点附近的位置,否则无法识别模态参数,影响模态阵型;(3)激振点应布置在对角线上,这样有利于结构上的激励能量更充分,获取的响应信号有较好的质量。
由试验经验可知:白车身模态试验的激振点一般最多布置两到三个,如果激振点选择过多,那样会导致频率响应函数曲线的质量变差。本次试验布置两个激振器,激振点的位置分别位于车身左后纵梁图3(a)和右前纵梁图3(b)。

图3 激振器布置位置
2.3 试验内容
对于试验中使用白车身,它的两种状态分别是:
(1)第一种状态:副车架和前后挡风玻璃都保留以及地板有阻尼;
(2)第二种状态:有副车架和没有前后挡风玻璃以及地板有阻尼。
根据试验经验我们可得知:对白车身模态试验频率的要求为:0~100Hz;因此,考虑到汽车实际行驶工况和道路激励等的因素,本次试验的白车身模态试验的试验频段取为 0~100Hz。测试时分析频率为256Hz;Spectral lines为256;频率分辨率为1.0Hz;采集时间为1.0s。
为了降低测试中噪声的影响和随机误差的影响,试验应该进行多次平均,因此本次试验采用平均技术来降低随机误差,试验平均次数为30次。由于加速度传感器数量不足,不能一次布置所有测点,需要移动传感器对白车身进行测量;为保证测量的频响函数质量可靠,应实时检测响应信号和激励信号之间的相干函数,只有相干函数在0.8以上的信号才认为有效[4]。最后,综合分析了各测试点加速度响应的频率响应函数,得到模态频率和相应的模态振型。
3 模态试验的结果与分析
对于白车身的第一种状态(有副车架、有安装玻璃、地板有阻尼),通过测试可得各响应点的频响函数,基于响应点频响函数进行模态识别,可得稳态图,如图4所示。

图4 白车身第一种状态稳态图
根据上述稳态图,可得到白车身各阶固有频率和振型。表3为白车身第一种状态的前6阶模态结果,第一种状态各阶模态振型见图5。
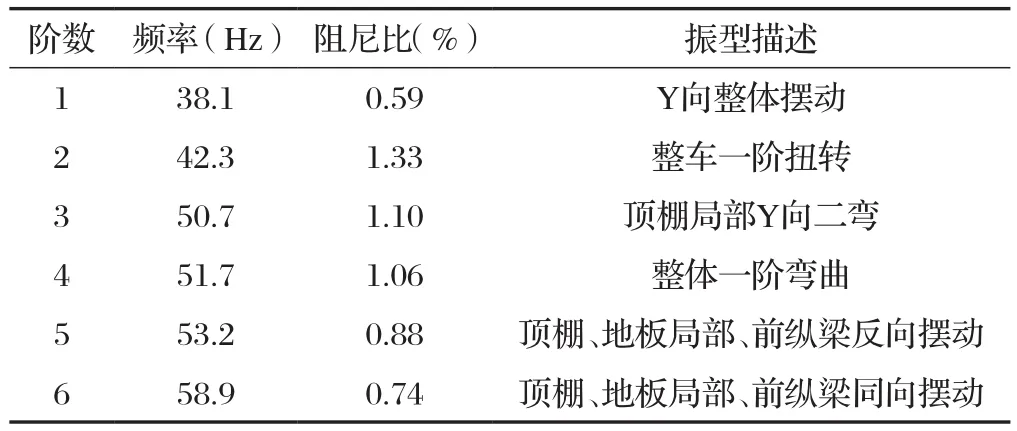
表3 白车身前 6 阶模态分析结果

图5 白车身第一种状态各阶模态振型
在白车身上拆除前后风挡玻璃,对白车身进行第二种状态的模态试验(有副车架、无安装玻璃、地板有阻尼),通过测试可得各响应点的频响函数,基于响应点频响函数进行模态识别,可得稳态图,如图6所示。
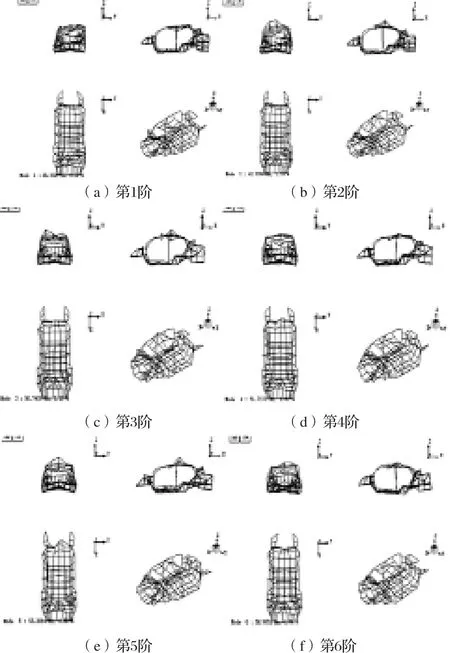
图6 白车身第二种状态稳态图
根据上述稳态图,可得到白车身各阶固有频率和振型。表4为白车身第二种状态的前5阶模态结果,第二种状态各阶模态振型见图7。
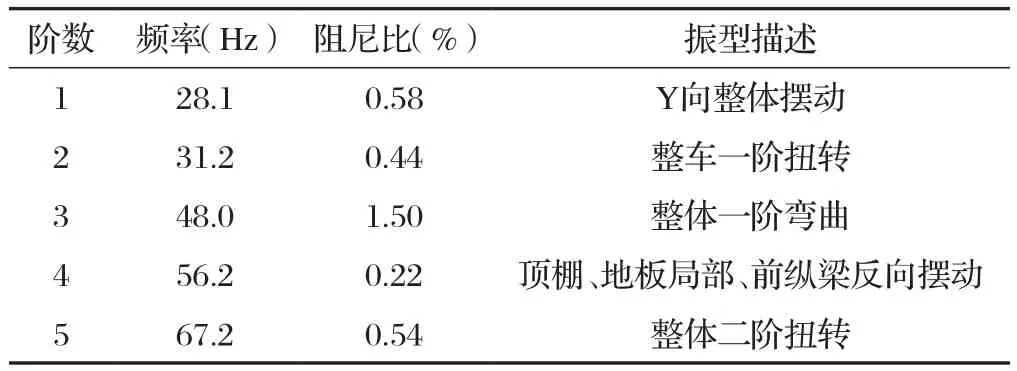
表4 白车身前5阶模态分析结果

图7 白车身第二种状态各阶模态振型
根据上述白车身两种模态分析结果可知:由于前后风挡玻璃的影响,在拆下风挡玻璃的白车身模态试验的固有频率、阻尼和振型都有一定的影响:(1)在固有频率上,前三阶都下降,后两阶都增大,其中第5阶固有频率增幅最大为26.32%;(2)对于系统的阻尼比,除了第3阶提高36.37%外,其于阶数阻尼比均减小,且第2阶减小幅度最大的为66.92%;(3)在振型方面,带玻璃的第3阶为顶棚局部Y向二弯,不带玻璃的为整体一阶弯曲;带玻璃的第4阶为整体一阶弯曲,不带玻璃的为顶棚、地板局部、前纵梁反向摆动;带玻璃的第5阶为顶棚、地板局部、前纵梁反向摆动,不带玻璃的为整体二阶扭转,表明玻璃对白车身的振动特征影响比较大。
4 结论
本文结合大量的白车身模态分析经验,对市场上某款车型的白车身进行了两种状态的分析,得到了白车身的固有频率、阻尼比和振型。通过实验结果的分析对比得知,风挡玻璃对固有频率、阻尼比和振型都有较大的影响,对于该款白车身的模态参数等的识别和结果分析,为今后的汽车研发和车身设计及优化都提供了试验依据。
[1] 李英平.汽车车身模态分析实例研究[J].汽车技术,2007(11).
[2] 戴云,邬耀明,熊毅. 某汽车白车身模态试验研究[J].轻型汽车技术,2009,10: 4-7.
[3] 张建,唐文献,马宝,等. 某轿车白车身试验模态分析[J].江苏科技大学学报(自然科学版) ,2012,2:146-149.
[4] 杨英,赵广耀,孟凡亮.某轿车白车身模态分析与试验研究[J].东北大学学报(自然科学版) ,2008,7: 1045-1048.
[5] Lan F,Chen J,Lin J. Comparative analysis for bus structures and lightweight optimization [J].Proceedings of the Institution of Mechanical Engineers. Part D,Journal of Automobile Engineering,2004,218(10):1067-1075.
[6] Kim K C,Kim C M. Astudy on the body attachment stiffness for the road noise[J].Journal of Mechanical Science and Technology,2005,19(6):1304-1312.
[7] LEE D C,WOO Y H,SANGHO LEE S H,et al.Design Consideration of the Nonlinear Specifications in the Automotive Body [J].Finite Elements in Analysis and Design,2008,44 (14):851-8611.
[8] 夏兆义,冯兰芳,王宏晓,等.某轿车白车身模态分析与优化[J],机械研究与应用,2011,3.
[9] 胡小舟,林建平,陈羹,等. 基于模态应变能及灵敏度分析白车身模态优化[J],机械科学与技术,2015,9.
[10] 张国胜,周 炜,孟凡亮,等.轿车白车身模态分析和局部刚度优化方法研究[J].公路交通科技,2010,4.
[11] 李文,李猛,金永磊,等.轿车白车身试验模态与计算模态相关性分析[J].汽车技术,2011,6.
[12] 杨年炯,钱立军,关长明.某轿车白车身模态分析[J].机械设计与制造,2012,2.

