基于GUI的周期信号频谱分析演示系统设计

孙 明

(佛山科学技术学院 电子信息工程系，广东 佛山 528000)

信号与系统课程知识体系完整，理论严谨，逻辑性强，以高等数学、工程数学及电路分析基础等课程为先导，涉及了大量的数学知识；其理论结果往往来源于复杂的数学运算及推导，不仅要求学生理解数学概念，还要求对物理概念及工程概念有较为深刻的理解。如果在学习时仅仅只记忆数学公式，不清楚其中的物理含义及工程概念，很难将信号与系统理论应用于系统设计中，从而在一定程度上会制约学生学习的主动性和创造性，难以达到培养综合能力的目的[1]。

将MATLAB的GUI编程技术引入到信号与系统课程中，可以使抽象的信号变得更加直观，易于理解[2-5]。

周期信号的傅里叶级数展开是信号与系统课程中最基本的理论知识，如果不能很好地理解这一重要概念，不仅影响本课程的学习，还会影响到后续相关课程的学习。本文设计开发了基于图形用户界面(graphical user interfaces，GUI)的周期信号傅里叶级数展开演示系统，将抽象的概念形象化，将枯燥的理论可视化，将课程中较难掌握的重要知识点以动态演示的方式展现出来，直观易懂，便于分析，使学生加深了对物理意义和工程概念的理解，在教学中取得了较好的效果[6-7]。

1 演示系统知识点

经典的傅里叶级数是当满足狄里赫利(Dirichlet)条件时，可将任一周期时间信号分解成许多不同振幅、不同频率谐波的线性组合，如式(1)所示，傅里叶级数展开形式为：

(1)

式(1)中，a0,ak,bk分别为傅里叶级数的系数，决定了不同分量的幅度。其中：

当用有限项傅里叶级数表示具有不连续点的周期信号f(t)时，若满足Dirichlet条件，所取项数N越大，越接近该信号，其傅里叶级数一致收敛[8]。当项数N→∞，即完全逼近，于是有：

(2)

用有限项傅里叶级数表示有间断点的信号时，在间断点处不可避免地会出现振荡和超量，不仅存在误差且在不连续点的两侧还会出现振荡现象，其高频起伏的最大值将趋近于一个常数，且无论N

的取值如何，约等于不连续点跳变值的8.95%，这种现象即所谓的吉伯斯现象(Gibbsphenomenon)[9-10]。

演示系统选取傅里叶级数展开、频谱分析和吉伯斯现象演示这三个重要的知识点进行分析设计，如图1所示。

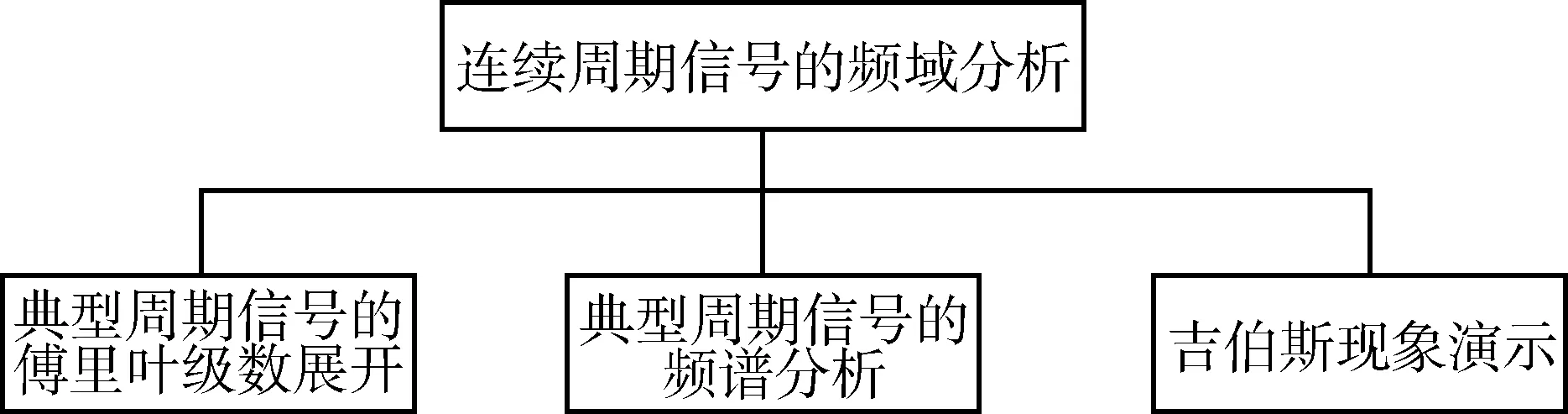
图1 知识点组成

2 演示系统设计

2.1 演示系统模块组成

界面模块包括输入、分析和图形显示三个模块，如图2所示。

输入模块包括方波、三角波、锯齿波、全波整流正弦波、全波整流余弦波、半波整流正弦波和半波整流余弦波七个典型信号；分析模块是对这些典型周期信号进行时域分析和频域分析，即分解与合成，同时在这个模块中进行吉伯斯现象的演示；图形显示模块主要是对时域分解合成波形和频谱图(幅度谱和相位谱)的显示。

图2 模块组成

2.2 GUI系统的设计

在MATLAB中创建图形用户界面的方法有图形句柄和GUIDE(graphicuserinterfacedevelopmentenvironment)两种，都需要使用M语言编程。利用图形句柄创建的GUI只有一个M文件，而利用GUIDE创建的GUI包括M文件和保存外观设计信息的fig文件两个[11-12]。

本系统无须实现复杂的功能，显然采用操作简单方便的GUIDE开发环境更适合。

基本图形对象分为控件对象和用户界面菜单对象，简称控件和菜单。GUI创建包括界面设计和控件编程两部分，主要步骤如下。

第一步，通过设置GUIDE应用程序的选项来运行GUIDE。通过命令File/New/GUI,新建一个GUI文件，进入GUI开发环境，如图3和图4所示。

图3 GUI创建界面

第二步，使用界面设计编辑器进行界面设计。

分析界面所要实现的主要功能，使用GUI开发环境提供的一系列工具，制作出演示系统主界面。

图4 GUI开发环境

1)用户菜单设计。

用户菜单的创建可以通过菜单编辑器完成。根据需要设计出一级菜单(菜单条)和二级菜单，点击更多属性可设置、修改菜单的属性，如图5所示。

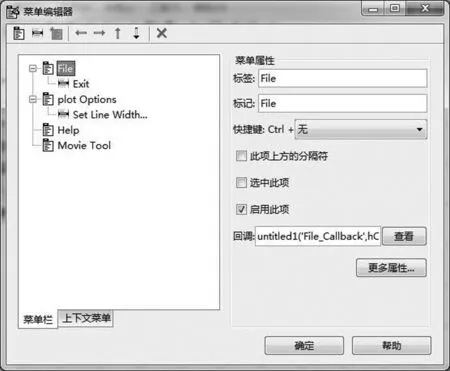
图5 GUI用户菜单设计界面

激活该图形用户界面，可得到如图6所示GUI用户菜单。

图6 GUI用户菜单

2)图形界面设计。

在布局编辑器中布置控件：本演示系统中使用了7个静态文本框(statictext)，分别用来完成显示不同信息的功能；2个滚动条(slider)，分别用来完成时域信号周期和傅里叶级数系数的选择；3个坐标轴(axes)，分别用来显示时域波形及频谱图；一个弹出式菜单(popupmenu)，用来进行时域信号的选择；一个可编辑文本(edittext)，用来输入傅里叶级数系数。

使用位置调整工具(alignmenttool)对控件的位置进行调整；使用对象属性查看器(propertyinspector)查看/修改设置各对象属性，如图7所示。

图7 GUI图形界面设计

上述步骤基本完成了图形界面的设计，保存并激活GUI，GUI界面布置如图8所示。

图8 GUI图形界面

第三步，编写控件行为响应控制(即回调函数)代码。

根据设计好的图形界面的功能，针对各个不同图形对象编写能够实现该功能的回调函数，通过控件响应指定行为。GUIDE给添加到应用程序fouriergui_callbacks.m文件中的回调函数自动命名，可直接用这个框架编写函数代码，并使控件被激活时该函数能够调用。

回调函数的声明为：

functionobject_CreateFcn(hObject,eventdata,handles)

其中:object为发生事件的控件的Tag属性字符串；hObject为发生事件的控件的句柄；eventData为保留字段；handles为一个结构体，这个结构中包含所有界面上控件的Tag属性值，还可以添加用户自己的数据。

回调函数编写主要是通过get、set语句对控件的属性进行获取和设置，以及完成相关数据的传递、保存和获取。

所有控件布置好后，可以激活按钮检查GUIDE的设计结果，激活时将保存fouriergui_callbacks.fig和fouriergui_callbacks.m文件。

最后激活的图形用户界面是对周期方波信号的分解与合成，如图9所示。

图9 周期方波信号的分解与合成

2.3 系统性能分析

可选择不同的信号类型实现时域波形显示及对应的幅频特性和相频特性的显示。可以通过鼠标拖动改变时域信号的周期，能同步地观察到时域参数改变后对应幅频特性和相频特性的改变。可以通过键盘输入或者鼠标拖动进行傅里叶级数系数选择，可以同时观察信号的合成与分解，还可以同时与理论值进行比较，观察吉伯斯现象。

3 结束语

本文从周期信号的傅里叶级数展开出发，结合周期信号分解与合成、频谱分析和吉伯斯现象三个重要知识点，对信号与系统课程中抽象概念的可视化方法进行探索。通过应用GUI编程技术设计出的图形用户界面，能够很方便地修改信号时域及频域的参数，将抽象的理论公式生动化，更加直观和形象具体地表现出来，该演示系统与理论教学和实验相结合，大大激发了学生的学习兴趣，改善了教学效果。

[1]孙明.《信号与系统》课程案例教学方法研究[J].武汉大学学报(理学版),2012(S2):173-176.

[2]李秀梅,董文,贾中云.基于Matlab的信号与系统课程GUI演示系统[J].大学教育,2014(9):78-79.

[3]陶亮.MATLAB图形用户界面在信号与系统课程教学中的应用[J].电气电子教学学报,2004,26(5):94-96.

[4]李念念,张红梅.基于MATLABGUI的信号与系统分析软件开发[J].工业控制计算机,2011,24(3):19-21.

[5]杜世民,杨润萍.基于MatlabGUI的“信号与系统”教学仿真平台开发[J].实验技术与管理,2012,29(3):87-90.

[6]金波.基于Matlab的“信号与系统”实验演示系统[J].实验技术与管理,2010,27(12):104-107.

[7]梁虹,梁洁.信号与系统分析及MATLAB实现[M].北京：电子工业出版社,2002.

[8]郑君里,应启珩,杨为理.信号与系统[M].2版.北京:高等教育出版社,2000．

[9]熊元新,刘涤尘.傅里叶级数的收敛性与吉伯斯现象[J].武汉大学学报(工学版),2001,34(1):69-71.

[10]于殿泓,李琳.“信号与系统”课程中的分解与合成[J].电气电子教学学报,2009,31(2):107-109.

[11]罗华飞.MATLABGUI设计学习手记[M].2版.北京：北京航空航天大学出版社,2011.

[12]陈垚光.精通MATLABGUI设计(附光盘)[M].北京：电子工业出版社,2008.