车辆仿生结构气动特性分析与优化

倪 捷，刘志强，秦洪懋，范秦寅

（1.江苏大学 汽车与交通工程学院，江苏 镇江 212013；2.清华大学 汽车安全与节能国家重点实验室，北京 100084；3.大阪大学 工学部，日本 大阪 5650871）

1 引言

车辆行驶过程中的空气动力学特性与其经济性、动力性和行驶稳定性等诸多性能有着密切的关系。研究表明[1]，车辆在高速行驶时，消耗燃油所产生的功率中，超过60%是用来克服空气阻力的。因此，在“节能减排”的国家需求下，对车辆气动升阻力特性进行合理且有效的优化，显得极为迫切和重要。

目前车辆空气动力学特性优化主要通过车身的流线形和局部改进等方法来实现[2-4]。由于这方面的研究日益成熟，降低阻力的空间愈来愈小，车辆减阻进入一个瓶颈期。近年来，利用工程仿生学理论设计的各种非光滑表面结构成为车辆减阻研究热点之一。文献[5-7]研究了凹坑非光滑表面结构对汽车气动性能的影响，指出行李舱盖，车身尾部和车身底部非光滑单元体的合理组合与布置具有减阻效果。文献[8]通过仿真研究了非光滑车身表面气动减阻的可行性，分析非光滑单元体的形状、大小以及分布位置和排列方式对减阻性能的影响。文献[1]研究了在轿车尾部增加功能类似中央鳍/对鳍的扰流板以及在车后窗及汽车后备箱表面添加形态仿生功能表面对车辆高速行驶状况下气动性能的影响规律。然而，利用仿生结构进行车辆气动减阻增稳，需要综合考虑仿生结构的形状、空间位置以及车辆行驶工况等方面的影响。

为此，采用CFD（ComputationalFluidDynamic）数值仿真的方法，基于多目标遗传算法（MOGA，Multi-objective Genetic Algorithm）研究在不同行驶工况下，带有不同沟槽型棱纹仿生结构的车辆空气动力学特性规律，获得仿生结构及其布置的最优方案，为车辆仿生学研究和工程应用提供理论依据和方法指导。

2 Ahmed车辆模型仿真与风洞试验

2.1 几何模型的建立

采用Ahmed车辆模型，该模型是研究车辆空气动力学的标准模型，其气动性能试验数据已有公开发表[9]。Ahmed模型后倾角选取为25°，进行1：1的几何建模，最终建立该车几何模型，如图1 所示。其总长、总宽和总高分别为 1．044m、0．389m 和 0．338m。

图1 原车几何模型Fig．1 Geometric Model of Original Car

2.2 计算模型与边界条件

根据车辆外流场仿真经验[10]，计算域取为长方体区域，长为15倍车长，其中出口距车身尾部10倍车长，宽为10倍车宽，高为5倍车高。在Hypermesh软件中对几何模型进行表面网格划分，然后将表面网格模型导入CFD软件SC/Tetra生成体网格，并在车身表面插入边界层网格，经多次网格优化和计算，使车身及轮胎表面Y+值介于（5～1000）之间。整个计算域网格数约为200万。

选用SST k-ω湍流模型，采用二阶迎风格式进行离散求解，计算域温度为常温，进行CFD稳态仿真计算。进口边界条件设为速度进口，其值设为车辆行驶速度；地面设为运动壁面，速度与车辆行驶速度保持一致；出口设为相对静压条件，其值为0；车身面设为无滑移面，其余壁面为自由滑移面。

2.3 仿真结果与试验验证

图2 风速为50m/s时Ahmed模型尾涡速度矢量对比图Fig．2 Comparison on Vortex Velocity Vector of Ahmed Model at the Wind Speed of 50m/s

为了验证仿真计算的精度，引用文献[9]中得到了Ahmed模型外流场及空气动力学特性试验结果，该试验风速分别为30m/s和50m/s。以风速为50m/s为例，图2给出了仿真和试验得到的距离车尾分别为0mm和200mm处尾涡速度矢量对比图。从图中可以发现，仿真得到的尾涡速度矢量分布与试验结果较为接近。进一步通过试验和仿真计算获得了该车模型在行驶速度为30m/s条件下的阻力系数CD和升力系数CL，如图3所示。由图可见，车辆阻力和升力系数计算误差均在5%以内。综上可知，建立的Ahmed车辆计算模型具有较好的精度。

图3 风速为30m/s下Ahmed车辆模型的升阻力系数对比Fig．3 Comparison on the Lift and Drag Coefficient of Ahmed Model at the Wind Speed of 30m/s

3 仿生结构的提出及优化方案

3.1 沟槽型棱纹仿生结构设计

目前，在车身表面采用的非光滑表面仿生结构大致有3种基本型式：半球形凹坑、半圆形沟槽、正三角形沟槽。选择正三角形沟槽仿生结构，在原车模型的后倾表面上设计棱纹仿生结构，如图4所示。以实现类似于涡流发生器的功能，其空气动力学原理是提前将层流转捩为湍流，以期延迟气流的分离。为了达到对边界层内空气运动的干扰，必须综合考虑仿生结构的分布位置以及运行车速的影响，确保仿生结构尺寸在更宽的车速范围内均能控制在边界层厚度范围内。

设定车速范围为（2～33）m/s，后倾面长度为222mm。因此，根据平板层流边界层的厚度计算公式[11]，可以计算得到该车边界层厚度最小为4mm。故设计的正三角形沟槽高度H必须控制在4mm以内。同时，设定相邻沟槽间的距离L范围为（0～5）L1，其中L1为正三角形的边长。

图4 棱纹仿生结构设计Fig．4 Ribbed Bionic Structure Design

3.2 仿生结构的优化分析

影响车辆空气动力学性能的因素很多，诸如车身流线、结构及位置，同时与行驶速度有着密切的关系。因此，引入棱纹仿生结构进行车辆气动减阻增稳，必须综合考虑仿生结构的几何形状、空间位置以及车辆行驶工况等。

以阻力系数CD和升力系数CL为优化设计目标函数，以仿生结构的几何尺寸H，空间布置尺寸L，以及行驶车速V作为设计变量，进行基于MOGA的带有棱纹仿生结构的Ahmed车辆模型优化分析，其计算流程，如图5所示。

图5 优化设计流程图Fig．5 Flowchart of Optimization Design

（1）确定设计变量数N为3，各自的取值范围如下：H=（1～4）mm；L=（0～23）mm；V=（2～33）m/s。

（2）采用拉丁方设计方法，同时为保证采样数目满足最少取样原则（Smin=（N+1）（N+2）/2）。故选择采样数 S为 20，最终的采样方案，如表1所示。

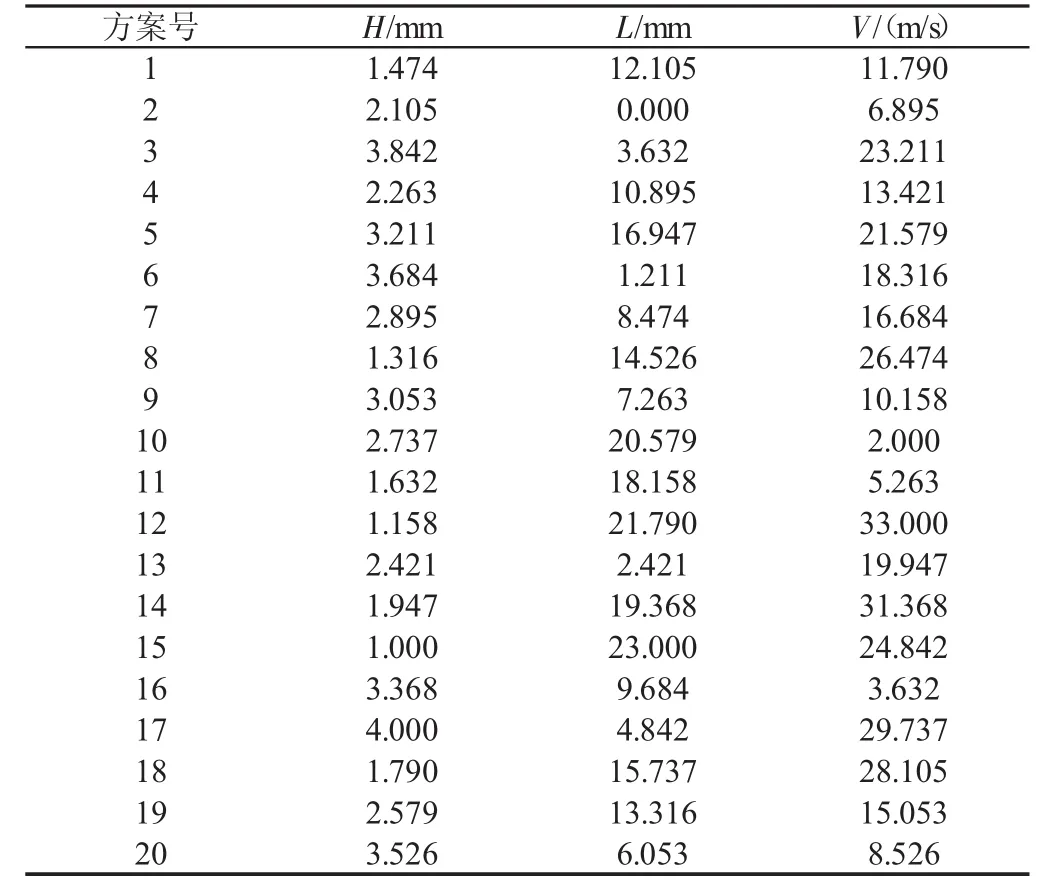
表1 采样计算方案Tab.1 Sampling Computational Cases

（3）采样方案的CFD计算及后处理：在进行带有仿生结构的车辆几何模型网格划分时，采用与原车计算时相同的计算领域和网格处理规范，对于车尾处仿生结构进行网格细化。同样经多次网格优化与CFD计算，保证整个车身及轮胎表面Y+值满足计算要求。每一个计算方案的网格规模控制在250万左右。利用商业CFD软件SC/Tetra的二次开发功能，笔者在EXCEL软件中编写VBA语言实现了每个计算方案的阻力系数CD和升力系数CL的自动化计算。

（4）Kriging近似模型的建立：气动外形设计优化过程需要多次调用参数化模型进行计算，直接采用高精度计算模型面临严峻的计算成本问题。因此，采用近似建模的方法替代复杂高精度实际性能分析模型是一种解决方案。常用于构建近似模型的方法有Kriging模型、径向基神经网络模型等。其中，全局近似的Kriging函数法（模型）以具有样本点处无偏估计、良好的高阶非线性拟合能力，近似面质量高等优点，在近似建模领域有着广泛的应用。该模型的具体数学表达形式在文献[12]中有详细的论述，不再赘述。

（5）MOGA算法的执行：由于涉及两个目标函数（阻力系数CD和升力系数CL）的最小值优化，属于多目标优化问题。对于多目标优化问题，各优化目标之间常常是相互联系制约的，因此一般不存在一个最优解使所有指标达到最优，而是通过求解得到由多个最优解组成的集合，称为Pareto最优解集[13]。由于个体可以并行地寻找多种解决方案，遗传算法被认为可能是最适合于多目标优化的计算方法。采用的MOGA算法，其基本思想是将优化问题可行域中的解看作种群（Generation）中的个体，并编译成编码符号串，对种群中的个体进行选择、交叉及变种操作，通过种群排序和拥挤距离计算，以适应度为依据，种群内的个体一代代进化，逐渐逼近最优解，最终可求出多目标优化问题Pareto最优解。

4 结果与分析

4.1 响应面云图

响应面分析法是利用一系列确定性的试验点，通过构造显式近似表达式，将涉及设计变量的目标与约束函数替代为显式函数关系，从而得到响应面模型来预测非试验点的响应值[14-15]。由于设计变量有三个（H，L和V），而目标函数为CD和CL，因此，响应面分布共有6张图来描述。限于篇幅，仅列出基于Kriging模型的目标函数-棱纹仿生结构参数的响应面云图，如图6所示。总的来看，棱纹仿生正三角形的高度H越大或相邻两个正三角形的距离L越小，阻力系数CD和升力系数CL都有增大的趋势，其中升力系数CL的变化规律更为复杂，有多个波峰和波谷的出现；阻力系数CD和升力系数CL的最小值点所对应的H和L区域是不一致的。

图6 基于Kriging模型的响应面云图Fig．6 Response Surface by the Kriging Model

4.2 贡献率

通过方差分析，各变量对目标函数的贡献率，如图7所示。由图7可知，对阻力系数贡献最大的是车速，而对于升力系数贡献最大的是相邻两个三角棱纹结构的间距。

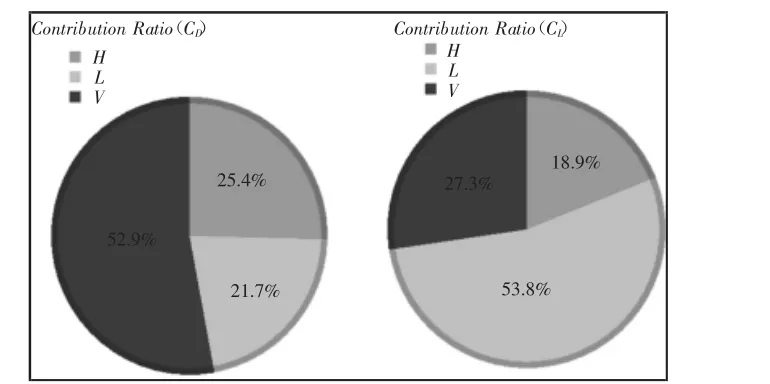
图7 各设计变量对目标函数的贡献率Fig．7 Distribution of Contribution to Object Function

4.3 Pareto最优解集

利用MOGA算法对目标函数进行迭代优化求解，设定种群数2048，初始进化代数为1，最终进化代数为1000，经过计算得到Pareto最优解集，如图8所示。由图可知，两个目标函数之间存在着十分明显的Trade-off关系，图中深蓝点所构成的外包络线即为可行解最优边界（Pareto Front）。很显然，该优化问题并无一个最优方案，需要从Pareto Front集中选择一个点作为最优方案。因此，由图可以发现，图中黑点所对应的解符合优化目标最小化期望，其CD和CL值分别为0．3098和0．2196，对应的棱纹仿生结构参数H和L分别为1．2032mm和21．2396mm，行驶速度V为32．8432m/s。

4.4 最优方案的验证计算

考虑到实际加工精度，对最优设计方案进行数据处理，确定棱纹仿生结构参数H和L分别为1.2mm和21.2mm。针对这一优化方案，在行驶车速为32.8m/s条件下分别进行理论和CFD验证计算。引入升阻力系数变化率指标，其计算公式如下：

式中：CX—阻力系数CD或是升力系数CL；CX0—未带有棱纹仿生结构的车辆阻力系数或升力系数。

有无形态仿生结构对升阻力系数的对比情况，如表2所示。由表可知，在高速行驶时，带有仿生形态结构的轿车阻力系数和升力系数都有明显的降低，其中升力系数的降幅最大，其变化率超过25%，极大地提高了车辆高速运行时运行稳定性。另一方面，从理论计算和CFD仿真计算的结果对比可知，构建的Kriging近似模型具有较好的预测精度，其预估精度在2%左右。

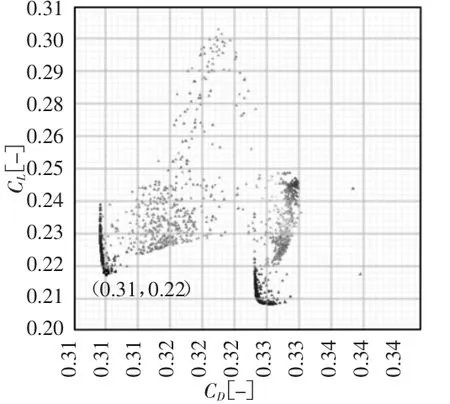
图8 Pareto最优解集Fig.8 The Distribution of Pareto Optimum Solution

表2 行驶速度为32.8m/s下阻力和升力系数变化率Tab.2 The Change Rate of the Lift and Drag Coefficient of Ahmed Model at the Wind Speed of 32.8m/s

5 结论

（1）在行驶速度为30m/s和50m/s条件下，对Ahmed车辆的空气动力学特性进行了数值模拟，并对比风洞试验结果可知，计算得到的尾涡速度矢量分布与试验结果较为接近，阻力和升力系数计算误差均在5%以内。

（2）在原车尾后倾面增加非光滑棱纹结构，以阻力系数CD和升力系数CL为优化设计目标函数，以仿生结构的几何尺寸H，空间布置尺寸L，以及行驶车速V作为设计变量，建立Kriging近似模型，并采用MOGA算法进行带有棱纹仿生结构的Ahmed车辆模型优化设计。

（3）经CFD验证，优化后的带有棱纹仿生结构的Ahmed车辆模型阻力系数降幅在5%左右，升力系数降幅约为29.35%，建立的Kriging近似模型的预测误差约为2%。

［1］田丽梅，商震，胡国梁.基于形态仿生的轿车升阻特性的数值模拟［J］.吉林大学学报：工学版，2014，44（5）：1283-1289.（Tian Li-mei，Shang Zhen，Hu Guo-liang.Numerical simulation of the lift and drag characteristics of passenger car based on morphological bionics［J］.Journal of Jilin University：Engineering and Technology Edition，2014，44（5）：1283-1289.）

［2］徐鹏，李春花，刘鹏.某SUV车型底部气动附件的开发与研究［J］.汽车技术，2014（7）：14-17.（Xu Peng，Li Chun-hua，Liu Peng.Development and research on pneumatic accessories on the bottom of A SUV［J］.Automobile Technology，2014（7）：14-17.）

［3］高静，杨志刚，李启良.基于近似模型的车身气动外形优化［J］.计算机辅助工程，2014，23（1）：1-6.（Gao Jing，Yang Zhi-gang，LI Qi-liang.Aerodynamic shape optimization and automotive body based on approximate model［J］.Computer Aided Engineering，2014，23（1）：1-6.）

［4］韦甘，杨志刚，李启良.不同造型风格的车身低阻基本形体［J］.计算机辅助工程，2014，23（3）：1-5.（Wei Gan，Yang Zhi-gang，Li Qi-liang.Low drag base bodies of different stylings［J］.Computer Aided Engineering，2014，23（3）：1-5.）

［5］杨易，聂云，徐永康.车身非光滑表面位置对气动性能的影响［J］.华中科技大学学报：自然科学版，2014（1）：23-27.（Yang Yi，Nie Yun，Xu Yong-kang.Influence of non-smooth surface decorated position effects on aerodynamic characteristic［J］.Journal of Huazhong University of Science and Technology：Natural Science Edition，2014（1）；23-27.）

［6］杨易，黄剑锋，聂云.车身单一非光滑表面与双表面耦合的减阻效果［J］.华中科技大学学报：自然科学版，2014（7）：124-127.（Yang Yi，Huang Jian-feng，Nie Yun.Drag reduction effect between single non-smooth surface and coupled double surface of motor［J］.Journal of Huazhong University of Science and Technology：Natural Science Edition，2014，（1）：124-127.）

［7］杨易，范光辉，聂云.基于SAE模型非光滑表面对气动减阻的影响［J］.机械科学与技术，2014，33（4）：559-563.（Yang Yi，Fan Guang-hui，Nie Yun.The influence of non-smooth surface effects on aerodynamic drag reduction based on SAE model［J］.Mechanical Science and Technology for Aerospace Engineering，2014，33（4）：559-563.）

［8］谌可，王耘，曹开元.仿生非光滑汽车表面的减阻分析［J］.中国机械工程，2012，23（8）：1001-1006.（Chen Ke，Wang Yun，Cao Kai-yuan.Analysis of aerodynamic drag reduction on automobile by using bionic non-smooth surface［J］.China Mechanical Engineering，2012，23（8）：1001-1006.）

［9］Hermann Lienhart，C.Stoots，Stefan Becker.Flow and turbulence structures in the Wake of a Simplified Car Model（Ahmed Modell）［J］.Notes on Numerical Fluid Mechanics（NNFM）：New Results in Numerical and Experimental Fluid Mechanics III，2002（.77）：323-330.

［10］张英朝.汽车空气动力学数值模拟技术［M］.北京：北京大学出版社，2011.（Zhang Ying-chao.Numerical Simulation Technology of Automobile Aerodynamics［M］.Beijing：Peking University Press，2011.）

［11］丁祖荣.流体力学［M］.北京：高等教育出版社，2013.（Ding Zu-rong.Fluid Mechanics［M］.Beijing：Higher Education Press，2013.）

［12］Shinkyu Jeong，Mitsuhiro Murayama，Kazuomi Yamamoto.Efficient optimization design method using kriging model［J］.Journal of Aircraft，2005，42（2）：413-420.

［13］Shinkyu Jeong，Kazuhisa Chiba，Shigeru Obayashi.Data mining for aerodynamic design space［J］.Journal of Aerospace Computing，Information and Communication，2005（2）：1-14.

［14］赵洁.机械可靠性分析的响应面法研究［D］.西安：西北工业大学，2006.（Zhao Jie.Study on response surface method for mechanical reliability analysis［D］.Xi’an：Northwestern Polytechnical University，2006.）

［15］Donald R.Jones，Matthias Schonlau，William J.Welch.Efficient global optimization of expensive black-box functions［J］.Journal of Global Optimization，1998，13（4）：455-492.