重量载荷对片层质量检测系统精度影响研究

甘 勇，莫宗杰

（桂林电子科技大学 机电工程学院，广西 桂林 541000）

1 引言

基于虚拟切片无损测量装置示意图，如图1所示。主要通过精密进给系统使被测物体平移至杠杆载物平台不同位置，再将不同测量位置下电子天平的质量去皮值代入平面力系平衡方程中，求解当前片层质量。再建立各片层质量与其所含微小单元体的方程组及重心坐标方程组，通过智能算法求解微小单元体的质量和空间坐标值，并通过对实体相应位置的质量与标准质量和周围质量比较，判断物体在检测范围内是否存在缺陷[1]。

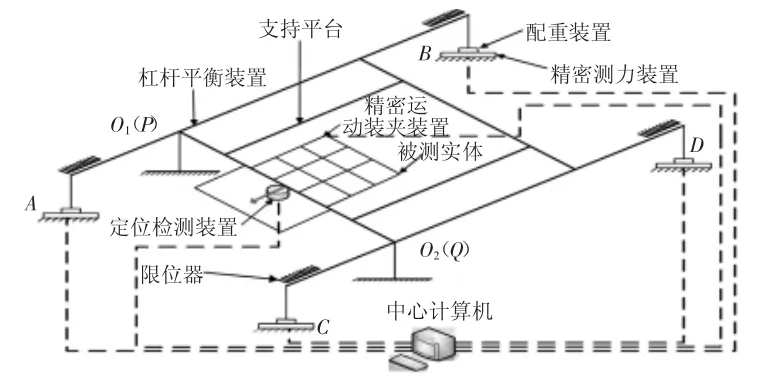
图1 基于虚拟切片无损测量装置示意图Fig.1 The Sketch Map of the Non-Destructive Measurement Device Based on Virtual Slice

基于虚拟切片无损测量装置具有测量精度高、成本低、数据测量与处理快、可测量物体内部轮廓等优点，改善了传统三维测量装置相关的不足。由于该装置最终需要通过求解微小单元体质量检测被测物体的内外部轮廓特征，而求解微小单元体过程需要建立各片层质量和所含微小单元体的方程组及重心坐标方程组，片层质量检测系统的精度将直接影响该装置最终测量精度[2]。而重量载荷作为片层质量精度主要影响因素，通过影响杠杆机构变形，改变杠杆机构力臂，从而引起片层质量计算误差。同时重量载荷范围大小也是衡量该装置实用性的重要标准，因此，可通过力学理论分析、有限元结构分析仿真，以及多重量载荷水平下片层质量误差分析等方法研究可行有效的误差补偿方法，以此降低重量载荷条件下，由力臂变量引起的片层质量误差，提高虚拟切片质量检测系统精度，以及优化基于虚拟切片无损测量方法。

2 重量载荷对片层质量检测系统结构可靠性影响分析

该装置最大重量载荷值由4各电子天平最大量程总和决定，单个电子天平最大量程为210g，则该装置最大重量载荷值为840g。由于承重导杆的横截面为矩形截面，根据材料力学弯曲轻度相关理论，计算装置正常工作条件下杠杆机构最大弯曲强度[3]，所涉及的相关公式如下：

式中：σmax—最大弯曲正应力强度；［σ］—许用弯曲应力；Mmax—最大弯矩；Wz—抗弯截面系数；E—弹性模量；rp—中性层最大曲率半径；Iz—惯性矩；bh—截面尺寸。

当载物平台移动至距离中点210mm处出现最大弯矩，假设被测物体为装置最大重量载荷值840g，经计算得到，作用与导杆上的集中力为8.232N，最大弯矩为1.7287N·m，抗弯截面系数为8.1667e-8，最大弯曲强度为21.1677MPa。该装置导杆材料为GCr15合金钢，需用弯曲应力为932MPa。最大弯曲强度小于许用弯曲应力，符合结构可靠性标准。经过ANSYS有限元软件可知，在满足测量装置最大重量载荷和最大弯曲强度的条件下，杠杆机构中导杆两端水平方向形变，即力臂变量分别为-0.1309mm和-0.0129mm，片层质量相对误差为0.0834，大于装置片层质量相对误差的设计值0.05。施加重量载荷条件下，由力臂变量引起的片层质量误差将直接影响微单元体质量精度，以及间接影响后期三维数据处理精度，因此，通过进行重量载荷对片层质量检测系统精度影响的分析，研究可行有效的误差补偿方法有助于提高该装置整体精度。

3 重量载荷对片层质量检测系统精度影响分析

运用ANSYS有限元软件仿真杠杆机构最大弯矩位置条件下，多水平重量载荷值对于导杆长度的影响，即片层质量计算公式中力臂LΔ1、LΔ2的变化。杠杆机构由支撑横梁、移动导轨、支撑座、滑块、挡块、载物平台6个部分组成，如图2所示。根据杠杆机构各零部件材料属性设置相关材料参数，主要材料属性参数，如表1所示。

图2 杠杆机构整体示意图Fig.2 Schematic Diagram of the Lever Mechanism

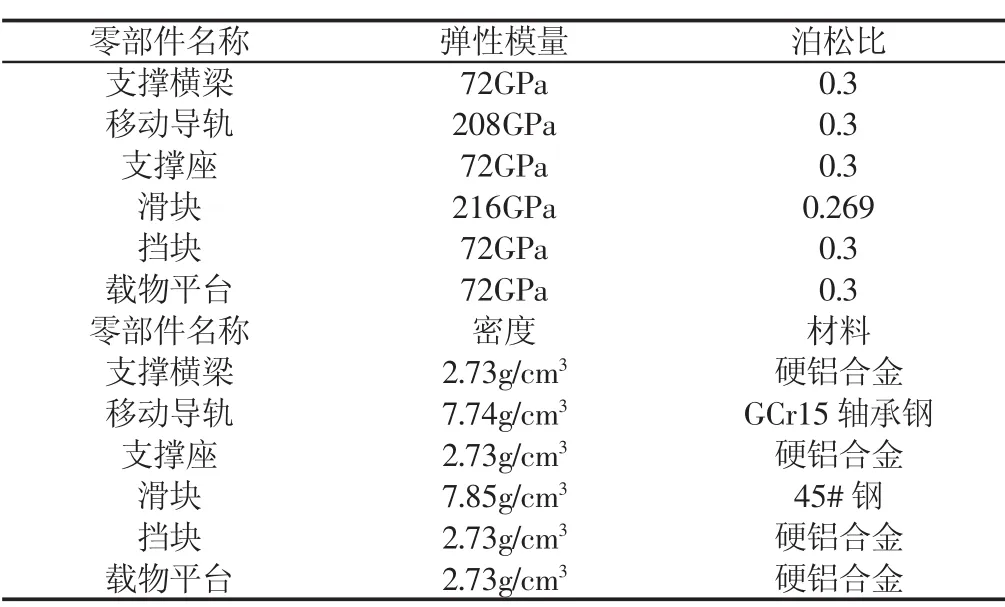
表1 杠杆机构材料参数表Tab.1 Material Parameters of Lever Mechanism

载荷边界条件设置如下，当载物平台处于最大弯矩位置条件下，仿真实验设置了6个位移约束（Displacement），分别是2个支撑块反面中间两斜槽面的2条相交线的X，Y，Z三个方向的全位移约束，如图2所示。以及左右两边两个支撑横梁上4个接触杆顶端在XZ方向上的位移约束。由于该装置的最大重量载荷值为840g，且作用于圆心位于载物平台正面几何中心上的半径为10mm的圆上，保证装置载物平台均匀分布向下的压力在此圆上。该装置杠杆机构ANSYS有限元软件网格划分与导杆方向位移，如图3所示。由图可见，杠杆机构网格划分较为合理，形状突变位置网格划分较为密集，整体网格密度适中，网格过渡平滑。共237307个节点，以及142135个网格单元体。载物平台移动偏向侧导杆端X方向的变形较为明显，可通过ANSYS中的Directional Deformation（方向性变形）功能检测导杆在水平方向上力臂的变化值，部分力臂变化分析，如表2所示。

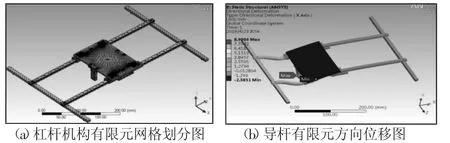
图3 杠杆机构变形分析图Fig.3 Deformation Analysis of Lever Mechanism

表2 重量载荷引起导杆力臂变量分析表Tab.2 The Load Caused by the Guide Rod Arm Variable Analysis Table

由表1可知，最大弯矩条件下，导杆两端力臂变量最大，并随着重量载荷降低，单向递减。运用ANSYS有限元软件仿真多水平重量载荷条件下导杆弹性变形，仿真分析出导杆弹性变形所导致杠杆机构力臂变化理论值[4]。力臂变化将直接影响片层质量计算精度，片层质量计算公式（第i片层）如下：

式中：x1i、x2i、x3i、x4i—4 个电子天平去皮值；L1、L2—左右两力臂值；Yi—当前被测片层质量；s—片层厚度；i—片层编码；G—被测零件总质量；xi—被测零件未测量部分重心；La1、La2—受重量载荷影响后力臂值；L1、L2—理论力臂值；LΔ1、LΔ2—力臂变量理论值。

由重量载荷引起的片层质量误差补偿推导公式如下：

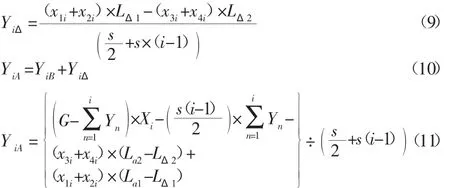
式中：YiA—误差补偿后片层质量计算值；YiB—误差补偿前片层

质量计算值；YiΔ—片层质量误差补偿值。

将ANSYS有限元软件计算的力臂变量、当前片层实际测量的去皮数据、以及片层厚度和片层编码代入该误差补偿公式中，即可计算出由重量载荷引起的片层质量误差的补偿值，误差补偿后的片层质量应等于理论计算值与误差补偿值之和，以此消除施加重量载荷条件下，由力臂变量引起的片层质量误差。

4 片层质量检测系统误差补偿分析与验证

片层质量误差补偿验证实验主要参数设置如下：测量范围为（0～210）mm，片层厚度为 0．2mm，进给速度 10 脉冲每秒，单位脉冲位移量为0．002mm，电子齿数比为8192/2500，数据收集间隔时间为9s，重量载荷初始水平100g，以50g等差递增，最大重量载荷840g。每组实验重复测量3次，取每个测量位置3次片层质量计算的平均值，误差补偿前后对比实验片层质量样本共计100800个，保证对比实验分析结果具有可靠性和可重复性。对比验证实验装置以及MATLAB片层质量计算及误差分析软件，如图3、图4所示。基于虚拟切片无损测量装置通过精密进给系统控制测量片层位置，并通过MATLAB片层质量计算及误差分析软件存储精密电子天平数据，通过智能算法计算片层质量，最后将片层质量测量值与理论值进行比较，分析相对误差、标准方差等数据分析度量。相对误差指的是测量所造成的绝对误差与被测量真值之比，与绝对误差相比，其更能反映测量的可信程度；标准方差是各数据偏离平均数的距离（离均差）的平均数，它是离差平方和平均后的方根，能反映一个数据集的离散程度[5-6]。通过数据分析度量能更直观的表现片层质量误差优化效果[7]。部分误差补偿验证实验分析结果[8-9]，如表2所示。

图4 基于虚拟切片无损测量装置实物图Fig．4 Entity Graph of the Non-Destructive Measurement Device Based on Virtual Slice

图5 MATLAB片层质量计算及误差分析软件界面Fig．5 MATLAB Slice Quality Solution and Error Analysis Interface

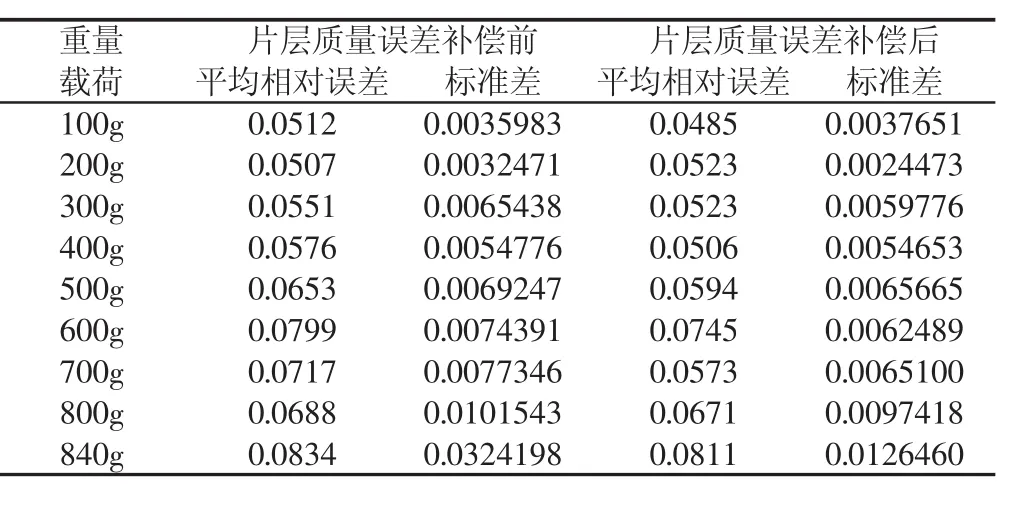
表3 片层质量误差补偿前后对比实验结果统计表Tab.3 Table Before and After the Error Compensation of the Film Quality Comparison Test Results Statistics

杠杆机构中导杆的弹性变形随着重量载荷的增加而递增，片层质量相对误差平均值和误差离散程度也随之增加，但由于影响片层质量测量精度的因素是多样的，因此少量片层质量误差补偿效果不佳，经过该误差补偿方法作用后，不同重量载荷下各位置片层质量相对误差总体上实现降低，片层质量相对误差降低成功率为 93．78%，相对误差平均值由 0．0649 优化至 0．0593，标准方差皆小于0．02，实现测量精度的提高和误差离散程度的降低。

5 结论

综上所述，在装置最大载重量程以内，杠杆机构弯曲变形小于其材料许用应力，未引起塑性变形，但经过片层质量计算推导过程与工程力学有限元分析，重量载荷也对片层质量精度造成影响；经过量化重量载荷对虚拟切片质量精度影响的分析，推导出相关的误差补偿公式，并通过误差补偿前后对比验证实验证明了该误差补偿方法的可行性，最终实现虚拟片层质量检测系统精度的优化，有助于基于虚拟切片无损测量方法的深化研究。但片层质量相对误差仍然未达到系统设计误差的目标，因此，下一步应进行针对其他精度影响因素的误差补偿研究。

［1］甘勇．基于静力平衡原理的三维均质实体测量方法［J］．中国机械工程，2012（11）：1350-1353．（Gan Yong．3D measurement method for homogeneous entity based on static balance principle［J］．China Mechanical Engineering，2012（11）：1350-1353．）

［2］甘勇，张福治，李玉刚．虚拟切片无损测量装置控制系统的研究［J］．机械设计与制造，2014（6）：140-142．（Gan Yong，Zhang Fu-zhi，Li Yu-gang．Research of virtual slice non-destructive measurement device control system［J］．Machinery Design&Manufacture，2014（6）：140-142．）

［3］唐进元，周长江，吴运新．齿轮弯曲强度有限元分析精确建模的探讨［J］．机械科学与技术，2004（10）：1146-1149+1248．（Tang Jin-yuan，Zhou Chang-jiang，Wu Yun-xin．Finite element analysis for bending strength of gear accurate modeling of［J］．Mechanical Science and Technology，2004（10）：1146-1149+1248．）

［4］王从晶，夏利娟．全船有限元结构分析的若干关键技术［J］．上海交通大学学报，2010（6）：768-773．（Wang Cong-jing，Xia Li-juan．Some key technologies of［J］．analysis of the finite element structure of Journal of Shanghai Jiaoyong University，2010（6）：768-773．）

［5］张福治．基于虚拟切片无损测量装置精密控制系统的研究［D］．桂林：桂林电子科技大学，2014．（Zhang Fu-zhi．Research on accurate control system of non-destructive measurement device based on virtual slice［D］．Guilin：Guilin University of Electronic Technology，2014．）

［6］陈阳．基于虚拟切片的三维无损测量装置系统误差分析与研究［D］．桂林：桂林电子科技大学，2015．（Chen Yang．Error Analysis and research of system of 3D nondestructive measurement device on virtual slide［D］．Guilin：Guilin University of Electronic Technology，2015．）

［7］刘焕牢．数控机床几何误差测量及误差补偿技术的研究［D］．武汉：华中科技大学，2005．（Liu Huan-lao．Research on geometric error measurement and error compensation technology of NC machine tool［D］．Wuhan：Huazhong University of Science and Technology，2005．）

［8］郭前建，赵国勇，程祥．双转台五轴机床空间误差补偿技术研究［J］．机械工程学报，2016（4）：1-6．（Guo Qian-jian，Zhao Guo-yong，Cheng Xiang．Research on spatial error compensation technology for five axis machine tool of double turntable［J］．Journal of Mechanical Engineering，2016（4）：1-6．）

［9］温正．精通MATLAB科学计算［M］．北京：清华大学出版社，2015．（Wen Zheng．Proficient in MATLAB Scientific Computing［M］．Beijing：Tsinghua University Press，2015．）