TC4钛合金微孔加工钻削力的仿真与试验研究
王凯旋,董志国,轧 刚,刘建成
(1.太原理工大学 精密加工山西省重点实验室,山西 太原 030024;2.美国太平洋大学,斯托克顿CA95211)
1 引言
随着现代工业的发展,产品小型化、精密化逐步成为制造业发展的趋势之一。微钻削因为其高效率、高精度等特性,在微孔加工中具有独特的优势。TC4钛合金由于强度大、生物兼容性好等性能,被广泛应用于航空、医疗等领域。然而TC4钛合金,作为一种难加工材料,使得在微细加工过程中,钻头十分容易磨损和折断。钻削力是影响微小钻头折断的主要因素[1]。通过监测轴向力可以对钻头的折断进行预测[2],为加工参数的优化提供依据。因此,对微钻削过程中钻削力进行研究具有十分重要的意义。
在传统钻削方面,研究人员已经采用了各种解析模型和数字模型来分析预测扭矩和轴向力。文献[3]采用解析法,将钻头主切削刃和横刃分别分解成一系列三维斜角切削单元和二维直角切削单元,都采用等效平面法解出每个单元的所受的力,然后再经过坐标变换求出整个钻头的轴向力和扭矩。文献[4]用UG建立钻头的模型,导入Deform软件进行钻头轴向力和扭矩的仿真。文献[5]了钻头主切削刃上每一个离散单元的切屑流角和切削力。文献[6]提出了斜角切削力模型,用等效平面方法把不等分剪切区的直角切削理论延伸并应用于斜角切削中,使用坐标变换方法分析了斜角切削几何参数之间的关系。
主要建立一种能够预测微钻削过程中钻头所受的切削力的模型。首先将钻头的主刃和横刃分别离散成一系列的斜角切削单元和直角切削单元,研究钻头在钻削过程中的受力;其次,用Deform软件进行斜角切削与正交切削的仿真,得到每个切削单元所受的力,在仿真过程中特别考虑刀刃钝圆半径的影响;然后将每个切削单元的力叠加,得出整个钻头所受的力;最后,进行多组工艺参数的仿真与试验,来验证该模型的正确性。
2 钻头切削力的解析模型
2.1 钻头的受力分析
钻头受力模型,如图1所示。将所采用的φ0.1mm钻头的主切削刃和横刃分别离散成五个斜角切削单元和两个直角切削单元;其中x、y、z是建立在整个钻头上的坐标分别为主切削刃和横刃在全局坐标系下所受的切向力、径向力、轴向力,(FC,FV,FT)分别代表切削单元所受的主切削力,竖直方向力,侧向力。
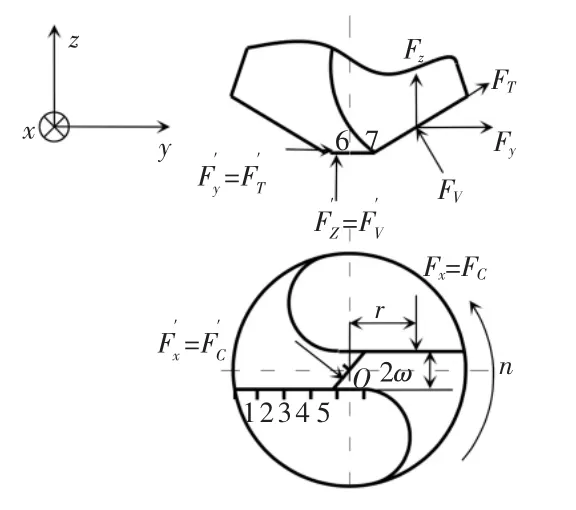
图1 钻头受力模型Fig.1 Forced Model of Drill Bit
2.2 微钻头切削的切削刃
通过KeyenceVHX-2000E显微镜测得各个切削单元的几何角度以及各个切削单元中心到钻头中心的距离,如表1、表2所示。由于端面刃倾角不同,针对单元(1~5)进行斜角切削仿真,单元6进行直角切削仿真。

表 1各个切削单元的几何角度Tab.1 The Geometric Angle of Cutting Unit

表2 各个切削单元中心到钻头中心的距离Tab.2 The Distance From the Center of Every Cutting Unit to the Center of the Drill Bit
2.3 钻削力的解析式
由于钻头的径向力相互抵消,只需考虑轴向力,和切向力。参考如图1所示,将每个切削单元的受力转换为整个钻头的受力的方程:


式中:Ttotal—钻头所受总的扭矩;
Fthrust—钻头所受总的轴向力。
3 微钻削有限元仿真
3.1 仿真步骤与参数设置
因为主要研究钻头横刃和主切削刃均参加切削时所受钻削力的平均值。所以,采用两个仿真步骤:(1)先采用Lagrangian分析步进行分析;(2)等到有切屑产生时,采用稳态加工解析进行分析。这样可以更加可靠的模拟出比较稳定的切削力。为了能够准确模拟出每个切削单元所受的切削力,每个切削单元被设为塑性类型,被赋予的材料是高强度硬质合金。刀具和工件网格划分均采用绝对类型,钻头size radio为2,最小单元为0.1mm,工件网格为size radio 7,最小单元尺寸为每齿进给量一半。在定义工件与刀具前刀面的导热系数为45N/sec/mm/C,摩擦系数为0.6,摩擦类型为剪切摩擦。断裂准则采用延伸断裂准则,根据材料的最大破坏值是否达到临界值来判断材料的断裂与否。
3.2 切削仿真的参数
以fz=0.0005mm/z,n=20000r/min为例来分析各个切削单元的仿真结果。切削过程中其他相关参数,如表3所示。

表3 切削过程中其他相关参数Tab.3 Other Relevant Parameters During Cutting
3.3 有限元仿真结果与分析
单元(1~5)和单元6的等效应力,如图2、图3所示。由云图可知最大应力出现在第一变形区。在单元(1~5)的斜角切削中,可以反映出,切屑流出方向相对于切削刃的法向偏斜一个角度,称为流屑角,并且端面刃倾角越大,流屑角越大。从图3的切屑成形过程,可以从本质说明上金属切削过程,即被切削金属层在刀具切削刃和前刀面的作用下,经受挤压而产生剪切滑移变。下面以切削单元3的受力为例,如图4所示。可知:切削单元的各个方向的受力先增大,然后稳定。进行受力分析时,只取受力比较稳定时的数据,用matlab求取平均值。进而得到每个单元的受力情况。


图2 斜角切削等效应力云图Fig.2 Oblique Cutting Yon Mises Nephogram

图3 直角切削等效应力云图Fig.3 Orthogonal Cutting Yon Mises Nephogram
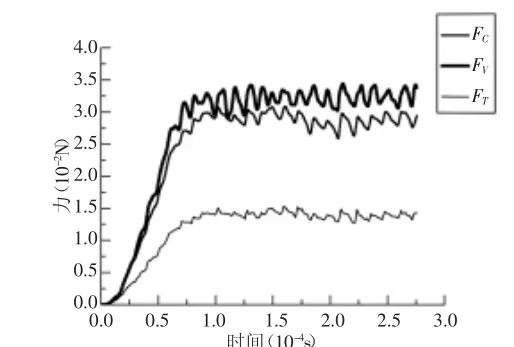
图4 切削单元3的受力图Fig.4 Forced Diagram of Cutting Unit 3

图5 切削单元均值载荷图Fig.5 Average Load Diagram of Cutting Unit
从上图中可以看到,单元1到单元5,每个切削单元所受的主切削力逐渐减小,侧向力和竖直方向的力逐渐增大。横刃单元的竖直方向的力以及主切削力急剧增大,这是由于钻头加工过程中,横刃切削条件非常不利,产生很大的轴向力的结果。另外也观察到每个单元的竖直方向的受力和主切削力大小相当,这主要是因为微细加工中,未切削层厚度与钝圆半径比值仅为0.5,产生明显的尺寸效应,即除了剪切力和塑性变形外,犁切力和弹性变形也是切削力的重要来源。将图5各个数据带人式(1)~式(6)进而可以求出钻头所受的扭矩和轴向力。
4 切削参数对钻削力的影响试验
4.1 微钻削的试验装置与切削参数
采用的哈斯机床以及Kistler 9129AA2型测力仪测得不同工艺参数下的切削力,如图6所示。对扭矩和轴向力产生影响的切削参数主要包括每齿进给量、钻头转速。由进给量经验公式:fz=0.0005mm、0.001mm时,犁切力和剪切力达到比较好的契合[8]。

图 6微孔钻削实验系统Fig.6 Micro Hole Drilling Experiment System

表4 钻削工艺参数Tab.4 Drilling Process Parameters
4.2 试验结果与分析
采用表4的工艺参数,得到图7、图8的仿真与试验结果,实线为试验结果,虚线为仿真结果。从图7可以得到,当fz=0.0005mm/rev时,转速n从20000r/min增大到50000r/min的过程中:扭矩仿真值从7.7022×10-3N.mm减小到4.3258×10-3N.mm,减小了43.84%,轴向力仿真值从1.4231N增加到1.5375N,增加了18.69%;扭矩试验值从8.96×10-3N.mm减小到4.87×10-3N.mm,减小了45.65%,轴向力试验值从1.4259N增加到1.7878N,增加了20.24%。从图8可以得到,当fz=0.001mm/rev时,随着转速n从20000r/min增大到50000r/min的过程中:扭矩仿真值从11.1386×10-3N.mm减小到5.7835×10-3N.mm,减小了48.08%,轴向力仿真值从1.3198N增加到1.7266N,增加了24.05%;扭矩试验值从15.0522×10-3N.mm减小到6.4983×10-3N.mm,减小了56.83%,轴向力试验值从1.6813N增加到2.2251N,增加了32.34%。每齿进给量一定时,随着转速的增大,扭矩与轴向力的仿真结果与试验结果变化趋势基本一致。并且从图7、图8知:轴向力的仿真值与试验值的最大差值分别为0.2514N和0.51N,分别约为试验值的16%和25%;扭矩的仿真值与试验值的最大差值分别为1.58×10-3N.mm和3.9136×10-3N.mm,分别约为试验值的23%和16%。因此可以验证仿真结果是比较可信的,上述的力学模型比较适合微钻削加工。从图中可以看出相同的切削参数下,仿真结果比试验结果小,主要原因:(1)没有考虑副切削刃的影响,在钻削过程中,副切削刃会与已加工过的孔壁进行摩擦,这就可能导致扭矩与轴向力的增大。这是上述力学模型的一个缺陷,没有考虑副切削刃。(2)实际钻削过程是一个半封闭的过程,切屑不易排出,进而会造成十分恶劣的加工条件,容易使切削力变大。该力学模型是假设切屑可以完全排出,没有完全模拟实际加工条件。
另外,从图7、图8中可以看出:每齿进给量一定时,随着转速的增大,扭矩减小,轴向力增大。转矩减小的原因:TC4钛合金属于塑性材料,在加工塑性材料时,随着转速n的提高,切屑和前刀面的摩擦系数u明显下降;在加工塑性材料时,前刀面会产生积屑瘤,将使实际前角增大,从而使主切削力减小,进一步减小转矩。轴向力增大的原因:在每齿进给量一定的情况下,随着转速n的提高,钻头进给量会增大,轴向力会增加。

图7 fz=0.0005mm/revFig.7 fz=0.0005mm/rev

图8 fz=0.001mm/revFig.8 fz=0.001mm/rev
5 结论
通过研究表明:(1)比较仿真与实验结果知:将微细钻头的主切削刃和横刃分别离散成一系列斜角切削和直角切削,进行仿真,可以比较准确的预测微钻削力。(2)从切削单元受到的竖直方向的力接近甚至大于切削力可以验证微切削中的尺寸效应。(3)当每齿进给量一定时,轴向力和扭矩随着转速的增加都会增大。
[1]吴鲁淑,汤宏群.微小钻头的失效研究[J].机械设计与制造,2012(7):119-121.(Wu Lu-shu,Tang Hong-qun.Studyon failureof carbide micro-drills[J].Journal of Machinery Design&Manufacture,2012(7):119-121.)
[2]杨兆军,杨永海,贾庆祥.通过轴向力监测预报微钻头折断的研究[J].光学精密工程,2003,11(5):477-480.(Yang Zhao-jun,Yang Yong-mei,Jia Qing-xiang.Study on monitoring and prediction of micro broken drill bit by the axial force[J].Optics and Precision Engineering,2003,11(5):477-480.)
[3]Strenkowski J S,Hsieh C C,Shih A J.An analytical finite element technique for predicting thrust force and torque in drilling[J].International Journal of Machine Tools&Manufacture,2004,44(12):1413-1421.
[4]周利平,吴能章.基于Deform3D的钻削力仿真研究[J].工具技术,2007,41(4):50-53.(Zhou Li-ping,Wu Neng-zhang.Cutting force simulation based on Deform 3d[J].Journal of Tool Engineering,2007,41(4):50-53.)
[5]Armarego E J A,Cheng C Y.Drilling with flat rake face and conventional twist drills—I.Theoretical investigation[J].International Journal of Machine Tool Design&Research,1972,12(1):17–35.
[6]李炳林,王学林,胡于进.斜角切削的热力建模与仿真分析[J].中国机械工程,2010(20):2402-2408.(Li Bing-lin,Wang Xue-lin,Hu Yu-jin.Thermal modeling and simulation analysis of oblique cutting[J].China Mechanical Engineering,2010(20):2402-2408.)
[7]刘翔,董志国,轧刚.超声振动微孔钻削轴向力研究[J].现代制造工程,2015(11):93-98.(Liu Yang,Dong Zhi-guo,Ya Gang.Study on thrust force in ultrasonic assisted micro drilling [J].Modern Manufacturing Engineering,2015(11):93-98.)

