面向线缆路径规划的改进萤火虫算法研究

李春泉，胡宇威，尚玉玲，王弘扬

（桂林电子科技大学 机电工程学院，广西 桂林 541004）

1 引言

线缆布局设计是机电产品研发工作中的重要环节之一，也是比较繁重的工作任务之一[1]。合理的线缆布局可以提升产品性能并且缩短研发成本和周期。在传统的线缆布局中，布线人员凭借布线经验和手工测量进行布线，而随着线缆数量的增加以及布线环境的复杂化，该技术无法合理的对线缆路径进行整体规划。目前，虚拟环境下的线缆布局设计方法主要包括自动布局设计和计算机辅助人机交互式布局。与计算机辅助人机交互式布局相比，线缆自动布局设计可通过计算机软件，运用布线算法自动完成线缆路径的规划，具有更高的布线效率。

早在1961年，文献[2]提出了李氏算法，即迷宫算法，并以该算法对避障的最短路径进行求解。文献[3]提出了利用机器人路径规划技术并把细胞分裂法作为搜索算法进行管线自动布局设计。文献[4]为解决复杂环境中的线缆布局问题，提出了先通过随机路径图计算出初始路径，之后考虑布线环境的约束并对初始路径优化，最终取得了较好的计算效率。文献[5]以UG为开发平台，实现了三维环境下的线缆布局设计。文献[6]提出了一种利用障碍物轮廓扩展的方法进行线路搜索，并解决了主干路径中的“井”字问题。这些方法虽然可以用于解决一部分的实际问题，但由于线缆路径规划的复杂性，高效的线缆布局优化算法仍有待开发。

随着优化理论和工程实践的发展，新型的人工智能优化算法如人工鱼群算法、萤火虫算法、蝙蝠算法得以提出[7-9]，由于线缆布线环境较为复杂，具有搜索空间较大，多约束条件的特点，上述算法不能够很好的应用于线缆布线中。因此将新型的人工智能算法应用于线缆自动布局中，分析了新型人工智能算法在线缆自动布局中的特点，并设计了一种面向线缆路径规划的改进的萤火虫算法，最后对该算法的可行性和有效性进行了实例验证。

2 布线环境建模

采用栅格（grid）表示布线环境，可避免在处理障碍物边界中的复杂计算。然后将布线空间离散化，对不同的栅格赋予不同的值。

2.1 环境的离散化和障碍边界的处理

首先根据式（1）、式（2）确定栅格的粒度，以布线起点为原点建立坐标系，且终点处于坐标系内。然后将以设定的栅格粒度对布线环境离散化。

式中：Aobs—障碍物的面积；Atotal—总体面积；lgrid—栅格粒度步长；lmin—栅格最小粒度；lmax—栅格最大粒度。

在离散化的同时，对障碍边界进行处理：

（1）根据障碍物相对于起点的位置，得到障碍物的坐标边界。

（2）将不满一个栅格的障碍物，视为一个栅格。

（3）有凹陷部分的障碍物，凹陷部分和障碍部分应视为一个整体障碍物，避免局域死区。

2.2 模型的建立

路径规划的问题表述如下：在环境A内进行布线，将环境A投影到一个二维平面从而得到布线环境C，并把C分为一个个大小相同的方格，方格的边长为 lgrid。有障碍物 obsi，i=1，2，3，…，n，obsi表示第i个障碍物的大小，并将obsi映射到布线环境C内。避障空间，x表示布线环境中的某一点。路径规划就是在避障空间Cavo内从布线起点到布线终点找出一条较优的路径。在二维矩阵graph中，用如下函数来描述布线环境中的障碍分布情况：

式中：Pos（x）=1—x坐标处有障碍物；Pos（x）=0—x的坐标处无障

碍物，整个布线环境由 Pos（x）=0 以及 Pos（x）=1 所组成。

用图1，图2作为空间模型建立的一个示例：一个将实际工作环境投影到二维平面上的布线环境，如图1所示。其中圆形环表示布线起点；矩形环表示布线终点；黑色的区域表示布线环境中的障碍物；白色的区域表示布线环境中可进行布线的区域，即避障空间。用上述建模方法可以得到图2空间模型，其中圆形环表示线缆布线的起点；矩形环表示线缆布线终点；黑色的栅格为障碍栅格，表示布线环境中的障碍物；白色的栅格为可布线栅格，表示布线环境中可进行布线的区域。

图1 布线环境Fig.1 Wiring Environment

图2 空间模型1 Fig.2 Spatial Model 1

在二维矩阵graph中，graph（a，b）表示该栅格四个顶点的坐标分别为 x（a-1，b-1），x（a-1，b），x（a，b-1），x（a，b）。

3 萤火虫算法的基本思想

萤火虫算法（FA）是一种群体搜索的随机优化算法。每只萤火虫均朝向相对各自最亮的那只萤火虫方的向进行移动，最终所有个体移动到亮度最高的萤火虫的位置上。从数学角度对萤火虫算法的描述如下描述：Iij=Ij×e-γ*r1j（5）

式中：γ—光强吸收系数；Ij—第j只萤火虫的荧光亮度；Iij—第i

只萤火虫所感受到第j只萤火虫的荧光亮度；rij—第i只萤

火虫到第j萤火虫的距离。

式中：βj—最大吸引度，表示第j只萤火虫的吸引度；βij—第j只

萤火虫对第i只萤火的吸引度。

式中：扰动项（α×ε）—萤火虫的随机走动以此避免算法过早进入局部最优的状态，α的取值范围是［0，1］；ε—一个均匀分布的随机数向量。

4 线缆布线算法设计

4.1 萤火虫的坐标

对布线环境建模，得到一个（M×N）的graph矩阵，矩阵下标可以表示布线环境的任一点的位并且能检测该位置是否触碰障碍。

根据矩阵列数为N，令萤火虫的位置具有N个维度，即Xi=（xi1，xi2，xi3，…，xiN），xiN表示第 i只萤火虫在矩阵的第 N 列的行数。

4.2 改进的萤火虫算法（IFA）

由于萤火虫算法的原理可知，若初始群体分布不均匀，则算法的全局搜索能力不强，收敛速度较慢。随机产生初始群体的萤火虫算法容易进入局部最优。而通过混沌所具有的遍历性、随机性和非周期性等特点，可提高萤火虫算法中初始解的质量。

由文献[10]可知，logistic映射所得解的均匀性差于立方映射，因此采用立方映射对萤火虫进行初始化。且在布线模型中，存在障碍栅格，因此映射要在已排除障碍栅格的搜索环境下进行。若搜索环境第d维度上共有n个连续的障碍区间，则区间长度分别记为A1，A2，A3，…，An，且障碍区间距空间第d维度的下界越近，其下标越小。每个障碍区间靠近环境下界的区间边界记为lA1，lA2，lA3，…，lAn。同理，m 个连续的非障碍区间长度可分为 S1，S2，S3，…，Sm，有 lS1，lS2，lS3，…，lSm。

令Ld表示搜索环境d维度的下界，Ud表示搜索环境d维度的上界。所有障碍区间长度相加得到总障碍区间长度记为LA。则第 d 维的映射公式如下：

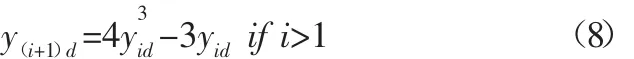
若第d维度上，不存在障碍区间，即n=0，则第d维度的映的射公式如下：

立方映射的实现过程如下：

Step1.有total只萤火虫在N维空间中，且随机生成一个N维向量代表第一只萤火虫的位置，Y1=（y11，y12，y13，…，y1N），且 y1j∈［0 1］，1≤j≤N。

Step2.进行total-1次迭代，得到其余萤火虫的位置。

Step3.将混沌的萤火虫位置按式（8）、式（9）、式（10）、式（11）映射到搜索环境中。

标准的萤火虫算法中，萤火虫通过相对亮度选择移动方向并进行移动，因此可能会导致荧光度最好的萤火虫向其他萤火虫移动。在移动后，该萤火虫的荧光度可能会比移动之前的荧光度差，从而在下一轮迭代过程中，萤火虫不能朝着一个较优的位置移动。

因此，在每一轮迭代过程中，筛选出荧光度最好的萤火虫，并令该萤火虫进行择优的移动，第d维度的位置更新公式如下：

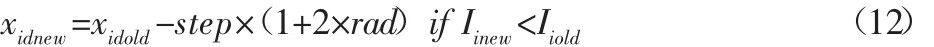
式中：Iinew—第i只萤火虫择优移动后的萤光度；Iiold—第i只萤火虫择优移动前的荧光度；M—布线环境处理中所得到矩阵的总行数；step—搜索步长，且step=M/10。

对荧光度较差的Num只萤火虫使用遗传算法的变异功能，且 Num=round（total/6）。

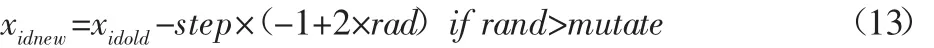
式中：mutate—变异概率，取值范围［0 1］；round（）—四舍五入的

取整函数；total—萤火虫的总个数。

其余萤火虫第d维的位置移动公式如下：

改进的萤火虫算法实现过程如下：

Step1.初始化算法基本参数。设置最大迭代次数或搜索精度；萤火虫数目；最大吸引度；光强吸收系数；步长因子；随机移动参数。

Step2.利用立方映射初始化种群得到total个初始解，并计算出所有萤火虫的荧光度。

Step3.对比萤火虫的荧光度，确定荧光度最好的萤火虫，根据相对荧光度以及萤火虫的相对吸引度确定其他萤火虫的移动方向。

Step4.根据式（12）更新荧光度最好的萤火虫位置，根据式（14）更新其余萤火虫位置，判断荧光度较差的萤火虫是否发生变异，若发生变异则转入Step5,否则转入Step6。

Step5.根据式（13），萤火虫发生变异。

Step6.根据更新后萤火虫的位置重新计算荧光度。

Step7.当计算结果满足精度或迭代次数达到最大时，则转Step8，否则转Step3，且迭代次数加1进行下一次迭代。

Step8.输出全局最优值和最优个体位置。

5 仿真结果

5.1 改进萤火虫算法（IFA）的仿真结果

选取了空间模型作为算法的测试用例，如图3所示。其中圆形环表示布线起点，矩形环表示布线终点，白色的栅格表示可布线栅格，黑色的栅格表示障碍物,且lgrid=1cm。

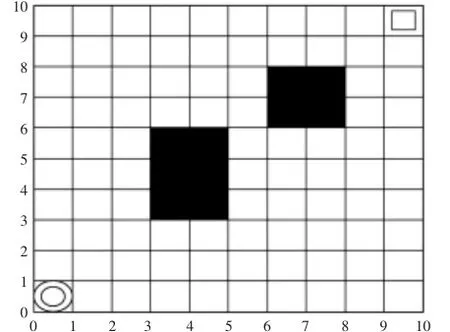
图3 空间模型2Fig.3 Spatial Model 2

算法的参数设置：萤火虫数total=20；光强吸收系数γ=1；最大吸引度βj=1；搜索步长step=1；随机移动参数α=2；迭代次数；mutate=0.4；iteration=200。将IFA运行50次，并把全部收敛曲线进行拟合所得到的趋势曲线，如图4所示。黑色箭头表示该算法计算出的线缆路径，如图5所示。

图4 IFA趋势曲线Fig.4 IFA Trend Curve

图5 线缆路径Fig.5 Cable Route

5.2 与其他人工智能算法的对比

把与测试用例中同样的布线环境用于IFA、基础的萤火虫算法（FA）、蝙蝠算法（BA）、人工鱼群算法（AFSA）和具有变异功能的粒子群算法（IPSO）运行50次且最大迭代次数为200，结果如表1所示。

表1 算法对比Tab.1 Comparison of Algorithms

由表1可知，所有算法运行50次时，IFA的最优值与平均值之差仅为0.2517cm，最优值与最差值之差仅1.1716cm，方差为仅为0.0973cm2，计算结果的波动幅度远优于IPSO、AFSA、FA，略差于BA。

AFSA、BA、IFA、IPSO、FA运行50次，如图6表示。并分别把每个算法的全部收敛曲线进行拟合所得到的趋势曲线。根据表1、图6可知，相比于IFA，BA和AFSA具有较快的收敛速度，但算法易处于局部最优的状态，因此求得的最优解误差较大，寻优率太低；IFA算法相比于表1中其他算法拥有较高的寻优率，算法的收敛速度与IPSO以及FA相近，算法程序每次执行后的最优解波动幅度较小。

图6 趋势曲线对比Fig.6 Comparison of Trend Curves

6 结语

对一种新型的人工智能算法-萤火虫算法进行了研究，同时针对标准萤火虫算法收敛速度较慢、易陷入局部最优等问题，提出了一种改进的萤火虫算法（IFA）并将其用于线缆路径的自动规划。该算法首先利用混沌映射初始化萤火虫位置，使萤火虫较为均匀分布在环境内；对精英的萤火虫采用择优移动的策略，保证萤火虫移动向较优的方向移动；对荧光度较差的个体进行变异增加了算法全局搜索能力的局部搜索能力，使算法不易陷入局部最优。最终，与各种人工智能算法对比，该改进算法在保证收敛速度的同时，提高了线缆路径的质量以及寻优率，验证了算法的可行性。

［1］刘潇，刘检华，刘佳顺.基与改进随机路径图的分支线缆自动布线技术［J］.计算机集成制造系统，2014，20（12）：2952-2961.（Liu Xiao，Liu Jian-hua，Liu Shun-jia.Multi-branch cable automatic routing based on improved PRM ［J］.Computer Integrated Manufacturing Systems，2014，20（12）：2952-2961.）

［2］Lee C Y.An algorithm for path connections and its application［J］.IRE Transactions on Electronic Computer，1961，10（3）：346-364.

［3］Zhu D，Latombe J C.Pipe routing-path planning（With many constraints）［C］.Proceedings IEEE International Conference on Robotics and Automation，1991：1940-1947.

［4］KABUL I，GAYLE R，MING C.Cable route planning in complex environment using constrained Sampling［C］.Proceedings of 2007 ACM on Solid and Physical Modeling.New York：ACM，2007：395-402.

［5］蔡毅，王彦伟，黄正东.基于UG的三维自动布线技术研究［J］.计算机工程与应用，2012，48（8）：68-72.（Cai Yi，Wang Yan-wei，Huang Zheng-dong.Research on 3D automatic electrical routing in UG system［J］.Computer Engineering and Applications，2012，48（8）：68-72.）

［6］李春泉，徐楚，张明.基于轮廓扩展方法的电气线缆布线技术研究［J］.机械设计与制造，2015（4）：266-269.（Li Chun-quan，Xu Chu，Zhang Ming.Routing technology of electric cables based on the method of contour extension［J］.Machinery Design&Manufacture，2005（4）：266-269.）

［7］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法［J］.系统工程理论于实践，2002，22（11）：32-38.（Li Xiao-lei，Shao Zhi-jiang，Qian Ji-xin.An optimizing method based on autonomous animals：fish-swarm algorithm ［J］.System Engineering Theory and Practice，2002，22（11）：32-38.）

［8］YANG X-S.Nature-in Spired Metaheuristic Algorithm［M］.Frome：Luniver Press，2008：81-96.

［9］X S Yang.A New Metaheuristic Bat-inspired Algorithm［M］.Berlin：Springer，2010：65-74.

［10］周燕，刘培玉，赵静.基与自适应惯性权重的混沌粒子群算法［J］.山东大学学报：理学版，2012，47（30）：1-6.（Zhou Yan，Liu Pei-yu，Zhao Jing.Chaos particle swarm optimization based on the adaptive inertia weight［J］.Journal of Shandong University，2012，47（30）：1-6.）