一种基于禁忌搜索算法的设站问题解决方案*

邱 恋，李秦伟

0 引 言

设站问题是网络规划过程中的关键问题，不仅影响用户的通信质量，而且影响运营商的运营利润。网络规划过程中的设站问题，实质是从多个候选基站中选择既满足通信质量要求又能使运营商设站成本最低的一组若干个基站。

1 通信网规划简介

通信网络规划的目标，是在要提供业务的区域里，根据所要保证的业务、所要支持的业务量、所需服务的用户数量，通过采用一系列理论分析、工具仿真与预测，获得支持相应用户数量所需的网络设备的数量、配置和部属地点[1]，以供核算网络投资，并为未来的工程设计提供参考。下面以WCDMA系统的网络规划为例进行说明。

无线网络规划是WCDMA系统走向商用的关键工作，直接影响网络建设成本、网络容量、服务质量以及设备性能的发挥。WCDMA无线网络规划的工作分为初步规划和详细规划两阶段[2]。初步规划的结果通常是对网络规模有一个数量上的认识，而基站站址选择则是详细规划的重要内容[3]。

通信网规划中，设站问题的关键主要有两个：一是所需站的数量，二是站点设置的位置。如何确定站点数量和站点对应设置位置，可归类为组合优化问题。

组合优化问题可以用一个包含三个参数的关系式表示即(D,F,f)，其中D表示决策变量的定义域，设站问题中相当于需要规划的区域；F表示可行解区域，设站问题中相当于候选站址集合，F中的任何一个元素称为该问题的可行解；f表示目标函数，设站问题中等同于满足基站建站成本和满足通信质量要求的代价函数。具体地，满足式（1）的可行解x*称为该问题的最优解。

可以看到，F的数量有限，只要有充足的时间对可行解集F的每一种情况进行尝试，总会找到满足f最小的解[4]。

在通信网规划过程中，站址选择的目标函数通常包括基站建站费用C、满足功率覆盖要求时基站位置折合成的代价D、移动台与基站连接需要的代价K以及连接基站中继线的代价X等，即目标函数L为：

设第i个基站的建站成本为fi，将第i个移动台与第j个基站连接的代价设为cij，再把D和X折算成每个基站的权重wi，则式（2）可写成式（3）：

式中dij表示第i个移动台与第j个基站的距离测度。此时的设站问题可描述为，在基站候选集F中，找到满足代价L最小时的一组k个基站和k个基站对应的位置f(d)。

对于一个中等规模的规划场景，假设有50个候选站址，则可选的规划方案可达250-1种。显然，这种问题通过穷举方法求得最优解是不可行的[3]。这类选择优化问题一般可用启发式算法求解，从可行解域中寻找一个在可接受的计算时间内能找到的可行解作为问题的解。

2 禁忌搜索概述

2.1 启发式算法简介

启发式算法是相对于优化算法提出的。它可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间、占用空间等）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度不一定事先可以预计[5]。

启发式算法包括禁忌搜索算法（Tabu search）、模拟退火算法（Simulated Annealing）、遗传算法（Genetic Algorithms）、神经网络算法（Neural Networks）和拉格朗日松弛算法等。这些算法涉及生物进化、人工智能、数学和物理科学、神经系统和统计力学等概念，是以一定的直观基础而构造的算法，故而称之为启发式算法。

2.2 禁忌搜索简介

禁忌搜索（Tabu Search或Taboo Search）[6]作为一种常用的优化算法，最大的优点在于可以跳出局部最优解，找到全局最优解[7]。一方面，算法通过设置禁忌表，把已经找到的一组准最优解放在禁忌表中保护。设置禁忌长度表示保护进行多少步。例如，禁忌长度设置为3，则接下来的3步被保护的准最优解将不被考虑。另一方面，算法还设置了一种特赦原则，即如果找到一组新的解，它的目标函数比之前已找到的所有情况都要好，那么这个新的最优解就作为当前为止的最佳解（best_so_far），同时将该解送入禁忌表进行保护。

禁忌搜索算法的主要过程是在邻域内寻找全局最优解[8]，是人工智能与局部邻域搜索算法的结合，沿袭了邻域搜索的邻域构造，并增加了一个禁忌表。值得关注的是，邻域的连通性是禁忌搜索可以达到全局优解的一个必要条件[9]，其连通与否直接关系禁忌搜索算法能否得到全局最优解。

禁忌搜索涉及到禁忌表（tabu list）、禁忌长度（tabu length）、邻域（neighborhood）、候选解（candidate）、特赦准则（free pardon criterion）等概念[10]。

2.3 禁忌搜索算法流程

邻域。在禁忌搜索算法中，邻域是一个相对于初始解的概念。假设算法的所有解集为C,给定的初始解为Zs的邻域为Ni,则应有：

且Z与Ni之间必须连通。

禁忌表。禁忌表用来保存当前搜索步数下被禁止考虑的解集。该解集元素的数量主要由禁忌长度决定。同时，若禁忌长度值为n，则也决定了被禁止考虑的某个解在接下来的n次搜索将不会被考虑。

候选解。候选解是从前一次搜索所使用的解的邻域中选出来的一组或若干组解，候选解一定不是禁忌表中的保护项。

特赦准则。特赦准则用于保存当前搜索次数为止得到的最优解。

简单禁忌搜索算法的基本思想：给定一个当前解（初始解）和一种邻域，在当前解的邻域中确定若干候选解；若候选解对应的目标值中有优于当前为止最佳解“best_so_far”状态的，则忽视其禁忌特性，用其替代当前解和“best_so_far”状态，并将相应的对象加入禁忌表，同时修改禁忌表中各对象的任期；若不存在上述候选解，则无视它与“best_so_far”的优劣，在候选解中选择非禁忌的最佳状态为新的当前解，同时将相应的对象加入禁忌表，并修改禁忌表中各对象的任期；如此重复上述迭代搜索过程，直至满足停止准则[11]。

算法步骤可描述如下：

（1）设置搜索参数，初始解设为z，并清空禁忌表。

（2）判断算法终止条件是否满足？若是，则结束算法并输出优化结果；否则，继续以下步骤。

（3）把当前解z作为邻域函数的输入参数调用邻域函数，从其所产生的z的邻域解集中确定若干候选解。

（4）候选解代入目标函数L，所得结果与特赦准则进行对比判定。若符合特赦准则，则用最佳状态y替代z成为新的当前解即z=y，并用与y对应的禁忌对象替换早进入禁忌表的禁忌对象，同时用y替换“best_so_far”状态，然后转步骤（2）；否则，进行步骤（5）。

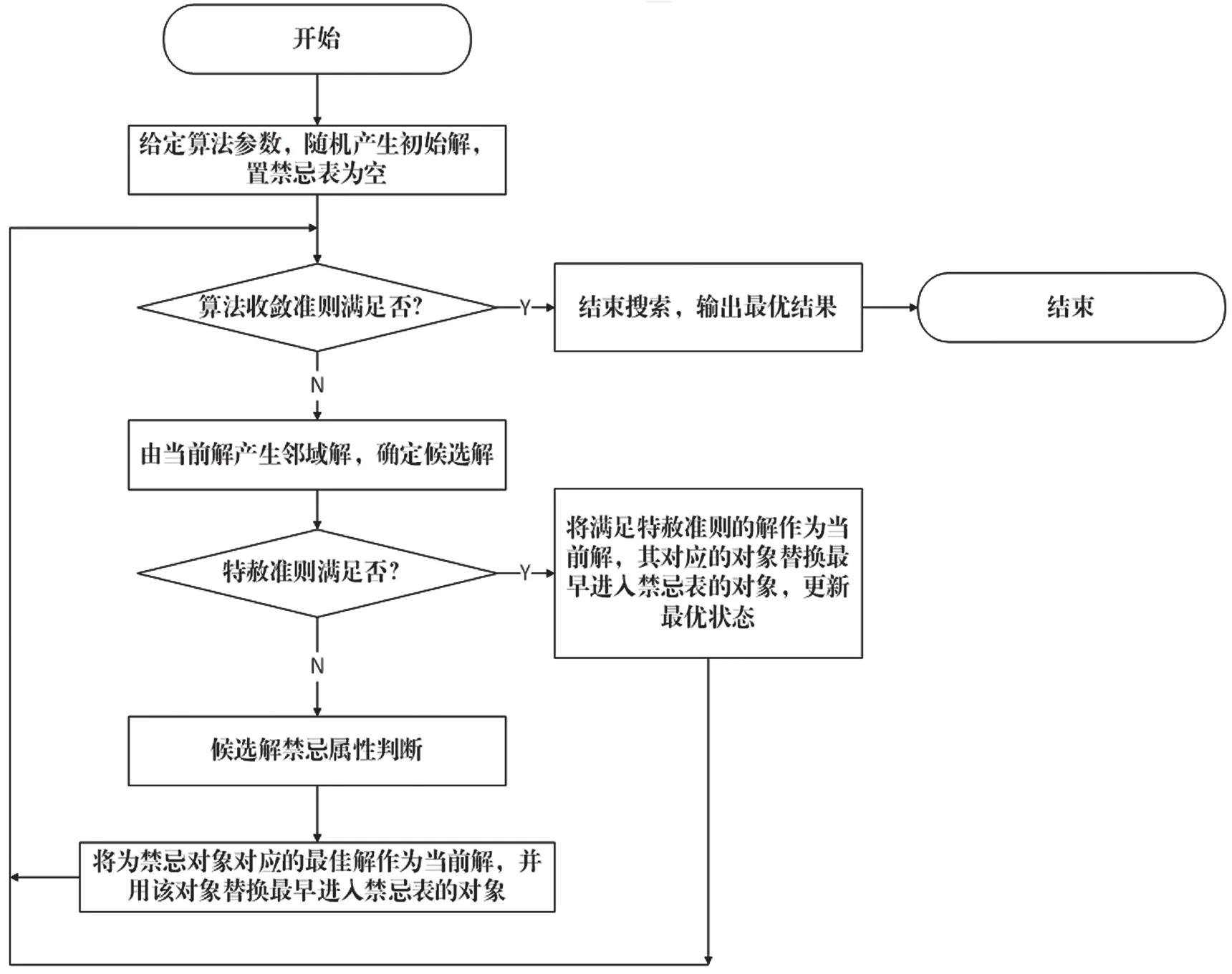
图1 算法流程

（5）判断候选解对应的各对象的禁忌属性，选择候选解集中非禁忌对象对应的最佳状态为新的当前解，同时用与之对应的禁忌对象替换早进入禁忌表的禁忌对象元素，转步骤（2）。

上述算法可用流程图更直观,描述，如图1所示[4]。

从算法流程可以看出，禁忌表、禁忌长度、邻域函数和特赦准则是禁忌搜索算法的关键。其中，禁忌表和禁忌长度的设置能为局部最优解提供保护；邻域函数沿用局部邻域搜索的思想，用于实现邻域搜索；特赦准则用于保护当前最佳解并保存全局最优。上述算法仅是一种简单的禁忌搜索框架，对各关键环节复杂和多样化的设计，它可构造出各种禁忌搜索算法。同时，算法流程中的禁忌对象可以是搜索状态，也可以是特定搜索操作，甚至是搜索目标值等。

3 算法设计与实验分析

3.1 案例与分析

本文假设在指定区域内，经前期预规划，确定30个候选基站位置，如图2所示。

30个候选基站的位置坐标表示成矩阵：

一天，宋娟的父亲从街上买回一个西瓜，那个西瓜的皮非常厚，母亲舍不得扔，就把外面的青皮一刨，切成一片片炒出了一盘美味的蔬菜。这给了宋娟一个大胆的想法：能不能把柚子也当成蔬菜卖？

设它们的相对建站费用分别为：

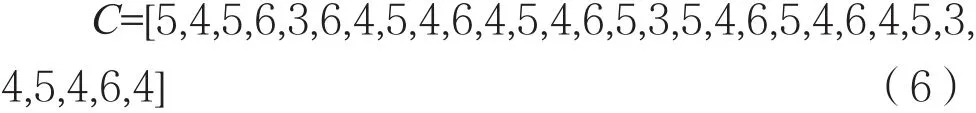
设在所规划的区域内移动台均匀分布，要实现完全覆盖预计需要10个台站。

实际问题中，为排除候选站址集中分布的不合理情况，需要把候选站址分组，以确保规划区域内台站的分散性。根据站点位置关系和离散程度，将候选站址区分为10个小组，通过穷举的方法，代入式（3）计算所有的310种组合，得到如图3所示的各种组合情况对应的规划代价值。

由图3可知，代价最小值Lmin=189 277.778 3，其对应的组合即为最优组合，同时也是本实例的最优解。

3.2 算法设计

3.2.1 邻域构造

本文设计了一种基于随机因子的邻域构造方法。邻域构造原理图如图4所示。

由初始解（或前一次搜索所使用的解）z和随机因子s共同确定初始解（或前一次搜索使用的解）的邻域。设解为 z=[z1,z2,…zi]，则对应的邻域N为：

实例中候选站址的数量是有限的。所以，随着si的多次随机跳变，可以遍历所有的组合情况，保证邻域的连通性。同时通过对si的设置，可以调整领域变化的强度。

3.2.2 搜索完成条件

设置完成搜索的条件有两个，一是禁忌搜索次数达到100次到达上限、停止搜索，并认可当前为止最佳“best_so_far”为最佳解；二是“best_so_far”状态保持连续40次不变且有15次回归“best_so_far”状态。此时，认可“best_so_far”值为最优站址方案时的最佳目标函数值，对应的站址方案为最优站址方案，同时结束搜索。

3.2.3 算法参数设置

本算法中设置一个禁忌表，禁忌长度为5。将式（3）作为设站问题的目标函数，初始解设置为Z=[2,6,9,12,15,16,20,24,27,30]，即案例中的第2、6、9、12、15、16、20、24、27和第30共10个基站位置作为初始解。

3.2.4 算法过程描述

由初始解Z出发，计算对应的目标函数值L。第一次搜索时，该L值直接作为“best_so_far”，同时Z进入禁忌表，并在接下来的5次搜索中不再考虑。

通过本文设计的邻域构造方法构造邻域，再从邻域中随机选定3组解（每组10个点）作为下一次搜索的候选解，并计算对应目标函数值L，取其中最小的L值作为本次搜索结果，同时与当前为止最佳状态“best_so_far”对比，确定是否更新“best_so_far”值，并更新禁忌表项和各表项对应的禁忌步长。

判断搜索完成条件是否满足。不满足，继续搜索；满足，则跳出搜索，记录“best_so_far”及对应的最优解。

3.3 结果分析

仿真过程中，共搜索60次，小于最大搜索次数100次，即满足搜索完成条件二仿真结束。“best_so_far”状态保持连续40次不变且有15次以上最佳状态回归，则认可该“best_so_far”状态为全局最优解，对应所得最优设站方案即为图5、图6，分别为当前为止最佳状态与各次搜索结果的对比关系图。

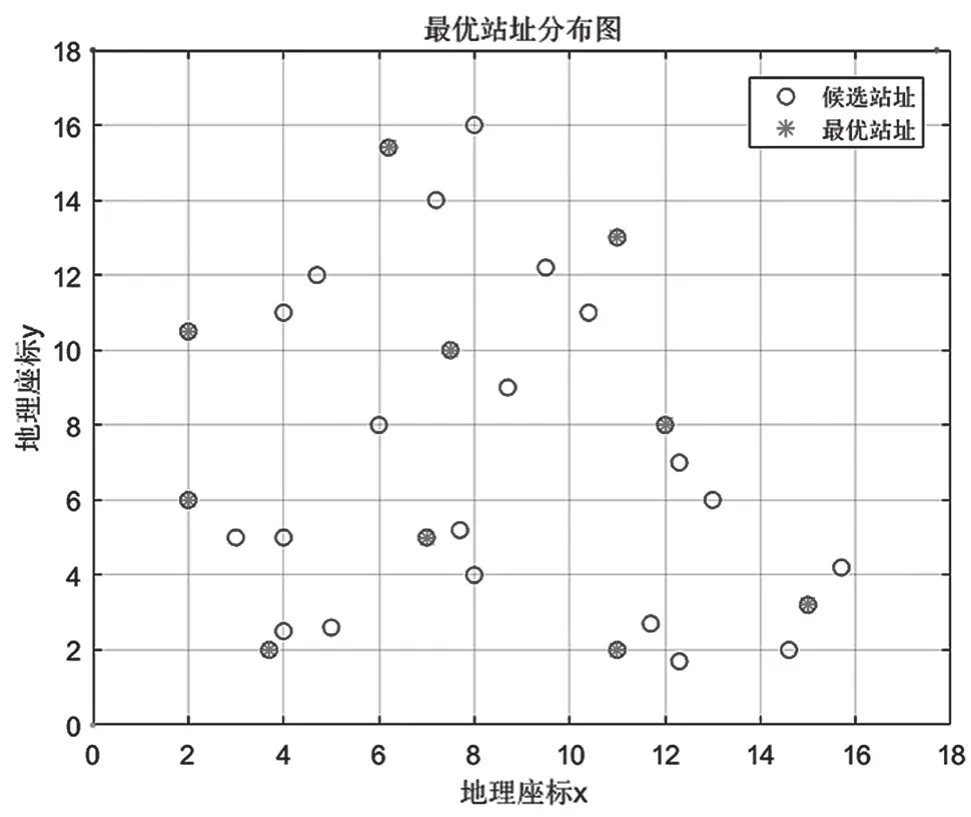
图5 最优站址分布情况

图5 中，“*”点即为当前案例的最优解。从图 5可 知， 选 择 第 1、4、7、10、13、16、21、22、27和第29个基站时，为最佳设站方案。

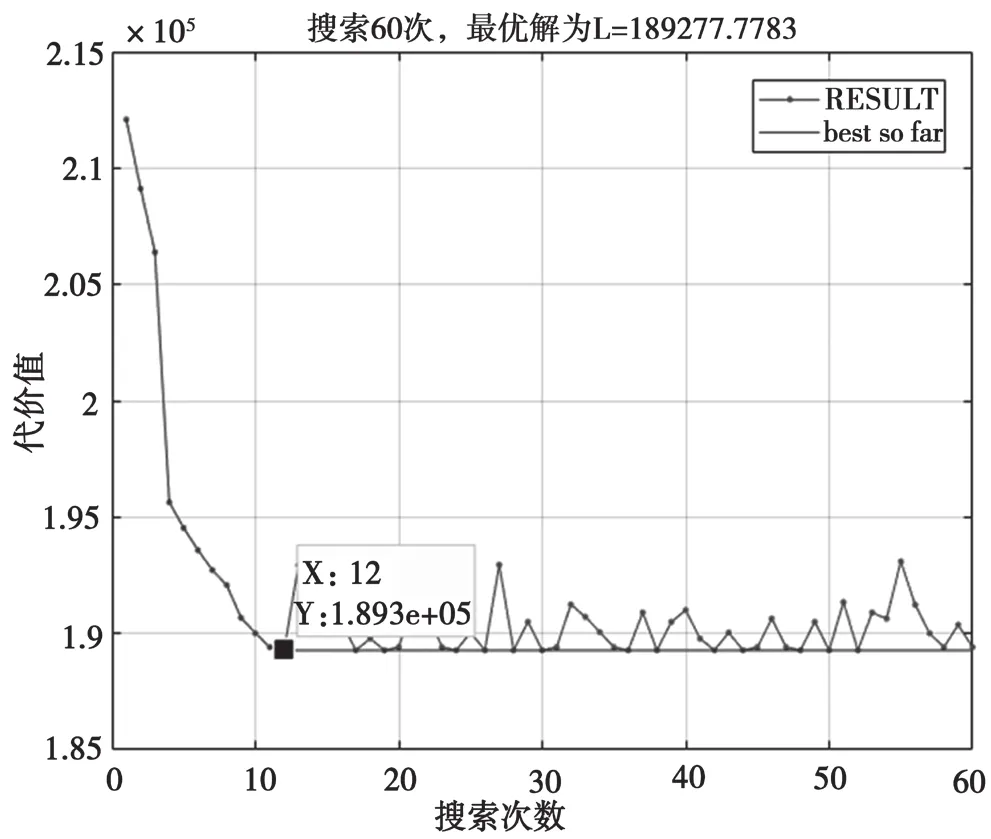
图6 局部最优与全局最优关系

图6 中加“.”的RESULT曲线表示每次搜索时得到的本次搜索目标函数值（局部最优），平滑“best_so_far”曲线则表示到当前搜索为止目标函数的最小值（全局最优）。从图6可知，当搜索到第12次时，第一次得到目标函数的最小值L，并一直稳定在“best_so_far”状态，即最优解时的设站代价值被认定为L=189 277.778 3。此外，从局部最优与全局最优的关系可以看出，搜索结果具有良好的收敛效果。

对比本文设计算法结果与3.1节穷举结果，有：

验证了算法的可靠性。

4 结 语

本文设计的基于随机因子构造邻域的禁忌搜索算法，能有效解决网络规划过程中的设站问题。实验分析显示，算法能够有效规避搜索陷入局部解，得到全局最优解。因此，可以通过少量的搜索次数，得到设站问题的最优解，减少求解此类问题的计算量。

[1] 周炯槃.通信网理论基础(修订版)[M].北京:人民邮电出版社,2009.ZHOU Jiong-pan.Communication Foundation Theoretical Basis(Revised)[M].Beijing:People's Posts and Telecommunications Press,2009.

[2] 任晓华,田宝玉.无线通信中站址规划优化的研究[EB/OL].(2013-03-21)[2017-11-21].http://www.doc88.com/p-8099994492323.html.REN Xiao-hua,TIAN Bao-yu.Research on Site Optimization Planning in Wireless Communication[EB/OL].(2013-03-21)[2017-11-21].http://www.doc88.com/p-8099994492323.html.

[3] 陈伟.WCDMA基站站址选择算法的研究[D].上海:上海交通大学,2006.CHEN Wei.Research on the Algorithm of WCDMA Base Station Site Selection[D].Shanghai:Shanghai Jiao Tong University,2006.

[4] 彭超.禁忌搜索求解排课问题的应用研究[D].西安:西安电子科技大学,2007.PENG Chao.The Application of Tabu Search in Solving the Problem of Scheduling[D].Xi'an:Xidian University,2007.

[5] 何汉武.数控等离子切割机的路径优化[D].上海:上海交通大学,2008.HE Han-wu.Path Optimization of Numerical Control Plasma Cutting Machine[D].Shanghai:Shanghai Jiao Tong University,2008.

[6] Glover F.Future Paths for Integer Programming and Links to Artificial Intelligence[J].Computers and Operations Research,1986,13(05):533-549.

[7] 贺一,刘光远,基于变异方法的禁忌搜索[J].计算机科学,2002,29(05):115-116.HE Yi,LIU Guang-yuan.Tabu Search Based on Mutation Method[J].Computer Science,2002,29(05):115-116.

[8] 袁庆达,闫昱,周再玲.Tabu Search算法在优化配送路线问题中的应用[J].计算机工程,2001(11):86-89.YUAN Qing-da,YAN Yu,ZHOU Zai-ling.Application of Tabu Search Algorithm in Optimizing Distribution Routing Problem[J].Computer Engineering,2001(11):86-89.

[9] 王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001.WANG Ling.Intelligent Optimization Algorithm and Its Application[M].Beijing:Tsinghua University Press,2001.

[10] A Multi-dimensional Tabu Search Algorithm for the Optimization of Process Planning[J].Science China(Technological Sciences),2011(12):3211-3219.

[11] Chen C H,Schonfeld P.Work Zone Optimization for Twolane Highway Maintenance Project[J].Transportation Research Record,2004(1877):95-105.