机器视觉中的尺度可控图像分割方法*

张 健

（长沙理工大学 物理与电子科学学院，湖南 长沙 410114）

0 引 言

随着计算机技术与数字图像技术的发展，拥有多种先进学科共同支撑的机器视觉，频繁活跃于视频监控、人脸识别、指纹识别及医用图像检测等[1]。如何提高图像处理系统的性能，一直是机器视觉的核心问题。作为图像处理系统中对图像进行预处理的关键一步，图像分割则成为辨别图像信息和研究图像特性的有效处理手段。通过对图像的分割操作，能够大幅降低图像处理的繁琐程度和不必要的冗长算法，使图像更容易理解和分析，从而为图像的后续操作提供便捷[2-3]。

图像分割方法多种多样。传统的图像分割是将像素点视作基本处理对象，而随着人们对图像认知的要求越来越高，尤其是对高清视频图像和3维图像，传统方法已然暴露缺点，即图像信息量大导致算法复杂、处理过程耗时耗力、处理结果与预期不符等。直到21世纪初期，出现了超像素这个新颖的概念[4]。后经学者们不断探讨研究，超像素在图像分割领域的地位愈发重要[5]。本文介绍机器视觉中的尺度可控图像分割方法，实际上就是以超像素为处理对象的新型超像素分割方法。

1 图像分割的数学定义

从数学观点出发，将图像分割按照集合的概念定义为：将整个待处理图像区域看成是非空全集U，则对该图像区域的分割便可以当成是将全集U划分成n个满足以下四个条件的非空子集U1,U2,…,Un，即图像的子区域。

分割后所有子区域的并集是原图像：

各子集Ri之间为连通区域，i=1,2,…,n；任两个子区域间有明显不同的特性：

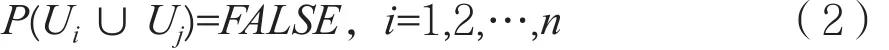
子区域内部有均匀一致的特性：

如上述定义，差异性、均匀性以及连通性成为最优图像分割方法的必备特性。详细来讲，差异性是指相邻子区域之间的图像特性差别应当显著；均匀性是指子区域内具有相似的颜色以及相似的灰度等；连通性是指分割成的子区域之间要紧凑、连接光滑、分割边沿无尖点。然而，实际操作中完全遵循上述三点实属不易，所以当今现有的分割算法只能将上述三点折中。

2 几何流理论

2.1 曲线演化理论

曲线演化理论是通过对曲线的单位法向量以及其曲率等几何特性的测度来研究曲线随时间演化的理论。一般地，演化曲线形变方向的数学特性为其单位法向量，曲线弯曲程度的数学度量方式是曲率。曲线演化理论在图像分割中的应用，实质上是把图像分割的过程近似看作图像定义域内闭合曲线在多种驱动下的演化过程。当曲线逼近到目标区域的轮廓时，则停止演化。

设二维图像定义域内的一条随时间变化的闭合曲线Q(l,t)=(x(l,t),y(l,t))，其中l表示曲线的弧长，t表示时间。Q的演化过程可由偏微分方程表示：

设曲线演化的一般速度为V(l,t)，表示图像上每个像素点的演化速度，则曲线的演化方程可以写为：

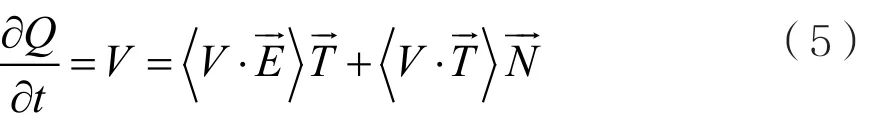
式中，依照切法线速度向将其上任意点速度分解，速度V(l,t)在切法两方向的分量用式（4）的A、B两参数表示，即V=(A,B)。

曲线演化时，参变量p随曲线沿切向的变化而变化，不可能影响演化曲线的几何形变，即V=(A,B)满足(A,B)=(0,B)。所以，可以去掉切向矢量，则曲线的演化方程（4）可简化为方程（6）：

图1给出了曲线演化模型。模型里曲线演化方向为法向，即曲线的扩展方向由黑色小箭头代表。

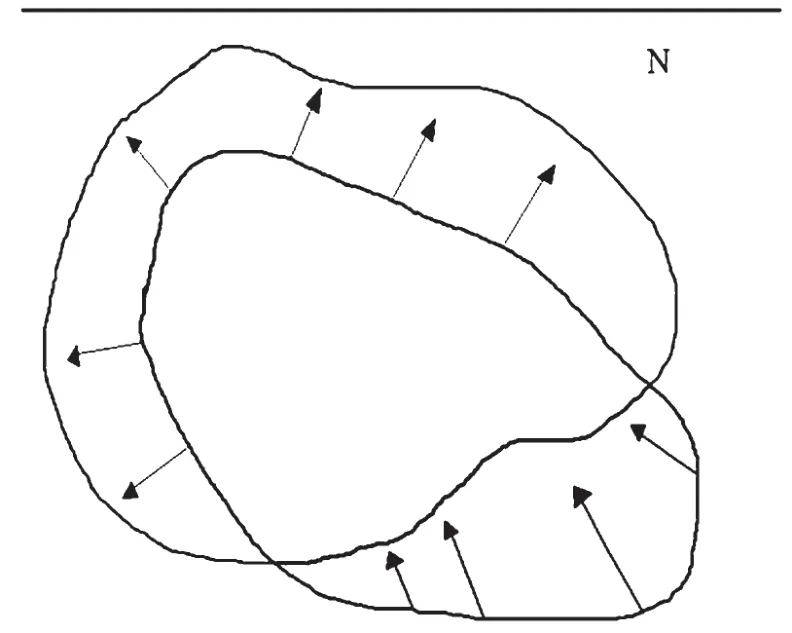
图1 曲线演化

曲线演化最常见的一种形式是曲率演化，其演化方程为：

曲线的另外形式——常值演化，可以用式（8）表述：

其中，V0代表曲线的演化速度及方向，是一个常值，可正可负可为零。

在常值演化方式中，演化曲线上任意点都依靠一个确定不变的速度扩展或是收缩，这样就会使曲线演化出不规则的尖点，进而导致曲线分裂，得出劣质的分割结果。曲率演化过程中，其上任意点的演化速度由曲率决定，即曲率越大，曲线运动速度越快；曲率越小，曲线演化速率越慢。这样便会出现平滑的曲线演化，无法形成棱角或者尖点，使其逐渐向圆形趋势运动。

2.2 水平集方法理论

水平集方法理论主要建立在数学思维的基础上，把低维表达嵌进高其一维n+1的函数f中，那么水平集函数就是此处的f。利用该思想可以快速处理曲线演化过程求解，将演化曲线Q(l,t)嵌进高其一维的水平集函数φ(x,y,t)中。

此处演化曲线用水平集函数的零水平集代表，即Q(l,t)={(x,y)|φ(x,y,t)=0}。一般地，这里可以用符号距离函数表示水平集函数，则水平集演化如式（9）为演化曲线的法向量。

详细来讲，如果需要判定当前时刻曲线Q(t)，那么从任一时间点t中拿出φ(x,y,t)=0的水平集。同时，即便曲线的拓扑结构改变，水平集函数φ始终保持有效性，式（9）也叫做Hamilton-Jacobi型偏微分方程。

在水平集方法的数值实现上，存在水平集的重新初始化问题。一般地，要将水平集函数初始化为符号距离函数。为了使水平集函数φ始终保持为一个有效的符号距离函数，引入“重新初始化”的方案，即每经过一段时间更正一次水平集函数φ，使其仍为一个有效的函数。该过程叫做水平集函数φ(x,y,t)的重新初始化。

3 尺度可控图像分割方法

3.1 算法的概述

首先将粒子排布于待分割图像上，粒子数可根据研究需要进行改变。然后，根据曲线演化理论，通过演化粒子边界曲线，最终将图像划分为一定数量能够保持一定图像局部结构特征的超像素子区域。一个超像素子区域对应一个可以演化的粒子。

粒子内部称作赋值区域，粒子之外的区域称作未赋值区域。处于赋值区域和非赋值区域间的粒子边界曲线逐步演化，直至稳定则停止演化。该算法最明显的优势在于能够保持粒子演化后生成的超像素子区域面积大致相同，生成速度快，相邻超像素子区域之间紧密且不重叠，同时还能人为设定所生成超像素子区域的数量，即实现尺度可控。另外，该算法抵抗图像噪声能力突出，主要是由于提取图像特征时往往在极小的超像素子区域中进行平均。图2为尺度可控图像分割方法的算法整体流程图。

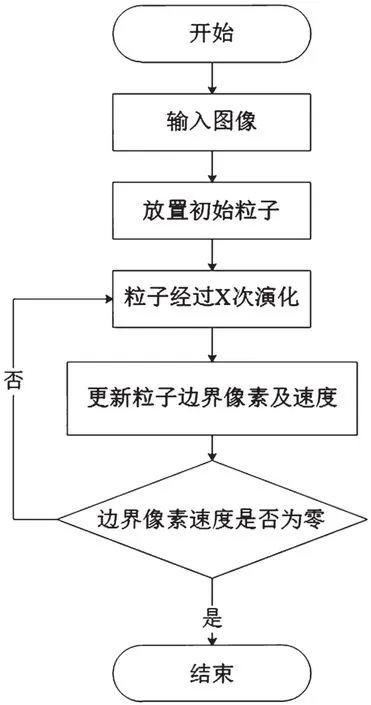
图2 算法整体流程

3.2 算法步骤

3.2.1 初始粒子的放置

设K代表超像素子区域的数量即粒子数，N代表待处理图像上的总像素点数，初始超像素块之间的距离约等于，初始粒子的大小等于一个像素点的大小。为了防止粒子演化后出现偶然被重叠的现象，此处还需根据待处理图像的灰度梯度，使初始粒子远离图像边缘。

3.2.2 粒子边界曲线的表示

粒子边界曲线的演化转化成曲面的演化，曲线作为该曲面的一个水平集存在于到其内部，待曲面完成演化，曲线演化结果便可从曲面的相应水平集获得。演化方程为：

Q是粒子边界曲线的坐标向量，t是粒子边界曲线的演化时间，N表示粒子边界曲线的外法线方向，S为演化速度。

设边界曲线为Q所对应连续平滑的曲面为H，那么每一个像素点的函数值在由H代表的一个图像平面上通过一个符号欧氏距离函数来确定，寻找距离该像素点最接近的粒子边界曲线Q。即若一个像素点在未赋值区域，则欧氏距离是正值；相反地，如果在已赋值区域，则欧氏距离是负值；而曲面H的零水平集就是超像素的边界。

3.2.3 粒子边界曲线的演化

此处，用低阶离散时间的方程表示曲面的演化，然后通过逐步迭代得到高阶的值：

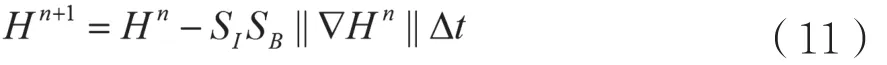
∆t表示粒子演化一次，SISB为粒子边界曲线的速度，是算法的核心。SB的值与粒子边界上的像素点和其他像素点的相似性有关，可称为“开关参数”，即置1时曲线开始演化，置0时曲线停止演化。而SI的值与粒子边界超像素的几何结构和局部像素结构有关，是核心中的核心。该参数的主要功能有两个：一是保证像素点速度在图像高灰度梯度区域降低；二是保证曲线向图像边缘演化。如果未达到图像边缘，那么曲线上的点在法向量上的运动方向与图像边缘的负梯度方向一致。紧接着，这些点被一个增大的牵引力驱动至图像边缘；相反地，如果曲线演化有着超过图像边缘的趋势，则被拉回。

3.2.4 粒子边界曲线演化停止

边界停止演化时，算法终止。因为理论上随着速度的快速降低，边界只能进行有限度的演化，所以当低于临界值的超像素覆盖的总图像区域相对增大时，运算法则停止。种子演化结束后的工作：首先将没有处理的连通局部作为超像素子区域；其次移除超像素子区域里面积较小的；再次将其设成未赋值区域；最后对未赋值的区域进行赋值，即继续演化，直到获得平滑的超像素边界。

整体算法的执行步骤如下：

输入：图像I，粒子数K

输出：超像素的边界B

将粒子K放在图像I的矩形网格中

让粒子远离高梯度区域

给粒子边界像素开始赋值

设Ψ0为已赋值区域内满足欧式距离的函数

计算像素的局部的灰度梯度φ(x,y)

n←0

当已赋值的像素点变化到最大时

计算图像的速度SI

计算边界的速度SB

S←SISB

在零水平集的一个窄频带Ψn的附近扩展速度S

在窄带通过迭代利用Ψn计算Ψn+1

n←n+1

已赋值的像素点←∑x,y[Ψn(x,y)＞=0]

B←Ψn同轮的骨架

返回B

3.3 算法特点

3.3.1 覆盖均匀

依据曲线演化理论，每一个粒子对应于一个像素点，这样做的目的在于放置初始种子的时候能够实现分布均匀。同时，超像素子区域拥有近似相同的尺寸，可实现最小目标区域与超像素尺度相等化。

3.3.2 超像素子区域不重叠

在粒子进行演化前，算法对曲线内外的像素进行差异性度量，然后根据度量结果设置一个启动值。只有差异性不大于这个启动值时，曲线才能开始演化，且每一次扩张前都要重新进行差异性度量并设置新的启动值，以避免粒子融合，提高分割的可靠性。

3.3.3 分割边沿平滑

由于该算法严格根据粒子边缘曲线的曲率和粒子周围像素点的灰度梯度实现对演化速度的控制，使得生成的超像素子区域边界光滑无尖点，同时又保留了原有图像的细节信息。

4 实验结果

本文实验利用Matlab R2016a软件对机器视觉中的尺度可控图像分割方法的图像处理效果进行验证。程序的输入为可以演化的粒子，输出为超像素边界，实验结果如图3所示。

图3 尺度可控图像分割实验

图3（a）展示了粒子演化的过程，其中第一幅图为粒子的初始位置，此处粒子数为1 000，第二幅图为粒子演化10次的结果，第三幅图为粒子最终停止演化的结果，即最终分割。

图3（b）展示了利用所提方法对图像进行分割处理的整体与细节效果，图中的鹰为目标区域，也称作感兴趣区域，粒子数同样设置为1 000，程序运行大约5 s后出结果。可见，分割后目标区域的轮廓信息被保留。

5 结 语

本文提出的机器视觉中的尺度可控图像分割方法对图像细节信息处理能力突出，分割所需时间短，且可根据研究需要人为控制分割密度。该算法将数据驱动型曲线演化过程的趋势与一组基于图像骨架的外部约束相结合，形成了一种新颖、高效的图像分割方法，可用于超高清视频图像的研究。

[1] 于翔.机器视觉中几种颜色优势的图像分割算法比较与研究[J].无线互联科技,2012(09):20-28.YU Xiang.Comparison and Research on Image Segmentation Algorithms of Several Color Advantages in Machine Vision[J].Journal of Wireless Internet Technology,2012(09):20-28.

[2] 姜枫,顾庆.基于内容的图像分割方法综述[J].软件学报,2017,28(01):160-183.JIANG Feng,GU Qing.Survey on Content-Based Image SegmentationMethods[J].Journal of Software,2017,28(01):160-183.

[3] 彭红星,邹湘军.基于演化算法的水果图像分割[J].农业工程学报,2014,30(18):294-301.PENG Hong-xing,ZOU Xiang-jun.Fruit Image Segmentation Based on Evolutionary Algorithm[J].Transactions of the Chinese Society of Agricultural Engi neering,2014,30(18):294-301.

[4] 宋熙煜,周利莉,李中国.图像分割中的超像素方法研究综述[J].中国图象图形学报,2015,20(05):599-608.SONG Xi-yu,ZHOU Li-li,LI Zhong-guo.A Review of Superpixel Method in Image Segmentation[J].Journal of Image and Graphics,2015,20(05):599-608.

[5] 许新征,丁世飞,史忠植等.图像分割的新理论和新方法[J].电子学报,2010,38(S1):76-82.XU Xin-zheng,DING Shi-fei,SHI Zhong-zhi,et al.New Theory and Method of Image Segmentation.[J].Acta Electronica Sinica,2010,38(S1):76-82.