一种确定性测量矩阵与快速恢复算法*

唐川雁，朱 皓

（杭州电子科技大学 通信工程学院，浙江 杭州 310018）

0 引 言

压缩感知（Compressed Sensing，CS）因采样率不受奈奎斯特采样定理的限制且可以基本无失真地恢复出原始信号，成为无线通信、生物传感等领域的热门研究方向。

压缩感知的关键是测量矩阵的构造和恢复算法的设计。具体地，测量矩阵与稀疏基之间的相关性尽量要小，在对信号进行观测实现降维处理时，不破坏信号中的有用信息；恢复算法应采用尽量少的测量值快速准确地恢复信号。Candes等人提出约束等距性质（Restricted isometry property，RIP）[1]来判断测量矩阵的性能优劣。常用的随机测量矩阵均满足此性质，如高斯随机矩阵、傅里叶随机矩阵等。但是，它的硬件实现和对应恢复算法的设计较复杂，实用性差。因此，Haupt和Bajwa等人提出了托普利兹矩阵、循环矩阵[2-5]，Bajwa等人提出了结构化随机矩阵[6]，均为确定性测量矩阵，但这些矩阵相比高斯随机矩阵重构效果较差。Ronald A DeVore提出利用多项式方法来构造确定性测量矩阵[7]，但其对图像的压缩倍数有限。文献[8]提出二元置换块对角测量矩阵（Binary Permuted Block Diagonal，BPBD）。高度稀疏结构传感效率高，与常用的稀疏基如小波基等不相关，组成元素简单、易于硬件实现且重构效果较理想，但其置换过程繁琐。

本文提出一种简单的二元块对角（Binary Block Diagonal，BBD）确定性测量矩阵，能够降低测量矩阵的计算复杂度，有效促进硬件实现，节约成本。恢复算法分为贪婪算法和凸松弛算法。贪婪算法应用广泛，典型的有出现时间较早的匹配追踪（Matching Pursuit，MP）算法[9]。后续许多算法都是在MP算法基础上改进而来的，如正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法[10]、分段式正交匹配追踪（Stagewise Orthogonal Matching Pursuit，StOMP）算法[11]等。OMP算法逐步向前迭代，在余量更新时引入Schmidt正交化处理，不会出现原子的重复选择，加快了算法的收敛过程，但因其每次迭代过程中的正交化处理使得运算量加大。StOMP算法在OMP算法基础上每次迭代选择多列，加速了恢复过程，但其对已选原子不能进行再次筛选，加大了原子误选概率。本文提出基于离散余弦变换域（Discrete Cosine Transform，DCT）[12]的快速恢复算法。在DCT域中，利用阈值来控制信号的稀疏水平，可预知所提测量矩阵的有效列位置，不需要在每次迭代中寻找与当前残差的最匹配原子，从而可以高效恢复原始信号。

1 压缩感知基本理论

设在RN空间中存在一个长度为N的离散信号X，可看作是一个N×1维的列向量。现假设有一组基函数Ψi(i=1,2,…,N)也是N×1维的，若X可用Ψi的线性组合来表示，令Ψi=[Ψ1,Ψ2…,ΨN]，则X可表示为：

式 中 Ψ 为 稀 疏 基（ 变 换 基），α=[α1,α2…,αN]T称为稀疏矢量。若矢量α只存在至多K个非零值或重要元素，可认为该信号在变换基上是稀疏的，稀疏度为K。CS通过矩阵Φ∈RM×N对信号X(X∈RN)进行观测实现降维处理，其中K＜M＜N，得到的矢量y∈RM叫做测量矢量（测量值），表达式为：

式中A=Φ×Ψ∈RM×N为恢复矩阵，Φ为测量矩阵。

从测量值y中重构出原始信号X的过程叫做CS的恢复过程，即求解式（2）。因为A不是一个方阵(M＜N)，所以式（2）是一个NP-hard问题。但是，由于X对于基Ψ有稀疏表现，所以恢复过程可由下列步骤完成：

①求稀疏矢量α～：

②重构信号：

如果存在一个约束等距常数δK,0＜δK＜1，使得恢复矩阵A与稀疏矢量满足：

则可认为测量矩阵满足RIP条件。只有当测量矩阵满足该条件时，重建原始信号才能实现。它的等价条件是测量矩阵Φ与稀疏基Ψ不相关。这个条件相比于RIP条件，在实际中更容易证明。通常，用相关系数μ表示这两个矩阵之间的相关性：

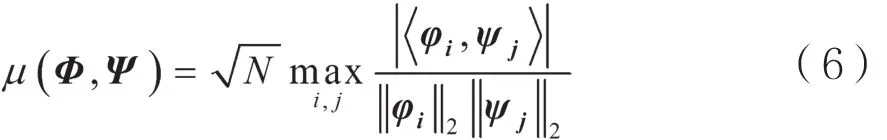
式中φi, i∈{1,2,…,M}代表Φ的行矢量，Ψj,j∈{1,2,…,M}代表Ψ的列矢量。

2 DCT域的阈值处理

稀疏度K的值越小，恢复原始信号所用的测量值越少。因而，应当遵循使得K值尽可能接近0这一原则选择稀疏基Ψ。常用的稀疏基有小波基、Gabor基和DCT基，也可以通过字典学习训练法生成稀疏基。此外，为了控制稀疏度K的值，还可以采用阈值法。

DCT已广泛用于图像与视频的压缩[13]，也可用于压缩心电图和肌电图等生理信号。DCT的变换矩阵为：

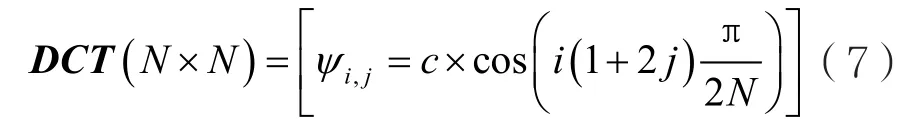
式中 i∈ {0,1,…,N-1}和 j∈ {0,1,…,N-1}分别代表矩阵的行和列的数值，而c是一个常数，定义为：

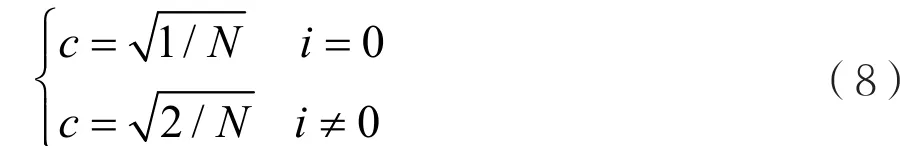
DCT矩阵是正交的，所以它的逆矩阵可通过转置获得，即IDCT=DCTT。DCT可将信号的大部分有用信息集中在低频分量上，而高频分量上的值通常较小，可以舍弃。因此，可以在DCT域采用类似的阈值法控制稀疏度K的大小，仅保留低于设定阈值的低频分量，从而降低恢复过程的复杂度。

3 二元块对角确定性测量矩阵

测量矩阵最初使用的是高斯或贝努利等随机测量矩阵，它们的元素均独立服从高斯分布或贝努利分布。这类矩阵满足RIP性质且能与多数变换基不相关，有较好的重构性能，但计算复杂度高、占用存储空间大，因此在硬件实现上比较困难。为了降低硬件实现的成本，本文提出了一个简单的二元块对角确定性测量矩阵，其构造方式为：

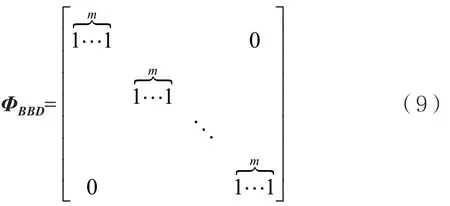
每一行有一个非零块，每个块中都包含m=N/M个元素且均为1，每个块的位置如式（9）所示，其余元素均为0，其中M和N分别表示矩阵的行和列。

矩阵ΦBPBD可以通过对ΦBBD的列进行置换来生成。由于舍弃了置换过程，所以文中提出的测量矩阵ΦBBD在结构上更加简单，硬件上也更容易实现。

4 基于阈值法的快速重构算法

本文在DCT域中完成阈值法。正如前文所述，DCT将大部分信号信息集中在低频分量上，剩余的高频分量在没有明显损失的情况下可以舍弃，阈值法即在预先定义的阈值下保持仅有的频率分量。阈值法在式（3）的过程中完成，能够促进CS的恢复。本文提出基于DCT阈值法的简单、快速的恢复算法。

根据提出的确定性测量矩阵ΦBBD，结合恢复矩阵的定义，可以得到：

由式（10）可知，恢复矩阵A与ΨIDCT结构几乎相同，它的列向量 [∂1,∂2,…,∂N]分别对应于从低频到高频的分量。由于提出的ΦBBD是一个确定性矩阵，而ΨIDCT是已知的，因此可事先得知恢复矩阵A中有效列的位置，极大地提升信号的重建效率。

下面给出本文所提恢复算法的实现过程：

输入：测量向量y，测量矩阵ΦBBD

①初始化：A=ΦBBD×ΨIDCT；

②选择 A 中前 M 个原子：AM=[∂1|∂2|…∂N]；

③求解线性方程组y=AMα^M；

④得到稀疏矢量 α^=[α^M|0…0]；

⑤输出信号稀疏估计 X^=ΨIDCTα^。

步骤②直接将恢复矩阵A的前AM个原子取出构成AM，实际等效于在DCT域中进行阈值处理，仅保留用来恢复信号的M个低频分量。经过这一处理，便可用于信号的重建，这样在步骤③中仅需求解一个线性方程组，大大简化了信号的恢复过程。另外，由于不需要在每次迭代中寻找与当前残差最匹配的原子，故该算法恢复效率较高。

5 仿真结果与分析

对本文所提的BBD确定性测量矩阵进行仿真，从与IDCT矩阵之间的相关性和对信号的重建概率两方面性能进行实验。为了比较，对高斯测量矩阵和BPBD测量矩阵也进行了仿真实验。选择OMP算法、StOMP算法与本文所提基于阈值法的快速恢复算法进行仿真，比较了三种算法对信号的重建概率和它们的恢复时间。

5.1 对所提BBD测量矩阵的性能分析

将所提测量矩阵ΦBBD、ΦBPBD和ΦGaussian作对比分析，分别计算三种不同测量矩阵与IDCT矩阵间的相关性与不同M值之间的关系，其中相关性用式（6）的相关系数来描述。实验中，原始信号长度N取500，测量值M以50为步进遍历50～450，得到三种测量矩阵与IDCT的相关系数随M的变化曲线，如图1所示。由图1可知，高斯测量矩阵与IDCT矩阵的相关系数μ最大，且μ的值随着M的增大没有持续减小。而BPBD矩阵和BBD矩阵的相关系数随着M的增大而减小，当M≥100时，BBD矩阵与BPBD矩阵的相关系数接近。可见，本文提出的BBD测量矩阵与BPBD测量矩阵在相关性方面性能一致，且明显高于高斯测量矩阵。

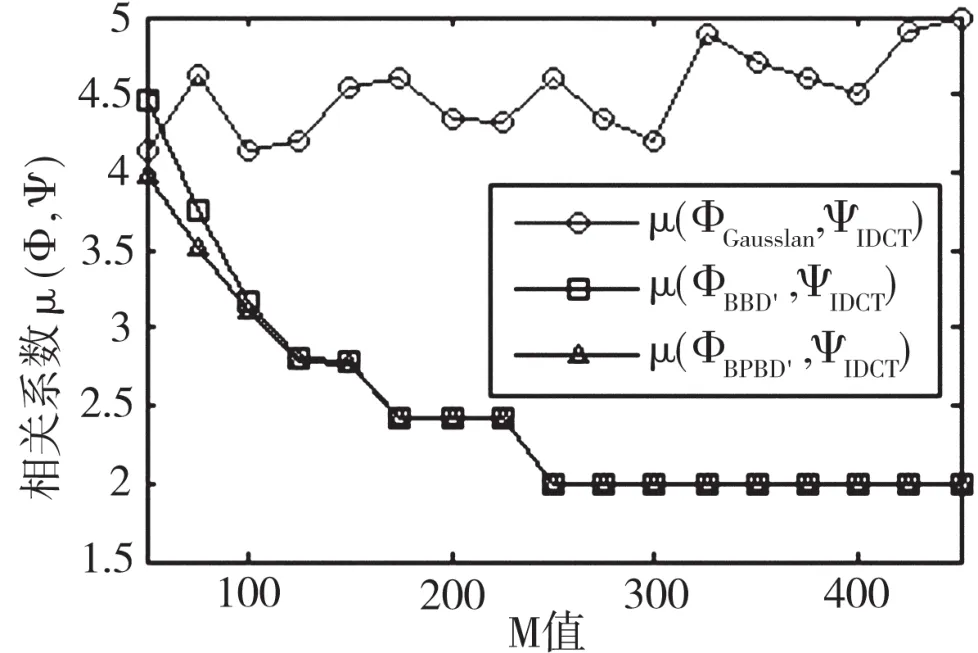
图1 三种矩阵的相关系数比较结果

下面比较三种测量矩阵对信号的重建概率，恢复算法采用OMP算法，原信号长度N取500，分别取M为35、45，用三种测量矩阵对原始信号进行观测，稀疏度K以1为步进遍历1～50，重复实验100次求平均重建概率，得到如图2所示的重建概率随稀疏度的变化曲线。

图2 三种测量矩阵对信号的重建概率

由图2可知，使用OMP恢复算法时，本文所提的BBD矩阵在K＜M时重建概率高于高斯随机矩阵、BPBD矩阵，且只有当K接近M时重建概率才开始下降，而高斯随机矩阵和BPBD矩阵在K远小于M时就开始下降，说明用所提的BBD矩阵，OMP算法的性能明显提高。

5.2 对所提基于DCT阈值法的恢复算法性能分析

用所提的BBD测量矩阵对信号进行观测，分别用基于DCT阈值法的恢复算法和OMP算法、StOMP算法对信号进行恢复，对信号的压缩程度用压缩比进行描述，压缩比定义如下：

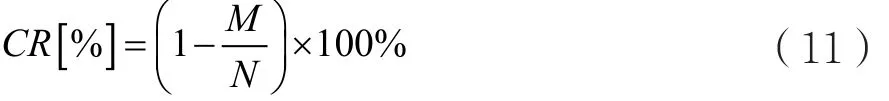
式中M为测量向量的长度，N为原始信号的长度。

用本文所提的BBD测量矩阵分别取M为35和45对原始信号进行观测，然后分别用三种恢复算法对测量值进行恢复，做出重建概率随稀疏度的曲线如图3所示，同样的重建概率为重复实验100次的平均重建概率。

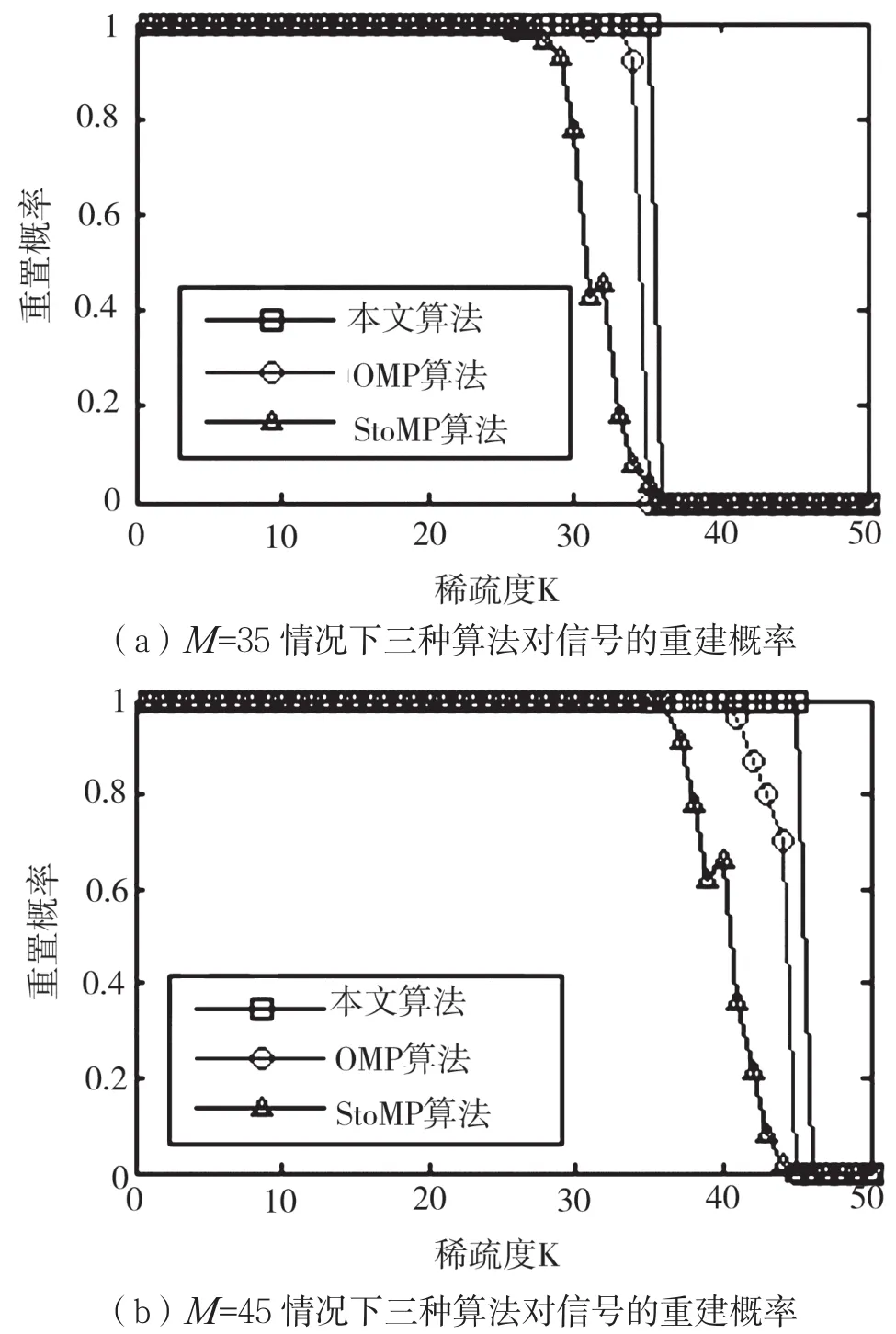
由图3可知，在M为35时，OMP算法和StOMP算法需要稀疏度分别小于33和26时重建概率为100%，而所提恢复算法在稀疏度小于等于M时重建概率均为100%；M为45时，OMP算法和StOMP算法需要稀疏度分别小于41和35时重建概率为100%，而所提恢复算法在稀疏度小于等于M时重建概率均为100%。这说明在不同测量值M时，本文所提的恢复算法均可以在小于等于M的稀疏度下准确重构原始信号，而OMP算法、StOMP算法需要稀疏度较小时才能准确重构原始信号。所以，在重构概率上，本文所提出的基于DCT阈值法的恢复算法是性能最好的。

下面比较所提快速恢复算法、OMP算法、StOMP三种算法的恢复时间Tr和平均信噪比在不同压缩比CR下的情况，结果如图4所示。

图4 信噪比和恢复时间与压缩比的关系曲线

由图4可知，随着压缩比的增大，三种算法的恢复时间都减小，说明测量点数越少，恢复信号所用时间越短。由于OMP算法需要多次迭代选择与残差最匹配的原子，所以其恢复时间最长，而StOMP算法在每次迭代过程中选择了多个原子，所以在相同压缩比下比OMP算法恢复时间短。而所提基于DCT阈值法的快速重构算法完全舍弃了迭代选择最佳原子的过程，因此在相同压缩比下重构效率最高，所用的恢复时间最短，比OMP算法、StOMP算法的速度均快了10倍以上。由平均信噪比与压缩比CR之间的关系曲线可看出，在相同压缩比下，所提恢复算法的信噪比比OMP算法、StOMP算法大，说明提出的基于DCT阈值法的快速恢复算法相比于OMP算法、StOMP算法具有更好的性能。

6 结 语

针对传统随机测量矩阵的不足，提出了一种简单的确定性测量矩阵，即二元块对角确定性测量矩阵，并基于此测量矩阵对信号进行观测降维，提出了在DCT域完成阈值处理且简单快速的恢复算法。仿真实验的结果表明，所提测量矩阵与随机测量矩阵相比，在重构概率上具有更好的性能，且所提恢复算法在同等压缩比下的信噪比均高于OMP算法、StOMP算法，所需的恢复时间也比OMP算法、StOMP算法快了10倍以上。

[1] Candès E J.The Restricted Isometry Property and Its Implications for Compressed Sensing[J].Comptes Rendus Mathematique,2008,346(09-10):589-592.

[2] Rauhut H.Circulant and Toeplitz Matrices in Compressed Sensing[m].Mathematics,2009.

[3] Bajwa W U,Haupt J D,Raz G M,et al.Toeplitz-Structured Compressed Sensing Matrices[C].Statistical Signal Processing,2007:294-298.

[4] Yin W.Practical Compressive Sensing with Toeplitz and Circulant Matrices[C].Proceedings of SPIE-The International Society for Optical Engineering,2010:7744.[5] Sebert,Florian Z,Yi M,et al.Toeplitz BlockMatrices in Compressed Sensing and Their Applications in Imaging[C].Information Technology and Applications in Biomedicine,2008:47-50.

[6] Do T T,Tran T D,Gan L.Fast Compressive Sampling with Structurally Random Matrices[C].IEEE International Conference on Acoustics,Speech and Signal Processing IEEE,2008:3369-3372.

[7] Devore R A.Deterministic Constructions of Compressed Sensing Matrices[J].Journal of Complexity,2007,23(04):918-925.

[8] He Z,Ogawa T,Haseyama M.The SimplestMeasurement Matrix for Compressed Sensing of Natural Images[C].IEEE International Conference on Image Processing,2010:4301-4304.

[9] Mallat S G,Zhang Z.Matching Pursuits with Timefrequency Dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.

[10] Tropp J,Gilbert A C.Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[11] Donoho D L,Tsaig Y,Drori I,et al.Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2012,58(02):1094-1121.

[12] Khayam S A.The Discrete Cosine Transform(DCT)[M].London:Digital Image Processing. Springer,2008:367-373.

[13] Li Q,Han Y,Dang J.Image Decomposing for Inpainting Using Compressed Sensing in DCT Domain[M].New York:Springer-Verlag Inc.,2014.