带螺线盘线圈的Ku波段径向渡越时间振荡器模拟研究

陈永东

(四川理工学院物理与电子工程学院， 四川自贡643000)

引言

在过去的20多年里，高功率微波(HPM)系统在峰值功率、脉冲能量以及重复频率等多个指标上取得了长足的进步，但HPM系统距离实际应用还面临着诸多技术挑战。在很多应用场景中，HPM系统被要求安装在狭小的、有限功率供给的移动平台上，这对HPM系统的体积、重量、效率等指标提出了非常严苛的要求。发展紧凑、轻便、高效的HPM系统成为当前HPM研究中的热点问题之一[1]。为实现HPM系统的小型化和轻量化，通常要求HPM源工作在较低的二极管电压，引导磁场尽可能低[2]，同时具有较高的束波转换效率等。

相比于轴向渡越时间振荡器(transit-time oscillator, TTO)[3-6]，径向TTO的电子束的电流密度更低，空间电荷效应更弱，因此其束波转换效率可能更高，同时所需要的引导磁场也更低。另外，维持径向电子束传输的工作电压更低。这几方面都有利于HPM系统的小型化和轻量化。因此，采用径向电子束的HPM源在最近的十余年得到了广泛的关注和深入的研究,径向TTO作为传统的轴向TTO的变种，是目前最有潜力的径向HPM器件之一[7-12]。与轴向TTO类似，径向TTO通常采用高熔点的金属栅网[7-14]，如钨等引导强流电子束。在某些场合，金属栅网还扮演微波谐振腔的作用，实现电子束的调制和微波能量的提取。采用金属栅网的TTO最大的优点是不需要额外的磁场引导径向电子束传输，但是带栅网的TTO也有很多难以克服的缺点。首先，栅网会拦截或散射部分电子，这将影响电子束的数量及品质，导致器件的效率低下；此外，金属栅网在强流电子束的轰击下很容易加热并熔化，这限制了器件的重复频率和工作寿命，同时轰击产生的等离子体还会引起微波脉冲缩短等问题[12-13]。为克服带栅网TTO的上述缺点，设计了一种无栅网的Ku波段径向TTO，利用螺线盘线圈产生所需要的径向磁场对径向发射电子束进行引导，取代金属栅网的作用。粒子模拟显示，器件在电子束电压300 kV、电流15 kA条件下，可以产生功率2.07 GW、频率14.86 GHz 的高功率微波，束波转换效率达34.5%。

1 径向磁场产生

在大部分螺线管线圈的设计中，更关心的是线圈的Bz分布，而对Br分布不甚关心[15]。为产生满足径向电子束稳定传输的径向磁场分布，重新推导了线圈的磁场分布。圆柱坐标系下，电流元产生的磁场分布可以表示为：

(1)

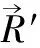
(2)

式中，I0是线圈电流，a为线圈半径，z′为线圈的轴向位置。

根据式(2)，可以给出不同半径的单匝线圈产生的径向磁场分布，由图1中“单线圈”曲线分别给出了半径a=5 cm、7 cm、9 cm、11 cm的线圈产生的径向磁场沿径向的分布。可以看出，Br分布与高斯分布类似，并且Br的最大点对应的半径与线圈半径一致。同时，单匝线圈产生的Br沿径向无均匀区，因此仅靠单匝线圈的磁场是无法引导电子束的稳定传输。进一步地，研究了沿径向圈绕的多匝螺线盘线圈产生的径向磁场：

(3)

式中，n为单位半径的匝数，r1和r2分布是螺线盘的最小和最大半径。由图1中“螺线盘”曲线给出了线圈电流950 A、50匝、内径4.4 cm、外径11 cm的螺线盘产生的径向磁场分布。可以看到，在半径5.5 cm到9.7 cm的区域，Br均超过了0.3 T 。

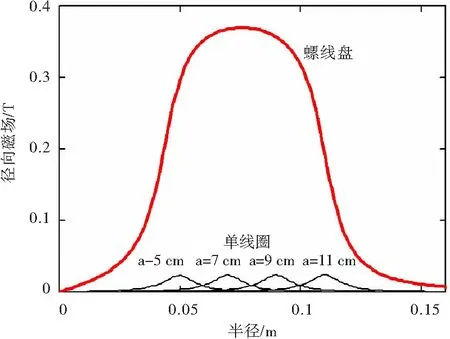
图1 不同线圈配置下径向磁场沿半径方向的分布

图2为单螺线盘和双螺线盘产生的径向磁场分布对比，两单螺线盘分别位于z′=0和z′=22 mm，选取的参考面位于两个螺线盘的中点即z=11 mm。可以看到，当参考面选择在两个螺线盘中点时，两个单螺线盘各自的Br分布完全相同，而双螺线盘的径向磁场是单螺线盘的两倍。图3是单、双螺线盘线圈产生的径向磁场沿轴向的分布。可以看到，单螺线盘的Br分布沿z向是逐渐减小的，而采用双螺线盘线圈的Br分布在两螺线盘之间是近似均匀的。因此为保证电子束的稳定传输，可以采用双螺线盘线圈在电子束通道内产生沿轴向和径向近似均匀的Br分布。

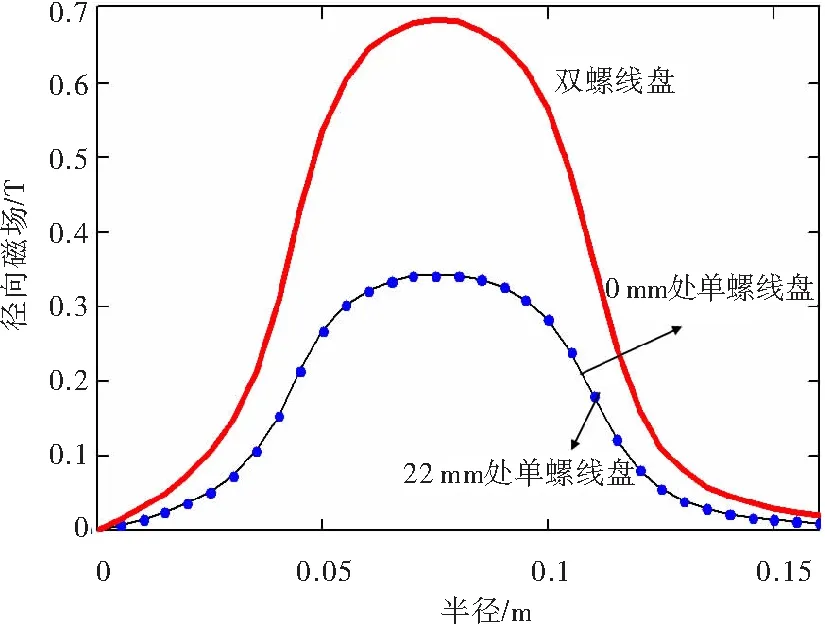
图2 不同线圈配置下径向磁场沿径向的分布

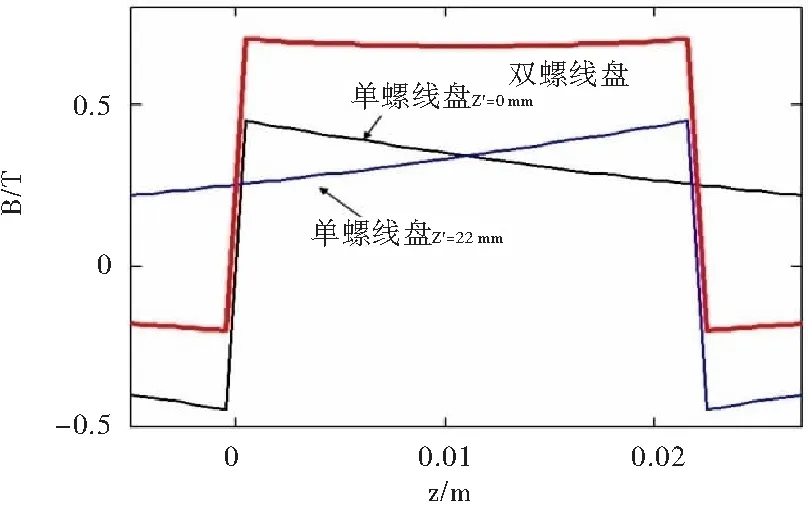
图3 螺线盘线圈径向磁场沿轴向的分布

根据上面的计算结果，可以绕制双螺线盘线圈的模型如图4所示。图5是根据上述参数在PIC软件中建立的双螺线盘线圈模型产生的径向磁场分布。由图5可知，径向磁场在电子束通道内的分布均匀，均匀区磁场强度0.68 T，后续章节中将开展基于该磁场分布的Ku波段TTO的整管粒子模拟。

图4 双螺线盘线圈模型

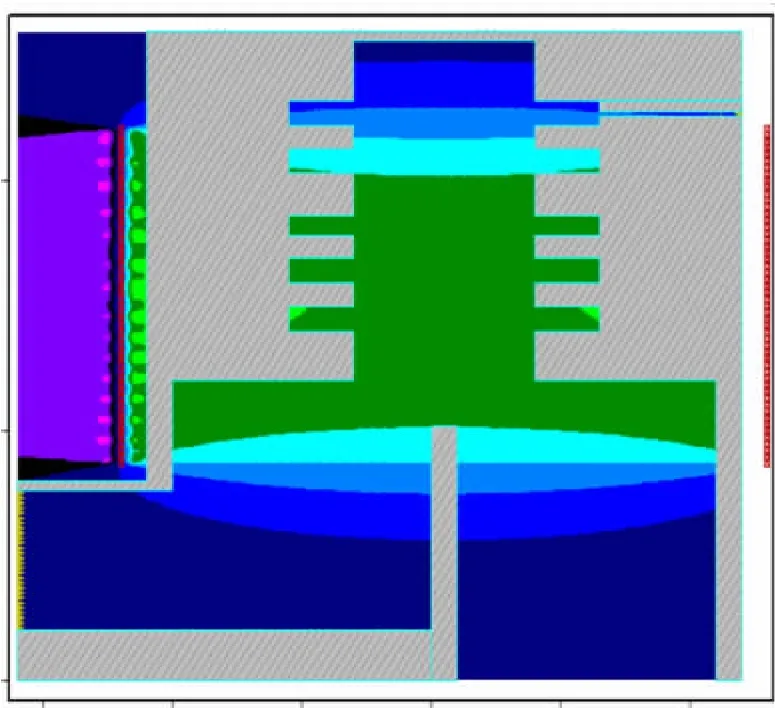
图5 双螺线盘线圈产生的径向磁场分布

2 径向电子束的空间电荷势能

如果忽略电子束沿z向的厚度，同时假定电子束的初始半径为rb，初始入射相对论因子为γinj，径向传输线的宽度为L，则电子束的空间电荷势能可以表示为[9]：

(4)

式中，vb是电子束在径向传输线内的运动速度，I0为电子束电流。由能量守恒，有：

(5)

(6)

电子束达到空间电荷限制流状态的势能表示为：

(7)

由此，可以给出空间电荷限制电流Iscl：

(8)

联立式(4)和式(5)，可以给出电子束在径向传输线内空间电荷势能和空间电荷限制电流。图6是电压300 kV、电流20 kA的电子束在宽0.7 cm的径向传输线内的势能以及空间电荷限制电流沿半径的变化曲线。由图6可知，随着半径的增大，电子束电流密度逐渐减小，由此导致空间电荷势能逐渐减小，可提取的电子束动能逐渐增加，这也是径向TTO拥有较高束波转换效率的原因。图7为径向传输线内直流电子束的电子动能相空间分布，其也印证了理论分析。由图7可知，电子束在通过二极管的加速间隙进入到器件内部以后，随着半径的增加，动能逐渐增大。图6空间电荷限制流曲线可以看出，当阴极半径选择为5.1 cm, 相应的空间电荷限制流为30 kA，高于模拟采用的20 kA，不会在二极管区形成虚阴极。

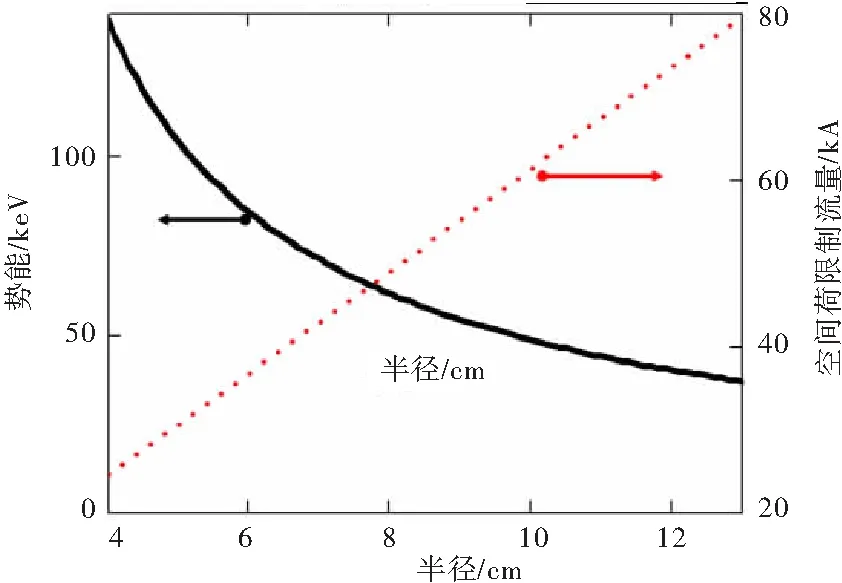
图6 势能和空间电荷限制电流沿半径的变化曲线

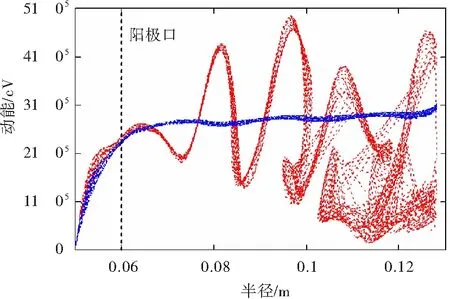
图7 直流和调制电子束电子动能的相空间分布

3 粒子模拟结果

径向传输电子束的引导磁场由双螺线盘线圈提供。双螺线盘线圈的均匀区径向磁场强度达0.68 T，阴极表面的磁场强度为0.54 T。由图8径向TTO内电子束分布可知，阴极爆炸发射的强流电子束能很好地被双螺线盘线圈产生的磁场约束，无电子轰击管壁。

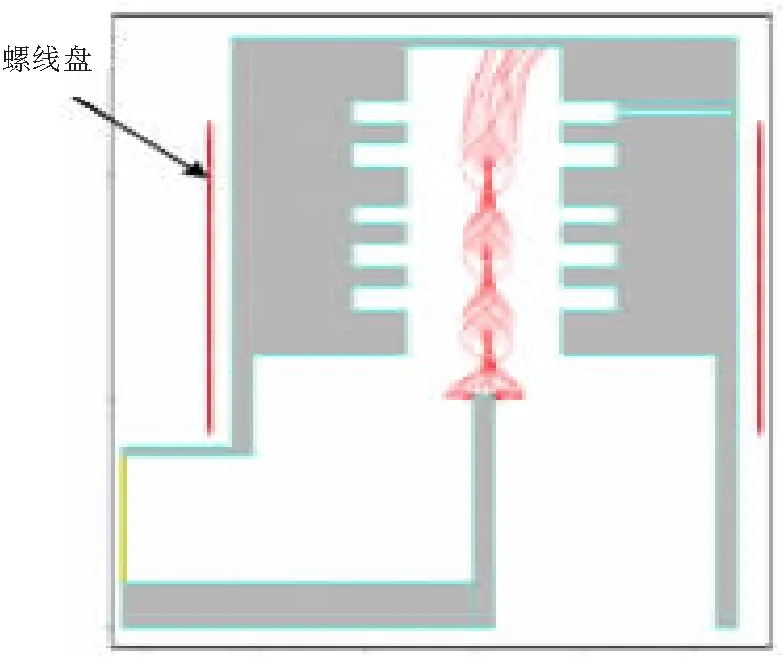
图8 Ku波段径向TTO模拟模型和电子束分布

图9是输出微波功率的射频以及包络波形，图10是输出微波电场频谱。在电子束电压300 kV、电流15 kA条件下，器件输出功率2.07 GW，效率34.5%，频率14.86 GHz。

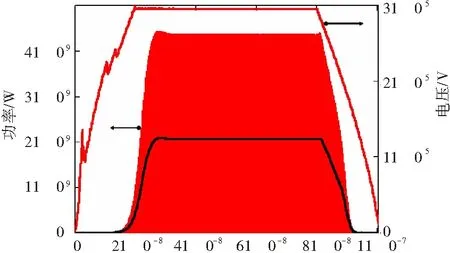
图9 电子束电压、输出微波功率的射频及包络波形

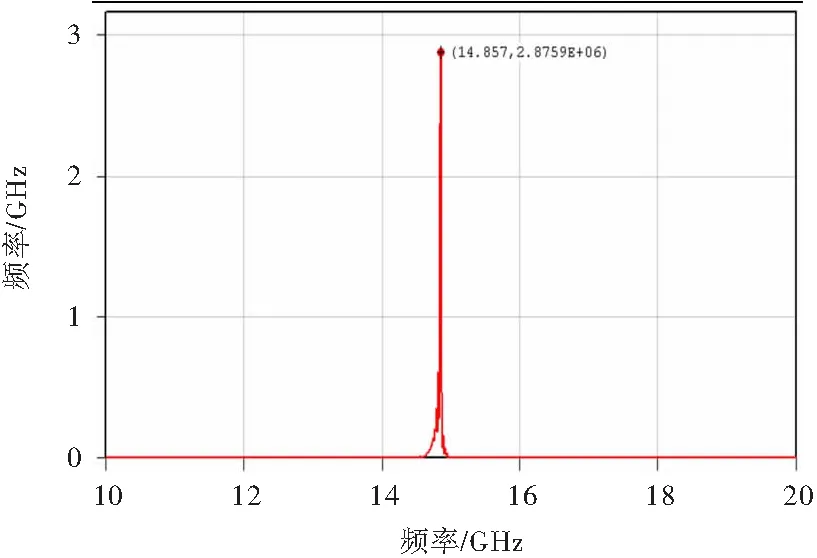
图9输出微波电场频谱

4 结束语

本文设计并研究了一种无栅网的Ku波段径向TTO，相比于传统的有栅网TTO，重复频率和工作寿命有了显著提高。详细研究了径向磁场的产生，并开展了带螺线盘线圈的Ku波段径向TTO整管粒子模拟。模拟结果显示，器件在电子束电压300 kV、电流15 kA条件下，可以产生功率2.07 GW、频率14.86 GHz 的高功率微波，束波转换效率达34.5%。

[1] BENFORD J,SWEGLE J A,SCHAMILOGLU E.High power microwaves[M].2ndEdition.NewYork:Taylor& Francis,2006.

[2] LING JP,ZHANG JD,HE JT,etal.A novel Ku-band transit radiation oscillator with external guiding magnetic field[J].Physicsof Plasmas,2014,21(2):1075-1082.

[3] 令钧溥. Ku 波段低磁场同轴渡越时间振荡器的研究[D].长沙:国防科技大学,2014.

[4] 练琳. Ku波段渡越时间振荡器的锁相研究[D].长沙:国防科技大学,2014.

[5] 何琥.X波段六腔轴渡越时间振荡器的理论和实验研究[D].绵阳:中国工程物理研究院,2003.

[6] 令钧溥,张建德,贺军涛,等.改进型低阻类膜片同轴渡越时间振荡器[J].强激光与粒子束,2013,25(11):2943-2947.

[7] 吴中发,王玉芝.径向速调管振荡器的理论设计与数值模拟[J].强激光与粒子束,2000,12(2):211-214.

[8] 贾云峰,刘永贵,李传胪.径向渡越时间振荡器的数值模拟[J].强激光与离子束,2002,14(1):95-98.

[9] 李少甫,杨中海.新型高功率径向三腔渡越时间振荡器数值模拟[J].强激光与粒子束,2008,20(2):473-478.

[10] 臧杰锋,刘庆想,朱静.径向三腔渡越时间振荡器数值模拟[J].强激光与粒子束,2008,20(3):473-476.

[11] ATMAN M J.Radial acceletron,a new low-impedance HPM source[J].IEEE Transactions on Plasma Science,1996,24(10):964-969.

[12] DANG F C,ZHANG X P,QI Z M,et al.Simulation investigation of a Ku-band Radial line oscillator operationg at low guiding magnetic field[J].Physics of Plasma,2014,21(6) :70-81.

[13] KONG L,LIU Q X,Li X Q,etal.Coaxialfoilless diode[J].AIP Advances,2014,4(5):4626-4664.

[14] CAO YB,HE JT,ZHANG JD,etal.High power microwave generation from the low-impedance transit-time oscillatiorwithout foils[J].Physicsof Plasmas,2012,19(7):0721061-0721064.

[15] 王华军,李宏福,温越琼.螺线管中磁场的计算[J].四川轻化工学院学报,1999,12(4):23-25.