暗挖地铁区间施工对周边环境的影响研究

陈 菊

随着中国经济的快速发展，现有城镇的地上空间已经不能满足人民日益增长的需求，所以大力开发地下空间逐渐成为主要趋势，其中隧道工程是应用最为广泛的手段［1－3］。在城市隧道施工过程中，隧道开挖会对原有地层产生扰动并使地层应力改变，从而造成地表较大变形及路面塌陷等情况，严重威胁到人民的生命财产安全，所以需要对隧道开挖时的地表沉降及隧道本身的变形情况进行深入研究与有效控制［4－5］。

对于隧道变形与地表沉降的分析，有很多较为成熟的方法，包括理论计算、模型试验及数值模拟等［4－8］。其中伴随着计算机科技的发展，由于数值模拟更能直观地展现出隧道开挖时的土体变形等相关分析结果，避免较大工程问题的出现而逐渐成为最普遍也是应用最广泛的分析方法。

刘波等［9］应用大型有限差分软件 FLAC2D／3D对盾构施工期间地表沉降对某购物中心建筑基础的影响程度进行分析并给出合理的解决方案。赵华松［10］通过三维有限元数值模拟的方法对上海地铁明珠线某处的隧道区间施工出现的地表沉降情况进行分析，并结合模拟结果与实际的监测数据综合分析得到隧道开挖时影响范围内的地层沉降规律，并利用计算机技术开发出了隧道施工力学分析系统。杨福麟等［11］利用大型通用岩土工程分析软件MIDAS／GTS对武汉地铁虎名区间采用矿山法进行的隧道开挖工程为背景，对施工过程的隧道变形及地表沉降情况进行分析，提出了隧道开挖期间的围岩优化方案。曹波等［12］通过地铁暗挖隧道施工的数值分析，并结合现场监测结果进行对比分析，研究地铁暗挖隧道初期支护变形特性。崔凤［13］通过某工程实例介绍了浅埋暗挖法施工对临近建筑物的影响，并提出了相应的风险控制措施。

本文以哈尔滨地铁某区间隧道开挖工程为依托，利用大型通用岩土工程分析软件MIDAS／GTS建立隧道工程的有限元数值模型，将最后模拟结果得到的地表沉降结果与实际监测值吻合度进行分析，验证模型的合理性，在此基础上对隧道断面的变形进行分析，与此同时选取单洞与双洞两种施工工况，对隧道开挖的合理施工方法进行分析，为以后类似工程的施工提供参考。

1 工程背景

工农大街站—终点区间，从工农大街站开挖，顺丽江路向东前进通过半径3 m的曲线，至丽江路到达终点。区间起讫里程为DK42＋445．683—DK42＋869．516，区间全长 424．678 m，地层剖面图见图 1。区间隧道为矿山法施工，隧道竖向采用单向坡，最大坡度是1．51%，拱顶满身是15．20 m。两隧道之间的轴线距离是14 m，隧道初衬厚度为0．25 m，二衬支护厚度是0．30 m，见图2。

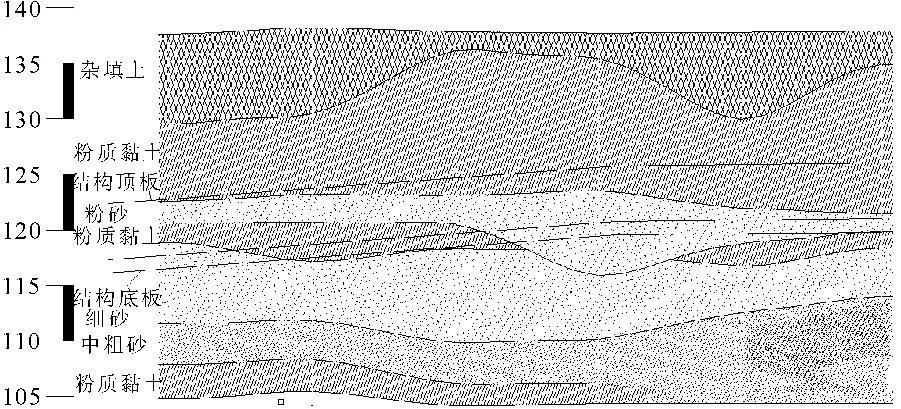
图1 地层剖面图

图2 隧道的断面图

2 数值模型的建立

2．1 基本假定

有限元模型中考虑以下基本假定：

（1）材料采用修正Mohr－Coulomb破坏屈服准则，考虑土体卸载和重加载刚度硬化。

（2）各土层均简化为匀质成层水平分布。

（3）本暗挖隧道的施工是在降水的前提下进行施工，无需考虑地下水渗流在隧道开挖过程中的影响。

2．2 单元类型及材料参数

隧道的围护结构选用弹性材料，隧道初衬采用三维板单元模拟，二衬支护结构采用修改单元属性的计算模块，通过设定特有边界修改单元属性。隧道的锁脚锚杆选用植入式桁架单元，并选用圆形断面，其刚度按照其轴向刚度等效。本模型根据场地地质特点，将场地土简化为四层，各层土的物理力学参数见表1。

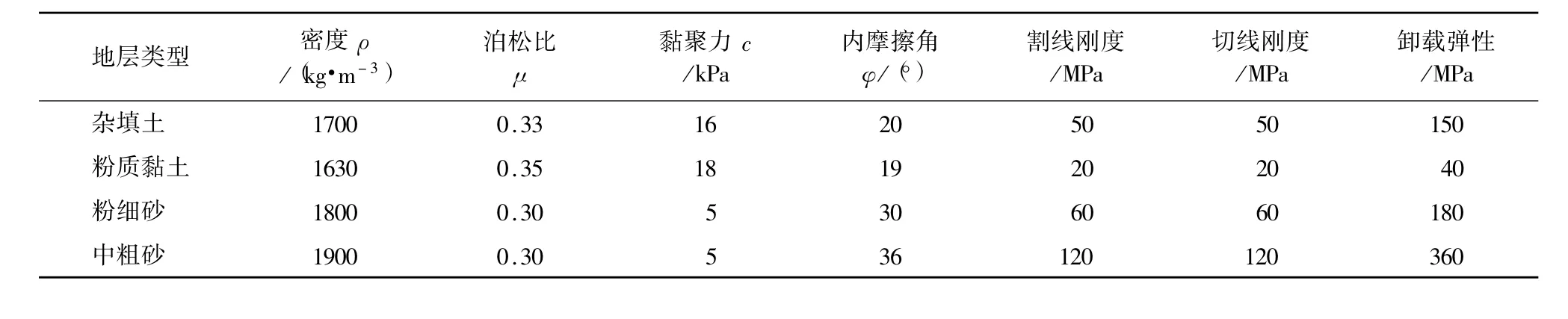
表1 土层参数表

2．3 计算模型

按照隧道开挖的影响范围大小，计算模型范围在水平和竖直方向取3～5倍隧道的跨度，向上取至地表。模型在水平方向取4倍的隧道开挖断面宽度，竖直方向从隧道底部开始取向下3倍洞径。有限元模型的长宽高分别取72 m×30 m×35 m。

模型的左右两侧约束水平方向的位移，底面约束水平和竖向方向上的位移，上表面为自由边界。土体材料均采用可考虑土体硬化和刚度与应力相关性的修正莫尔－库仑模型。该模型共有14 154个节点，13 960个单元。其计算模型见图3。

图3 有限元模型

3 数值模拟值与实际监测值对比分析

3．1 监测方案

针对隧道上方的地表沉降，沿轴线方向每隔50 m～100 m布置测点，并且地表测点顶部露出地表应控制在5 mm以内，见图4（a）。针对拱顶沉降，同一断面在拱腰部位布收敛测点，每间隔10 m布设一断面，见图 4（b）。

图4 监测点布置

3．2 结果对比分析

针对双线隧道施工过程中对地表沉降和水平收敛进行研究。选取左线隧道刚好贯通，右线隧道台阶开挖至15 m处的地表沉降量与实测地表沉降量进行对比。

3．2．1 地表沉降规律分析

（1）纵向地表沉降规律。图5是隧道施工过程中纵向地表沉降云图，由图5可知，沉降范围集中在左线隧道上部地表，沉降量从开挖初始至贯通结束逐渐减小，最大地表沉降量位于隧道洞顶，且左线隧道沉降范围大于右线。

图5 纵向地表沉降云图

开挖面不同距离的左、右线地表沉降模拟值和监测值的对比曲线见图6。为更好的反映地表沉降规律，对该监测断面点进行了加密布置，截面沿隧道开挖方向分别取左、右线隧道中轴线为剖面，获取地表沉降值。由图6可知，受隧道开挖时空效应的影响，开挖面以后地表沉降量大于开挖面前方未开挖处地表沉降量，开挖面前方未开挖10 m范围内为掌子面扰动影响区，开挖面1．5D外几乎不受掌子面开挖影响，沉降量控制在3 mm以内。隧道左线先开挖，纵向沉降量大于右线隧道纵向沉降量，最大沉降量为19．41 mm，右线最大沉降量为 18．51 mm，分析因为左线隧道沉降完全，右线隧道在后续施工过程中还会产生沉降，但由于左线隧道施工对右线为施工地层起到加固作用，故右侧沉降量小于左线。沉降监测值与计算值较为相近，说明模拟结果真实可靠，可用来预测相应模型。

图6 地表沉降的数值模拟值和监测值对比曲线

（2）横向地表沉降规律。图7是隧道施工过程中横向地表沉降云图，由图7可见，隧道横向沉降在双线隧道各自洞顶最大，向上地表延伸相互接合，左线隧道施工完毕，最大回弹量为6 mm，而右线隧道正处于施工阶段，核心土处回弹量最大，向下呈U形分布；在双线隧道地表中轴线处，呈现出拱形沉降等值线分布形式，隧道施工对上部土体沉降影响范围处于4D范围内。

图7 横向地表沉降云图

开挖面不同距离地表沉降值模拟值与沉降值的对比曲线见图8。距隧道中轴线约40 m范围内，横向方向取垂直于隧道开挖面为截面，分别选取距离施工面－12 m、－7 m、0 m、8 m、12 m处的实际监测结果与数值模拟结果进行对比分析。由图8可见，受隧道先后开挖顺序的影响，右线隧道开挖至12 m时，距开挖面0 m时，地表沉降曲线呈现出轴对称现象，并且最大沉降值偏向左边隧道，说明双线隧道开挖时，先施工的隧道引起的地表沉降量占总沉降量比例较大；开挖始发处（x＝－12 m）沉降最大，最大沉降量为13．1 mm，距开挖面－7 m处，最大地表沉降量为 －12．3 mm，施工面的最大沉降值为 11．4 mm；距开挖面8 m、12 m处为左线开挖右线未开挖段，沉降量产生在左线隧道之上，最大沉降量分别为－8．49 mm，－9 mm。选取开挖面前方监测点中的有效测点，把地表沉降观测值与计算值进行对比，图中散点为监测值，监测值与模拟值拟合良好。监测值略小于模拟值，这是由于在实际工程中，考虑了地层加固及支护作用，地表沉降量较计算值小。

图8 地表沉降的模拟值和监测值对比曲线

3．2．2 水平收敛分析

图9为双线隧道拱腰处水平收敛值。左线隧道顶部最大收敛值是4．2 mm，并且由隧道左上方向周围扩散；左线隧道拱腰处最大水平收敛值为4．15 mm，位于隧道拱腰处，从横断面沿纵向延伸，呈层状分布；左右线隧道之间产生轻微的水平收敛，最大水平收敛值为2．1 mm，分析由于受上覆土压力和隧道内部卸荷的影响，隧道出现了被挤压的现象，拱腰周围的土体向两侧发生移动。右线隧道最大水平收敛值为4．2 mm，水平收敛值从靠近隧道边缘向外侧地层逐渐减小；隧道顶部的最大水平位移是4．15 mm，横向上隧道顶部最大，向两边逐渐减小。

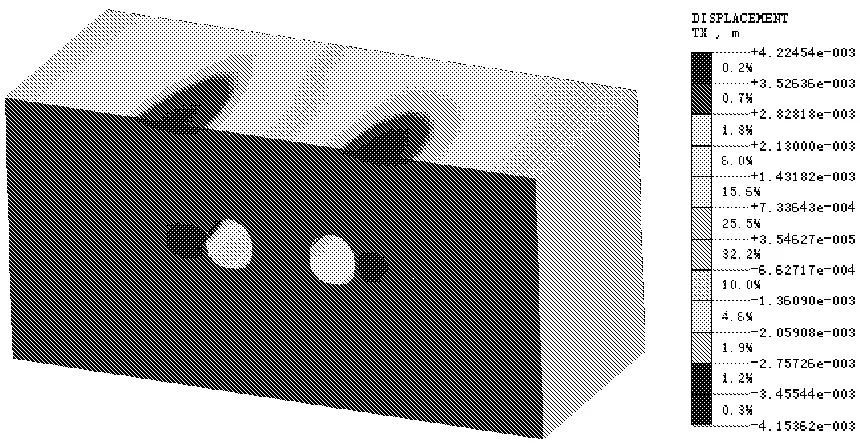
图9 双线隧道水平收敛云图

双线隧道地表水平位移和拱腰水平位移模拟值见图10。向隧道左侧的水平位移记为“－”，反之为“＋”。由图10可见，双线隧道、地表水平位移分别呈正弦分布规律，双线隧道水平位移方向与隧道顶部土体水平位移方向相反，呈8字型分布，由于隧道受上覆土体自重及内部土体卸荷作用，导致隧道土体向外侧发生变形，同时上部土体向下移动以弥补隧道水平位移产生的土体损失；双线隧道间土体的水平位移变形较小，左线隧道周围的土体向右移动，最大位移是2．1 mm，地表的最大水平位移与隧道水平位移几乎相同。

图10 隧道水平位移的模拟值

4 不同台阶长度对隧道纵剖面竖向位移的影响

为研究不同台阶长度对地层变形的影响，分别取0．5D、1．0D、1．5D、2．0D（D 为隧道开挖断面跨度，约6 m），隧道上、下台阶的高度取开挖面高度的一半。另外，由于实际施工中两隧道错距开挖距离较大，单隧道受台阶长度的影响同样十分重要。因此，分别对单个隧道和双洞隧道进行模拟分析。

（1）单线隧道施工。由图11的单个隧道竖向位移云图可以看出，台阶长度的不同对开挖面处上方地表沉降的影响较大，随着台阶长度的增加，其开挖面处上方地表沉降以及拱顶沉降也随之增大。针对四种施工工况，当上台阶的开挖面处于同一位置时，台阶长度为3 m（0．5D）的拱顶和地表沉降值最大，分别为13．2 mm和5．9 mm。当台阶长度为6 m（1．0D）时，拱顶和地表沉降量分别增大 8．3 mm（63%）和4．9 mm（83%）；而随着台阶长度的继续增加，台阶长度为 9 m（1．5D）和 12 m（2．0D）时，地表沉降和拱顶沉降值则趋于稳定，受台阶长度影响不明显，见图12。分析主要原因是由于台阶长度增加，衬砌闭合成环的时间变长，地层不能受到足够的衬砌结构约束而产生变形，进而引起地表沉降和拱顶沉降值增大。

图11 隧道纵剖面的竖向位移云图

图12 单个隧道不同台阶长度竖向位移曲线图

（2）双线隧道施工。由图13的双隧道竖向位移云图可以看出，受临近隧道开挖的影响，隧道地表沉降与拱顶沉降值均有不同程度的增长，隧道上台阶开挖面附近的土体影响较为明显。从云图上可以看出，隧道开挖面上方的土体受扰动范围较单个隧道工况有所扩大。与单个隧道相似，双隧道开挖在台阶长度对地层竖向变形影响规律相同。

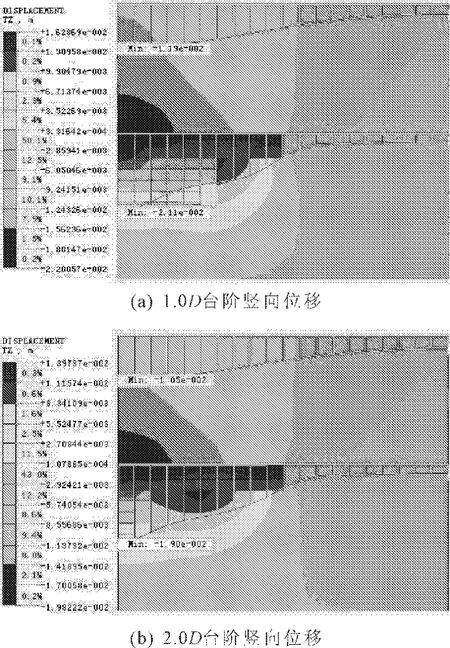
图13 隧道纵剖面竖向位移云图

5 结 论

论文采用MIDAS／GTS建立隧道施工的有限元分析模型，得到的数值分析结果与实际地表沉降监测值吻合程度较高，并基于此有限元模型得到以下分析结果：

（1）隧道纵向开挖面前方未开挖10 m范围内为掌子面扰动影响区，1．5倍洞径以外的几乎不受隧道施工的影响；隧道横向双线隧道地表中轴线处形成拱形沉降等值线分布形式，上部土体沉降影响范围处于4倍洞径范围内；

（2）双线隧道的最大水平位移出现在隧道外侧拱腰处，左右线隧道之间产生轻微的水平收敛，双线隧道、地表水平位移分别呈正弦分布规律且两者位移方向相反；

（3）开挖过程台阶长度增加，不论是单轴还是双轴隧道，在隧道纵轴方向均引起地表沉降和拱顶沉降值增大。

［1］ RB Peck．Deep excavations and tunneling in soft ground．State of Art Report Proc［C］／／7th Int．Conf．SMFE．Mexico：Mexico University Press，1969：225-290．

［2］ 何 桥，叶明亮，田 凯，等．浅埋暗挖隧道施工过程数值模拟分析［J］．水利与建筑工程学报，2015，13（6）：36-41．

［3］ 尚淑萍，胡玉娇，徐彦妮．基于既有线平顺性浅埋暗挖隧道地面沉降控制标准［J］．水利与建筑工程学报，2014，12（2）：95-99．

［4］ 陈利杰，张晓平，刘华斌，等．城市浅埋软岩隧道施工沉降分析及对策［J］．工程地质学报，2010，18（2）：281-288．

［5］ 陈星欣，白 冰．隧道下穿既有结构物引起的地表沉降控制标准研究［J］．工程地质学报，2011，19（1）：103-108．

［6］ 唐益群，叶为民，张庆贺．上海地铁盾构施工引起地面沉降的分析研究（三）［J］．地下空间，1995，15（4）：250-258．

［7］ Finno R，Clough G W．Evaluation of soil response to EPB shield tunneling［J］．Journal of Geotechnical Engineering，1985，111（2）：157-173．

［8］ 李 维，何 川，张志强．大型地下结构下修建盾构隧道模型试验［J］．西南交通大学学报，2005，40（4）：478-483．

［9］ 刘 波，叶圣国，陶龙光，等．地铁盾构施工引起邻近基础沉降的 FLAC数值模拟［J］．煤炭科学技术，2002，30（10）：75-80．

［10］ 赵华松，周文波，刘 涛，等．双线平行盾构施工引起的土体位移分及析其软件开发［J］．上海大学学报，2005，11（4）：516-421．

［11］ 杨福麟，刘永林，胡 斌．武汉地铁隧道开挖引起地表沉降的数值模拟研究［J］．工程地质学报，2013，21（1）：85-91．

［12］ 曹 波，刘 波，聂卫平．下穿既有电缆隧道的地铁暗挖隧道稳定性研究［J］．隧道建设，2013，33（11）：917-920．

［13］ 崔 凤．地铁区间浅埋暗挖施工对周边建筑安全的影响研究［J］．建筑技术，2017，48（3）：236-238．