基于罗德里格矩阵的抗差迭代坐标转换算法研究

李国琴，田林亚，郭英起，张 洋，毕继鑫

(1.河海大学 地球科学与工程学院，江苏 南京 210098；2.黑龙江工程学院 测绘工程学院，黑龙江 哈尔滨 150050；3.江苏苏州地质工程勘察院，江苏 苏州 215129)

对于不同基准下的空间直角坐标的转换，Bursa-Wolf模型、Molodensky模型和武测模型已得到广泛应用[1]，但是这三种模型主要适用于旋转角为小角度的特殊前提。在工业安装测量、盾构机导向测量、海底沉管测量等许多实际测量中，坐标转换时经常遇到大旋转角的情况，如果仍简单套用已有的坐标转换模型和算法，就可能得到错误的计算结果和结论。近些年，一些学者对大旋转角情况下的坐标转换问题做了较多的研究。同济大学陈义教授提出一种顾及旋转矩阵元素之间的相关性，利用附有限制条件的间接平差求取13个参数进行坐标转换的方法[2]；武汉大学曾文宪教授提出三维坐标转换的非线性模型，实现了旋转角在50°以内的坐标转换[3]；文献[4]～文献[5]研究了利用单位四元数法构造旋转矩阵进行坐标转换的方法；文献[6]～文献[7]将罗德里格矩阵引入到坐标转换中，无需进行繁琐的三角计算，但并未顾及公共点自身精度对坐标转换结果的影响；文献[8]将稳健抗差估计理论应用到坐标转换中，但该方法只适用于旋转角为小角度的坐标转换。本文提出一种基于罗德里格矩阵的抗差迭代算法，其主要思想：首先计算基于罗德里格矩阵坐标转换参数的初值，然后通过线性化模型计算转换参数的改正数，同时应用稳健抗差估计理论中的选权迭代法进行迭代计算，剔除含有粗差的公共点以及减小误差过大的点对转换结果的影响。该算法不仅同时适用小旋转角和大旋转角情况的坐标转换，而且可以有效抵抗可能存在的数据粗差对坐标转换结果的影响，计算模型简单，便于程序实现，收敛速度快，计算精度高，可在实际工作中推广应用。

1 基于罗德里格矩阵的抗差迭代坐标转换算法

1.1基于罗德里格矩阵坐标转换模型

文献[9]叙述了空间直角坐标转换模型，将罗德里格矩阵R代入到该转换模型中，可得到含有3个平移参数、3个反对称矩阵参数、1个尺度比参数的罗德里格矩阵坐标转换七参数模型，即

(1)

式中：下标q表示欲转换的目的坐标系，下标p表示原坐标系；λ为尺度比参数；ΔX，ΔY，ΔZ为三个平移参数；R为罗德里格矩阵，满足R=(I+S)(I-S)-1=(I-S)-1(I+S)，I为三阶单位阵，反对称矩阵S是由三个独立的未知数参数a，b，c组成，即

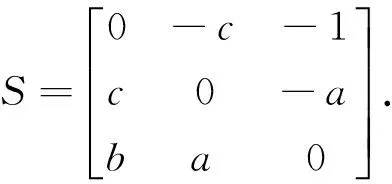
(2)

先对基于罗德里格矩阵的坐标转换模型进行线性化，即

(3)

其中，λ0为尺度比参数初值，R0为罗德里格矩阵初值，ΔX0，ΔY0，ΔZ0为三个平移参数初值，得到误差方程

(4)

可解得转换参数改正数

(5)

其中，

B11=B22=B33=1,

B12=B13=B21=B23=B31=B32=0,

B14=κ[(4ab2+4ac2)Xpi+(2a2b+4ac-2b-

2b3-2bc2)Ypi+(2c+2b2c+2c3-2a2c+4ab)Zpi],

B15=κ[(-4b-4a2b)Xpi+(2ab2+4bc-2a-

2a3-2ac2)Ypi+(2b2-2a2-2c2-4abc-2)Zpi],

B16=κ[(-4c-4a2c)Xpi+(4abc+2c2-2-

2a2-2b2)Ypi+(2a3+2a+2ab2-2ac2+4bc)Zpi],

B24=κ[(2a2b-2b-2b3-2bc2-4ac)Xpi-

(4a+4ab2)Ypi+(2a2-2b2-2c2+4abc-2)Zpi],

B25=κ[(2ab2-2ac2-4bc-2a3-2a)Xpi+

(4a2b+4bc2)Ypi+(2b2c-2a2c+4ab-2c3-2c)Zpi],

B26=κ[(2a2+2b2-2c2+4abc+2)Xpi+

(4b2c-4c)Ypi+(2bc2+4ac-2a2b-2b3-2b)Zpi],

B34=κ[(2b2c+2c3-2a2c-4ab+2c)Xpi+

(2b2+2c2-2a2+4abc+2)Ypi+(-4a-4ac2)Zpi],

B35=κ[(2a2-2b2+2c2-4abc+2)Xpi+

(2b2c-2a2c-4ab-2c3-2c)Ypi+(-4b-4bc2)Zpi],

B36=κ[(2ab2-2ac2-4bc+2a3+2a)Xpi+

(2bc2-2a2b-2b3-4ac-2b)Ypi+(4a2c+4b2c)Zpi],

B17=κ[(1+a2-b2-c2)Xpi-(2ab+2c)Ypi+

(-2b+2ac)Zpi],

B27=κ[(2c-2ab)Xpi+(1-a2+b2-

c2)Ypi-(2a+2bc)Zpi],

B37=κ[(2ac+2b)Xpi+(2a-2bc)Ypi+

(1-a2-b2+c2)Zpi].

为了实现基于罗德里格矩阵坐标转换，需要模型参数初值计算。首先，计算尺度比参数λ的初值。可以通过位于两套坐标系的两个公共点的坐标进行计算，即

(6)

当含有多个公共点时，可以分别求取各公共点对应的边长之比，然后取其平均值计算尺度比参数初值。其次，求取3个反对称矩阵参数的初值，将位于两套坐标系下的公共点1和公共点2的坐标分别代入式(1)，做差可消去三个平移参数，得

(7)

其中，

Xq21=Xq2-Xq1，Yq21=Yq2-Yq1，

Zq21=Zq2-Zq1,

Xp21=Xp2-Xp1，Yp21=Yp2-Yp1，

Zp21=Zp2-Zp1.

根据反对称矩阵S和罗德里格矩阵R的关系，可得

(8)

将(I+S)，(I-S)代入，可得

(9)

式(9)中的系数阵为奇异阵，无法解出参数a，b，c初值的唯一解。因此，再将位于两套坐标系下的公共点3代入式(1)，并与公共点1代入式(1)的结果做差，联立式(9)得

(10)

对式(10)，采用最小二乘法得到反对称矩阵参数a，b，c的初值，进而得到罗德里格矩阵的初值R0。最后，将位于两套坐标系下的公共点1的坐标代入式(1)，可求出三个平移参数ΔX，ΔY，ΔZ的初值(也可以利用多个公共点通过式(8)计算三个平移参数，然后取其平均值)，即

(11)

1.2 基于稳健抗差估计理论的选权迭代

根据现代平差理论，经典最小二乘法不具有抗干扰性和抵抗粗差的能力[10]。如果所选择使用的公共点中某个点精度较低或误差过大，势必会影响转换参数的解算精度，进而会影响坐标转换的精度[8]。因此，本文将稳健抗差估计理论应用到基于罗德里格矩阵的坐标转换模型中，以达到抵抗粗差对坐标转换精度影响的目的。

将参数初值加上求解的七个转换参数改正数后，坐标转换即可进行。坐标转换后可以获得公共点的坐标差值，坐标差值的大小可以反映转换参数精度的高低。如果在解算坐标转换参数时公共点中的某个点精度较低，那么坐标转换后该公共点的坐标差值会比其它公共点的坐标差值更大，根据稳健抗差估计理论，可通过式(12)对公共点重新定权，从而降低精度较低的公共点对降低坐标转换精度的影响。

(12)

2 模拟计算与分析

现模拟一套数据作为算例进行计算与分析。设一个空间直角坐标系下有4个点p1～p4，现将这些点绕X轴，Y轴，Z轴分别旋转20°，30°，35°，再沿X轴，Y轴，Z轴分别平移230 m，170 m，75 m，设尺度比λ=1，最终得到在新坐标系下4个点q1～q4的坐标，各点的坐标数据如表1所示。

方案1：选取点1，2，3作为公共点，计算基于罗德里格矩阵坐标转换的初值，然后将这些初值代入坐标转换模型(1)中，对原坐标系中的4个点p1，p2，p3，p4进行坐标转换，计算转换后的坐标与新坐标系下点q1，q2，q3，q4的坐标差值，记为|Δ1|，再计算其点位偏差，记为m1，见表2。完成基于罗德里格矩阵坐标转换参数初值的计算后，将7个初值代入到基于罗德里格矩阵坐标转换线性化模型(3)，可得到误差方程式(4)，利用最小二乘法解算7个转换参数的改正数，然后将7个转换参数初值加上各自的改正数后再代入式(1)，对原坐标系中的4个点p1，p2，p3，p4进行坐标转换，计算转换后的坐标与新坐标系下点q1，q2，q3，q4的坐标差值，记为|Δ2|，再计算其点位偏差m2，见表2。

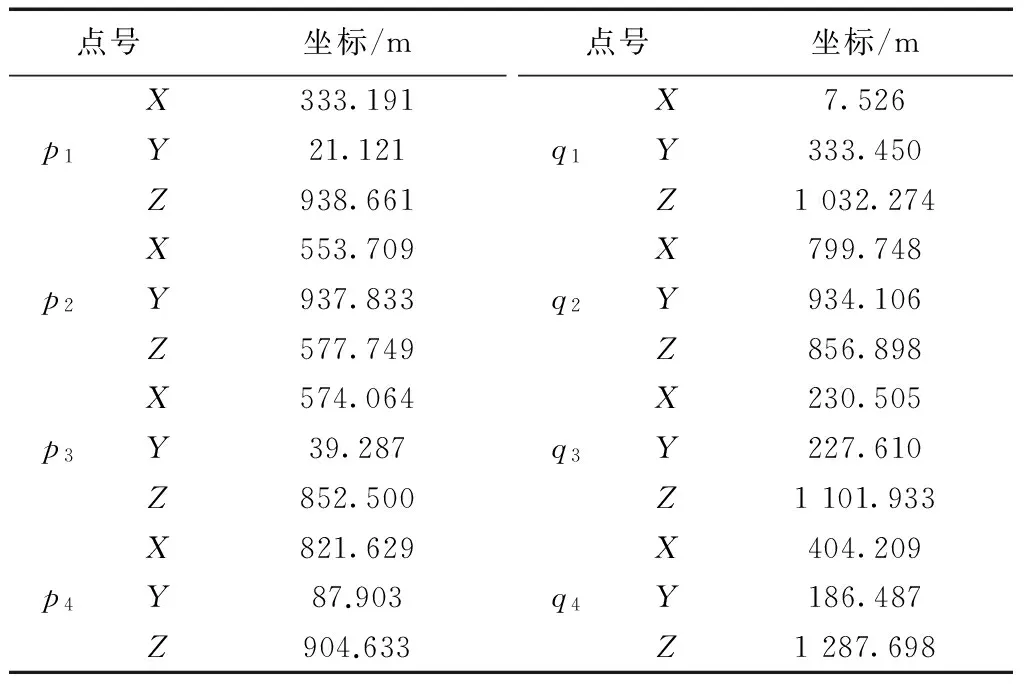
表1 已知点坐标数据

方案2：对原坐标系下点p1，分别在X，Y，Z方向加入1 cm，2 cm，2 cm的粗差，然后选取点1，2，3作为公共点，首先通过传统的基于罗德里格矩阵坐标转换模型对原坐标系中的4个点p1，p2，p3，p4进行坐标转换，计算转换后的坐标与新坐标系下点q1，q2，q3，q4的坐标差值，记为|Δ1|，再计算其点位偏差，记为m1，见表2。采用本文所述基于罗德里格矩阵的抗差迭代坐标转换模型，对原坐标系中4个点p1，p2，p3，p4进行坐标转换，计算转换后的坐标与新坐标系下点q1，q2，q3，q4的坐标差值，记为|Δ2|，再计算其点位偏差m2，见表2。

1)方案1分析。对比两次计算所得的各点的点位偏差可知，仅利用计算所得的罗德里格坐标转换模型七参数初值进行坐标转换，所得结果精度很低，而通过七参数初值和采用线性模型计算其参数的改正数，并将改正数与初值融合后再进行坐标转换，精度显著提高。事实上，利用最小二乘原理进行迭代计算所得到的转换参数改正数的效果会更好，由于篇幅有限，本文不再陈述。

2)方案2分析。由于p1点精度低、误差过大，相较于方案1中的第二种算法，各点坐标转换后的点位偏差明显变大，尤其是p1点转换后的点位偏差最大。综合分析表2中方案2的m1和m2，可见采用稳健估计原理进行坐标转换，除了p1点外，其它各点坐标转换后的点位偏差都减小了。对于点p1，虽然其点位偏差变大了，但其实它是更接近于该点真实值的。

3 结束语

本文将罗德里格矩阵和稳健抗差估计理论综合应用于空间直角坐标转换，研究适用于任意旋转角的空间直角坐标转换的抗差迭代算法，采用C#语言进行了编程实现，利用仿真数据和算法程序进行实验计算与分析。方案1的两次计算结果表明在无粗差情况下，利用罗德里格矩阵坐标转换线性化模型计算转换参数改正数后再进行坐标转换，相较于直接利用转换参数初值进行坐标转换的精度会明显提高。方案2的两次计算结果表明在公共点含粗差情况下，将稳健抗差估计方法应用于基于罗德里格矩阵的坐标转换是可行的，能够有效地抵抗粗差对转换结果的影响。

表2 各点转换后坐标差值及其点位偏差 cm

[1] 刘大杰，施一民，过静珺. 全球定位系统(GPS)的原理与数据处理[M]. 上海：同济大学出版社，1999.

[2] 陈义，沈云中，刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报(信息科学版)，2004，29(12)：1101-1104.

[3] 曾文宪，陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报(信息科学版)，2003，28(5)：566-568.

[4] SCHENK T. From Point Based to Feature-Based Aerial Triangulation[J]. ISPRS Journal of Photogrammetry & Remote Sensing，2004(58)：315-329.

[5] 姜柱，刘庆元，周曼. 单位四元数在坐标转换中的应用[J]. 矿山测量，2012(5)：28-30.

[6] 韩梦泽，李克昭. 基于罗德里格矩阵的空间坐标转换[J]. 测绘工程，2016(4)：25-27.

[7] 杨凡，李广云，王力，等. 一种基于罗德里格矩阵的最小二乘迭代坐标转换方法[J]. 工程勘察，2010(9)：80-84.

[8] 郭英起，唐彬，张秋江，等. 基于空间直角坐标系的高精度坐标转换方法研究[J]. 大地测量与地球动力学，2012(2)：125-128.

[9] 潘国荣，赵鹏飞. 基于空间向量的三维基准转换模型[J]. 大地测量与地球动力学，2009(6)：79-82.

[10] 黄维彬. 近代平差理论及其应用[M]. 北京:八一出版社，1992.