低空机载LiDAR点云定位误差分析
杜 婷,李 浩,杨 彪,苏 博,刘亚南
(河海大学 地球工程与工程学院,江苏 南京 211100)
近年来,随着无人机等摄影硬件平台技术的逐步成熟,一种新型、快捷的遥感系统——低空机载LiDAR系统应运而生。与传统摄影测量相比,该系统因其具有较强的植被穿透能力,能更直接、高效获取地面高精度点云数据;与传统机载LiDAR技术相比,其灵活的飞行平台、相对较低的硬件成本具有显著优势。因此,该系统在地形测量、防灾减灾、工程设计、地质勘查、林业资源调查等多领域具有广阔的应用前景,并已取得了一些实质的研究成果[1-4]。
低空机载LiDAR系统的定位精度问题是该系统生产应用关心的核心问题。目前,LiDAR系统的定位精度评价主要集中在传统机载LiDAR领域。为了定量分析点云的定位误差,各种严格的LiDAR点云定位误差模型已被提出。Schenk总结主要误差源推导出系统误差方程[5],张小红根据Schenk的误差模型,详细推导了系统误差公式[6]。然而,不同于传统机载LiDAR,现有低空机载LiDAR系统普遍采用低成本POS装置,飞行平台稳定性也相对较差,其得到的点云误差精度相对较低[7-9],因此怎样通过设置飞行参数来保证精度是个难题。
为此,本文紧密结合现有低空LiDAR技术水平,分析航高、扫描角、IMU姿态角及其误差、安置角误差等主要因素对点云定位精度的影响,并探讨了其影响规律,旨在为该系统的实际生产应用提供建议。
1 低空机载LiDAR系统组成及其主要误差来源
低空LiDAR系统组成部分:
1)低空遥感平台:包括载人小型直升机、动力三角翼、气艇、旋翼无人机、固定翼无人机;通常飞行高度小于1 000 m,云下作业。
2)低空机载LiDAR扫描仪:按扫描原理分为有摇摆式扫描系统、旋转多棱镜扫描系统、光钎扫描系统三种。
3)POS装置:包括GPS和IMU(IMU- Intertial Measurement Unit,惯性导航单元)。GPS设备通过实时差分或事后差分得到传感器平台的空间位置,IMU用于精确测定传感器平台的空间姿态角。
4)其它装置:包括数码相机、航线规划与飞行控制器、系统供电装置等;
由于低空机载LiDAR组成复杂,点云精度受很多因素影响,如IMU姿态角、姿态角误差、偏心误差等,其中偏心误差是各仪器坐标系之间的平移误差,一般来说,这种误差在解算时可以消除,带来的影响不大,所以在本文的分析中忽略偏心误差。
根据《CHZ 3005-2010低空数字航空摄影规范》,目前低空LiDAR系统的主要影响参数见表1。

表1 现有低空LiDAR系统主要参数
2 低空机载LiDAR点云定位误差模型
低空机载LiDAR系统是集成了多种先进技术的复杂系统,具体包括:测定摄影中心位置方位元素的动态GPS接收机系统;测定摄影中心姿态参数的姿态测量系统(IMU系统);测定传感器到地面点距离的机载激光雷达测距系统等,各个系统之间定义的坐标系如图1所示。

图1 机载激光雷达系统坐标系
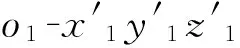
根据LiDAR激光测距仪测得的斜距ρ,POS系统记录的飞行位置和姿态参数,以及各个坐标系统之间的转换关系,推导出激光脚点定位方程[2]:
PW=PGPS+RIMU(RluRlbs+l0).
(1)
其中,PW是激光点在WGS-84中的坐标,PGPS是GPS天线相位中心在WGS-84中的坐标,RIMU是IMU姿态角旋转矩阵,Rlu为安置角旋转矩阵,Rlb为瞬时激光扫描系到激光扫描参考系的旋转矩阵,s=(0,0,ρ)为激光脚点在瞬时激光扫描系的坐标,l0为GPS天线相位中心的偏心改正。
由于机载激光雷达扫描系统本身受到来自激光测距、姿态、飞行器位置等各种误差的影响,在误差相互独立的情况下,对定位方程进行线性化:
(2)

式中:dX,dY,dZ为点云定位误差分量,dXG,dYG,dZG为GPS定位误差,Δx,Δy,Δz为偏心误差。
由式(2)根据误差传播定律得
(3)
式中:mx是定位误差X分量中误差,mρ,mθ,mΔκ,mΔφ,mΔω,mH,mP,mR,mΔx分别是定位误差影响因素的中误差。定位误差Y分量中误差my、定位误差Z分量中误差mz形式与式(3)类似。
3 低空机载LiDAR点云定位误差分析
低空机载LiDAR系统组成复杂,点云精度受很多因素影响,为了对点云定位误差进行定量分析,假设这些误差之间是不相关的,分别改变式(2)中的单个变量大小分析该变量的误差对最终定位精度的影响,点云定位误差与各个误差的关系如图2所示。其中m为定位中误差,mx,my,mz分别为X方向中误差、Y方向中误差、Z方向中误差。
当航偏角、俯仰角、侧滚角皆为10°,最大扫描角60°,最大飞行高度1 000 m,按表1取航偏角中误差0.1°,俯仰角、侧滚角中误差0.03°,安置角中误差0.005°,扫描角中误差0.005°,测距中误差0.1 m时,各因素对定位误差的影响分析。
3.1 航高对点云定位误差的影响
保持其他参数不变的情况下,航高从0~1 000 m引起的定位误差的变化如图2(a)所示。在其他参数不变的情况下,航高与定位误差之间的关系近似是线性的。
3.2 扫描角对点云定位误差的影响
保持其他参数不变的情况下,扫描角从-60°~60°,引起的定位误差的变化如图2(b)所示。从图中可以看出,在其他参数不变的情况下,扫描角大于0°时,扫描角越大,X,Z定位误差越大。
3.3 IMU姿态角大小对点云定位误差的影响
1)航偏角的影响。保持其他参数不变的情况下,航偏角从0°~15°变化时的定位误差如图2(c)所示。在其他参数不变的情况下,航偏角的变化对高程定位误差没有明显的影响,航偏角越大,X定位误差越大。
2)俯仰角的影响。保持其他参数不变的情况下,俯仰角从0°~15°变化时的定位误差如图2(d)所示。在其他参数不变的情况下,俯仰角的变化定位误差没有明显的影响。
3)侧滚角的影响。保持其他参数不变的情况下,侧滚角从0°~15°变化时的定位误差如图2(e)所示。在其他参数不变的情况下,侧滚角的变化与定位误差近似呈线性关系。
3.4 姿态角误差对点云定位误差的影响
姿态角测量误差主要影响因素为脱落漂移误差、加速度计比例误差、速度计常数误差等[12]。
1)航偏角误差的影响。保持其他参数不变的情况下,航偏角为10°时,其误差从0°~0.1°变化时的定位误差如图2(f)所示。在其他参数不变的情况下,航偏角误差的变化对定位误差没有明显的影响。
2)俯仰角误差的影响。保持其他参数不变的情况下,俯仰角为10°时,其误差从0°~0.05°变化时的定位误差如图2(g)所示。在其他参数不变的情况下,航偏角误差的变化与定位误差近似成线性关系。
3)侧滚角误差的影响。保持其他参数不变的情况下,侧滚角为10°时,其误差从0°~0.05°变化时的定位误差如图2(h)所示。在其他参数不变的情况下,侧滚角误差的变化与定位误差近似成线性关系。
3.5 安置角对点云定位误差的影响
由于三个安置角对定位误差的影响是类似的,本文分析一个安置角。保持其他参数不变的情况下,安置角从0°~0.01°变化时的定位误差如图2(i)所示。在其他参数不变的情况下,安置角误差的变化对定位误差没有明显的影响。
3.6 不同比例尺下的低空LiDAR作业参数的选择
对各项误差的分析,航高、扫描角、侧滚角误差对最终定位误差的影响较大,基本是呈线性递增的关系,侧滚角误差通过仪器制造商改正,实际作业时控制飞行航高和扫描角的大小即可以改善点云定位精度。
实际作业时,由相关测图比例尺要求限制最终的定位误差,参照误差模型综合分析图2反推相应的飞行航高和扫描角,不同测图比例尺要求下作业参数如表2所示。

表2 不同比例尺作业参数

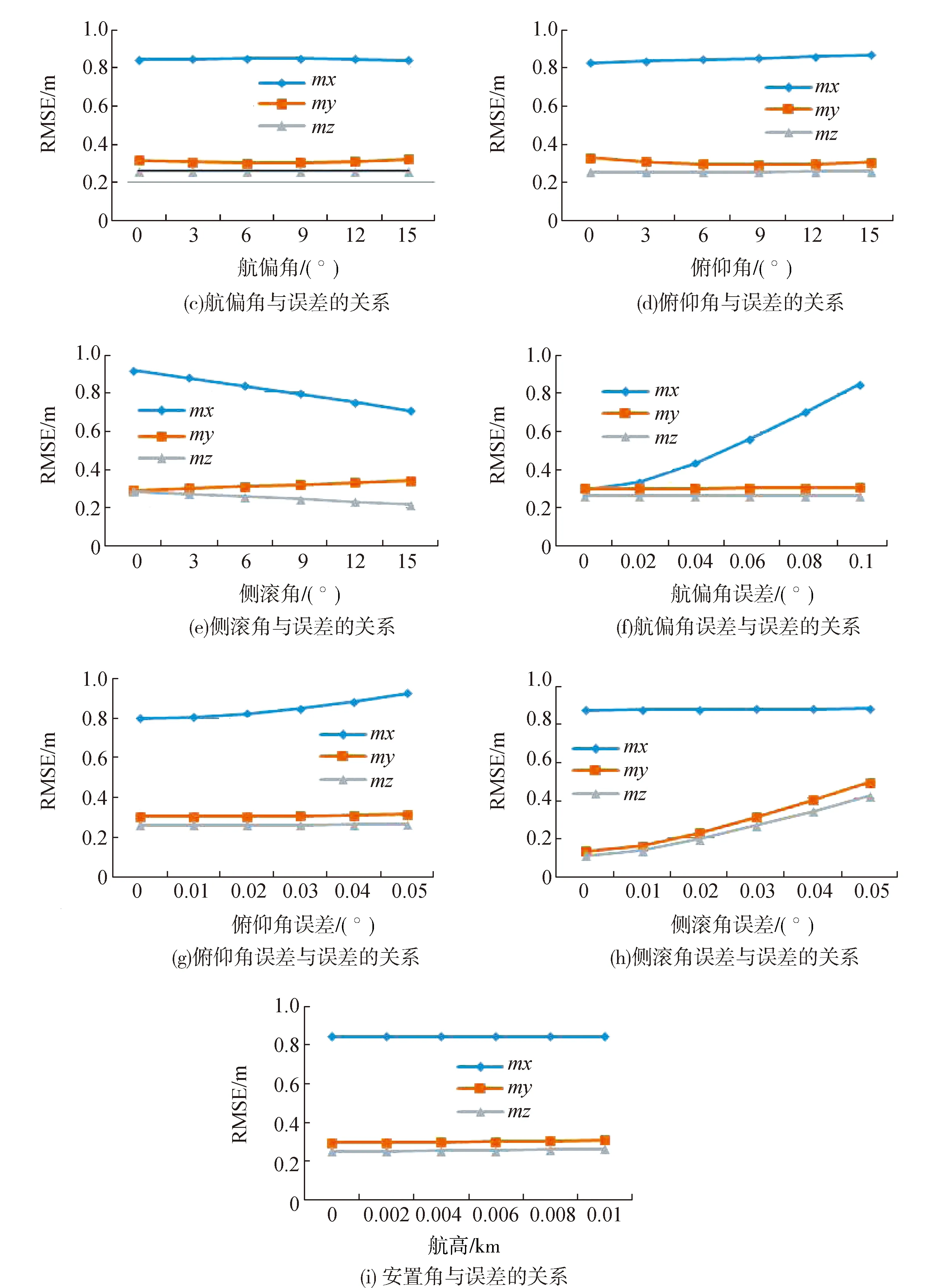
图2 不同误差对点云定位误差的影响
4 实验与分析
2015年10月,实验选取长江河道江西九江至湖口张家洲河段为试验区,采用动力三角翼搭载激光雷达及数码相机同步进行数据采集,累计施测面积达60 km2。三维激光扫描系统为HawkScan1200(如图3所示),系统的姿态角解算误差为航偏角误差为0.1°,俯仰角和侧滚角误差为0.03°。根据1∶2 000地形图航空摄影测量数字化测图规范按照表2作业参数设置相对航高约为500 m,飞行速度约100 km/h,扫描角范围为-45°~45°。共采集29 587 722点,平均点云密度为:0.5点/m2。扫描区域的采集点云如图4所示。

图3 动力三角翼与HawkScan1200系统
根据采用仪器的参数代入误差模型计算定位中误差的理论值,计算得到该点云数据的平面中误差和高程中误差分别在0.270~0.847 m,0.104~0.120 m。

图4 点云数据
从高程中误差和平面中误差两方面来评价点云的实际定位误差。对于高程误差,选取道路中心、大堤两侧平坦地面、水平房顶等局部较为平坦的地表高程作为验证高程,利用GPS-RTK在现场放样出点的实际高程,将其与点云高程对比,并统计高程中误差;对于平面误差[10-11],由于LiDAR点云分布不规则,在LiDAR点云中难以像在高分辨率影像中那样可精确选取控制点和连接点,所以需要根据测区中的建筑物墙面相交拟合两条直线相交,取直线交点为建筑物角点,然后和实测建筑物角点进行对比,得到平面坐标误差。实验共选取3个验证区,点云相应的实际定位误差如表3所示。
根据表3实际点云定位误差均在计算的理论精度范围内,故该实验的实际作业精度符合作业规范。

表3 点云实际定位精度
5 结束语
本文根据低空机载LiDAR点云定位误差模型和目前商用低空LiDAR系统的性能,定量分析了航高、扫描角、IMU姿态角、姿态角误差及安置角误差对点云定位误差的影响,得出结论:
1)扫描角和航高是影响点云定位误差的主要因素,其对点云定位误差的影响基本呈线性递增关系;
2)本文研究的低空LiDAR的相关飞行参数符合相应比例尺要求下的点云精度要求,例如根据目前商用低空LiDAR系统的参数,按照飞行高度为500 m,扫描角度为45°内扫描的点云精度可以满足1∶2 000测图比例尺的要求。
[1] 许晓东, 张小红, 程世来. 航空Lidar的多次回波探测方法及其在滤波中的应用[J]. 武汉大学学报(信息科学版), 2007, 32(9):778-781.
[2] 鲁林, 周小成, 余治忠, 等. 随机森林算法在机载LiDAR数据林分平均树高估算中的应用研究[J]. 地球信息科学学报,2016,18(8):1133-1140.
[3] 陈功, 程正逢, 石克勤,等. 激光雷达在电力线路工程勘测设计中的应用[J]. 电力勘测设计, 2006(5):53-56.
[4] 杨颖, 朱磊, 张省,等. 直升机载LIDAR测量技术在高速公路改扩建勘测中的应用[J]. 地理信息世界, 2015, 22(5):104-107.
[5] SCHENK T. Modeling and recovering systematic errors in airborne laser scanners[J].Proceedings of OEEPE Workshop on Airborne Laser Scanning and Interferometer SAR for Detailed Digital Elevation Models, 2001: 40-48.
[6] 张小红. 机载激光雷达测量技术理论与方法[M]. 武汉: 武汉大学出版社, 2007: 66-72.
[7] 刘经南, 张小红, 李征航. 影响机载激光扫描测高精度的系统误差分析[J]. 武汉大学学报(信息科学版), 2002, 27(2):111-117.
[8] 熊爱武, 杨蒙蒙. 机载LiDAR点云数据误差分析[J]. 测绘通报, 2014(3):75-78.
[9] 李峰, 崔希民, 刘小阳,等. 机载LIDAR点云定位误差分析[J]. 红外与激光工程, 2014, 43(6):1842-1849.
[10] JIANG L F, TIAN L, GU Mei-Xia, et al. Effects of laser beam divergence angle on airborne LIDAR positioning errors[J]. Journal of Beijing Institute of Technology, 2012, 21(2):278-284.
[11] HUGENHOLTZ C H, WHITEHEAD K, BROWN O W,et al. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model[J]. Geomorphology, 2013, 194(4):16-24.
[12] LIN Y, HYYPPA J,JAAKKOLA A.Mini-UAV-borne LIDAR for fine-scale mapping[J]. IEEE Geoscience & Remote Sensing Letters, 2011, 8(3):426-430.
[12] 覃昕垚, 张建军, 王勇,等. 机载LiDAR定位精度分析[J]. 测绘工程, 2016, 25(5):32-35.

