方差分量估计的抗差总体最小二乘算法

陶叶青，蔡安宁，杨 娟

(淮阴师范学院 城市与环境学院，江苏 淮安 223300)

为解决变量中误差的模型参数 (errors-in-variables, EIV)估计问题，最小二乘约束准则(least squares estimation, LS)被拓展为总体最小二乘约束准则(total least squares estimation, TLS)[1]。应用总体最小二乘约束准则建立模型参数估计算法受到研究人员的关注，此算法可以使总体最小二乘参数估计模型被应用到坐标相似变换[2-9]、高程异常拟合[10]、大地测量反演[11]等测量数据处理中。

研究人员在讨论模型参数估计算法的同时，将经典平差模型中存在的粗差处理问题引入到总体最小二乘模型中进行讨论[12-18]。文献[12]应用粗差识别理论阐述总体最小二乘模型粗差处理的方法，但是算法没有通过实例进行验证。基于粗差调节理论，应用等价权函数建立的抗差总体最小二乘算法(robust total least squares, RTLS)是处理含有粗差的EIV模型的主要方法：文献[13]基于Huber权函数，应用高斯-赫尔墨特模型(Gauss-Helmert model, G-H)建立总体最小二乘抗差迭代算法，并将其应用至空间坐标系统转换；随后，文献[14]～[18]分别基于不同的权函数，应用极值函数建立含有粗差的总体最小二乘模型抗差估计算法。

研究人员采用经典平差模型的粗差处理思路解决总体最小二乘模型的粗差处理问题，需要注意的是含有粗差的总体最小二乘模型具有显著的特征，其研究思路不能完全趋同于最小二乘模型。此类问题引起研究人员的关注：总体最小二乘模型系数矩阵与观测向量可能由不同类型的观测元素组成，直接通过观测值的改正数调节权值的抗差算法，在文献[19]～[21]得到改进。文献[19]借助标准化残差，文献[20]借助敏感度分析构造统计量，增加抗差总体最小二乘算法的通用性。同时，总体最小二乘模型是非线性模型，在有限观测元素条件下，得到的单位权中误差是有偏的[3]。文献[7]建立了单位权中误差无偏估计的迭代算法，但是没有顾及含有粗差的观测值对估值的影响。此外，当模型的系数矩阵与观测向量由不同类型的观测元素组成时，由相同的中误差确定权函数的域值是不合理的。为合理确定等价权函数中分段函数的域值，中位数法被应用在抗差总体最小二乘估计[21]。现有研究成果是假定随机模型是精确、已知的，缺乏当随机模型存在偏差对抗差算法影响的探讨。

为顾及随机模型误差对总体最小二乘抗差估计的影响，有效应用等价权函数实现抗差估计，本文讨论采用方差分量估计(variance component estimation, VCE)[22]修正随机模型，通过最小二乘方差分量估计(least squares variance component estimation, LS-VCE)的总体最小二乘参数估计迭代算法[23]，分别计算系数矩阵与观测向量的中误差。在应用权函数对观测元素进行迭代定权的同时，对随机模型进行修证，分类确定不同类型观测值对应权函数的域值。

1 抗差总体最小二乘估计

总体最小二乘准则能够同时对系数矩阵与观测向量中含有的误差附加约束：

(1)

式中：Δ为观测向量L中含有的误差向量，EB为系数矩阵B中含有的误差矩阵，x为参数向量，b=vec(EB)(vec(·)为矩阵拉直符号，表示将误差矩阵按列拉直，得到列向量)；P，PB为观测向量与系数矩阵的权矩阵，其中PB可以由协因数阵的Kron积得到，具体定义过程请参见文献[3]。需要指出的是，对于partial-EIV模型[24]系数矩阵中常数元素的定权问题，可以通过协因数阵的定义来解决。

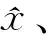
(2)

(3)

式中：A0为拉格朗日函数关于参数向量的偏导数，x0为参数向量的初值，ω0=L-Bx0，B10为拉格朗日函数关于误差向量Δ的偏导数，B20为关于误差向量b的偏导数，N是关于B10与B20的函数，λ为拉格朗日乘数，Q1为参数向量的协因数阵，Q2为系数矩阵的协因数阵。模型参数的具体求解方法请参见文献[15]。根据系数矩阵与观测向量中残差的估值，应用等价权函数对观测元素进行重新定权，以IGGⅡ权函数为例[25]

(4)

抗差总体最小二乘参数估计的研究思路与经典平差模型的抗差估计研究思路趋于一致，其优点是理论基础成熟、算法容易实现，但是忽略了总体最小二乘模型与最小二乘模型之间的差异。在总体最小二乘模型中，当系数矩阵与观测向量中的元素不属于同一类观测值时，两者在精度上往往不属于同一量级，并且随机模型的定义存在偏差。此时，通过单一的中误差统一确定观测值的权，这样的方法显然是不合理的。有学者提出“附有相对权比”[26]、“标准化残差”[19]等方法来克服传统算法存在的问题，但是并不能够消除随机模型误差对参数估计的影响。由此，论文探讨应用方差分量估计建立总体最小二乘抗差估计算法。

2 基于方差分量估计的抗差算法

2.1 方差分量估计的最小二乘算法

方差分量估计是进行随机模型验后估计的有效方法，一直受到研究人员的关注，主要算法有赫尔默特方差估计、最小范数二次无偏估计(MINQUE)、最优不变二次无偏估计(BIQUE)。最小二乘方差分量估计被证明优于其它方差估计算法[22]，应用LS-VEC改正总体最小二乘随机模型，在此基础上建立抗差总体最小二乘参数估计的迭代算法。当不顾及系数矩阵中的误差，EIV模型退化为高斯-马尔可夫模型(Gauss-Markov model, G-M)

Δ=Bx-L.

(5)

设观测向量L对应的协方差阵为D(l)，将其表示为观测元素中误差的函数

(6)

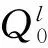
(7)

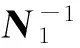
(8)

(9)

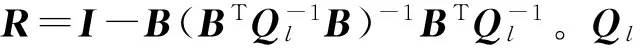
2.2 抗差总体最小二乘的迭代算法

EIV模型系数矩阵B对应的协方差阵为D(B)，将其表示为系数矩阵中观测元素的中误差函数

(10)

应用LS-VEC建立抗差总体最小二乘迭代算法：

2)应用式(6)、式(10)计算观测向量与系数矩阵的协因数阵Ql，QB；

3)根据式(2)、式(3)计算EIV模型的总体最小二乘解，以及系数矩阵与观测向量中误差向量的估值，并用其对观测向量与系数矩阵进行改正，由改正后的观测向量、系数矩阵与调节后的协因数阵计算正交投影矩阵R，元素nij，li，以确定N1，l1，并且应用式(7)计算待估向量σk；

4)应用权函数对观测元素进行分类定权。需要指出的是，当EIV模型的观测向量与系数矩阵中的观测元素属于不同的精度类型，权函数的域值也可以采用标准化残差[19]、敏感度分析[20]、中位数法[21]等进行分类确定；

5)迭代步骤(2)、(3)、(4)，直到参数估值收敛。

3 算例与分析

应用直线拟合对建立的算法进行验证，当有n个观测值时，将直线方程表示为

(11)

式中：[kb]T为模型待估参数向量。应用文献[27]的数据作为实验数据，见表1。

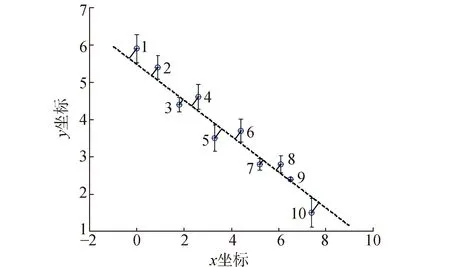
图1 参数最优估值的拟合精度

应用上述观测数据对论文建立的算法进行验证，分别在1号点的x坐标、3号点的y坐标中加入1个单位的误差，模拟观测值中含有的粗差；并且将求解参数的元素分为三组：一组(1，2，4，…，10)，二

组(2，3，4，…，10)，三组(1，2，3，…，10)，分别模拟模型系数矩阵中的元素含有粗差，模型观测向量中的元素含有粗差，模型观测向量与系数矩阵中的元素同时含有粗差的三种情况。应用基于等价权函数的抗差总体最小二乘传统算法，不同观测样本求解的参数估值见表2。需要指出的是，三组样本获得的残差改正数均小于权函数中第一个分段函数的域值，这显然是和实际情况相违背的，权函数没有对随机模型进行调节。三组样本拟合的精度见表3。

表2 模型参数的估值

基于方差分量估计的抗差算法，对系数矩阵元素与观测向量元素分类确定权函数的域值，求解模型参数估值。经过四次迭代计算，获得参数的估值见表2，其拟合精度见表3，等价权函数能够对随机模型进行有效的调节。

两种算法拟合精度的误差分布如图2所示。

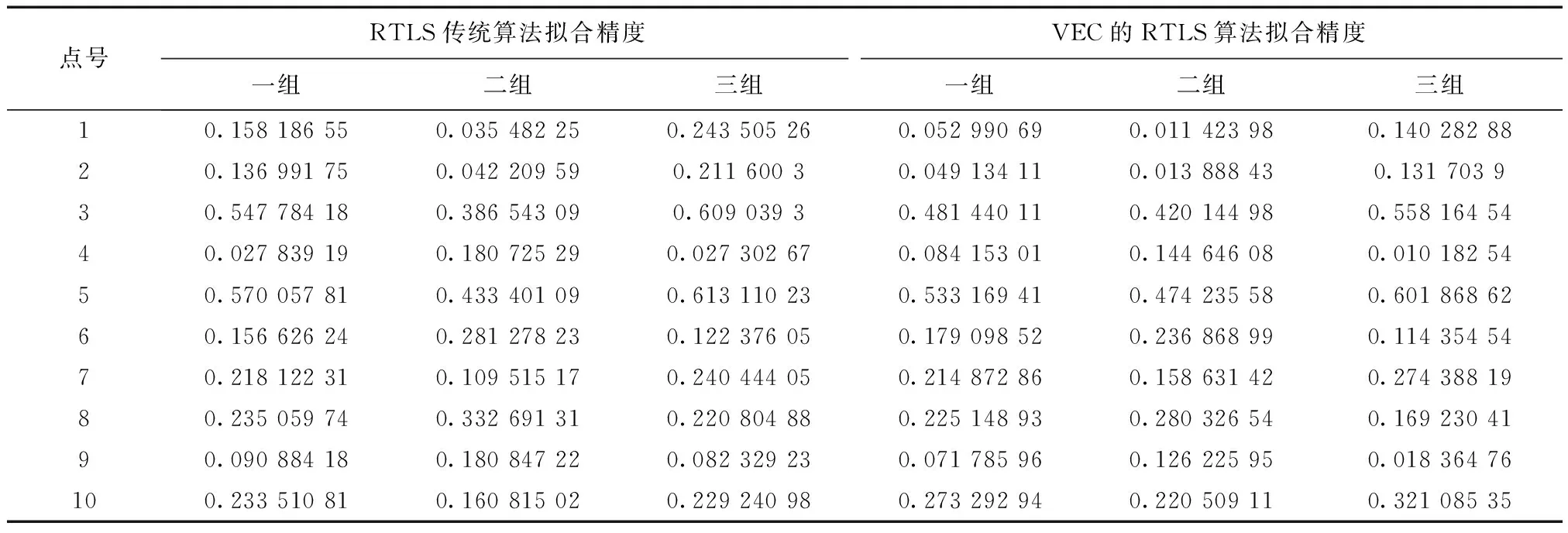
表3 不同算法拟合的模型参数精度

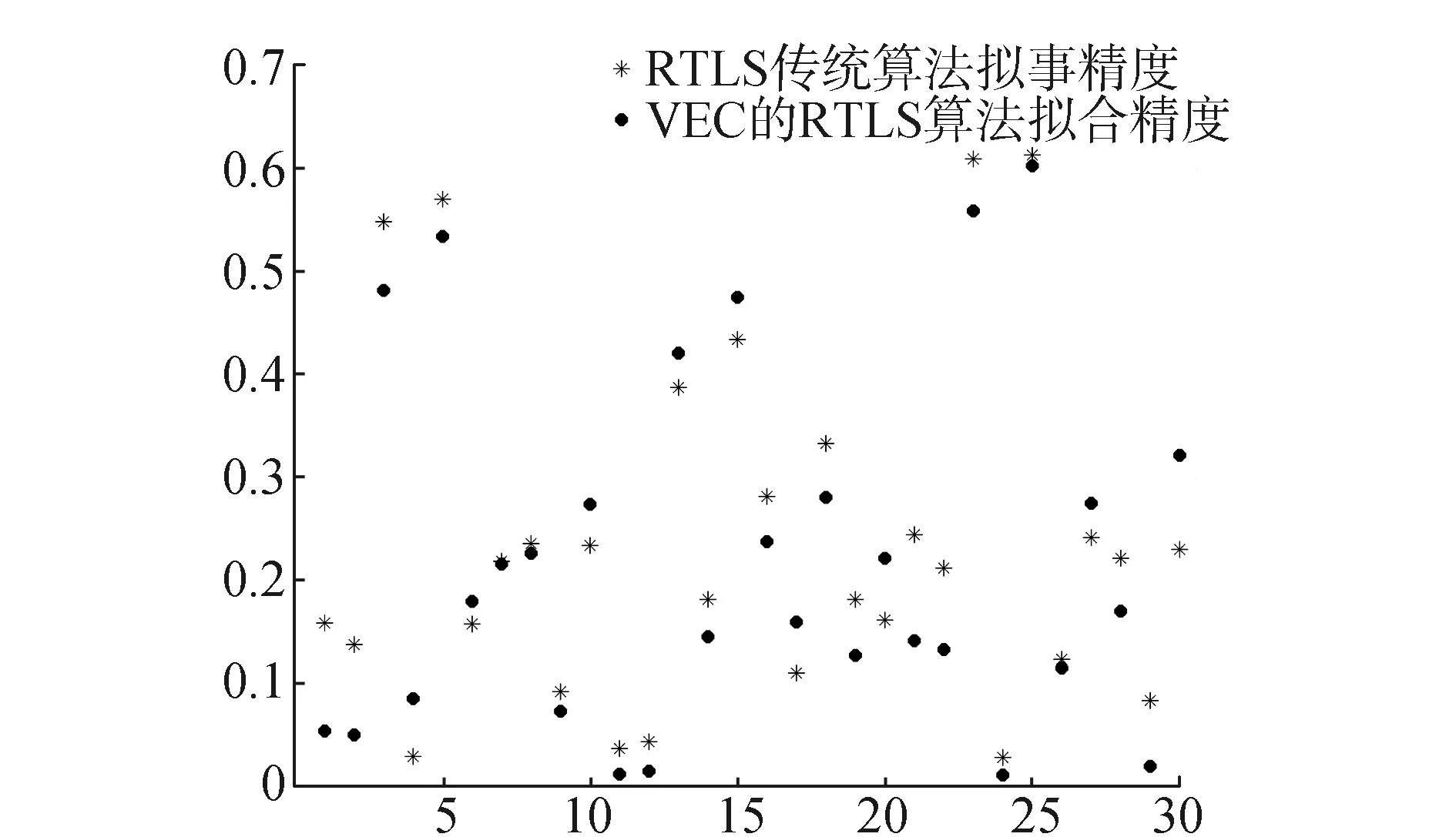
图2 两种算法拟合的误差分布

实验结果表明，应用方差分量估计建立的总体最小二乘抗差估计算法是可行的，建立算法的拟合精度优于传统总体最小二乘抗差算法。在进行的另一组模拟实验中，系数矩阵与观测向量中的元素精度存在较大差异，模拟的随机模型存在偏差，获得模型参数的精度更加显著。

4 结 论

通过对现有总体最小二乘抗差估计研究成果的分析，归纳现有算法中存在的不足。总体最小二乘抗差估计的研究思路趋同于传统算法，无法顾及EIV模型存在的系数矩阵与观测向量中的元素不属于同一精度量级引起的抗差估计问题，同时没有顾及随机模型误差对基于权函数的TLS抗差估计算法影响的问题。应用最小二乘方差分量估计建立总体最小二乘抗差估计算法，修正随机模型误差对抗差估计的影响，建立的迭代算法能够实现对系数矩阵与观测向量中的元素进行分类定权，提高应用权函数进行抗差估计的有效性。

[1] PEARSON K. On Lines and Planes of Closest Fit to Systems of Points in Space[J]. Phil Mag, 1901,2:559-572.

[2] SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-squares Approach to Empirical Coord-inate Transformations: Three Algorithms [J]. Journal of Geodesy, 2008,82(6):373-383.

[3] SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7):415-421.

[4] NEITZEL F. Generalization of total least-squares on example of unweighted and weighted 2D similarity transformation[J]. Journal of Geodesy, 2010, 84(12):751-762.

[5] MAHBOUB V. On Weighted Total Least-squares for Geodetic Transformation[J]. Journal of Geodesy, 2012,86(5): 359-367.

[6] TONG Xiaohua, JIN Yanmin, LI Lingyun. An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation [J]. Journal of Surveying Engineering, 2011, 137(4):120-128.

[7] SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011, 85(4):229-238.

[8] 方兴，曾文宪，刘经南，等. 三维坐标转换的通用整体最小二乘算法[J].测绘学报，2014， 43(11)：1139-1143.

[9] XING Fang. Weighted total least-squares with constraints: a universal formula for geodetic symmetrical transformations[J]. Journal of Geodesy, 2015, 89(5): 459-469.

[10] TAO Y Q, GAO J X, YAO Y F. TLS algorithm for GPS height fitting based on robust estimation[J]. Survey Review, 2014,46(336):184-188.

[11] 王乐洋，许才军，鲁铁定.边长变化反演应变参数的总体最小二乘方法[J].武汉大学学报(信息科学报)，2010，35(2)：181-184．

[12] SCHAFFRIN B, UZUN S. Errors-in-variables for mobile mapping algorithms in the presence of outliers[J]. Archives of Photogrammetry, 2011, 22: 377-387.

[13] 陈义，陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报，2012，41(5)：715-722．

[14] MAHBOUB V, AMIRI-SIMKOOEI A R, SHARIFI M A. Iteratively reweighted total least squares: a robust estimation in error-in-variables models[J]. Survey review, 2013, 45(329): 92-99

[15] 龚循强，李志林. 稳健加权总体最小二乘法[J]. 测绘学报，2014，43(9)：888-894.

[16] 龚循强，李志林.一种利用IGGⅡ方案的稳健混合总体最小二乘方法[J].武汉大学学报(信息科学报)，2014，39(4)：462-466．

[17] LU J, CHEN Y, LI B F,et al. Robust total least squares with reweighting iteration for three-dimensional similarity transformation[J]. Survey Review, 2014, 46(334): 28-36.

[18] 王彬，李建成，高井祥，等.抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报，2015，44(6)：602-608.

[19] WANG Bin, LI Jiancheng, LIU Chao. A robust weighted total least squares algorithm and its geodetic applications[J]. Stud. Geophys. Geod., 2016, 60: 177-194.

[20] 赵俊，归庆明. 部分变量误差模型的整体抗差最小二乘估计[J]. 测绘学报，2016，45(5)：552-559.

[21] 陶叶青，高井祥，姚一飞．基于中位数法的抗差总体最小二乘估计[J]．测绘学报，2015，45(3)：297-301．

[22] TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares variance component estimation[J]. Journal of Geodesy, 2008, 82(2): 65-82.

[23] AMIRI-SIMKOOEI A R. Application of least squares variance component estimation to errors-in-variables models[J]. Journal of Geodesy, 2013, 87(10): 935-944.

[24] XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models: algorithm and statistical analysis[J]. Journal of geodesy, 2012, 86(8): 661-675.

[25] YANG Y. Robust Estimation of Geodetic Datum Transformation[J]. Journal of geodesy, 1999, 73: 268-274.

[26] 王乐洋，许才军.附有相对权比的总体最小二乘平差[J].武汉大学学报(信息科学报)，2011，36(8)：887-890．

[27] NERI F, SAITTA G, CHIOFALO S. An accurate and straightforward approach to line regression analysis of error-affected experimental data[J]. Journal of physics E scientific instruments, 1989, 8(22): 636-638.