深部煤层底板破坏深度多元非线性预测模型

张风达

(煤炭科学研究总院，北京 100013)

随着浅部资源的日趋枯竭，煤炭资源的开采深度不断增加。尤其是华北地区的部分煤矿开采深度已达千米。华北地区深部煤层开采多面临着承压水的威胁。为预防深部煤层底板突水危险性，煤层底板破坏深度的预测是重点研究对象。国内学者从理论分析、室内试验、数值模拟和现场实测等角度对煤层底板破坏深度展开大量研究。鲁海峰等[1]运用半无限体理论计算横观各向的煤层底板应力变化规律；孟祥瑞等[2]基于半无限体理论构建了煤层底板应力模型，求解了煤层底板破坏深度；张金才[3]等运用滑移现场理论计算了煤层底板破坏深度，在此基础上，张风达等[4]对煤壁附近的塑性区范围进行了改进，并给出了相应的煤层底板破坏深度计算公式；姜耀东等[5-6]运用相似模拟研究了煤层底板破坏深度；段宏飞[7]运用数值模拟分析了煤层底板破坏深度的相关影响因素，并回归了煤层底板破坏深度六因素线性模型；孙建[8]运用数值模拟研究了煤层底板破坏深度与工作面斜长、煤层倾角的相关性；朱术云等[9]通过现场实测对煤层底板破坏深度展开研究。理论分析、室内试验、数值模拟和现场实测主要对矿井的某个工作面或者区域进行分析，存在一定的局限性。因此，部分专家学者通过统计大量的煤层底板破坏深度实测数据，分析煤层底板破坏规律及其影响因素。目前《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》(下文简称“三下”规程)[10]中给出了考虑埋深、工作面斜长、煤层倾角3个因素的煤层底板破坏深度线性回归公式；许延春等[11]考虑了煤层采厚，线性回归出400m以深的煤层底板破坏深度统计公式；李江华[12]等通过统计分析得出增加采高对煤层底板破坏深度的影响，有助于提高预测精度；程爱平[13]等运用未确知聚类优化法，选取采深、煤层倾角、采厚、构造影响程度4个主要影响因素作为判别指标，建立煤层底板采动破坏深度动态预测模型；朱志洁[14]等基于人工蜂群优化支持向量机的算法预测了深部煤层底板破坏深度。随着开采深度的不断增加，煤层底板破坏机理日趋复杂。深部煤层底板破坏深度不再由某一单个因素或几个因素决定，而呈现多因素耦合的特点。因此，现有的煤层底板破坏深度预测模型多为线性预测模型，在确定深部煤层底板破坏深度时存在一定的偏差，或基于神经网络等方法进行预测，未能给出较为简单、且易于推广的预测公式。笔者结合文献[15]搜集的17组华北型深部煤层底板破坏深度实测数据，运用非线性回归的方法、构建了多因素耦合的非线性数学模型，对比分析了“三下”规程线性回归公式，最后通过现场实例验证了非线性回归数学模型的合理性。

1 煤层底板破坏深度主控因素

煤炭资源开采使得上覆岩层压力不能通过煤层有效地传递至煤层底板，而通过采场四周的煤体传递至底板岩体，并形成一定范围的应力集中区域。当应力集中程度达到煤层底板自身承载能力时，煤层底板发生塑性变形破坏。因此煤层底板破坏主要由采动围岩应力和煤层底板岩体抗破坏能力决定。采动围岩应力大小主要受埋深、煤层倾角、采厚、工作面斜长和地质构造的影响。煤层底板岩体抗破坏能力主要受煤层底板黏聚力、内摩擦角及其完整性决定[16-17]。现有的煤层底板破坏深度预测公式和预测煤层底板破坏深度的基本参数，多未考虑底板岩性因素。考虑到统计的17组煤层底板破坏深度实测数据为华北型煤层底板，岩性相对接近，因此，主要从采动围岩应力大小的角度出发，重点分析埋深、煤层倾角、采厚、工作面斜长和地质构造5个主控因素对煤层底板破坏深度的影响。

2 建立数学模型

2.1 基础数据

文献[15]统计了74组华北型煤层底板破坏深度实测数据，从聚类分析的角度，构建了划分深浅部煤层底板破坏规律的数学模型，分析得出埋深520m为深浅部煤层底板破坏规律的分界点。由于篇幅限制，在此不做过多叙述。结合文献[15]，确定了17组华北型深部煤层底板破坏深度统计数据，具体见表1。其中，尽管潘三煤矿、新集二矿和钱营孜煤矿位于两淮矿区，但依据煤田赋存地质情况，均属于华北型煤田[18-19]。

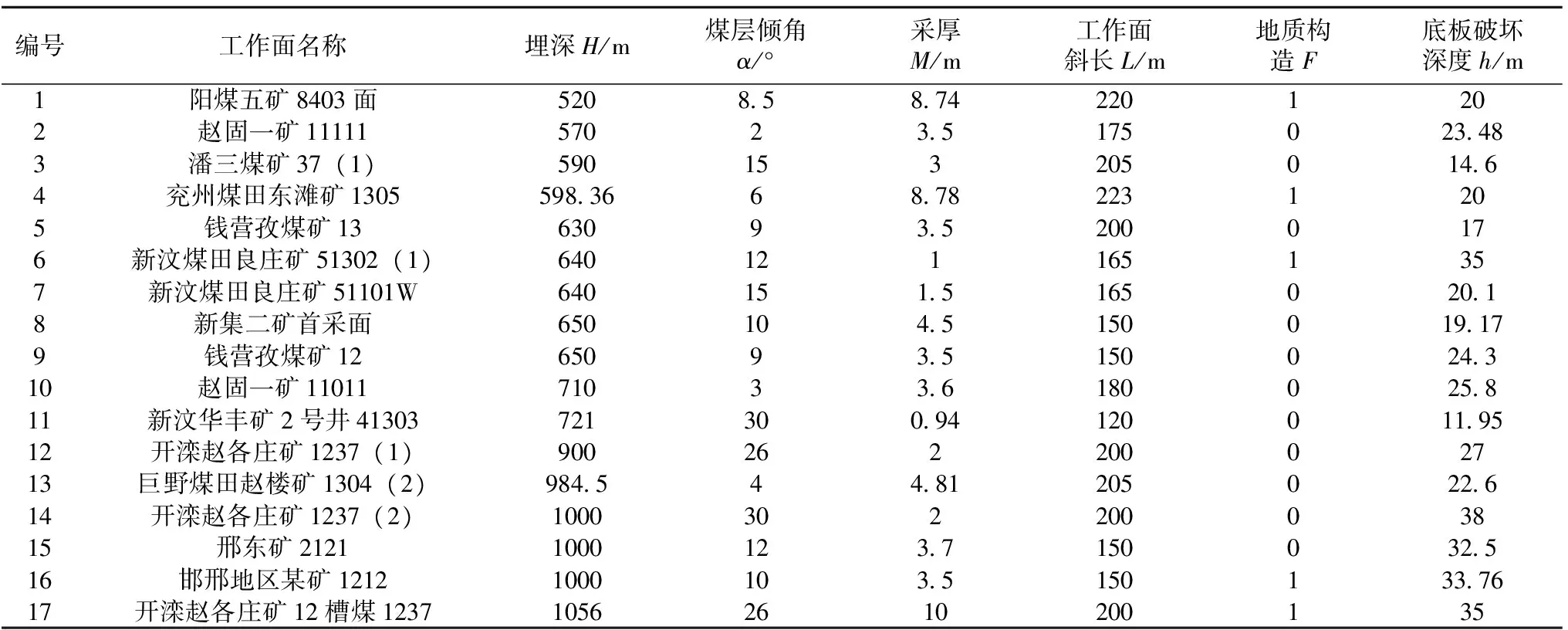
表1 华北地区石炭二叠系深部煤层底板采动破坏深度实测数据

注：地质构造F主要指断层，0表示无断层，1表示有断层。

2.2 建立数学模型

深部煤层底板处于高地应力、高地温、高渗透水压力的状态下，其变形破坏呈现非线性、多因素耦合的特点[20]。而“三下”规程中给出的煤层底板破坏深度预测公式仅与埋深、煤层倾角和工作面斜长3个因素呈线性相关，具体见式(1)。

h=0.0085H+0.1665α+0.1079L-4.3579

(1)

式中，h为煤层底板破坏深度，m；H为埋深，m；α为煤层倾角，(°)；L为工作面斜长，m。

式(1)难以诠释深部煤层底板破坏非线性的特点，因此运用多元非线性回归的方法构建深部煤层底板破坏深度数学模型更为合理。考虑到地质构造F为0或1，未能充分体现非线性影响。因此，在考虑埋深H、煤层倾角α、工作面斜长L和采厚M非线性影响的基础上，构建了多个因素耦合的分量。主要分为煤层底板应力分布和煤层底板采动范围影响两部分。在煤层底板应力分布方面，深部煤层开采过程中，应力变化幅度对煤层底板破坏特征的影响较为明显，因此，考虑了埋深与煤层倾角两因素的耦合作用，将埋深H与煤层倾角α正弦值的乘积命名为上覆岩层自重沿岩层倾向的切向分量N。在采动范围影响方面，将工作面斜长L与采厚M的乘积命名为采动空间S；将采厚M与煤层倾角α正弦值的乘积命名为煤壁分布特征W；根据参考文献[10]规定的覆岩破坏高度预测公式，以煤层厚度的非线性参量修正深部煤层开采的覆岩破坏对煤层底板破坏深度的影响，给出煤层厚度的计算公式；参考文献[11]，煤层厚度是煤层底板破坏深度的重要因素，因此，重点考虑了采厚与工作面斜长、煤层倾角的耦合关系影响。基函数见式(2)。

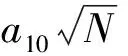
(2)

通过多元非线性回归分析，得出深部煤层底板破坏深度数学模型，具体见式(3)。

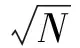
(3)

从式(3)可知，深部煤层底板的原岩应力较大，采动后底板应力变化幅度随之增加，煤层底板破坏深度呈增大的变化特点。煤层倾角与煤层底板破坏深度关系较为复杂，以煤层倾角的正弦函数和余弦函数的形式，分析其对煤层底板破坏深度的影响。煤层倾角在一定程度上影响了上覆岩层的传递至煤层底板的切向应力，由于煤层倾角(2～30°)引起上覆岩层应力分布至采掘空间周边煤岩体的应力分量增加，而作用于煤层底板的应力垂直分量减小，导致采动后煤层底板的卸荷程度减小，从而减小了煤层底板破坏深度。随着工作面斜长的增加，煤层底板采动卸荷范围和卸荷程度增大，煤层底板破坏深度增大。煤层厚度对煤层底板破坏深度的作用机理较为复杂，煤层厚度增加，在工作面斜长一定的情况下，增大了采动影响范围，加剧了煤层底板的卸荷程度；但是煤层厚度的增加，在一定程度上弱化了上覆岩层传递至煤层底板的应力集中程度，尤其是松软煤层，将对上覆岩层的集中应力呈“褥垫效应”[9]；此外，倾斜煤层的煤壁塑性区破坏情况还受煤层倾角和煤层厚度的耦合影响。地质构造在一定程度上增大了煤层底板破坏深度。分析得出多元非线性耦合回归结果与实测结果的相关系数为0.9474(相关系数大于0.85)，说明拟合程度高。

3 误差分析

为明确多元非线性回归公式的准确性，对比分析多元非线性回归的计算公式(3)与“三下”规程中给出的煤层底板破坏深度计算公式(1)，具体结果见表2。

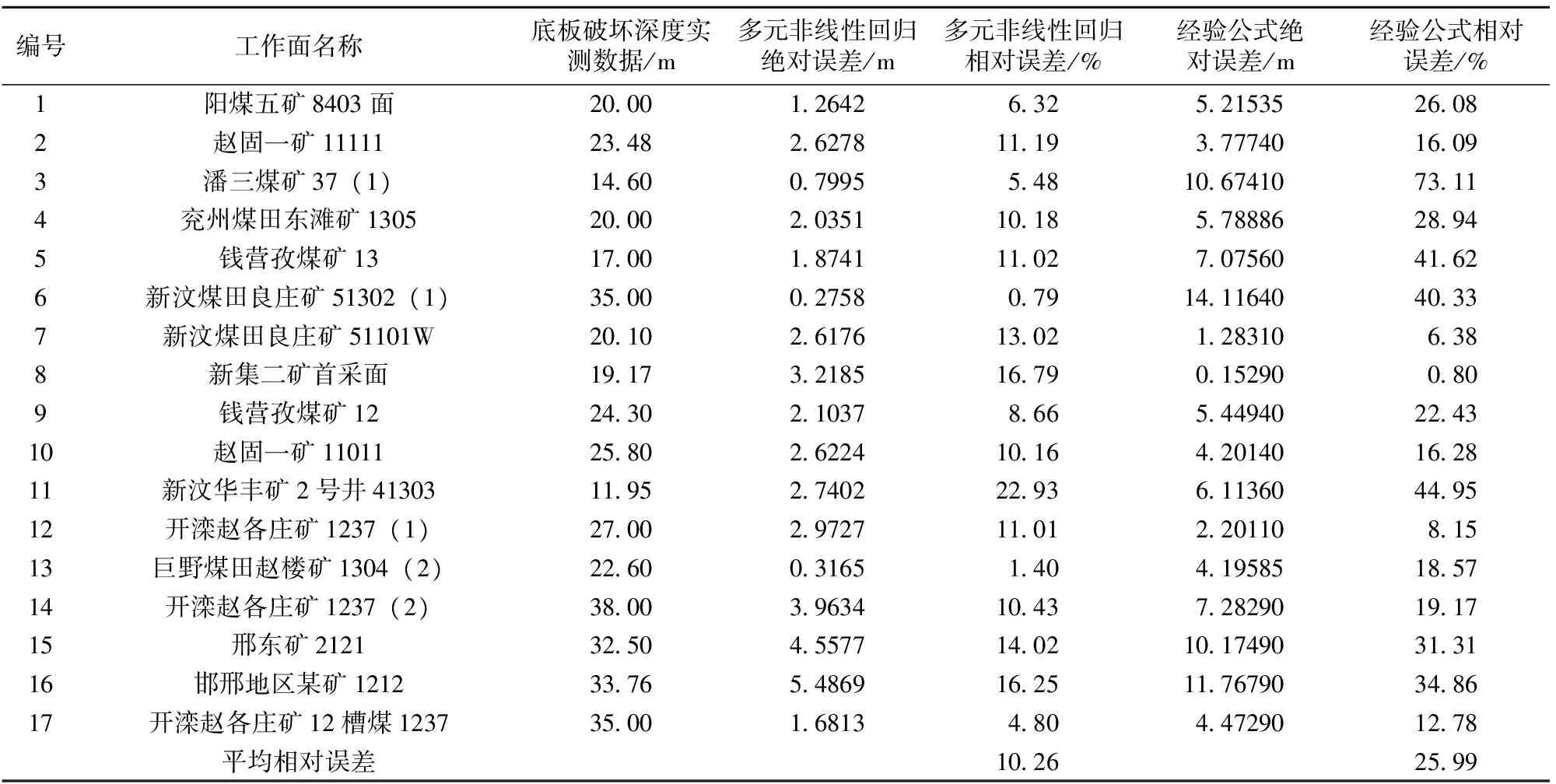
表2 深部煤层底板多元非线性回归数据、“三下”规程回归数据与实测数据的误差分析

从表2可以看出，多元非线性回归公式的相对误差的平均值为10.26%，远小于经验公式相对误差的平均值25.99%，说明深部煤层底板破坏呈多因素耦合、非线性变化特点。

4 现场实例

峰峰矿区某矿深部112145工作面平均埋深为636m，平均斜长为170m，煤层平均厚度4.2m，煤层平均倾角20°，煤层结构简单、无地质构造。通过钻孔应力计和注水试验法现场实测得出煤层底板破坏深度介于18.19～20.24m之间。为验证深部煤层底板破坏深度数学模型的合理性，对比分析式(1)与式(3)计算得出112145工作面煤层底板破坏深度，具体如表3。

表3 煤层底板破坏深度回归公式预测对比

由表3分析可知，多元非线性回归数学模型预测的深部煤层底板破坏深度与实际情况相吻合，而“三下”规程线性回归预测得出的煤层底板破坏深度误差相对较大。说明深部煤层底板破坏深度采用多元非线性回归数学模型进行预测更为合理，为预测华北型深部煤层底板破坏深度提供参考。

5 结 论

(1)结合17组华北型深部煤层底板破坏深度实测数据，运用多元非线性回归方法拟合出深部煤层底板破坏深度数学模型。

(2)结合17组华北深部煤层底板破坏深度实测数据，分别运用深部煤层底板破坏深度数学模型、“三下”规程给出的计算公式进行预测，并与实测数据进行差值分析，分析得出多元非线性回归公式相对误差的平均值为10.26%，远小于经验公式相对误差的平均值25.99%，说明深部煤层底板破坏具有多因素耦合、非线性变化的特点。

(3)结合峰峰矿区某矿深部112145工作面的实际参数，对比分析得出深部多元非线性回归数学模型的结果与实际情况基本吻合，且预测精度高于“三下”规程给出的计算公式，说明该数学预测模型更为合理。

[1]鲁海峰，姚多喜，梁修雨，等.采动底板横观各向同性岩体应力解析解[J].地下空间与工程学报，2013，9(5):1050-1056.

[2]孟祥瑞，徐铖辉，高召宁，等.采场底板应力分布及破坏机理[J].煤炭学报，2010，35(11):1832-1836.

[3]张金才，刘天泉.论煤层底板采动裂隙带的深度及分布特征[J]煤炭学报，1990，15(2):46-54.

[4]张风达，高召宁，孟祥瑞.采场底板塑性区分布及破坏机理研究[J].长江科学院院报，2012， 29(11): 59-61.

[5]姜耀东，吕玉凯，赵毅鑫，等.承压水上开采工作面底板破坏规律相似模拟试验[J].岩石力学与工程学报，2011，30(8):1571-1578.

[6]赵毅鑫，姜耀东，吕玉凯，等.承压工作面底板破断规律双向加载相似模拟试验[J].煤炭学报，2013，38(3):384-390.

[7]段宏飞.煤矿底板采动变形及带压开采突水评判方法研究[D].徐州:中国矿业大学，2012.

[8]孙 建.沿煤层倾斜方向底板“三区”破坏特征分析[J].采矿与安全工程学报，2014，31(1):115-121.

[9]朱术云，曹丁涛，周海洋，等.采动底板岩性及组合结构对破坏深度的制约作用[J].采矿与安全工程学报，2014，31(1):90-96.

[10]国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社，2008.

[11]许延春，杨 扬.大埋深煤层底板破坏深度统计公式及适用性分析[J].煤炭科学技术，2013，14(9):129-132.

[12]李江华，许延春，谢小锋，等.采高对煤层底板破坏深度的影响[J].煤炭学报，2015，40(S2):303-310.

[13]程爱平，高永涛，梁兴旺，等.基于未确知聚类法的底板采动破坏深度动态预测[J].采矿与安全工程学报，2014，31(5):739-744.

[14]朱志洁，张宏伟，王春明.基于人工蜂群算法优化支持向量机的采场底板破坏深度预测[J].重庆大学学报，2015，38(6):37-43.

[15]张风达.深部煤层底板变形破坏机理及突水评价方法研究[D].北京：中国矿业大学(北京)，2016.

[16]刘伟韬，刘士亮，姬保静.基于正交试验的底板破坏深度主控因素敏感性分析[J].煤炭学报，2015，40(9):1995-2001.

[17]段宏飞.底板破坏深度六因素线性预测模型[J].岩土力学，2014，35(11):3323-3330.

[18]李增学，魏久传，金秀昆.淮南煤田二叠系高分辨率层序地层学特征[J].地层学杂志，2000，24(1):34-39.

[19]陈陆望，许冬清，殷晓曦，等.华北隐伏型煤矿区地下水化学及其控制因素分析———以宿县矿区主要突水含水层为例[J].煤炭学报，2017，42(4):996-1004.

[20]何满潮，钱七虎，等.深部岩体力学基础[M].北京:科学出版社，2010.

[21]施龙青，徐东晶，邱 梅，等.采场底板破坏深度计算公式的改进[J].煤炭学报，2013，38(S2)：299-303.

[22]张文泉，赵 凯，张贵彬，等.基于灰色关联度分析理论的底板破坏深度预测[J].煤炭学报，2015，40(S1)：53-59.