基于先验信息稀疏恢复的非均匀样本检测方法

李志汇， 张永顺,2， 刘汉伟， 王强， 刘洋

(1.空军工程大学 防空反导学院, 陕西 西安 710051; 2.信息感知技术协同创新中心, 陕西 西安 710077)

0 引言

机载雷达的主要应用就是对地面、海面弱小运动目标进行检测，但是严重的地海杂波将导致待检测的微弱目标淹没在杂波背景中，严重影响了运动目标的检测性能。而空时自适应处理(STAP)技术对空时二维回波数据进行联合处理，能够有效地将杂波和目标在空时二维域中分离出来[1-2]。为了精确地估计杂波协方差矩阵，通常需要足够多独立同分布(IID)的训练样本来估计杂波协方差矩阵。然而，杂波环境并不是理想的，而是非均匀的、非平稳的，尤其是当训练样本被干扰目标(运动目标或者强散射点)污染时，将会引起杂波协方差矩阵估计不准，进而导致目标信号自相抵消[3]。为了解决样本非均匀导致STAP目标检测性能下降的问题，必须要剔除被干扰目标污染的训练样本。广义内积(GIP)方法[4-5]作为一种典型的非均匀检测器(NHD)，可以用来剔除非均匀环境中被污染的训练样本，但是当训练样本中包含的被污染样本数比较多时，GIP方法不能有效地检测包含干扰目标的非均匀样本。其主要原因是由于GIP方法所采用的杂波协方差矩阵不精确，针对这一问题，一些学者利用系统参数等先验信息直接估计杂波协方差矩阵[6]，一些学者利用系统参数等知识计算扁长椭球函数来估计杂波协方差矩阵[7-9]，然后与GIP方法结合来剔除被污染的样本；另外一种思路则是直接对训练样本进行处理来寻找训练样本集中的奇异点，如K均值聚类算法[10]、S变换法[11]、矩阵相似度法[12]。为了保证所选择的训练样本与待检测单元具有相似的杂波统计特性，文献[13]和文献[14]分别提出了子孔径平滑技术和谱相似技术来估计训练样本的杂波协方差矩阵与待检测单元杂波协方差矩阵的相似性。为了提高知识辅助样本选择方法的稳健性，文献[15]提出了一种基于子空间的阵元误差估计方法。近年来，基于稀疏恢复(SR)[16]的STAP方法开辟了一种新的思路，文献[17]提出了一种基于稀疏重构的训练样本选择方法，文献[18]提出了一种基于联合稀疏功率谱恢复的方法来抑制离群点。

本文针对非均匀样本(样本中包含干扰目标)检测问题提出一种基于先验信息SR的非均匀样本检测方法，首先从理论上对GIP方法存在的问题进行了分析，并提出采用欠定系统局灶解法(FOCUSS)恢复待检测单元的稀疏表示系数，并给出了“稀疏滤波器”的设计方法，用其滤除待检测单元中的目标信号和“伪点”的影响，最后与GIP方法结合进行非均匀样本检测。仿真结果表明，所提的方法能够有效地检测出被干扰目标污染的训练样本，提升了STAP在非均匀环境下的目标检测性能。

1 信号模型

以机载正侧视均匀线阵相控阵雷达系统为例进行分析。如图1所示，载机沿着X轴正方向飞行，高度为H，速度为v，雷达工作波长为λ，天线阵列由N个阵元组成，阵元间距为d，并设d=λ/2，距离环内杂波散射块到载机的距离为Rl，相对于载机的方位角、俯仰角和空间锥角分别为θ、φ和ψ.

每个阵元在相干处理间隔(CPI)内发射和接收K个脉冲，则N个阵元在第l个距离单元接收到的K个脉冲回波数据[1]可以表示为

(1)

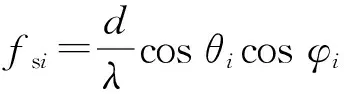
信号和杂波的空时导向矢量可以统一表示为

vi(fsi,fdi)=b(fsi)⊗a(fdi),

(2)

式中：⊗表示Kronecker积；b(fsi)和a(fdi)分别为空域导向矢量和时域导向矢量，可以表示为

b(fsi)=[1,ej2πfsi,…,ej2π(N-1)fsi]T,

(3)

a(fdi)=[1,ej2πfdi,…,ej2π(K-1)fdi]T,

(4)

其中(·)T表示矩阵转置操作。

根据STAP基本原理可以得到最优STAP权矢量为

(5)

式中：(·)H表示共轭转置操作；R∈CNK×NK为真实的杂波协方差矩阵，实际情况下R是未知的，一般通过待检测单元邻近的L个IID的训练样本估计得到样本协方差矩阵，即

(6)

2 基于先验信息稀疏恢复的非均匀样本检测方法

2.1 传统GIP方法及存在的问题

GIP算法是一种典型的NHD，当获得精确的杂波协方差矩阵时能够有效检测被污染的训练样本， GIP的检验统计量为

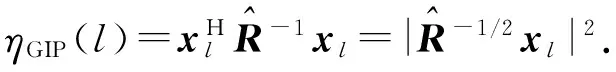
(7)

含有干扰目标的训练样本可以表示为

xl=xJ+cl+nl,

(8)

式中：xJ=αJvJ(fsJ,fdJ)为存在于训练样本中的干扰目标信号，其中αJ和vJ(fsJ,fdJ)分别为干扰目标的幅值和导向矢量，fsJ和fdJ分别为干扰目标的归一化空域频率和多普勒频率。

将(8)式代入(6)式可以将样本协方差矩阵分解为两部分：

=cl+nl+Δ,

(9)

(10)

(11)

对(9)式分析可知：当均匀训练样本充足、被干扰目标污染的训练样本比较少时(L0较小)，Δ比较小，从而≈cl+nl，采用设计的检验统计量能够将被干扰目标污染的训练样本识别出来；但是，当均匀训练样本比较少，而且被干扰目标污染的训练样本占总的训练样本的比例比较大时(L0较大)，Δ比较大，与cl+nl差别比较大，采用设计的检验统计量不能将被干扰目标污染的训练样本识别出来。另外，如果没有包含待检测单元的杂波信息，则GIP方法挑选出的训练样本估计的杂波协方差矩阵与待检测单元的杂波协方差矩阵不具有统计意义上的相似性。

2.2 基于先验信息SR的非均匀样本检测方法

2.2.1 待检测单元稀疏表示系数的计算

首先将角度- 多普勒平面离散化得到NsNd个网格点，其中Ns=ρsN，Nd=ρdK，ρs和ρd均表示分辨尺度，则(1)式的回波数据可以表示为

(12)

式中：Φ=[v1,v2,…,vNsNd]表示空时导向矢量构成的超完备字典；α=[α1,α2,…,αNsNd]T表示稀疏表示系数，其反映了xl在Φ上的分布，也称为杂波空时谱[15]，通常情况下α是稀疏的(只有少量的非零元素)。可以通过最小化L1范数近似求解(12)式中的欠定问题，

=arg min ‖α‖1， s.t.‖xl-Φα‖≤ε,

(13)

式中：ε为噪声允许误差。考虑到FOCUSS算法[19]的计算复杂度低、SR性能较好，本文采用FOCUSS算法求解(13)式。

采用FOCUSS算法对待检测单元的数据进行SR处理，得到待检测单元的稀疏表示系数α0. 然而，待检测单元的数据中包含目标信号，所以恢复得到的α0中也包含目标信息；另一方面，仅用待检测单元的单帧数据恢复出的α0中包含少量“伪点”，这对后续污染样本的剔除将产生严重影响。针对上述问题，下面利用机载雷达系统参数的先验信息设计“稀疏滤波器”对α0进行处理，滤除其中包含的目标和“伪点”等信息。

2.2.2 基于先验知识的“稀疏滤波器”设计

在正侧视几何结构下，杂波能量(或者称为杂波脊)理论上在角度- 多普勒面内呈直线刀背式分布，斜率为γ=fdi/fsi=2v/dfr，而目标在角度多普勒平面内与杂波脊是相互分离的。基于此，可以对待检测单元的数据通过SR得到包含杂波和目标的空时谱，然后根据杂波和目标在角度- 多普勒域相互分离的特性设计“稀疏滤波器”滤除目标。具体步骤如下：

步骤1根据雷达系统的平台运动速度、工作波长、脉冲重复频率等先验信息计算得到杂波脊的斜率γ，假定正侧视阵下γ=1.

步骤2根据得到的杂波脊先验信息，在离散化角度- 多普勒平面的杂波脊附近选取若干网格点确定“稀疏滤波器”的权值。

“稀疏滤波器”定义为T=[t1,t2,…,tNsNd]T，其中每个元素ti表示离散化角度- 多普勒平面中的一个网格点，并且ti={0,1}. 当该网格点位于杂波脊附近的区域Ω时，ti=1，否则ti=0.Ω的判定方法为Ω={(fsi,fdi)||fsi-fdi|γ≤δ}，其中δ表示容许限度，用以说明在杂波脊附近选择区域的大小。

步骤3采用“稀疏滤波器”滤除目标，得到待检测单元滤除目标后的杂波空时谱为

0=T⊙α0,

(14)

式中：⊙表示Hadamard积。

利用(14)式滤波目标的同时也能滤波SR估计空时谱时出现的“伪点”。

(15)

式中：β表示对角线量。

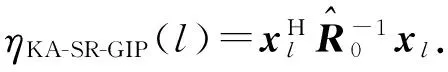
(16)

(16)式得到的先验信息SR非均匀样本检测检验统计量仅包含待检测单元的杂波统计特性，利用其挑选的训练样本计算得到的杂波协方差矩阵在统计意义上与待检测单元相似。

2.2.3 基于KA-SR-GIP方法

基于KA-SR-GIP检测方法的具体步骤如下：

步骤1采用FOCUSS算法对待检测单元的训练样本进行稀疏表示，得到待检测单元的稀疏表示系数α0.

步骤2根据雷达系统参数计算得到杂波脊的先验信息γ，然后设计“稀疏滤波器”T，并采用(14)式对α0进行处理，滤除α0中含有的目标和“伪点”信息，然后依据(15)式计算得到待检测单元的杂波协方差矩阵0.

步骤3根据(16)式计算得到基于KA-SR-GIP检验统计量ηKA-SR-GIP，并根据新的检验统计量ηKA-SR-GIP检测和剔除非均匀样本。

步骤4估计杂波协方差矩阵，主要采用更新后的均匀训练样本，然后进行STAP处理。

3 仿真结果与分析

采用MATLAB R2013a软件进行仿真，机载相控阵雷达仿真参数设置如下：载机高度8 000 m，速度140 m/s，工作波长0.23 m，阵元个数10个，脉冲个数10个，阵元间距0.115 m，脉冲重复频率2 434.8 Hz. 雷达波束指向目标方向，即目标的归一化空域频率为0，归一化多普勒频率为-0.25. 选取203个训练样本，对应203个距离门，杂噪比(CNR)为50 dB，目标位于待检测单元中，对应第102个距离门，信噪比(SNR)为10 dB，第101个和第103个距离门设定为保护单元。8个干扰目标分别位于第10个、第20个、 第30个、第50个、第150个、第170个、第180个、第190个距离门中，对应的干噪比(JNR)分别为2 180个、190个距离门中，对应的JNR分别为25 dB 、20 dB 、25 dB、20 dB、20 dB、30 dB、30 dB、25 dB. 干扰目标均位于主波束内，其与目标具有相同的归一化空域频率和归一化多普勒频率。分辨尺度均为4，即ρs=ρd=4. “稀疏滤波器”的容许限度δ=0.1，根据空时网格点是否在Ω中来选择杂波脊附近区域，红色区域为空时网格点在Ω中的杂波脊附近区域，反之为蓝色区域，具体如图2所示。

3.1 被污染样本的检测性能

图3和图4给出了GIP方法和KA-SR-GIP方法对被污染样本的检测性能。仿真过程中，剔除待检测单元和保护单元的样本，只对剩余的训练样本进行处理。从图3可以看出，GIP方法只能检测出位于第10个、第30个、第170个、第180个距离门中的被污染样本，而不能检测出位于第20个、第50个、第150个、第190个距离门中的被较弱强度干扰污染的训练样本。这是因为GIP方法采用的估计样本协方差矩阵不准确。与图4进行对比可知，KA-SR-GIP方法能够有效地检测出被不同强度干扰污染的训练样本。

3.2 目标检测性能对比

图5给出了GIP方法和KA-SR-GIP方法在剔除被污染样本后进行STAP处理的输出功率。从图5中可以看出：KA-SR-GIP方法在第102个距离门处形成了明显的目标尖峰[20]，即该距离门处的输出功率高于其他距离门中最高的输出功率约17 dB，能够将目标有效地检测出来；而GIP方法由于没有将被污染的样本剔除干净，导致待检测单元的目标被干扰目标相消，也就是在第102个距离门处没有形成尖峰。

图6给出了GIP方法和KA-SR-GIP方法在剔除被污染样本后进行STAP处理的改善因子(IF)。从图6可以看出：GIP方法中目标在干扰目标所在的归一化多普勒频率为-0.25附近会产生一个大约15 dB的凹陷，即目标在该处附近会造成目标信号被干扰目标相消，这是因为GIP方法没有将被干扰目标污染的训练样本剔除干净；而本文的KA-SR-GIP方法则由于剔除了所有被污染的训练样本，所以在归一化多普勒频率为-0.25附近没有产生凹陷，从而避免目标信号的相消现象。

图7给出了GIP方法和KA-SR-GIP方法的目标检测概率随输入SNR变化曲线。仿真过程中，仿真模型采用Swerling I型目标检测[21]，虚警概率为10-6，每个输入SNR进行200次蒙特卡洛仿真。从图7中可以看出，当输入SNR在-20 dB到28 dB之间时，同一SNR输入下，KA-SR-GIP方法比GIP方法的检测概率高，这是因为GIP方法没有将被干扰目标污染的训练样本剔除干净，导致样本中含有的干扰目标影响了对目标的检测。

综上所述，由于训练样本被干扰目标所污染使得样本协方差矩阵估计与真实杂波协方差矩阵存在较大的偏差，从而使GIP检验统计量不能有效地剔除干扰目标，那么干扰目标将会对消待检测的目标，导致GIP方法的目标检测性能下降。而本文使用的KA-SR-GIP方法利用先验知识并采用SR方法直接估计待检测单元的杂波协方差矩阵，没有受到干扰目标的影响，所以能够有效地检测出被干扰目标污染的训练样本，不会产生目标信号相消现象，提升了目标检测性能。

4 结论

本文针对训练样本被干扰目标污染引起杂波协方差矩阵估计不准、导致目标信号自相消的问题，提出了一种基于先验信息SR的非均匀样本检测方法。该方法利用待检测单元的数据和系统参数等先验知识来估计待检测单元的协方差矩阵，并与GIP方法结合得到检验统计量ηKA-SR-GIP，来检测被干扰目标污染的非均匀样本。相比传统GIP方法，本文方法无需训练样本来估计杂波协方差矩阵，故不受干扰目标的影响，能够估计比较精确的杂波协方差矩阵。仿真结果分析表明，相比传统GIP方法，本文的方法能够有效地检测出被干扰目标污染的训练样本，提升了STAP在非均匀环境下的目标检测性能。需要指出的是，本文所提算法的前提条件是先验信息比较准确，如何在先验信息存在偏差时进行非均匀样本检测是下一步的研究重点。

)

[1] Ward J.Space-time adaptive processing for airborne radar [R]. Lexington, MA, US: MIT Lincoln Laboratory, 1994.

[2] Klemm R. Principles of sparse-time adaptive processing [M]. London, UK: Institute of Electrical Engineering, 2006.

[3] Melvin W L. Space-time adaptive radar performance in heterogeneous clutter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36 (2):621-633.

[4] Melvin W L, Wicks M C. Improving practical space-time adaptive radar [C]∥Proceedings of National Radar Conference on Aerospace and Components. Syracuse, NY, US: IEEE,1997: 48-53.

[5] Rangaswamy M. Statistical analysis of the nonhomogeneity detector for non-Gaussian interference backgrounds [J]. IEEE Transactions on Signal Processing, 2005, 53 (6): 2101-2111.

[6] 周宇，张林让，刘楠，等. 空时自适应处理中基于知识的训练样本选择策略[J]. 系统工程与电子技术, 2010, 32 (2):405-409.

ZHOU Yu, ZHANG Lin-rang, LIU Nan, et al. Knowledge aided secondary data selection in space time adaptive processing [J]. Systems Engineering and Electronics, 2010, 32 (2):405-409. (in Chinese)

[7] Yang X P, Liu Y X, Long T. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing [J]. IET Radar, Sonar and Navigation, 2013, 7 (1):47-54.

[8] 王珽，赵拥军. 知识辅助的机载MIMO雷达STAP非均匀样本检测方法[J]. 系统工程与电子技术, 2015, 37 (10):2260-2265.

WANG Ting, ZHAO Yong-jun. Knowledge-aided non-homogeneous samples detection method for airborne MIMO radar STAP [J]. Systems Engineering and Electronics, 2015, 37 (10):2260-2265. (in Chinese)

[9] Du W T, Liao G S, Yang Z W. Robust space time processing based on bi-iterative scheme of secondary data selection and PSWF method [J]. Digital Signal Processing, 2016, 52(C):64-71.

[10] Kang S, Ryu J, Lee J, et al. Analysis of space-time adaptive processing performance usingK-means clustering algorithm for normalisation method in non-homogeneity detector process [J]. IET Signal Processing, 2011, 5(2):113-120.

[11] 高志奇，陶海红，赵继超. 基于S变换的机载雷达稳健空时自适应算法[J]. 系统工程与电子技术, 2016, 38(6):1268-1275.

GAO Zhi-qi, TAO Hai-hong, ZHAO Ji-chao. Robust space-time adaptive processing based on S transform for airborne radar [J]. Systems Engineering and Electronics, 2016, 38(6):1268-1275. (in Chinese)

[12] 王强，张永顺，刘汉伟，等. 基于矩阵相似度的空时二维干扰检测方法[J]. 系统工程与电子技术, 2017, 39(2):259-262.

WANG Qiang, ZHANG Yong-shun, LIU Han-wei, et al. Interference detecting method for space-time two-dimension based on matrix similarity [J]. Systems Engineering and Electronics, 2017, 39 (2):259-262. (in Chinese)

[13] Wu Y F, Wang T, Wu J X, et al. Training sample selection for space-time adaptive processing in heterogeneous environments [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4):691-695.

[14] Wu Y F, Wang T, Wu J X, et al. Robust training samples selection algorithm based on spectral similarity for space-time adaptive processing in heterogeneous interference environments [J]. IET Radar, Sonar and Navigation, 2015, 9 (7):778-782.

[15] Sun K, Meng H, Wang Y, Wang X. Direct data domain STAP using sparse representation of clutter spectrum [J]. Signal Processing, 2011, 91 (9): 2222-2236.

[16] 姜磊，王彤. 基于子空间的阵元误差估计方法[J].系统工程与电子技术, 2014, 36(4): 656-660.

JIANG Lei, WANG Tong. Array error estimation using subspace-based approach[J]. Systems Engineering and Electronics, 2014, 36(4): 656-660. (in Chinese)

[17] 刘汉伟，张永顺，王强，等. 基于稀疏重构的机载雷达训练样本挑选方法[J]. 系统工程与电子技术, 2016,38(7):1532-1537.

LIU Han-wei, ZHANG Yong-shun, WANG Qiang, et al. Training sample selection for airborne radar algorithm based on sparse reconstruction [J]. Systems Engineering and Electronics, 2016, 38 (7):1532-1537. (in Chinese)

[18] 高志奇，陶海红，赵继超. 基于联合稀疏功率谱恢复的机载雷达稳健STAP算法研究[J]. 电子学报, 2016, 44 (11):2796-2801.

GAO Zhi-qi, TAO Hai-hong, ZHAO Ji-chao. Robust STAP algorithm based on joint sparse recovery of clutter spectrum for airborne radar [J]. Acta Electronica Sinica, 2016, 44 (11):2796-2801. (in Chinese)

[19] Gorodnitsky I F, Rao B D. Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm [J]. IEEE Transactions on Signal Processing, 1997, 45(3):600-616.

[20] 朱轶昂. 稳健功率谱稀疏恢复空时自适应处理方法研究[D]. 深圳：深圳大学, 2017.

ZHU Yi-ang. Research on robust spatial-temporal spectrum recovery for space-time adaptive processing[D]. Shenzhen:Shenzhen University, 2017.(in Chinese)

[21] Shnidman D A. Expanded swerling target models [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3):1059-1069.