超聚能射流形成过程机理研究
徐文龙, 王成, 徐斌
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
0 引言
聚能装药作为一种产生高能量密度的技术,在军事领域和民用领域得到了广泛的应用[1-2]。近年来,随着现代科技的发展,各种军事目标的防护能力不断提高,采用传统聚能装药摧毁目标越来越困难,这就对射流性能提出了更高要求[3]。传统聚能射流理论及实验研究表明,只有部分靠近药型罩内层的材料形成对穿深有贡献的射流,而大部外层材料形成对穿深基本无贡献的杵体。因此,设计一种新型聚能装药结构,使得形成射流的药型罩内层材料转化为杵体,形成杵体的药型罩外套材料形成射流,且其形成射流的速度能够达到传统射流的速度,即形成射流速度高、有效质量大的超聚能射流,对实现装甲目标的高效毁伤具有重要意义。
俄罗斯学者Minin等[4]在传统聚能装药基础上提出了超聚能装药领域,并定义了超聚能射流现象。国内对于超聚能的研究成果较少,王成等[5]于2014年率先对药型罩截顶加附加装置的超聚能装药结构进行了数值模拟研究;钱俊松[6]通过数值模拟的方法对超聚能装药结构进行了优化设计;王淦龙[7]对截顶辅助罩超聚能装药结构及喷射型超聚能装药结构进行了数值模拟研究;李庆鑫等[8]对“蘑菇形”超聚能装药结构进行了数值模拟研究。目前,国内对于超聚能射流的研究大多停留在数值模拟层面,超聚能射流的理论和作用规律方面还有待深入研究,数值研究结论没有有效的试验支撑。本文通过理论分析、数值模拟及试验验证相结合的方式给出了超聚能射流形成的理论模型,分析了超聚能射流形成过程并进行了优化设计。通过对比试验,证明了超聚能装药破甲能力远大于传统聚能装药结构,在试验工况中,超聚能射流的侵彻深度为传统聚能射流的2.3倍。
1 超聚能射流形成过程机理
1.1 传统聚能射流形成过程机理
传统聚能射流的理论属于理想不可压缩流体的射流理论。图1为压合角β(β<90°)在碰撞点观测的两股理想不可压缩流体对称碰撞的示意图。由于射流碰撞过程是对称的,只需要研究射流半平面流动情况,如图2所示。其中,u0和m分别为来流的速度和质量,uJ和mJ分别为沿OX轴正方向运动射流的速度和射流质量,uS和mS分别为沿OX轴负方向运动射流的速度和杵体质量。
由文献[9]可知:
(1)
在聚能射流形成过程中,设药型罩的压合速度为v0且方向与药型罩表面垂直,如图3所示。这时爆轰波将同时冲击药型罩与装药接触的全部表面,药型罩锥角2α=2β,速度v0可以分解为沿罩母线方向的分量u0和沿OX轴正方向的分量vK,由几何关系可知:
(2)
由(1)式和(2)式可知,沿罩母线方向的分量u0=uJ=uS=v0/tanβ,因此OX轴上的速度uJ、uS及vK叠加可求得射流速度vJ和杵体速度vS为
(3)
1.2 超聚能机理
1.2.1 提高射流有效质量
在传统聚能装药结构中,只有部分靠近药型罩的内层材料形成对穿深贡献的射流,而外层材料的大部分形成对穿深基本无贡献的杵体。能否设计一种新型聚能装药结构,使得形成射流的药型罩内层材料转化为杵体,形成杵体的药型罩外套材料形成射流,且其形成射流的速度能够达到传统射流的速度,即形成射流速度高、用于侵彻的有效质量大的超聚能射流,达到对防护装甲高效毁伤的目的。
若将(1)式、(3)式中的压合角β增大到它的互补角β′=π-β,可得:
(4)
(5)
当压合角增大到它的互补角时,对比(1)式、(4)式可知,原来的射流质量和杵体质量发生了互换;对比(3)式、(5)式可知,原来的射流速度和杵体速度也发生了互换。这就意味着实现了药型罩的外层材料形成射流,药型罩的内层材料形成杵体,从而提高了射流的有效质量,但形成射流的速度降低了。
1.2.2 提高射流速度
超聚能装药结构可以在提高射流有效质量的基础上,保证射流的速度不降低。典型超聚能药型罩主要由截顶药型罩及附加装置两部分组成,如图4所示,附加装置为圆柱形,质量为mab,密度为ρab,直径为Dab,壁厚为δab;药型罩质量为ml,密度为ρl,口径D,截顶直径为Dl,壁厚为δl,锥角为2α(α<90°)。在理想状况下,爆轰波同时冲击附加装置及药型罩与炸药接触的全部表面,附加装置及药型罩与炸药接触的单位表面积S所受到的冲量I相等,单位体积(立方体)附加装置与药型罩质量分别为m′ab、m′l,药型罩压合角β与半锥角α相等。附加装置的速度为vab方向与OX轴正方向一致,药型罩的压合速度v0方向与药型罩表面垂直,与上述1.1节传统聚能射流形成理论一致,速度v0可以分解为沿罩母线方向的分量u0和沿OX轴正方向的分量vK,其相互关系见(2)式。
由
(6)
可得vab与v0具有如下关系:
(7)
记
(8)
则
vab=f×v0.
(9)
由于射流碰撞过程是对称的,取射流半平面作为研究对象,如图5所示。药型罩在爆轰波作用下压垮,射流作用于附加装置,改变了射流的速度方向,射流在中轴线处发生大角度碰撞、形成超聚能射流。为了方便研究,引入一个具有恒速运动的坐标系,其原点由O点沿OX轴正向运动,运动速度为vab,图5(a)为截顶药型罩与附加装置碰撞形成的贴壁射流示意图,忽略截顶药型罩在附加装置推动作用下的响应时间,即截顶药型罩瞬时达到附加装置速度vab,此时在动坐标系下,射流沿OX正向的速度为
vX=vK.
(10)
碰撞瞬间将碰撞区域作为刚性处理,因此由(1)式、(2)式可知:

(11)
在射流继续与附加装置碰撞并沿其壁面流动过程中,由于爆炸焊接等问题,射流存在一定的速度损失,设其损失系数为f(λ),λ为相关系数,其与附加装置及药型罩碰撞速度、材料声阻抗等参数有关,则射流沿OY轴负方向运动速度为
vY=f(λ)×u′J.
(12)
将90°-β代入(4)式可得,截锥药型罩与附加装置碰撞时产生的射流质量m′J与杵体质量m′S为
(13)
在静止坐标系中,杵体质量m′S的轴向速度为
v′S=vK+vab=[1/sinβ+f]v0.
(14)
图5(b)为射流与OX轴刚性碰撞示意图,射流来流速度为
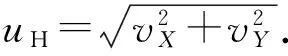
(15)
压合角为
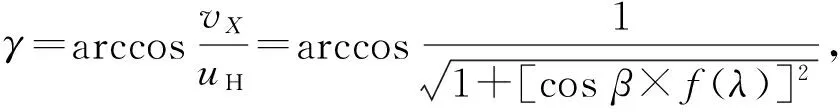
(16)

(17)
由(1)式可知:
uJ=uS=uH.
(18)
回到静止坐标系中,射流的轴向速度为
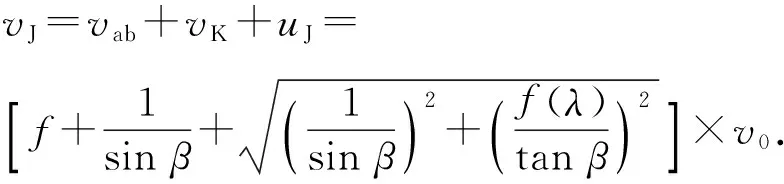
(19)
此时杵体的速度为

(20)
由于附加装置速度vab大于杵体速度vS,杵体在附加装置二次推动作用下最终速度为
vS=vab=f×v0.
(21)
由(14)式、(19)式、(21)式得,超聚能射流截顶药型罩各部分速度分布为
(22)
将γ代入(4)式可得射流mJ与OX轴刚性碰撞时产生的射流质量mJ与杵体质量mS为
(23)
由(13)式、(17)式、(22)式得,超聚能射流截顶药型罩各部分质量分布为
(24)
1.3 超聚能射流与传统射流对比分析
图6为截顶药型罩示意图。由几何关系可知,截顶药型罩质量ml(图6阴影部分)与原药型罩质量m存在如(25)式所示关系:
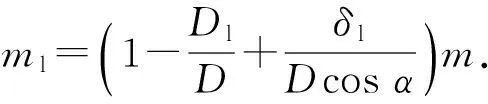
(25)
基于上述理论对超聚能射流与传统射流速度、质量关系进行对比研究,附加装置及药型罩参数如表1所示。

表1 附加装置及药型罩参数
将表1中参数代入(25)式得:
ml=0.695m.
(26)
将表1中参数代入(1)式、(3)式得,传统聚能装药射流、杵体质量及速度为
(27)
将表1中参数代入(8)式、(22)式、(24)式、(26)式,同时假设f(λ)=1,得超聚能射流截顶药型罩各部分质量及速度分布为
(28)
在表1所示工况中,超聚能射流速度为相同壁厚、相同锥角下的传统聚能射流的1.32倍,质量为传统聚能射流的6.84倍。由超聚能射流速度及质量公式(22)式、(24)式可知,参数f、f(λ)及β是超聚能射流及质量分布的主要影响因素。
在表1所示工况中,假设f(λ)=1,半锥角15°≤β≤45°时,超聚能射流速度及质量随着β变化规律如图7所示。与传统聚能装药射流速度随着β角度变化规律一致,随着β角度的增大,超聚能射流速度逐渐减小;当角度β值相同时,随着f增大,超聚能射流速度增大,如图7(a)所示。超聚能射流质量随着角度β值的增大而增大,如图7(b)所示,在理想状况下,超聚能射流质量大小与f值无关。因此参数β、f存在最优值,同时可以针对不同目标通过调节β、f取值获得需要的射流速度与质量。
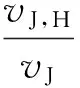
2 数值模拟研究
采用非线性显式动力学分析软件AUTODYN,对在表1所示工况超聚能射流及其对应的传统聚能射流进行数值模拟,其初始模型如图9所示,在药型罩口部设置固定观测点,用以测量流过口部位置射流速度的变化。药型罩口部传统射流与超聚能射流速度对比如图10所示,超聚能射流与传统聚能射流速度最大值分别为11 175.4 m/s、7 808.7 m/s,超聚能射流速度为传统聚能射流的1.43倍,上述理论公式(27)式、(28)式计算结果为1.32倍,二者的偏差为8.3%;数值模拟结果表明,超聚能射流与传统聚能射流杵体速度基本相同,与上述理论公式(27)式、(28)式计算结论基本一致。
典型超聚能射流形成过程如图11所示,爆轰波首先作用于附加装置,截顶药型罩在附加装置推动作用下获得一定的初始速度;在爆轰波作用下,药型罩开始压垮,沿附加装置形成贴壁射流(见图11(b)),此过程对应理论模型中的图5(a)阶段;贴壁射流在截顶药型罩轴线处发生碰撞(见图11(c)),产生超聚能射流,此过程对应理论模型中的图5(b)阶段;超聚能射流进一步拉伸变形,最终形成如图11(e)所示速度高、质量大的超聚能射流。
3 试验验证
试验超聚能装药结构几何参数如表1所示,传统聚能装药结构几何参数与超聚能结构参数相同,只是将附加结构材料改为药型罩材料且与药型罩加工为一体。图12为超聚能与传统聚能射流试验及数值模拟结果对比图。由表2、表3数值模拟结果与试验结果对比可知,靶板入口直径数值模拟结果与试验结果最大偏差为6.9%,靶板侵彻深度数值模拟结果与试验结果最大偏差为5.0%,数值模拟结果与试验结果对比,二者基本一致,说明研究中采用的计算方法、材料模型及相关参数等是合理的。对比传统聚能射流与超聚能射流侵彻试验结果可知,在2.5D炸高工况下,超聚能射流的侵彻深度为传统聚能射流的2.3倍。

工况入口直径侵彻深度试验值计算值误差/%试验值计算值误差/%2.0D77.080.03.996.092.0-4.22.5D50.050.0087.090.03.4
4 结论
1) 理论推导结果表明,附加装置材料、厚度、直径和截顶药型罩截顶高度、锥角、材料等参数均对超聚能射流速度及有效质量具有重要影响,在进行超聚能射流设计时需优化考虑以上参数的配合关系。
表3 超聚能装药侵彻数值模拟结果与试验结果对比
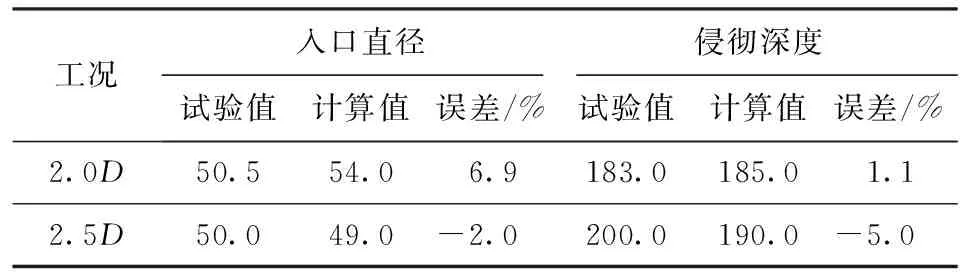
Tab.3 Comparison of numerical and experimental results of hyper shaped charge mm
2) 随着药型罩锥角的增大,超聚能射流速度逐渐减小、质量增大;锥角相同时,随着f增大,超聚能射流速度增大,在理想状况下,超聚能射流质量大小与f值无关。
3) 超聚能射流速度理论公式计算结果与数值模拟结果吻合较好,说明给出的理论推导过程具有较高的可信度。
4) 理论公式、数值模拟及试验结果表明,超聚能射流速度及有效质量远大于传统聚能射流。
)
[1] 隋树元,王树山. 终点效应学[M]. 北京:国防工业出版社,2000.
SUI Shu-yuan, WANG Shu-shan. Terminal effect [M].Beijing: National Defense Industry Press, 2000. (in Chinese)
[2] 张晓伟,段卓平,张庆明. 钛合金药型罩聚能装药射流成型与侵彻实验研究[J]. 北京理工大学学报,2014, 34(12):1229-1233.
ZHANG Xiao-wei, DUAN Zhuo-ping, ZHANG Qing-ming. Experimental study on the jet formation and penetration of conical shaped charge with titanium alloy liner [J]. Transactions of Beijing Institute of Technology, 2014, 34(12):1229-1233. (in Chinese)
[3] 闫玉凤,陈智刚,鲁修国,等. 两种典型串联聚能射流的数值模拟[J]. 弹箭与制导学报,2011, 31(1):88-90.
YAN Yu-feng, CHEN Zhi-gang, LU Xiu-guo, et al. Numerical simulation of two typical tandem shaped charge jet [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(1):88-90. (in Chinese)
[4] Minin V F, Minin O V, Minin I V. Physics hypercumulation and combined shaped charges[C]∥ IEEE International Conference on Actual Problems of Electronics Instrument Engineering. Novosibirsk, Russia:IEEE, 2013:71-89.
[5] 王成,钱俊松,王万军. 超聚能射流形成的数值模拟 [C]∥北京力学会第20届学术年会.北京:北京力学会,2014.
WANG Cheng, QIAN Jun-song, WANG Wan-jun. Numerical simulation of hyper-accumulation shaped charge formation[C] ∥the 20th Annual Academic Conference on Beijing Society of Theoretical and Applied Mechanics. Beijing, China: Beijing Society of Theoretical and Applied Mechanics,2014. (in Chinese)
[6] 钱俊松. 超聚能装药结构优化设计及其形成机理的数值模拟研究[D]. 北京:北京理工大学,2015.
QIAN Jun-song. Numerical simulation of optimum design for hyper-accumulation shaped charge and its jet formation mechanism [D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)
[7] 王淦龙. 超聚能射流数值模拟的初步研究[D]. 北京:北京理工大学,2015.
WANG Gan-long. Elementary study of numerical simulation on hyper-accumulation [D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)
[8] 李庆鑫,王志军,陈莉,等. 一种超聚能装药结构的仿真[J]. 兵器装备工程学报,2016, 37(6):35-38.
LI Qing-xin, WANG Zhi-jun, CHEN Li,et al. Simulation research of a super shaped charge structure [J]. Journal of Ordnance Equipment Engineering, 2016, 37(6):35-38. (in Chinese)
[9] Л П. 奥尔连科. 爆炸物理学[M]. 孙承纬, 译. 第3版. 北京:科学出版社,2011.
Opлehko Л П. Explosive physics [M]. SUN Cheng-wei, translated. 3rd ed. Beijing: Science Press, 2011. (in Chinese)

