发射药燃烧热辐射传播规律*

王艳平,曾 丹,张同来,李素灵,刘 英,王永涛

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081;2.中国兵器工业集团兵器工业安全技术研究所，北京 100053;3.西安北方惠安化学工业有限公司，陕西 西安 710302)

热辐射毁伤是火灾、燃烧的主要危害因素[1]，也是发射药生产与储存安全生产事故的主要破坏效应之一。因此，研究发射药燃烧热辐射传播规律，对预估发射药燃烧毁伤范围、研究其防殉燃距离、确定发射药生产与储存过程中的安全防护等[2]具有重要意义。针对不同物质燃烧的热辐射毁伤的研究均基于球体燃烧模型，如用于气体爆炸或液体燃烧场的ILO模型[3]、Roberts模型和BLEVE模型[4]；用于含能材料燃烧爆炸场的Hasegawa模型、Sato模型、Baker模型[5]、相似律模型和Waston模型[6]等。但是，通过自由场条件下发射药燃烧实验发现，其燃烧火焰近似呈柱体，与传统燃烧爆炸球体模型的认知差异较大。

为了真实反映自由场条件下发射药燃烧火焰的客观情况，本文中拟构建发射药柱状燃烧热辐射物理数学模型，并开展自由场条件下单基发射药燃烧实验研究，对比分析相似律模型和Waston模型等2种球体燃烧模型，进而说明出柱体燃烧热辐射模型更符合单基发射药燃烧热辐射传播规律。

1 构建物理数学模型

构建发射药柱状燃烧热辐射物理数学模型，主要基于燃烧理论和能量守恒定律，在忽略燃烧热辐射过程中热传导和对流等热能损耗的情况下，结合柱状燃烧火焰形态，按燃烧爆炸放出的热量(即爆热)进行能量转化分析。

1.1 辐射强度与药量的关系

从燃烧理论分析，发射药热辐出度与温度的4次方成正比[7]；从能量角度分析，发射药热辐出度与燃烧速率近似呈线性关系(假定转化效率不变)。设发射药爆热为P0，燃烧速率为v，热能转化为辐射能量的效率为c，则任意时刻，向空间辐射出的总辐出度：

M=cvP0

(1)

当燃烧速率v与药量W呈指数关系时，即：

v=ρWb

(2)

如果ρ为常数，则：

M=cρWbP0

(3)

对柱体模型而言，相同燃烧温度下燃烧速率越高，火焰高度和半径越大，水平方向辐出度的转化效率越小，假设热通量与燃烧速率近似用指数关系来表示，即：

q∝v-a

(4)

则发射药燃烧时热通量与药量W的关系为：

q∝P0Wb

(5)

水平方向的热剂量Q与药量W的关系也可近似表示为：

Q∝P0Wb

(6)

式中：q为距离R处的热通量，W为药量，R为距离，b为燃烧速率与药量之间相关系数。

1.2 水平方向辐射强度与距离的关系

由于发射药柱体燃烧模型在x和y方向的燃烧辐射强度不同，当距离远大于火焰尺寸时，可将火焰近似视为点辐射源，热通量与距离的平方成反比，等同于球体模型；而当火焰尺寸远大于距离时，可将火焰近似视为无穷长圆柱，则热通量与距离成反比。则水平方向的热通量与距离的关系为：

(7)

水平方向的热剂量是热通量对时间的积分，可表示为：

(8)

式中：a1、a2、α1、α2为常数。

1.3 热辐射水平方向传播的数学模型

由热辐射理论可知，不同距离处的热通量与辐射源的辐射强度成正比，根据式(6)、(7)，可得发射药燃烧时水平方向热通量为：

(9)

对于距离火源中心R处的热剂量，与药量、距离呈近似关系：

鲁西集团作为一个拥有40年化肥生产历史的国有企业，他们敢于担当，勇于创新。投巨资先后上马了10万吨尿素硝酸铵溶液、10万吨液体肥、10万吨硝酸铵钙、六大类菌剂产品。

(10)

2 发射药燃烧热辐射实验

2.1 实验方案

测试样品为单基发射药，装药近似呈圆饼状，采用1、3、5和10 kg等4种药量，实验温度为17～23 ℃。传感器测量面垂直于热辐射水平传播方向，测点位置沿水平方向呈直线布置，且测点1至测点7距火焰的距离分别为3、4、5、6、8、11和15 m，实验布置见图1。

2.2 实验测试系统

实验测试系统由热通量传感器、高精度放大器和数据采集仪等组成，其中热通量传感器(VATELL公司HFM/6D型)响应时间最长为10 ms；配套的放大器(AMP6型)增益为5 000，带宽25 kHz。

3 实验数据分析

3.1 药量与燃烧速率的关系

在自由场实验条件下，研究单基发射药燃烧时间随药量变化的关系，得到不同药量下的平均燃烧时间和单基发射药燃烧速率，具体数据见表1。

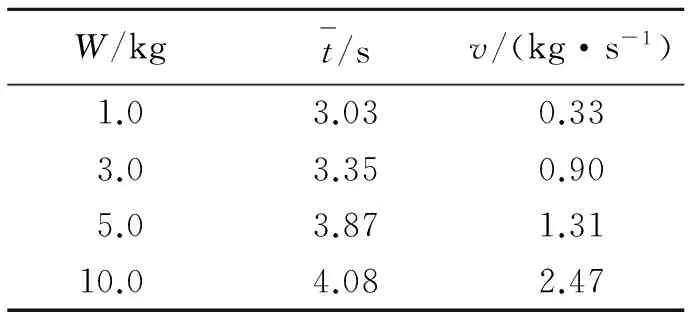
表1 实验数据Table 1 Experimental data

根据表1测试数据，采用指数公式进行数据拟合，得到发射药燃烧速率与药量的关系为：

v=0.205 9W1.222 8

(11)

由图2中可以看出，发射药燃烧速率与药量的函数关系曲线与实验数据基本吻合，证明发射药燃烧速率与药量成指数关系。

3.2 热通量与距离和药量的关系

根据自由场条件下单基发射药燃烧实验测试数据，利用相似律模型、Waston模型和柱体模型等分析热通量理论计算模型，确定各模型参数。

3.2.1相似律模型参数分析

由相似律模型得到：

(12)

3.2.2Waston模型参数分析

由Waston模型得到：

(13)

式中:P0为爆热，t为观测样品燃烧时间。

3.2.3柱体模型热辐射参数分析

由柱体模型数学表达式(式(9))，得到：

(14)

式中:单基发射药爆热P0=3 950 kJ/kg。

基于上述相似律模型、Waston模型和柱体模型等3种热辐射理论模型，利用测试数据对比分析各模型热通量随测试距离、药量变化而变化的情况，具体如图3～4所示。其中，图3反映了在不同药量情况下，热通量随着距离增大而呈快速减小的趋势；图4反映了在不同测试距离条件下，热通量随着药量增加而呈线性增长趋势。综合对比显示，在3种热辐射理论模型中，柱状模型曲线与实验数据吻合性最好，从而验证了柱状模型更能客观反映单基发射药燃烧热辐射传播规律。

3.3 热剂量与距离和药量的关系

根据实验测试结果，利用式(10)对实验数据进行函数拟合，得到柱体模型水平方向热剂量与距离、药量的函数关系式：

(15)

基于柱体模型水平方向的热剂量与距离、药量的定量关系，利用测试数据对比分析热剂量随距离、药量变化而变化的情况，具体如图5～6所示。其中，图5反映在不同药量情况下，热剂量随距离的增大而呈快速衰减态势；图6反映在不同测试距离下，热剂量随着药量增加而呈线性增长态势。综合对比显示，在4种不同药量(1～10 kg)和3种不同距离(3、6和15 m)情况下，基于柱体模型的热剂量与距离、药量的函数关系与实验测量值吻合较好。

4 结 论

根据自由场条件下发射药燃烧火焰形态，按照发射药完全燃烧理论和能量守恒定律，建立发射药柱状燃烧热辐射理论模型，并通过自由场条件下单基发射药燃烧实验，验证了柱状燃烧热辐射理论模型的可行性和合理性。与此同时，通过实验数据分析和函数拟合，得到单基发射药燃烧热通量与距离、药量，以及热剂量与距离、药量等2种热辐射效应定量函数关系式。

[1] 邓金榜.四种温压炸药综合毁伤效应研究[D].南京:南京理工大学,2013.

[2] 廖静林,江劲勇,路桂娥.发射药的火焰燃烧温度计算与测定分析[J].含能材料,2011,19(1):74-77.

LIAO Jinglin, JIANG Jinyong, LU Gui’e, et al. Calculation and measurement analysis of propellant burning temperature[J], Chinese Journal of Energetic Materials, 2011,19(1):74-77.

[3] 涂吉兴,揭业香.LNG储罐组泄漏爆炸事故后果模拟[J].安防科技,2006(11):25-27.

TU Jixing, JIE Yexiang. The simulation of LNG tank leak explosion consequences[J]. Security and Safety Technology Magazine, 2006(11):25-27.

[4] 王玉.液化天然气槽车火灾爆炸危险性分析[J].化工生产与技术,2015(3):50-52.

WANG Yu. Risk analysis on fire and explosion incident of liquefied natural gas (LNG) tanker wogons[J], Chemical Production and Technology, 2015(3):50-52.

[5] 赵志宁,王辰.新型弹药热辐射毁伤效应研究[J].军械工程学院学报,2015,27(1):15-18.

ZHAO Zhining, WANG Chen. Research on damage effect of new type ammunition thermal radiation[J]. Journal of Ordnance Engineering College, 2015,27(1):15-18.

[6] 徐春,张煜盛,徐建新,等.零维模型在二甲醚发动机工作过程中的应用研究[J].柴油机设计与制造,2003(3):9-12.

XU Chun, ZHANG Yusheng, XU Jianxin, et al. The application research on zero-dimensional model in DEM engine work[J]. Design & Manufacture of Diesel Engine, 2003(3):9-12.

[7] 周世椿.高级红外光电工程导论[M].北京:科学出版社,2014:110-111.