基于动态信标生成树的传感器定位算法

赵怡宏，王赜，张海娟

天津工业大学计算机科学与软件学院，天津300387

基于动态信标生成树的传感器定位算法

赵怡宏，王赜，张海娟

天津工业大学计算机科学与软件学院，天津300387

CNKI网络出版：2017-03-13,http://kns.cnki.net/kcms/detail/11.2127.TP.20170313.1638.022.html

1 引言

近年来，随着微机电系统（MEMS）、无线通信技术及传感器技术的发展和相互融合，无线传感器网络（Wireless Sensor Networks，WSNs）[1-2]日趋成熟。WSNs是集信息采集、传输、处理于一体的综合智能信息系统，具有广阔的应用发展前景。传感器节点具有传感、驱动控制、计算及通信能力，能够实时监测、感知和采集目标区域中监测对象的各种信息，从而实现计算机世界、物理世界以及人类社会三元世界的连通[3-5]。WSNs凭借其节点体积小、成本低、功耗低、自组网络等优势，已被广泛应用在军事领域、环境监测、工农业、生物医疗、智能交通等各个领域[6-8]。

现有的理论成果有效地推动了相关研究的发展，在无线传感器定位方面，文献[1]和文献[2]首先描述了无线传感器网络的定位基础知识，着重介绍了无线传感器网络生命周期，能量消耗，节点移动速度等因素对传感器节点定位的影响。文献[9]引入了移动信标节点辅助定位机制，这是一个典型的方法，通过使用有限数量的移动信标节点大大降低了网络的部署实施成本。文献[10-11]介绍了一种anchor-guiding机制，通过规划信标节点的移动路径，有效地引导移动信标节点沿着一个有效的路径移动，从而节省定位所需的时间。文献[12]提出了DREAMS算法，在该算法中信标节点的移动信标节点借助图的深度优先遍历（DFT）思想来规划路径。

在监测区域中，无线传感器节点往往是通过抛撒的方式来随机部署的，导致的结果就是传感器节点的分布往往是疏密不均的。以往的对信标节点移动路径进行规划的算法[9]大多把研究方向放在如何通过规划路径来覆盖更多的区域，以此来确保更高的定位率，这样整体的定位率虽然得以提高，但是定位时间、定位精度和能量开销的优化无法同时得到有效保证。再者，现有的算法并不把网络节点密度作为定位的参考依据。如此一来，在节点分布少的区域和节点分布密集的区域采用相同的定位方法，就会导致节点分布密集的区域定位精度低，节点分布相对较少的区域定位率低下，信标节点能量得不到最大化利用等问题的产生。

针对上述问题，文中提出了基于网络节点密度来定位的生成信标树算法（GBT）。GBT算法的主旨思想主要来源于图的深度优先遍历（DFT），在网络中构建一个信标节点组，通过对当前信标节点广播区域内传感器节点的一跳未被定位的邻居节点的个数的比较，在网络中动态生成一棵深度优先信标树（DFBT），以此来规划信标节点组的移动路径，从而达到全网节点的精确定位。

通过仿真实验，证明了GBT算法在节点定位精度，定位时间和信标节点能量的最大化利用等问题上都具有比其他规划信标节点移动路径算法有更好的优越性。

2 传统的动态信标节点辅助定位算法

动态信标节点可以在网络中任意移动，通过使用内嵌的GPS或者其他定位系统对自己的位置进行感知，然后在网络中以特定的频率或在设计好的位置进行包含自己地理位置信息的信标信息的广播[10-11]。网络中的待定位普通传感器节点通过接收信标节点广播的信标信息对自己进行定位[13]。

2.1 Snake-like算法

Snake-like算法[14]，利用一个移动信标节点，它的开始位置被设置在监测区域的左上角，然后向下呈直线状在监测区域内进行遍历，到达下边界后向右转向，移动一定距离后，再向上呈直线状行走，如此反复，直到信标节点的遍历路径已经完全覆盖整个监测区域或者信标节点的能量耗尽而不得不停止移动。图1描述了Snakelike算法的遍历方式。

图1 信标节点在监测区域内使用Snake-like算法生成的遍历轨迹

在监测区域较小时，该算法可以完成对整个监测区域的遍历，但如果监测区域较大时，信标节点的能量往往在移动过程中就会被消耗殆尽。如此一来，信标节点的能量是确定的，那么两条遍历轨迹间的距离就决定了信标节点遍历所能覆盖的监测区域面积。

2.2 Random-walk算法

Random-walk算法，该算法模型较为简单，将信标节点随机部署在一个监测区域内。将信标节点的移动速度和信标信息广播包的发送频率设为定值，但是信标节点的移动方向是随机的。

在这种情况下，信标节点的移动轨迹具有随机性，很可能会导致节点一直在同一片区域中打转，造成节点的定位效率具有很大的波动性，那么定位效率就完全取决于信标节点移动轨迹所能覆盖的监测区域面积。

针对传统动态信标节点辅助定位算法存在的问题，本文引入了基于节点密度的定位算法。下一章将对该算法进行详细的介绍。

3 动态信标生成树算法

3.1 网络模型描述

假定大量静态普通传感器节点被随机抛撒在监测区域内，同时将一个包含四个信标节点的信标节点组部署在网络的正中心。普通传感器节点无法直接获取自己的位置信息，需要信标节点来对其进行辅助定位[15-16]。所有网络节点的通信半径均为r。信标节点的通信半径可根据定位需求情况进行相应改变。为了计算方便，定位过程中将节点的圆形通信区域的外接正方形确定为节点定位的约束区域范围。比如t时刻信标节点在坐标(x,y)处以r为半径进行广播，通过建立平面直角坐标系来进行描述，数轴的正方向设为向上和向右的方向，则该信标节点所能形成的广播约束区域在[(x-r,y+r),(x+r,y-r)]t内。

网络中的每个节点都会有自己唯一相应的ID，以此来对不同的传感器节点进行区分。通过发送“Hello”信息，传感器节点以此来维护它们之间的邻居关系。在定位过程中，传感器节点之间会发送含有特定定位信息的message以此来进行定位[12]。

3.2 算法设计

基于节点密度定位算法的主旨思想是：根据网络节点密度分布，规划信标节点组的移动路径，从而完成对网络中所有节点的精确定位。该算法主要借鉴的思想是图的深度优先遍历（Depth-First Traversal，DFT），设计了生成信标树算法（Generate Beacon-based Tree，GBT），在网络中动态地生成一棵深度优先信标树（Depth-First Beacon-based Tree，DFBT），从而指导信标节点组进行移动。这棵信标树上除根节点root外的其余节点，均需要调用估计位置算法（Estimate Location，EL）和信标节点组移动算法（Beacon Group Moving，BGM）。

3.2.1 选举root节点

网络初始化时，首先构造一个以节点通信半径r的2倍为边长的正方形，分别将四个信标节点放置在正方形的四个顶点上，组成一个信标节点组，并将该正方形放置在网络的中心位置。这四个信标节点可以任意移动，当且仅当任一信标节点的广播半径内存在有数量大于1的未被定位的普通传感器节点后，信标节点组停止移动。确定这个通信范围内具有普通节点数大于1的信标节点的位置，以此位置的坐标为中心，以r为半径广播信标信息，从而形成广播约束区。指定该信标节点为根信标节点（root），也就是DFBT的根节点。

如果信标节点在相同时刻发现存在数量大于1的未被定位的普通节点，则通信范围内节点数最多的信标节点被指定为root；如果发现时间和数量都相同，则随机选取任一信标节点为root。

3.2.2 估计位置算法

在找到root节点后，在生成信标树的过程中还需要使用估计EL算法。EL算法可以分为以下三个步骤：

（1）确定目标统计区域（Object Statistical Area，OSA），找出下级目标信标节点（target beacon）。

（2）确定target beacon的估计区域。

（3）计算target beacon的估计位置。

为了实现以网络节点密度为参考依据来对全网节点完成定位，GBT算法需要统计对比current beacon的OSA内，普通节点周围未被定位的一跳邻居的数量，从而保证信标节点组总是朝着待定位节点分布最为稠密区域的方向移动。current beacon代表的是当前需要广播信标信息来辅助定位的普通传感器节点。

统计OSA内普通传感器节点周围未被定位的一跳邻居的个数，current beacon对个数进行比较，找出其中的最大值。指定这个最大值节点为target beacon。在确定target beacon的估计位置后，它会成为新的current beacon，与此同时形成新的OSA，再次统计新的OSA内普通传感器节点周围未被定位的一跳邻居节点的个数。以此类推，直至终结。

注意到，当target beacon的估计位置与current beacon所在的位置比较相近时，它升级为current beacon后形成的新的OSA与原来的上级current beacon的OSA重合区域会比较多。这就会导致只有少量新的未被统计过一跳邻居数量的节点添加到新的OSA内，将会使信标节点组向网络节点分布稠密区域移动的速度大大减弱，进而影响全网节点定位所需的时间成本。

为了避免或减小这样的情形，将具有相同质心的、边长为r的正方形区域从current beacon构建的广播约束区域中剔除掉，如图2所示，用OSA来表示剩余的阴影区域。

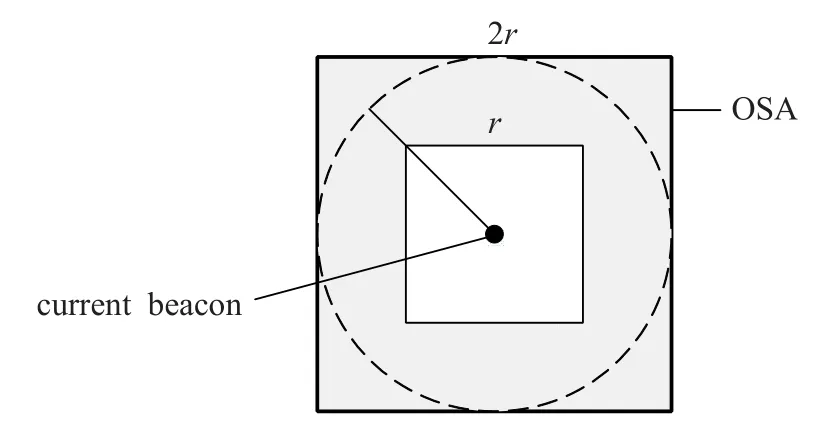
图2 current beacon形成的OSA

接下来要对target beacon的估计位置进行确定。在OSA区域的四个顶点上分别放置信标节点，然后分别以四个顶点为中心，以r为半径广播信标信息。这时，普通传感器节点在current beacon广播约束区域内的估计约束区域将减小到3r×r，并将拥有一跳邻居数最多的传感器节点范围确定在大小为的区域内。

当current beacon为root节点时，可以得出EL算法的执行次数和target beacon估计区域之间的关系，如表1所示。

假设当前target beaconS′使用EL算法得到的估计位置坐标为(xest,yest)，其真实的位置坐标为(xreal,yreal)，则可以用式（1）来表示节点S′的定位误差：

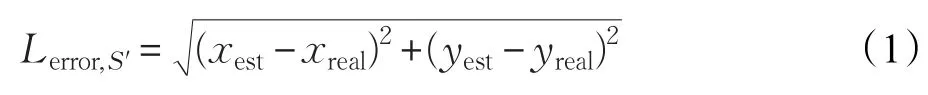
表1 当current beacon为root节点时，EL算法的执行次数n和target beacon估计区域大小之间的关系

3.2.3 信标节点组移动算法

在对target beacon进行定位的过程中，信标节点组的移动是具有一定规律的。确定下一时刻信标节点组用于广播信标信息的位置需要以下几方面因素：当前形成target beacon所在估计区域的信标节点的坐标，当前信标节点组所在正方形区域的中心坐标，以及当前信标节点组用于广播信标信息的半径之间的关系。在本文中，将这种算法叫作信标节点组移动算法BGM。用一个三元消息串来表示用于确定信标节点组下一时刻位置的信息，记作其中“||”表示消息串联，表示当前形成target beacon所在估计区域的信标节点的坐标，表示当前信标节点组所在的正方形区域的中心坐标，表示当前信标节点组用于广播信标信息的半径。

在本文中，形成的约束区域的顶点的坐标，用有序组V来表示，记作V v1,v2,v3,v4,…；在约束区域顶点处广播信标信息的信标组的有序集合，用有序组B来表示，记作B b1,b2,…,bi；相应于有序组B中的信标节点组的坐标的有序集合，用有序组G来表示，记作G g1,g2,…,gi，其中i的范围均为1≤i≤4。有序组中的元素对应于约束区域顶点的顺序是由左到右、由上到下。

初始化网络时，假设root节点为信标节点d，其现在所在的位置坐标为(x,y)。信标节点d以(x,y)为中心，以r为半径进行广播，形成正方形的约束区域。约束区域四个顶点坐标的集合可由信标节点所在位置和通信半径之间的关系得出。假设信标节点组此时以有序组B a,b,c,d在四个顶点处分布，则当四个信标节点分别以当前位置为中心，以r为半径进行广播后，如果图3所示的IV区域中存在一跳未被定位邻居传感器节点的数量最多，则根据BGM算法，用于确定信标节点组下一时刻位置的信息为由此可以得出下一时刻信标节点组将在坐标处广播信标信息。如果信标节点在移动过程中遵循就近原则，可以使信标节点组中的每个信标节点，移动路径最短并且减小信标节点的能量消耗。在图3中，current beacon d的OSA是一个方形环，该方形环是由边长为2r，去掉具有相同质心、边长为r的正方形得来的，所以在IV区域对target beacon的定位只需放置三个信标节点在顶点处。依照就近原则，信标节点b和c分别在正方形边长上移动长度为r的距离，保持信标节点d位置不变，可以得到节点信标组下一时刻，以为通信半径广播信标信息的有序组为B b,c,d。

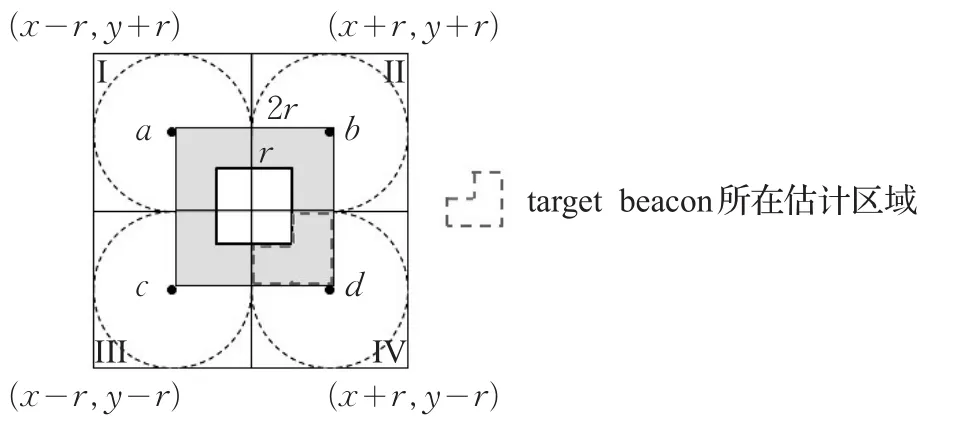
图3 假设target beacon当前位于由信标节点d形成的IV约束区域内

3.2.4 生成信标树算法

以上的算法描述了生成DFBT上的一个节点的过程，接下来详细描述一下怎样在网络中生成一棵完整的DFBT。

算法循环：

步骤1统计current beacon S通信区域内包含的普通传感器节点未被定位的一跳邻居节点的个数，汇总上报给current beacon S，经过比较，S找出拥有一跳未被定位邻居数最多的节点S′，将S′指定为S的target beacon，即S′为S的目标孩子节点。

步骤2执行EL算法，确定S′可能所在的区域，并将S′的估计位置放置在估计区域的质心。升级S′为S。

步骤3重复以上步骤，直至S通信范围内不存在普通传感器节点拥有一跳未被定位邻居节点后停止，即当前信标节点S为这棵DFBT的叶子节点。

步骤4此时S将指向它的parent节点，即上级current beacon节点，查看它的parent节点的通信范围内的S′，对其执行EL算法。

步骤5当S发现自己没有parent节点时，即S为root节点，算法终止。

生成信标树算法主旨是利用深度优先遍历的思想遍历所有节点，所以其算法主要时间复杂度集中在深度优先遍历上，由此可得其时间复杂度大致为O()n，其中n为传感器节点的个数。

网络初始化时，S在root节点处开始，根据DFT思想，通过不断地执行EL算法，在此过程中会生成一棵DFBT。当全网节点都实现定位后，S会再回到root节点的位置。

在执行EL算法时，S′周围的未被定位的传感器节点存在被定位的可能，这就会造成S通信范围中的普通传感器节点的未被定位的一跳邻居节点数量处在一种变动的状态中；而对于已经形成估计区域的传感器节点，其估计区域的大小可能会随着EL算法的执行而减小，而这些并不通过执行EL算法来减小估计区域的传感器节点，在接下来的定位算法中很可能被升级为target beacon，并用来进行辅助定位。综上所述，为了减少定位时间成本和计算开销，在S通信范围内的每个有一跳未被定位邻居节点的传感器都会被生成一条记录，在该记录中存储当前未被定位的一跳邻居节点的个数和当前形成的估计区域的范围。在执行EL算法时，一旦发现S通信范围内的节点拥有的一跳未被定位的邻居节点数量减少或者其相应的估计区域减小，就将变化动态地记录下来。图4描述了生成DFBT算法的基本流程。

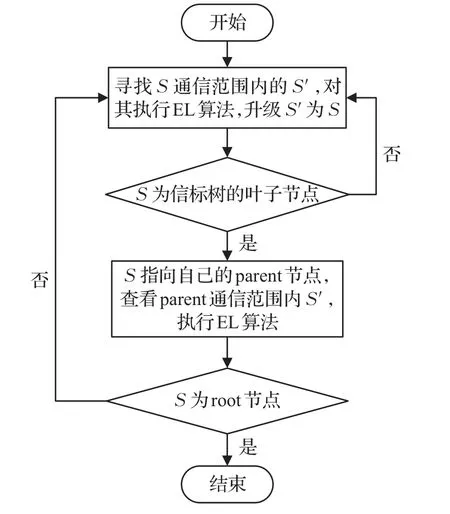
图4 生成DFBT算法的基本流程

4 仿真实验及分析

本章将对前面提出的GBT算法性能进行相关仿真测评。与之比较的算法是：Snake-like算法和Randomwalk算法。

4.1 仿真环境设置

网络仿真环境设置如下：监测区域的大小为500×500units，其中随机分布的传感器节点的个数为100～300。网络初始化时，在监测区域的中心放置信标节点组，并将其移动速度设为定值。网络中所有传感器节点的通信半径均被设置为50。在何时广播信标节点信标信息和普通节点何时发送message的问题上，GBT算法中有相应的规定，但是在Snake-like和Randomwalk算法中，并没有对信标节点和普通节点做出相应要求，为了模拟实际情况，假定信标节点的广播信息和普通节点的messages都以相同的频率发送，设定发送时间间隔为1+θ个仿真单位时间，θ的值是随机的，取值范围为[]

-0.3,+0.3。为了提高实验结果的准确性，在完成对网络中传感器节点的随机部署后，每次都要将算法执行50次，取其平均值进行比较。在执行Snake-like算法时，通过设定参数δ，用来调整Snake-like两条遍历轨迹之间的距离。

4.2 算法性能分析

（1）节点定位率随定位时间的变化

如图5所示，从整体来看，本文提出的GBT算法在定位率上要优于Snake-like算法和Random-walk算法，并且最终总能达到全网定位。

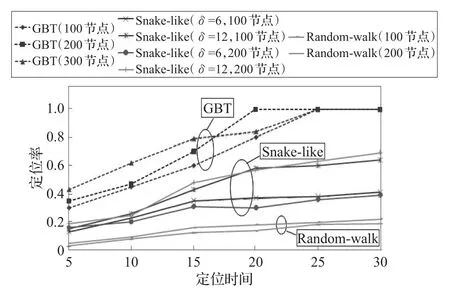
图5 节点的定位率随定位时间增加的变化趋势

这是因为GBT算法是根据节点密度来规划路径的，通信范围内节点的密度越大，每次被定位的节点的数量就越多，相应的定位率也就越大。

Snake-like算法，信标节点能量一定，导致能够遍历的路径长度是一定的。因此，δ的值越大，遍历路径能够覆盖的监测区域的面积就越大，能够被定位的传感器节点的个数也就越多，定位率也随之增高。Randomwalk算法是三个算法中定位率最小的一个，并且此算法定位率的增长趋势又是最无规律的一个，因为它的定位完全是随机的。

（2）信标节点移动总距离

如图6所示，对于本文提出的GBT算法，随着传感器节点密度的增加，信标节点移动轨迹的总长度趋于定值，这是由GBT算法的定位机制造成的。该算法的每次定位都是利用信标节点广播信标信息所构成的约束区域进行的，所以当节点密度达到某一数值后，所生成的DFBT的深度和各层所有节点的度数之和都会趋于定值，导致信标节点的移动轨迹总长度也会趋于水平，达到定值。

图6 信标节点的总移动距离随节点密度增加的变化趋势

对于Snake-like算法，信标节点所拥有的能量值是确定的，其移动路径也是提前规划好的。所以，无论传感器节点在网络中如何分布，信标节点所能移动的距离都是固定的。理论上讲，Random-walk算法移动距离应该与Snake-like算法相等。但从实验结果来看，Randomwalk算法信标节点移动轨迹的总距离总是小于Snake-like算法的，并且其值不固定，会上下波动。这是Randomwalk中信标节点的不定向移动消耗能量造成的。

（3）定位精度

为了表示全网的定位精度，使用平均定位误差来刻画算法的定位精度，同时为了计算简便，对公式（1）做出了简化处理，表示为这里的m指的是网络中传感器节点的个数。

如图7所示，从整体上看，在定位精度上Snake-like和Random-walk算法是要低于GBT算法的。虽然三种算法定位的方式都是基于约束条件的，但GBT算法使用的是信标节点组，并且信标节点组广播信标信息的半径是可变的，所以在信标节点组对target beacon进行定位时，可变的信标广播半径增加了约束区域的多样性，所以处在这些信标节点组周围的普通传感器节点的定位精度会更高。GBT算法的定位精度受target beacon估计位置的影响，执行EL算法的次数n越大，target beacon的估计位置越精确，继而全网节点的定位平均错误率就越低，定位精度也就越高。对于Snake-like和Random-walk算法，随着网络中传感器节点密度增大，随之变化的是平均错误率也在提升。而对于Snake-like算法，通过遍历覆盖的监测区域面积大小与δ有关，随着δ值的增长，覆盖区域越大，其间能够定位的传感器节点数就越多，平均定位错误率相对较低。

（4）节点定位率与信标节点能量开销的关系

如图8所示，通常情况下，节点定位率会随着信标节点广播信息次数的增加呈上升趋势。信标节点广播信标信息产生的能量消耗和节点在网络中移动产生的能量消耗是传感器节点能量消耗的主要来源。GBT算法虽然也要广播信标信息，但是它们广播信息的位置和移动路径是经过计算的，并不是以某一固定频率不断发送，移动方向不具有盲目性，并且当完成对所有待定位节点的定位后，信标节点随即停止移动，不再产生额外的能量消耗。所以从整体来看，当节点能量消耗一定时，GBT算法的定位率是更加优于Snake-like和Randomwalk算法的，并且随着能量消耗的增加，会呈现出更加明显的优势。对于Snake-like算法，δ的值越大，在相同能量消耗的情况下，定位率会越高。

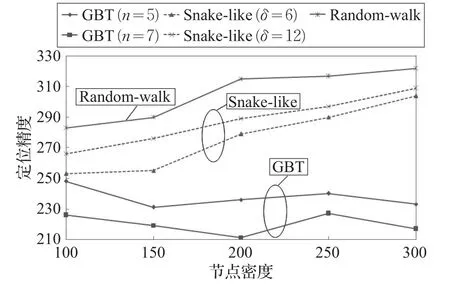
图7 节点的定位精度随节点密度增加的变化趋势

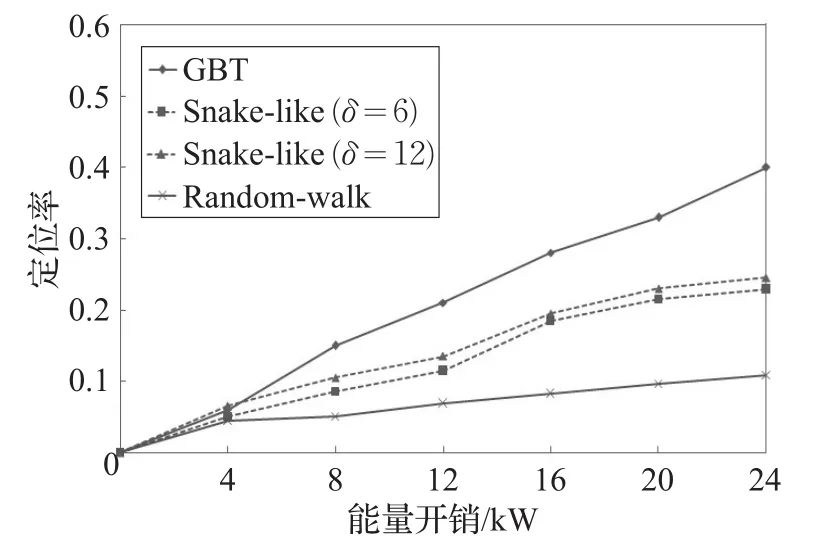
图8 节点的定位率随信标节点能量开销增加的变化趋势

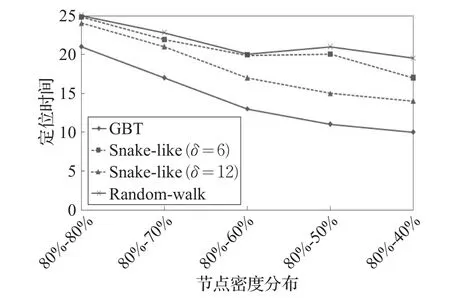
图9 节点的定位时间与网络中节点密度分布的关系

（5）定位速度

如图9所示，在实际环境中Snake-like和Randomwalk算法是无法实现全网络所有节点定位的。所以在这里只讨论在节点密度分布相同的情况下，Snake-like算法达到60%的节点定位率，Random-walk算法达到25%的节点定位率和GBT算法达到全网节点定位各自所需的时间。图9中横坐标表示的是网络中传感器节点的数量与监测区域面积的关系，例如80%-70%表示的是网络中80%的传感器节点分布在70%的监测区域中。

观察图中曲线的走向可以得出，随着网络中节点密度的增加，GBT算法实现全网节点定位所需的时间随之减小，说明定位速度越来越快。在相同节点密度的条件下，Snake-like算法达到60%节点定位率和Random-walk算法达到25%节点定位率所花费的时间是要高于GBT算法达到全网节点定位所花费的时间的，出现这种现象的原因是这两种算法在进行节点定位时，没有将网络中的节点密度作为参考依据，很可能将许多时间和能量都消耗在节点稀疏的区域。δ的值同样对Snake-like算法的定位率有影响，随着δ值的越大，达到相同定位率所需的时间会越短。

5 结束语

文中提出了一种使用动态信标节点组进行定位的自适应算法GBT。该算法中的信标节点组具有可移动性、广播通信半径可变的特点，借鉴图的深度优先遍历思想，通过收集比较网络中节点的一跳未被定位的邻居节点的数量，以此来生成一棵具有动态自适应的深度优先信标树DFBT，通过其来规划信标节组的移动路径。通过该算法可以实现对网络中所有节点的定位工作，并且在节点的定位时间，定位精度和信标节点能量的最大化利用等问题上都有较大的改善。为了进一步地减少定位时间，加快网络的收敛速度，如何在GBT算法的基础上做出改进，论证多信标树协同定位，是接下来要研究的主要任务。

[1] Chen J，Xu W，He S，et al.Utility-based asynchronous flow control algorithm for wireless sensor networks[J].IEEE Journal on Selected Areas in Communications，2010，28（7）：1116-1126.

[2] He Shibo，Chen Jiming，Sun Youxian，et al.On optimal information capture by energy-constrained mobile sensors[J].IEEE Transactions on Vehicular Technology，2010，59（5）：2472-2484.

[3] 景博，张劼，孙勇.智能网络传感器与无线传感器网络[M].北京：国防工业出版社，2011.

[4] 王汝传，孙丽娟.无线传感器网络技术与应用[M].北京：人民邮电出版社，2011.

[5] 余成波，李洪兵，陶红艳.无线传感器网络实用教程[M].北京：清华大学出版社，2012.

[6] Kwon O，Lee E，Bahn H.Sensor-aware elevator scheduling for smart building environments[J].Building and Environment，2014，72：332-342.

[7] Bottero M，Chiara B D，Deflorio F P.Wireless sensor networks for traffic monitoring in a logistic centre[J].Transportation Research Part C，2013，26：99-124.

[8] Bhuiyan M Z A，Wang Guojun，Cao Jiannong，et al.Deploying wireless sensor networks with fault-tolerance for structural health monitoring[J].IEEE Transactions on Computers，2015，64（2）：382-395.

[9] Halder S，Ghosal A.A survey on mobile anchor assisted localizationtechniquesinwirelesssensornetworks[J].Wireless Networks，2015，60（7）：1-20.

[10] Chang C T，Chang C Y.Anchor-guiding mechanism for beacon-assisted localization in wireless sensor networks[J].IEEE Sensors Journal，2012，12（5）：1098-1111.

[11] Cui Huanqing，Wang Yinglong.Four-mobile-beacon assisted localization in three-dimensional wireless sensor networks[J].Computers and Electrical Engineering，2012，38：652-661.

[12] Li X，Mitton N，Simplot-Ryl I，et al.Dynamic beacon mobility scheduling for sensor localization[J].IEEE Transactions on Parallel and Distributed Systems，2012，23（8）：1439-1452.

[13] Guo Z，Guo Y，Hong F，Perpendicular intersection：Locating wireless sensors with mobile beacon[J].IEEE Transactions on Vehicular Technology，2010，59（7）：3501-3509.

[14] Ou C H，He W L.Path planning algorithm for mobile anchor-based localization in wireless sensor networks[J].IEEE Sensors Journal，2013，13（2）：466-475.

[15] Iqbaln A，Murshed M.On demand-driven movement strategy for moving beacons in sensor localization[J].Journal of Network and Computer Applications，2014，44（9）：46-62.

[16] Rezazadeh J，Moradi M，Ismail A S，et al.Superior path planning mechanism for mobile beacon-assisted localizationinwirelesssensornetworks[J].IEEESensors Journal，2014，14（9）：3052-3064.

[17] 邓彬伟，黄光明.WSN中的质心定位算法研究[J].计算机应用与软件，2010，27（1）：213-214.

ZHAO Yihong,WANG Ze,ZHANG Haijuan.Dynamic beacon spanning tree algorithm for sensor localization.Computer Engineering andApplications,2018,54（6）：68-74.

ZHAO Yihong,WANG Ze,ZHANG Haijuan

School of Computer Science&Software Engineering,Tianjin Polytechnic University,Tianjin 300387,China

Node localization in wireless sensor networks is a basic but very important research field.In practical application,sensor nodes are distributed randomly resulting in node density disproportion in the region.The existing localization algorithms of node are not sensitive to distribution density.Hence,if the algorithm applies the same strategy to locate nodes in regions with different node density,it will cause position accuracy low in dense area and location rate decreasing in sparse regions and the beacon node energy is not to maximize utilization.This paper puts forward a spanning tree algorithm of beacon based on node distribution density called GBT.Nodes in beacon group are traversed by planned path to complete node location.The simulation results show that the improved algorithm has better performance on decreasing time expend for locating node,enhancing accuracy of node location by taking advantage of beacon efficiently compared with previous algorithms.

wireless sensor networks;sensor localization;dynamic beacon node;route planning;node density;Generate Beacon-based Tree（GBT）algorithm

节点定位是无线传感器网络中一个基础但十分重要的研究方向。实际应用场景中，传感器节点大多被随机部署，分布往往疏密不均。现存的定位算法对节点的分布密度没有敏感性，如果算法在节点密集区域和稀疏区域使用相同的定位策略，就会造成密度大的区域定位精度低，分布相对稀疏的区域定位率低，信标节点的能量得不到最大化利用等问题。针对这些问题，提出了一种基于节点密度进行定位的生成信标树算法（GBT）。信标节点组沿着规划好的路径对节点进行遍历，实现节点的全定位。通过与其他规划动态信标节点路径算法比较，证明了GBT算法在定位时间、定位精度和对信标节点能量的充分利用上均有所改善。

无线传感器网络；传感器节点定位；动态信标节点；路径规划；节点密度；生成信标树算法

2016-10-31

2017-01-02

1002-8331（2018）06-0068-07

A

TP393

10.3778/j.issn.1002-8331.1610-0392

国家自然科学基金（No.60970016）；天津市自然科学基金（No.11JCYBJC00800）；天津市科技重大专项与工程项目（No.15ZXHLGX00390）。

赵怡宏（1988—），男，硕士，主研领域：无线传感器定位，E-mail：332851167@qq.com；王赜（1976—），男，博士，副教授，主研方向：计算机网络与安全，企业信息化，多媒体通信等；张海娟（1990—），女，硕士，主研方向：无线传感器定位。