基于运动学正解的Delta机器人工作空间分析

韦岩，李冉冉，张鲁浩，周万里，郁汉琪

(南京工程学院 工业中心，江苏 南京 211167)

0 引言

广义的并联机械臂是末端的执行装置由几个独立的运动支链连接到基座，形成的闭环运动链机构[1]。瑞士的Reymond clavel教授于1985年提出的Delta机器人是应用最为广泛的并联机构之一。由于Delta机器人的结构特点，使它只有3个平移自由度，设计、制造、控制都比较简便，在轻工业分拣与包装中应用广泛。机器人的工作空间是衡量机器人工作性能的一个重要性能指标，在进行机构设计、控制、轨迹规划时，工作空间是首先必须要考虑的重要问题。本文介绍一种Delta机器人的结构及工作原理，使用蒙特卡罗方法，在位置正解的基础上，结合MATLAB软件对工作空间进行探索研究。

1 Delta机器人简介

Delta机器人是由动平台、静平台、3根主动臂以及3根平行四边形结构的从动支链组成[2]，结构简图如图1所示。静平台和动平台一般成正三角形，静平台三角形的3边通过3条运动链与动平台三角形的3条边相连。每条运动链都是由4个球铰链与4根杆组成平行四边形，3个电机带动主动臂旋转，进而控制动平台的运动。3组平行四边形采用闭环结构，这保证了动平台与静平台能够始终保证平行，即保证动平台只能进行平动，而不能进行任何方向的旋转。

图1 Delta机器人机构简图

根据Delta机器人的结构及空间机构自由度计算公式[3]来计算其自由度：

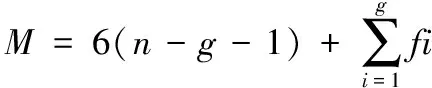
其中：M是自由度，n是机构总的构件数，g是n个构件之间的运动副数目，fi是第i个运动副的相对自由度数，根据公式能够得到Delta机器人的自动度数：

M=6×(17-21-1)+3×6+15=3

2 Delta机器人的运动学模型

2.1 Delta机器人的运动学逆解

机器人的运动学逆解是已知机器人末端在参考坐标系的位姿T的情况下，求机器人各个关节变量qi的取值。运动学的逆解是控制机器人的关键，因为只有各关节变量在按照逆解所求值进行运动时，才能使机器人末端达到目标位置。

首先对Delta机器人模型进行简化处理，由于从动臂运动链呈平行四边形(平面结构)，平行四边形中的2条相对边总是平行，所以平行四边形左右2根杆的运动与上下2边中点连线的运动始终相同，所以简化为图2所示。O为静平台正三角形B1B2B3的中心点，O′为动平台正三角形P1P2P3的中心点，Ei、Pi(其中i= 1,2,3，下同)分别是平行四边形从动臂上下2边的中点，分别在2个平台上建立直角坐标系O-xyz、O'-x'y'z'，且ox⊥B1B3，o’x’⊥P1P3。

设OBi=R，O’Pi=r，则点Bi在坐标系O-xyz中的位置矢量和Pi在坐标系O'-x'y'z'中的位置矢量分别为：

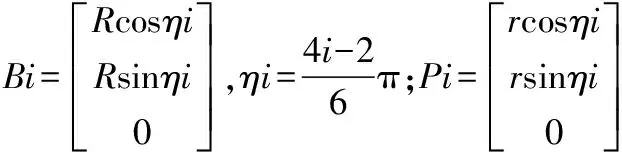
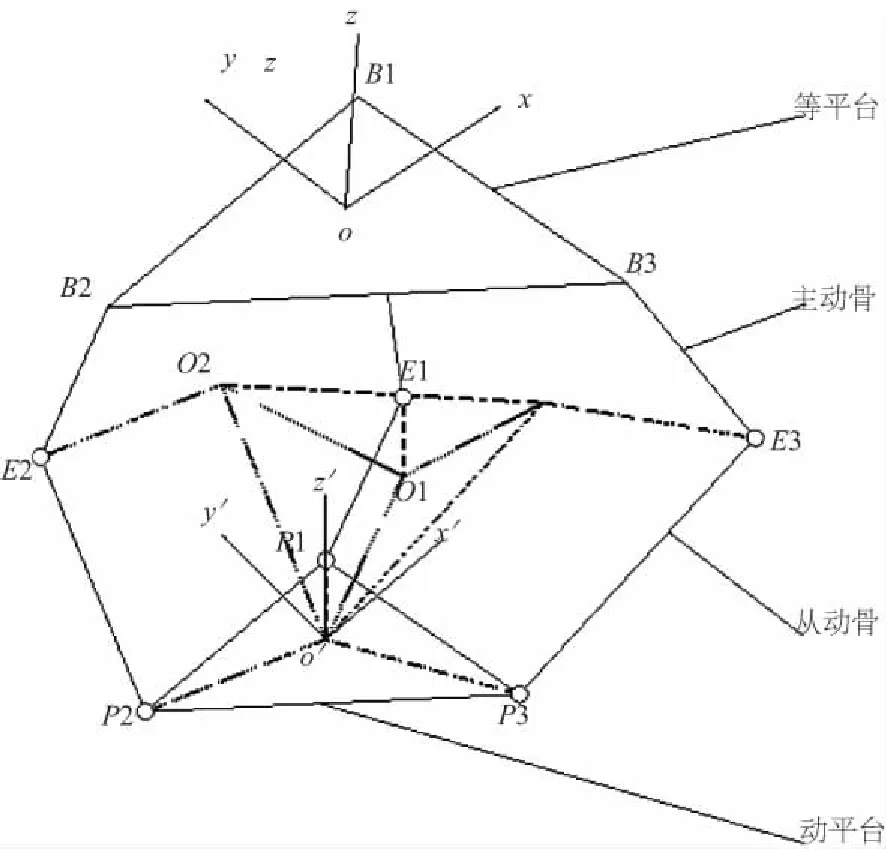
图2 Delta机器人结构示意图

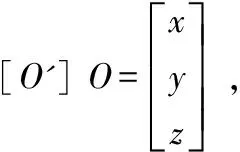
设θi是3根主动臂与静平台之间的夹角，|EiBi|=l1,|PiEi|=l2,则:

得到等式：

[(R+l1cosθi-r)cosηi-x]2+[(R+l1cosθi-r)sinηi-y]2+[-l1sinθi-z]2=l22

(1)

式(1)为运动学逆解公式，即主动臂与静平台张角(输入量)θi与动平台中心点(输出量)位移之间的方程。

化简式(1)，令R-r=Δr，展开得：

(2)

将式(2)写成Acosθi+Bsinθi+C=0

(3)

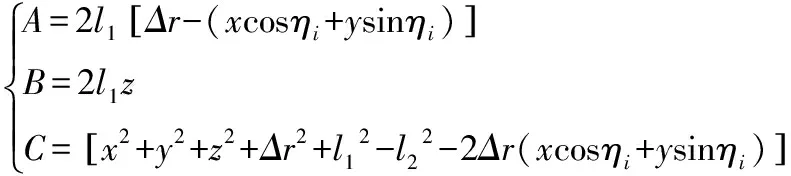
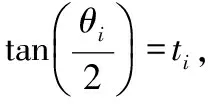
代入式(3)并化简得到：

(C-A)ti2+2Bti+(A+C)=0 (i=1,2,3 )

这是3个一元二次方程,解方程可得

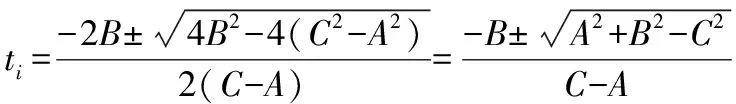
(4)

根据以上公式，当给定动平台的位置坐标时，即可以求出3个主动臂的角度，由于每个方程有2个解，所以逆解共有8组。Delta机器人在运行过程中会受到运动转角的限制，所以并非所有的解都满足要求，结合实际情况选取“±”中的值，即为最终的逆解。

2.2 Delta机器人的位置正解

运动学正解即已知机器人各个运动关节的关节变量，求解机器人末端(动平台中心点)的位置。利用式(2)可以得到O'在O-xyz中的位置矢量x,y,z的方程组，该方程组有3个等式，3个未知量(x,y,z)，通过解方程组可以得到末端位置。但是，该方程组是非线性方程组，解析解不易求得，而且还存在多解问题，需要对解进行取舍。哈尔滨工业大学的赵杰[4]采用几何法，构造出特征四面体，求出它的唯一正解，如图2所示，分别将E1P1，E2P2，E3P3沿着P1O’、P2O’、P2O’平移，并交于O’点，设此时的E1，E2，E3分别移动到Q1，Q2，Q3点，由于Qi点的坐标已知，而O’到Qi点的距离始终等于l2，可据此列出方程，求出O’的位置坐标。

将图2中的三棱锥单独提出来分析，如图3所示，H为△Q1Q2Q3的外心，K为边Q1Q3的中点，容易证明O’H⊥△Q1Q2Q3，且H为垂足。

(5)

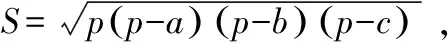
△Q1Q2Q3的外接圆半径：

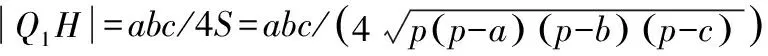
(6)

(7)

OO'=OH+HO'=OK+KH+HO'

(8)

式(8)就是运动学正解方程，已知θ1，θ2，θ3，l1，l2，R，r几个参数，代入式(5)、式(6)、式(7)、式(8)，即可以求出O’的坐标。

3 Delta机器人的工作空间

机器人的工作空间是机器人操作器的工作区域，它的大小是衡量机器人性能的重要指标[5]。影响并联机器人工作空间大小的因素主要有：1) 杆长的限制：当杆长达到极限时，动平台给定参考点也达到了工作空间的边界；2) 运动副转角的限制：球面副和转动副的转角在实际并联机器人产品上通常都有限制；3) 连杆的干涉：连杆在运动过程中可能会发生干涉。并联机器人的工作空间的解析求解是一个很复杂的问题，故采用数值积分法来计算工作空间的范围。

常用的工作空间的计算方法有几何法、离散化方法、数值方法等，这几种方法各有优缺点，在不同机构中所用的方法也不尽相同。

对于Delta机器人而言，选择动平台的中心点为参考点，则该点可以到达的点的集合即为Delta机器人的工作空间。Delta机器人结构相对简单，输入变量为主动臂的3个转角θ1，θ2，θ3，动平台在运动过程中始终保持与静平台平行(即保持水平)，所以不存在姿态角度的变化，在分析工作空间时，只要分析单一姿态下参考点所达点的集合。

式(8)为运动学的正解方程，它反映了输入量与参考点坐标与输入量之间的关系，通过给定合理的输入变量并代入该方程，即可得到参考点坐标，这些坐标点的集合就是Delta机器人的工作空间范围。

4 仿真

Delta机器人仿真使用的结构参数如下：静平台外接圆半径R=195mm，动平台外接圆半径r=65mm，主动臂杆长l1=200mm，从动臂l2=500mm。根据实际的结构，主动臂转角θi限制为20°～160°，通过给定具体数值，使用MATLAB编程，分别使θ1，θ2，θ3从20°～160°之间等间距取50个值，代入正解方程，生成可视化的工作空间仿真图形，如图4所示。

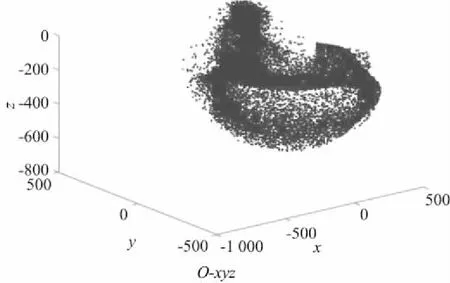
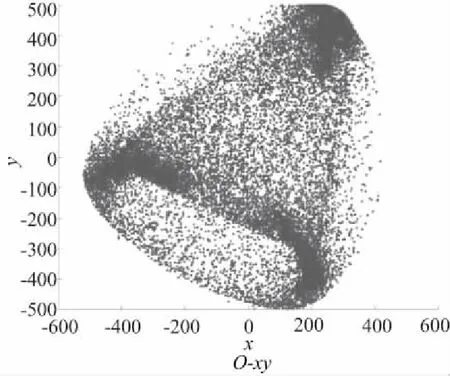
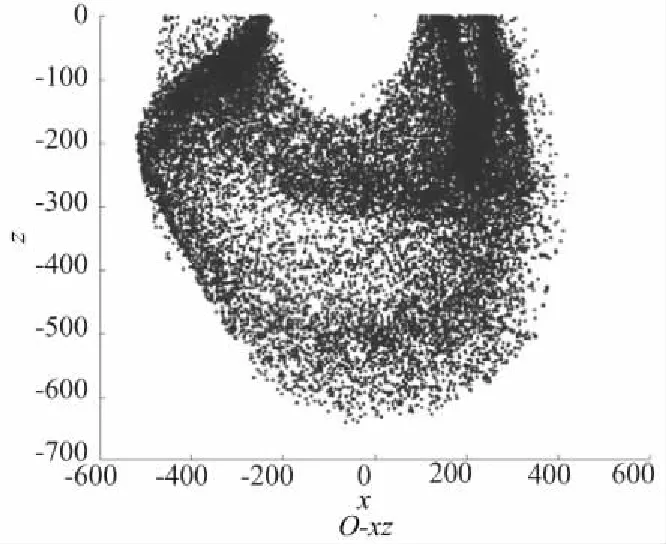
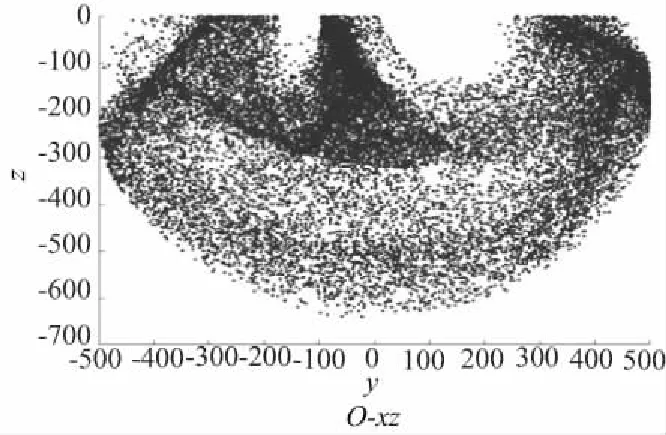
图4 工作空间仿真结果

从图4中可以清晰地看到Delta机器人的工作范围，Delta机器人的工作空间呈椭球型，且在靠近z=0平面时会有一段不可达的区间(空洞)，这段区域的大小是由主动臂杆长，从动臂杆长，动静平台尺寸共同决定的，通过合理设计各杆长，可以优化Delta机器人结构，使机器人有更大的工作范围。

5 结语

机器人工作空间的分析对于机械本体设计、轨迹规划

及控制系统设计都有重要的意义。本文通过对Delta结构的分析，根据Delta结构的特点建立了约束方程，并借此求出了运动学逆解，采用几何法求取运动学正解方程，并在运动学正解的基础上，借助MATLAB软件，得到了Delta机器人的可达工作空间，为衡量Delta机器人性能提供参考依据。

[1] J.-P., 梅莱,黄远灿. 并联机器人[M]. 北京：机械工业出版社, 2014.

[2] 梁香宁, 牛志刚. 三自由度Delta并联机器人运动学分析及工作空间求解[J]. 太原理工大学学报, 2008(1):93-96.

[3] 黄真, 刘婧芳, 李艳文. 150年机构自由度的通用公式问题[J]. 燕山大学学报, 2011(1):1-14.

[4] 赵杰, 朱延河, 蔡鹤皋. Delta型并联机器人运动学正解几何解法[J]. 哈尔滨工业大学学报, 2003(1):25-27.

[5] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京：高等教育出版社, 2014.