基于多目标不确定综合评测的宜居性研究——以淮海经济区为例

李昭君，洪桂云

(安徽建筑大学 环境与能源工程学院，安徽 合肥 230601)

关键字：模糊综合评价法；宜居城市；多指标不确定综合评判方法；期望值准则比较法

0 引言

随着社会的不断发展，人民追求生活质量，建设宜居城市成为政府完善城市功能的焦点。国外研究中的评价指标侧重考虑城市居民在大社会环境下的满意度，如2017年，Emilija Sofeska[1]提出城市是一个复杂的人造人工实体，宜居性由居民定义并改造城市达到可持续发展。国内的李丽萍、郭宝华在《关于宜居城市的理论探讨》[2]中提出宜居城市的七大判别标准——经济发展度、社会和谐度、文化丰厚度、居住舒适度、景观怡人度、公共安全度。

在宜居城市的评价体系中，指标易受到一些不确定因素的影响，如突发自然灾害、房价的大幅度波动、宏观的政策调整等，这些都在无形中对我们所筛选出的评价指标的相关数据产生影响，而这些因素具有不确定性，其影响程度也不同。因此，本文建立多目标不确定综合评测方法，对这些不确定因素进行分析，从而得出合理的不确定性因素评价宜居城市的数学模型。

1 宜居城市评价指标的筛选

根据《宜居城市科学评价标准》[3]中提到的宜居城市评价指标体系，具体内容整理见表1。

运用层次分析法[4]，分别比较一层的因素C1,C2...Cn对上一层因素O的影响，建立了1～5标度的矩阵判断标度如表2所示。

本文采用《宜居城市科学评价标准》的指标权重W，对其进行一致性检验，定义一致性指标C.I=通过一致性比率判断正互反矩阵是否通过一致性检验。当一致性比率C.R＜0.1时，认为判断矩阵的不一致性在容许范围内，即通过一致性检验，将权重大的指标选取出来，作为宜居城市判断的主要指标如图1。

图1 宜居城市评价指标及权重

表2 层次分析法矩阵判断标度

2 建立模糊综合评价模型

2.1 建立各级指标层

模糊综合评价的各级指标层如图2所示。

图2 宜居城市评价体系指标图

2.2 确定分解标准值

本文收集整理2011～2016年淮海经济区内8个城市(宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北)的数据[5-6]。具体的数据指标名称如表3的指标所示。将每项指标的数值从小到大进行排序，然后分别求出其极值。因为本文将宜居城市分为三个等级(宜居城市、较宜居城市、宜居预警城市)，因此结合五年内的数据分布，将其极值合理的分配到三个区间内。宜居城市指标体系分等级结果如表3所示。

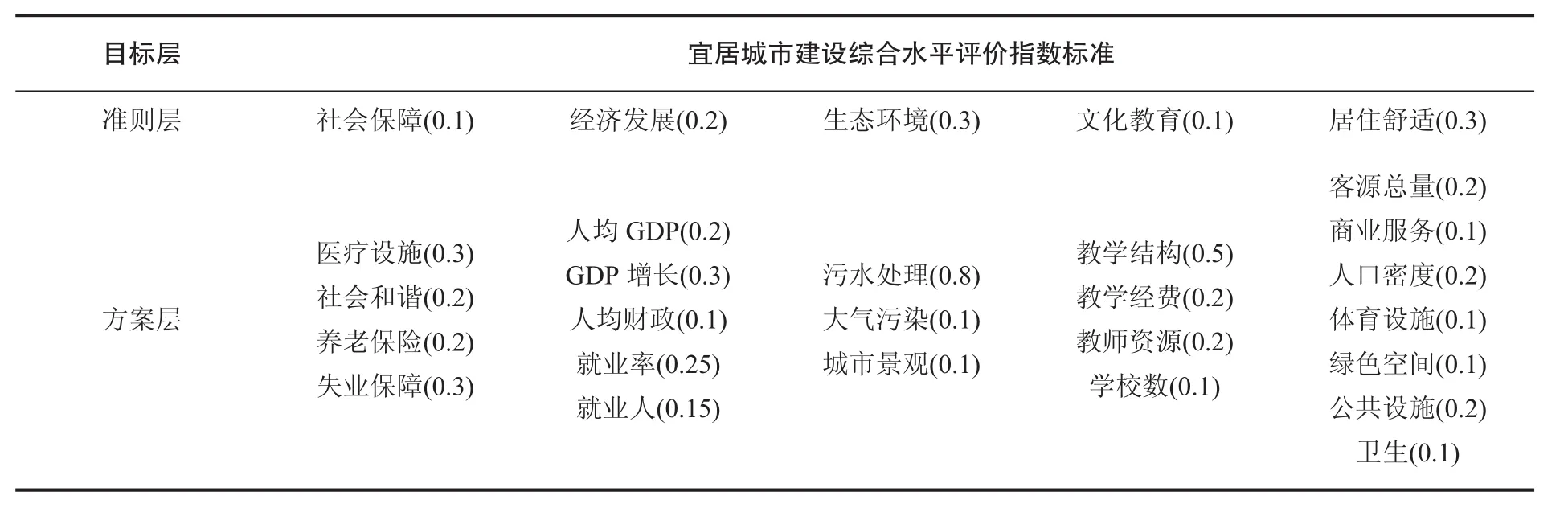
表1 宜居城市科学评价指标

2.3 建立评价因素集

综合评价淮海经济区内8个城市(宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北)，将图2中方案层作为评判的标准。将U表示为评判标准的集合，u1为人均GDP，依次类推。得到公式(1)因素集

2.4 建立评价等级集

设定评价等级集，将城市经过评判后的结果作为城市宜居的依据，等级集设定如(2):

式(2)中1、2、3分别表示宜居城市、较宜居城市和宜居预警城市。

2.5 建立评价矩阵R

参与评价的因素有12个，各个标准判定之后的等级分为3个等级。对U中每一个因素进行模糊综合分析。记rij表示第i中评判指标的第j个等级的可能性，即rij是i对j的隶属度，所以可以得到如下评判矩阵(3):

规定rij是i对j的隶属度，参考《基于改进隶属度函数的电能质量模糊综合评价》[7]隶属度函数公式，得到城市宜居指标隶属度函数公式(4)。

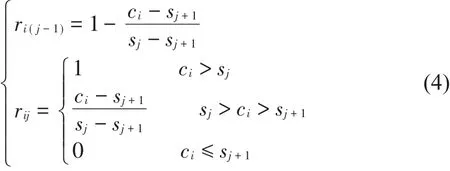
公式(4)中，ci是城市宜居性第i个评判标准，sj是第j个的分类标准边界值。8个城市的判断矩阵为Ri(i=1,2...8)，8个城市的排列顺序为宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北，R1表示第1个城市(宿迁)的判断矩阵。

2.6 确定权重W

由于影响一个城市的宜居城市的评判指标有很多，各个指标对城市的宜居性的影响也不会完全相同，因此对各个指标因素进行权重设定。用指标权重表示指标对城市宜居性评判的影响。

经过计算后得到各个评判标准的权重矩阵如公式(6)所示。

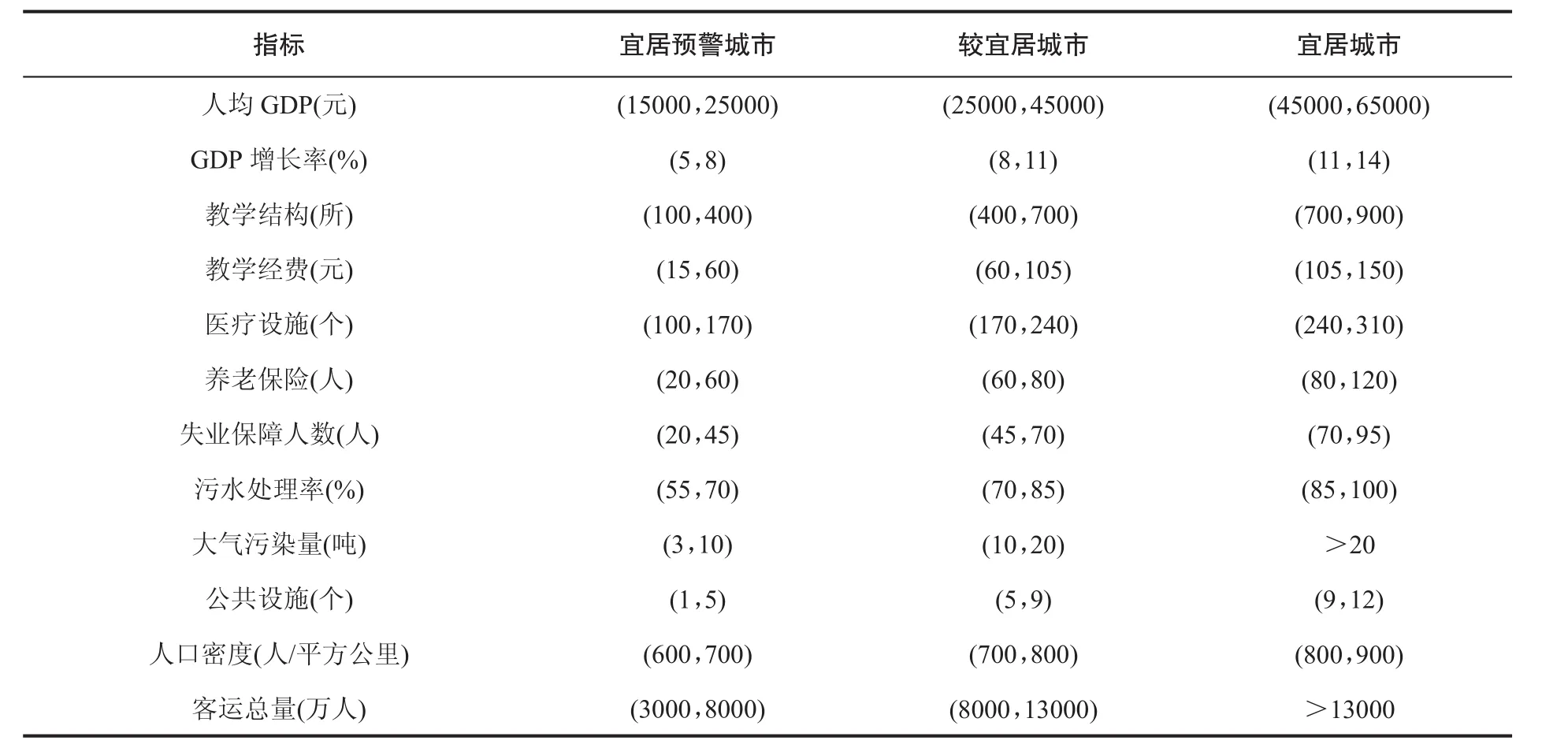
表3 宜居城市指标体系分等级表

2.7 加权后的评价矩阵

加权后的评价矩阵如式(7):

3 淮海经济区城市宜居性的综合评价

根据分解表3宜居城市指标体系分等级中的标准值，将各个城市的12项主要评价指标进行划分等级，求其在三个等级内的概率分配，得到表4徐州市宜居指标体系及宜居表所示(这里只列出徐州的整理数据为例)。将城市的12项评价指标按照表3等级标准值划分为三个等级，求得指标在等级内的概率分配。得到表4徐州市宜居指标体系及宜居表所示(这里只列出徐州的整理数据为例)。

3.1 求解权重向量

由于指标的矩阵经过了一致性验证，其权重具有可信度，故其一级指标的权重如公式(8)所示。

二级指标的权重如公式(9)所示。

各个子因子集进行一级模糊综合评价如公式(10)所示。

徐州市二级综合综合评价如公式(11)所示。

通过Matlab计算可以得到如下结果如公式(12)所示。

表4 徐州市宜居指标体系及宜居表

3.2 宜居城市综合评估排名

根据最大隶属度原则，认为徐州市的宜居程度为宜居城市，同理对淮海经济区内的其他7个城市进行评价。T值越大城市宜居性越好，根据隶属度最优原则，将公式(12)中算出的T的最大值进行排序，即为该评价体系下宜居城市的排名。8个城市宜居评价排名结果如表5所示。

4 基于不确定性因素评价宜居城市的数学模型

城市宜居性的评判是一个多属性、多指标的问题。在对其进行定性分析后，即经过主成分分析筛选得出12个评价指标:人均GDP、GDP增长率、教学结构、教学经费、医疗设施、养老保险、失业保障人数、污水处理率、大气污染率、公共设施、人口密度、客运总量。需要利用数学知识进行定量研究，这个过程往往存在一些非确定性因素，如:突发自然灾害、房价的大幅度波动、宏观的政策调整等。这些不确定因素对所筛选出的评价指标的相关数据产生影响，其影响程度也不同，对这些因素不同的处理方式产生不同的综合评判方法。

因此本文建立多目标不确定综合评测方法[8]，分析不确定的因素，得出合理的不确定性因素评价宜居城市的数学模型，结合利用模糊综合评价得出的排名结果，将每两个排名相邻的城市进行不确定性综合评测，得出基于不确定因素的新宜居城市排名。

表5 8个城市宜居评价排名结果

4.1 不确定理论预备知识

首先利用期望值准则比较法，建立不确定评价矩阵[9]。

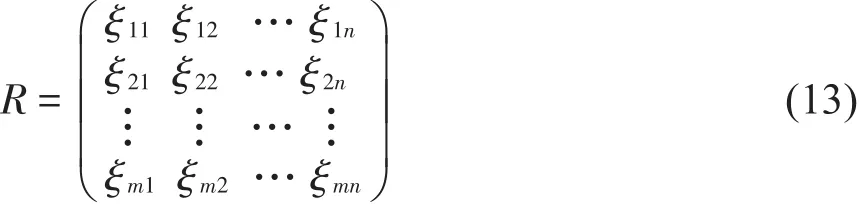
再用指标的权重W与公式(13)所示的矩阵R(13)相乘，得到新的向量B，如公式(14)所示。它的元素ξj( )

j=1,2,...,n代表标准化数据对评级对象的综合不确定评价。

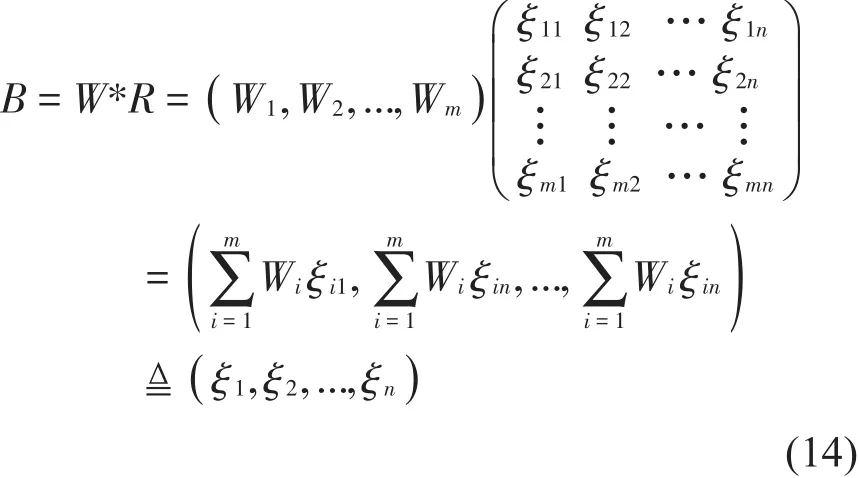
用向量B标准化后的数据的设置权重相乘，得到该评价对象的不确定综合评价，如公式(15)所示。不确定变量ξ，如公式(16所示)。

4.2 模型建立

4.2.1 建立评价指标体系

利用主成分分析得到的指标体系和权重，研究不确定因素如何对每项指标进行关联评价的问题。本文把不确定的因素当成不确定评价，建立不确定综合评价模型，提出不确定综合评价方法。注:指标之间都是互相独立。

4.2.2 建立不确定评价矩阵

我们用不确定变量ξ和η分别表示在第2问中的排名为1和2的徐州和商丘。

下面逐层进行不确定性评价，首先通过整理数据，对指标层(即方案层)的二级指标进行评价。

徐州:结合所统计得到的指标数据标准值[10]，模拟出作为其准则层一级指标A,B,C,D,E所对应的二级指标的不确定评价矩阵R1,R2,R3,R4,R5分别为:

4.2.3 数据标准化处理

由于各个数据的单位，数量级不同，所以将收集到的各项指标数据运用Matlab进行标准化处理。

4.3 模型求解

4.3.1 计算不确定综合评价指标期望值

根据评价数据计算准则层的5个一级指标的评价情况，即先把5个一级指标作为5个小目标。根据对应的二级指标的不确定评价情况，利用不确定综合评价方法解决5个小的评价问题，然后通过5个一级指标的评价情况计算出目标层宜居城市评价情况。首先把准则层的5个一级指标作为5个小目标，由评价数据计算其评价情况。其次利用不确定综合评价方法结合对应的二级指标不确定评价情况，解决5个小的评价问题。再由5个一级指标的评价情况计算出目标层宜居城市评价情况。根据定理4.1计算准则层一级指标的评价结果.

表6 不确定因素下宜居城市排名

同理可得

最后运用Matlab计算出徐州市的不确定综合评价结果为

同理，可以求得商丘市的评价矩阵，并计算5个一级指标对应的不确定性评价的期望值分别为

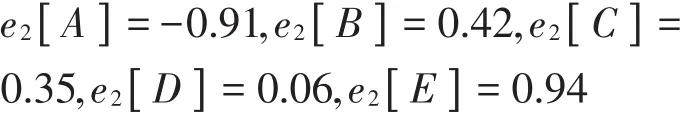
4.3.2 利用期望值比较得出结论

e由综合评价期望值比较准则可知，徐州市的宜居程度要优于商丘市的宜居程度。

结合上述方法，计算剩下的城市的不确定因素评价体系下的期望值准则，并进行比较，得到新的宜居城市评价排名如表6所示。

5 小结

基于不确定性因素评价宜居城市的数学模型结果表明徐州、济宁为较宜居城市，为人民选择定居城市提供有效的参考。在实际的宜居城市评判活动中，往往有些因素是非确定性的，不能进行严格的量化，或者有些指标缺乏大量的数据，很难准确地给出评判得分。而本文用不确定变量表示评价指标中的不确定因素，并将多个指标转化为单指标。再基于不确定理论提出多指标不确定综合评判方法，结合期望值法则，将受不确定因素影响的指标定量化，进一步完善宜居城市评价体系。