基于影响矩阵法的系杆拱桥索力调整分析

张文俊，胡 成

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引言

一般钢管混凝土系杆拱桥为外部静定、内部超静定结构，其集拱桥的跨越能力大和简支梁桥对地基适应能力强的优点于一身，因此大量应用于公路和市政桥梁中。对于具有刚性拱和刚性系梁的钢管混凝土系杆拱桥，其吊杆一般采用柔性吊杆，其张拉力对结构体系的内力分布有着很大的影响。对于确定的系杆拱桥结构体系，总能找到一组吊杆索力，使得结构在确定的荷载作用下，某种反映结构性能的指标达到最优[1]。钢管混凝土拱桥多采用先梁后拱的施工方法，吊杆一般采用两次张拉。吊杆初次张拉主要是为了保证结构在施工中的安全，二次张拉也称调索张拉是为了确保成桥状态时结构内力和线形趋近设计值。因此与初张拉相比，吊杆二次张拉精度要求更高，是施工控制的关键。在施工中采用何种有效的张拉工序，在确保张拉过程中结构安全的前提下，使得成桥时吊杆索力达到设计目标值是施工控制需要解决的关键问题。

目前在实际应用中，吊杆索力的调整方法主要有正装法、倒装法、影响矩阵法、无应力状态法等。正装法应用于吊杆索力调整时，需进行迭代计算，迭代次数多且收敛速度慢。倒装法由于索力调整时吊杆不能去除，不便于应用。无应力状态法应用于短索分析中采用锚头拔出量控制时误差较大，而将无应力索长控制转化为张拉力控制则张拉力与施工顺序有关，不能充分体现该方法的优点。对于对称结构，影响矩阵法可实现多根吊杆同时张拉，应用较为方便[2]。

本文采用影响矩阵法对某座在建的系杆拱桥的吊杆二次张拉问题进行了研究。基于归一化原理，给出了影响矩阵求解的简化方法，推导了吊杆张拉的千斤顶张拉力的计算公式，在此基础上，对吊杆张拉顺序及张拉过程中的索力变化规律进行了研究，确定了适合本工程的吊杆二次张拉工序，可为相关工程施工控制提供借鉴。

1 影响矩阵法原理及影响矩阵求解简化方法

1.1 影响矩阵法原理

影响矩阵法是以每根吊杆的张拉控制力为基本未知量，通过给吊杆施加单位力，利用有限元模型求出单位力作用下吊杆内力影响矩阵，建立典型方程，然后通过求解线性方程组得到每根吊杆的张拉控制力，从而使最终吊杆的张拉力达到规定的设计值[3]。

文献[1]指出，若结构满足线性叠加原理，则有:

其中，公式(1)中P0为索力调整前各吊杆的内力矩阵，T为各吊杆需要施加的索力增量，吊杆的张拉控制力为索力增量与其在张拉前的已有内力之和，Pm为各吊杆目标索力，A为索力影响矩阵。

式中:aij表示第j号吊杆施加单位力时对第i号吊杆内力影响量。

由公式(1)可得到吊杆内力增量为:

由分析可知，运用影响矩阵进行索力调整的关键在于索力影响矩阵的求解。目前求解影响矩阵法采用的方法主要有:修改总刚度矩阵法、基于强迫变形的影响矩阵法、基于结构连续变更定理生成影响矩阵法、基于归一化原理的影响矩阵法[4]。文献[5-7]采用修改总刚度矩阵法求解影响矩阵，该方法每去掉一组吊杆，需要重新计算结构的刚度，因而计算过程比较复杂。本文借助于有限元软件MIDAS/CIVIL，基于归一化原理，提出求解影响矩阵的实用的、简便计算方法。

1.2 基于归一化原理的影响矩阵求解

现以图1所示的一座简单的系杆拱桥为例，来具体说明采用基于归一化原理求解索力影响矩阵的主要思想。假设索力调整之前i号吊杆内力为T1，现将i号吊杆索力替换为T2，其余吊杆索力不作调整，在MIDAS/CIVIL有限元软件中建立一个仅考虑i号吊杆索力张拉到T2的施工阶段，进行施工阶段分析，可得到仅改变i号吊杆索力的情况下，其余吊杆的索力增量，然后将各吊杆索力增量乘以1(T2-T1 )作归一化处理，即可得到i号吊杆索力影响向量[8]。

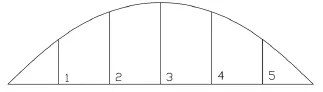
图1 系杆拱桥结构图

考虑吊杆组数为n的系杆拱桥吊杆索力调整张拉。不妨假设索力调整前吊杆张拉力向量为，目标索力值向量为借助有限元模型，按拟定的吊杆张拉顺序进行吊杆张拉的正装计算，其中每组吊杆的张拉值取为设计值。运行模型进行分析，可得到吊杆在各施工阶段的索力向量，记为:

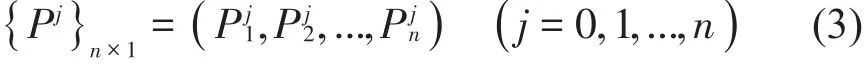
其中，公式(3)中j取0时表示吊杆索力调整前索力向量，表示第i组吊杆在j组吊杆张拉后吊杆索力向量。索力影响矩阵为:

其中，公式(4)中aij为第j组吊杆张拉时对第i组吊杆索力影响量。

具体的计算求解步骤:

步骤1:建立全桥有限元模型，将每组吊杆张拉设为一个单独的施工阶段，每组吊杆张拉控制力可取为设计值，按拟定的张拉顺序对各组吊杆进行张拉，对结构进行正装计算；

步骤3:按公式(4)求解索力影响矩阵，代入公式(2)即可得到各吊杆需要施加的索力增量T。

2 吊杆千斤顶张拉力的确定

按公式(2)求得的索力增量矩阵T仅为吊杆索力调整的增加值，并不能直接用于索力调整[9]。在索力调整过程中，后张拉的吊杆受先张拉的吊杆张拉影响索力值会发生变化，因而吊杆的千斤顶张拉力应计入先张拉的吊杆索力的影响量。

考虑一吊杆数为n的系杆拱桥，张拉顺序为1～n。张拉第1号吊杆，按照公式(1)，吊杆张拉前后索力值为:

其中，式中上标q和h分别表示吊杆张拉前和张拉后；P10为第1号吊杆初始索力，1号吊杆千斤顶张拉力为N1=Ph1=P10+T1。

张拉第i号吊杆，张拉前后吊杆力为:

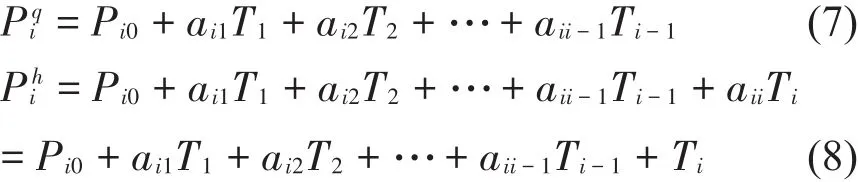
因此，i号吊杆千斤顶张拉力为:

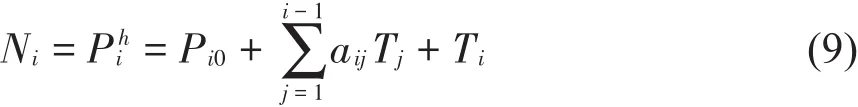
由公式(9)可知，i号吊杆的千斤顶张拉力由三部分组成:(1)初始索力值；(2)1～i-1号已张拉吊杆对i号吊杆索力的影响量；(3)索力增量。可见，虽然吊杆力增量与索力调整的顺序无关，但千斤顶张拉力会随施工顺序发生改变。由公式(1)可知，无论采用何种调索顺序，当所有吊杆张拉完成后，所有吊杆索力值将自动趋近设计目标值。

3 算例分析

3.1 工程概况

算例实桥为某下承式钢管混凝土系杆拱桥，计算跨径L=152 m，桥面采用钢-混凝土组合结构；拱轴线为悬链线，悬链线系数为1.5，矢跨比为1/4，矢高37.75 m；拱肋采用哑铃型钢管混凝土，单管直径120 cm，钢管壁厚1.8 cm，上下钢管中心距160 cm，全断面高300 cm，内充C50微膨胀混凝土。系杆采用箱形截面，系梁高200 cm，宽为160 cm；吊杆间距为7 m，每片拱肋设吊杆20根，吊杆采用PES7.0-73镀锌平行钢丝PE双护层拉索；全桥共设5道一字型风撑。

本桥采用先梁后拱的施工方法，主要施工步骤为:①搭设端横梁、系梁支架；②安装端横梁、系梁、横梁和小纵梁；③搭设拱肋支架，安装拱肋及风撑并灌注混凝土；④拆除拱支架，安装并第一次张拉吊杆；⑤对称、顺序安装预制桥面板；⑥拆除端横梁、系梁支架；⑦施工桥面铺装、防撞护栏等附属设施；⑧第二次调整吊杆力。

采用MIDAS/CIVIL建立全桥有限元模型，全桥总共分为1577个节点，2786个单元。吊杆采用桁架单元模拟，拱肋和系梁采用梁单元模拟。全桥有限元模型如图2所示。

3.2 吊杆千斤顶张拉力的求解

图2 有限元模型

全桥共20对吊杆，采用对称张拉，可简化为10组，从拱脚到拱顶由短到长依次编号为1-10。施工工序7完成后的索力值为初始索力值，初始索力值(本工程中初始索力值采用频率法测得)与设计成桥索力值见表1。拟定吊杆的张拉顺序为从拱顶向拱脚依次对称张拉，根据本文提供的简化方法进行索力调整分析，得到吊杆索力影响矩阵为:

在吊杆索力调整中，由于吊杆索力调整量与吊杆初始索力相比较小，调索过程中结构内力和位移一般不会控制张拉次序，因此理论上存在多种张拉方案使得在保证调索过程中结构安全的前提下，吊杆索力值达到设计目标值。本文考虑3种工程中常见的索力调整方案，对吊杆张拉过程中索力变化规律进行分析:

次序一:由拱顶向拱脚顺序、对称张拉，即:10-9-8-7-6-5-4-3-2-1；

次序二:由拱脚向拱顶顺序、对称张拉，即:1-2-3-4-5-6-7-8-9-10；

次序三:采用跳跃张拉的方式，张拉顺序为:10-7-4-1-9-6-3-8-5-2。

按公式(2)、(9)计算各组吊杆索力增量和千斤顶张拉力。将得到的千斤顶张拉力代入模型进行正装计算，得到三种次序下成桥状态理论成桥吊杆力，如表1所示。由表1可以看出，对于不同的张拉次序，尽管千斤顶张拉力不同，但成桥时各吊杆成桥索力值与设计值相比，误差均在1%范围内。对线弹性体，结构的最终状态与加载的顺序无关。因而，无论采用何种顺序进行索力调整，结构最终均能达到合理成桥状态。通过公式计算得到的千斤顶张拉力可直接根据油压表的标定曲线转化为油压表读数，直接用于指导桥梁施工。

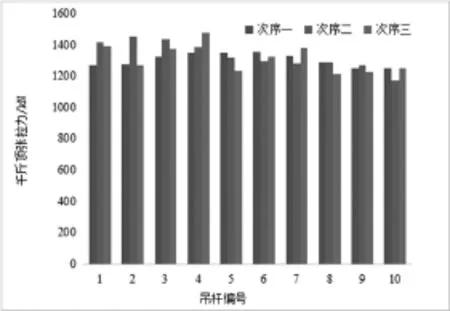
图3 不同张拉次序下千斤顶张拉力

由表1和图3可知，对同一组吊杆，采用不同张拉次序进行索力调整时时所要施加的千斤顶张拉力不同。不同张拉次序，千斤顶最大张拉力也有所不同。次序三千斤顶张拉力最大值出现在第4组吊杆，其值为1479 kN，次序二最大张拉力为第2组吊杆，其值为1454 kN，次序一最大张拉力为第6组吊杆，其值为1355 kN，次序一千斤顶最大张拉值比次序三小124 kN。在实际施工中，应寻求一组张拉力值较小的调索次序，这样既能保证结构局部受力安全，又能采用较小吨位千斤顶进行张拉，便于工程施工。因而采用次序一进行索力调整较优。

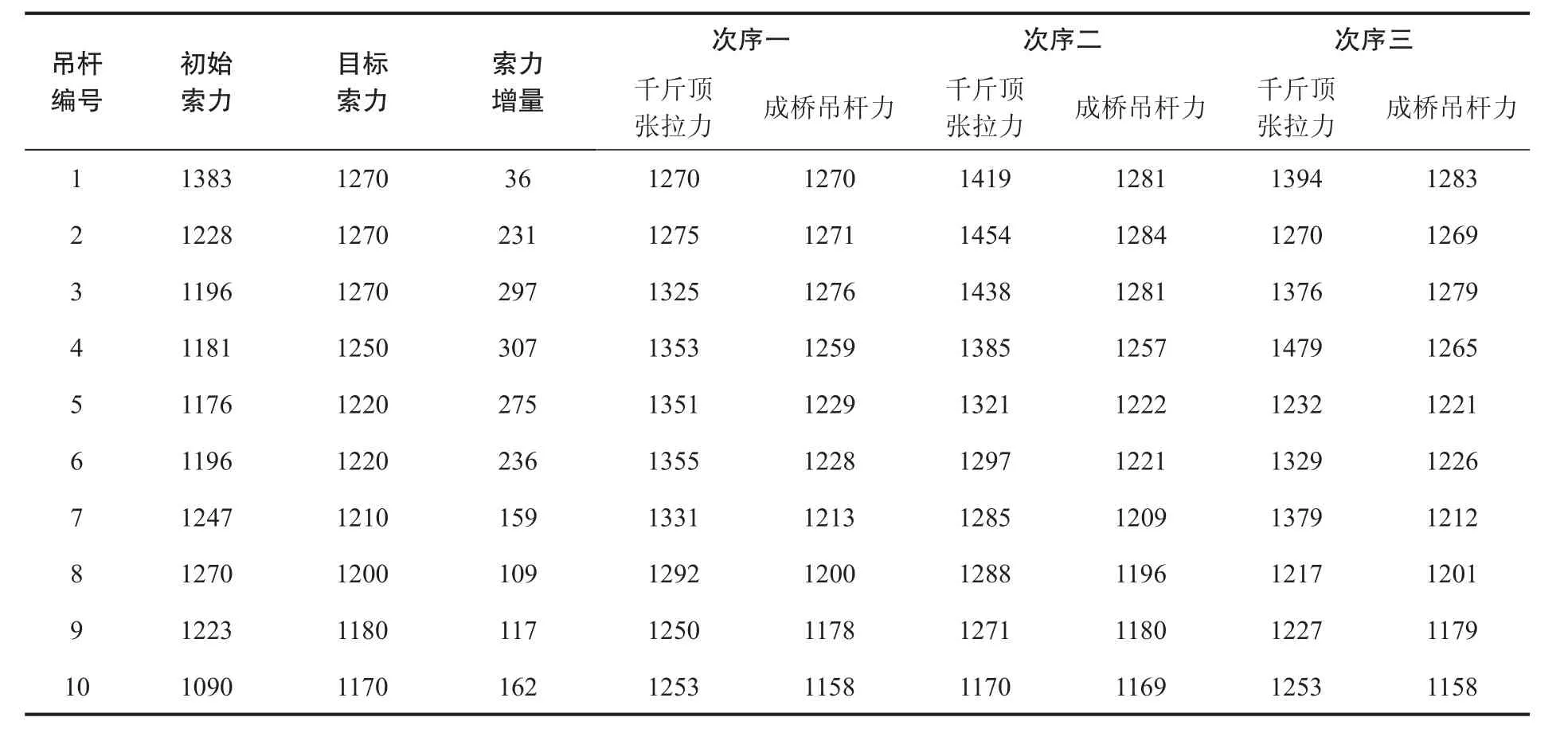
表1 不同张拉次序下吊杆千斤顶张拉力(单位：kN)

3.3 张拉过程中吊杆索力分析

考虑次序一的张拉顺序对吊杆索力进行调整，对张拉过程中的索力变化规律进行分析研究。调索过程中索力变化时程如图4所示。图中施工步骤1对应实际施工工序7，即桥面铺装完成，步骤2-11分别对应吊杆张拉10-9-…2-1。

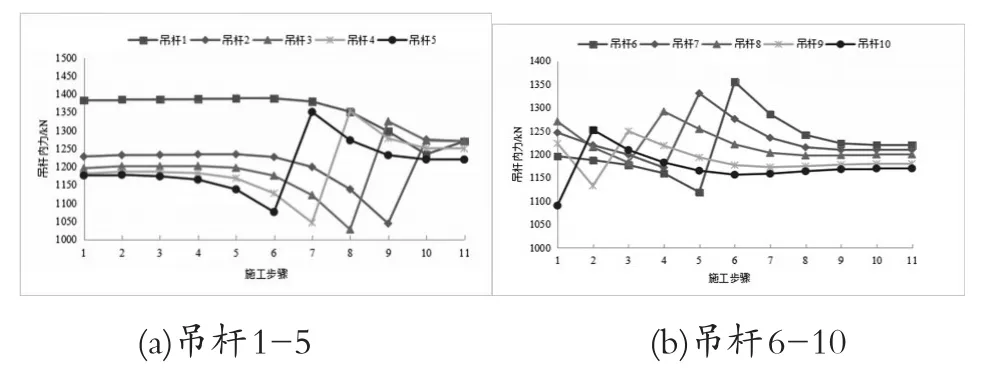
图4 索力变化时程图

由图4可以得出以下结论:

(1)吊杆的索力变化大致可分为三阶段:第一阶段为受前期吊杆张拉影响，索力减小，曲线呈下降趋势；第二阶段为受自身主动张拉，索力值明显增大，曲线呈明显上升；第三阶段为受后续吊杆张拉影响，索力值减小，曲线呈下降趋势。

(2)吊杆张拉时，对相邻吊杆的卸载作用明显，距张拉吊杆较远的吊杆受到的影响可忽略。靠近跨中的吊杆卸载作用影响范围大于靠近拱脚的吊杆。本工程中第7组吊杆张拉时(对应施工工序5)，对吊杆4-6、8-10内力值影响明显；第3组吊杆张拉时(对应施工工序9)，对吊杆1-2、4-5影响明显。

(3)由于相邻吊杆卸载作用，索力调整时施加的千斤顶张拉力要大于设计索力值。在拟定张拉顺序时，要考虑到实际工程中采用的千斤顶张拉吨位，确保确定的张拉索力在千斤顶张拉量程内。

(4)在张拉过程中，当某根吊杆索力超出千斤顶张拉吨位而无法进行直接张拉时，可利用相邻索力卸载作用，张拉其附近的吊杆使其索力值减小，从而可以进行下一步张拉。

4 结论

基于影响矩阵法，对系杆拱桥索力调整问题进行了研究。采用归一化方法，借助有限元计算提出了求解吊杆张拉索力影响矩阵的简便方法，并对索力调整中吊杆张拉力公式进行了推导。以某系杆拱桥索力调整为例，给出了三种索力调整方案并进行了比较分析。对调索过程中索力变化规律进行了研究，得到以下结论:

(1)吊杆张拉时，对相邻吊杆有明显卸载效应。靠近跨中的吊杆张拉时影响效应要大于靠近拱脚的吊杆。

(2)由于吊杆张拉时存在卸载效应，索力调整时一般需对要调整的索力值进行超张拉(张拉值大于设计值)。

(3)在拟定调索顺序时，要结合工程实际张拉时可用的千斤顶的吨位，确保吊杆最大索力在千斤顶张拉范围内，便于工程施工。

(4)在调索过程中，当某根吊杆索力值超出千斤顶的张拉范围时，可先张拉其附近的吊杆使其值减小，再对其进行索力调整。