直线与圆锥曲线的位置关系

江西省南昌市铁路第一中学 陈 辉

一、教学目标

1.知识与技能目标：能根据直线与圆的方程判断其位置关系，体会用代数方法处理几何问题的思想，能用数形结合的方法处理直线与圆的有关问题。

2.过程与方法目标：让学生在解决数学问题的过程中，体会到数形结合、转化、类比、归纳、猜想等数学思想方法。提高发现问题、分析问题、解决问题的能力。

3.情感、态度与价值观目标：让学生亲身经历知识生成的过程，体验探索的乐趣，增强学习兴趣；在“数”与“形”的对立与统一中，加强辩证唯物主义思想教育。

二、教学重点、难点

1.教学重点：（1）掌握直线与圆的位置关系的判定方法。

（2）运用数形结合和转化的思想方法，处理直线与圆的有关问题。

2.数学难点：“数”与“形”之间的转化技巧与方法。

三、学情分析及复习策略

对于解析几何，虽然每年花费大量的时间和精力进行复习训练，但解析几何的得分率都不高，原因是考生在学习解析几何时有畏惧心理,认为解析几何很难,考试时不敢做,放弃解析几何大题。

针对我们学生的实际情况，我在复习时主要让学生熟悉一些常见题目的解答模型，为学生做题指引思路方向，克服恐惧心理，再逐步提高难度、灵活性和综合性，从而提高得分率。

四、教学过程设计

（一）回归教材，整合要点

复习直线与圆锥曲线的位置关系、弦长公式、点差法、直线设法讨论。

（二）课前练习，夯实双基

若过原点的直线l与双曲线有两个不同交点，则直线l的斜率的取值范围是( )

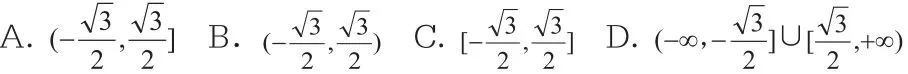
（三）例题讲解，授人以渔

题型一：弦长问题

例1 在直角坐标系xOy中，直线l：y=t（t≠0）交y轴于点M，交抛物线C：y2=2px（p＞0）于点P，M关于点P的对称点为N，连接ON并延长交C于点H，

又N为M关于点P的对称点，故

ON的方程为代入y2=2px整理得px2-2t2x=0，解得x1=0

设计意图：通过本题让学生充分体会弦长与坐标的相互转化关系。

题型二：对称问题

例2 试确定m的取值范围，使得椭圆上有不同两点关于直线l：y=4x+m对称。

解：设AB中点坐标(x0，y0)，由点差法得即y0=3x0，

又(x0，y0)∈l，y0=4x0+m，∴AB中点坐标（-m，-3m）。

∵中点（-m，-3m）在椭圆内部，

设计意图： 通过本题让学生充分体会如何将对称关系转化为代数关系。

题型三：面积问题

例3 如图所示，抛物线的顶点为O，点A(5,0)，倾斜角的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点，求△AMN的面积最大时直线l的方程，并求△AMN的最大面积。

解：设l：y=x+m,m

设M(x1，y1),N(x2，y2), 则x1+x2=4-2m，x1x2=m2。

∴△AMN的面积

从而

故直线l：y=x-1，△AMN的最大面积为

总结：将面积用底（弦长）和高（点到直线的距离）表示。

题型四：向量问题

解：设A(x1，y1),B(x2，y2)，M(0,2)。由

易知AB斜率存在，设AB：y=kx+2。

∴AB：

总结：将向量用坐标表示，结合x1+x2，x1x2消去x1、x2。

（四）课堂小结，提炼知识

（五）教学反思，查缺补漏

在教学中要重视基础，回归课本，先做比较基础的、典型的题型，然后逐渐提高难度，加入一些思维量比较大的题目，提高学生的分析能力及相关性质的灵活运用能力、计算整理能力，突破难点，克服恐惧心理。

（六）课后训练，巩固提高