基于锡组分和双轴张应力调控的临界带隙应变Ge1−xSnx能带特性与迁移率计算∗

底琳佳 戴显英 宋建军 苗东铭 赵天龙 吴淑静 郝跃

(西安电子科技大学微电子学院,宽带隙半导体技术国家重点学科实验室,西安 710071)

1 引 言

光电集成技术用CMOS工艺实现光子器件的集成制备,具有高集成度、高速率、低功耗的优势.目前,已有研究表明,锗(Ge)的锡(Sn)合金化可以实现能带结构的调控,在一定Sn组分条件下,Ge1−xSnx合金的直接带隙宽度会小于间接带隙宽度,实现间接带隙到直接带隙的转变,使Ge1−xSnx合金在光电探测、光电导器件、发光二极管、激光器等光电集成领域有更广泛的应用[1−5].

此外,Ge1−xSnx合金在金属-氧化物-半导体场效应晶体管(MOSFET)器件中也表现出高迁移率特性[6−8].然而,Ge中Sn的固溶度限制以及Ge和Sn的晶格失配,使Ge1−xSnx合金中Sn组分难以任意增大,并为Ge1−xSnx合金的制备带来了挑战[9,10].应变技术同样可以调控能带结构使Ge由间接带隙转变为直接带隙,其中以(001)面双轴张应变所需的应力最小,并且载流子迁移率,特别是空穴迁移率会显著增大[11−13].因此,考虑合金化和双轴张应力共同作用下的Ge材料,不仅可以有效减小直接带隙转变所需的Sn组分和应力,也可进一步提升Ge1−xSnx合金的光学、电学性质.

对双轴张应变Ge1−xSnx合金能带结构的研究是探索其光学、电学性质的理论基础.本文根据形变势理论分析了(001)面双轴张应力作用下Ge1−xSnx合金的带隙转变条件,给出了带隙转变临界状态下Sn组分和双轴张应力的关系;采用8k·p方法得到了临界带隙双轴张应变Ge1−xSnx在布里渊区中心点附近的能带结构,根据得到的能带图,由二阶函数拟合的方法得到了电子、空穴有效质量;基于载流子散射模型计算电子和空穴迁移率.相关结论可为高性能应变Ge1−xSnx电子器件和光电子器件的设计提供参考.

2 计算方法

2.1 形变势模型

在(001)面双轴张应力作用下,Ge1−xSnx合金的带隙类型和禁带宽度会随着Sn组分和应力而变化,其导带能谷能量可由形变势理论确定[11],导带Δ能谷因在(001)面双轴张应力作用下不会成为带边能级而未被考虑,

式中c11,c12为弹性劲度系数;σ为双轴应力,当σ＞0时为双轴张应力,σ＜0时为双轴压应力.

为了能够准确预测Ge1−xSnx合金能谷能量随Sn组分的变化情况,还需要用弯曲系数b对其进行二次修正[14],

式中x为Sn组分含量,EGe和ESn分别为Ge和Sn某一能谷能量,对于Γ,L能谷,相应的弯曲系数分别为−2.15和−0.91 eV.其他参数的取值以线性插值的形式给出,对于Ge和Sn,相应参数取值列于表1中[15].

表1 形变势模型所需参数取值Table 1.The parameter values of deformation potential model.

2.2 8k·p方法

应力作用下的金刚石型半导体,其哈密顿算符可简单表示为

式中Hk为k·p哈密顿量,Hε为应力引起的应变哈密顿量.对于直接带隙的Ge1−xSnx合金,由于导带、价带之间存在明显的耦合作用,为了得到准确的能带结构,由微扰理论和空间群对称性,可将Hk转换为一个8阶k·p矩阵,用来建立包含自旋轨道耦合在内的导带和价带能量色散关系,矩阵形式为[16,17]

其中

式中Δv为价带自旋轨道分裂能;Ec,Ev分别为未应变的导带和价带能量;ħ为约化普朗克常数;m0为电子有效质量;γ1,γ2,γ3为修正的Luttinger参数,它们与6k·p方法中Luttinger参数,的关系为,,其中Eg为带隙宽度,Ep为描述导带与价带耦合作用的Kane能量,与动量矩阵参数P0有关,.

(6)式中第二项Hε具有与(7)式类似的形式[16,17],

其中

式中av,bv,dv为价带形变势参数,j=x,y,z.

根据(6)—(8)式,通过对角化两个哈密顿矩阵的和可以得到应变Ge1−xSnx在布里渊区中心Γ点附近的能带结构.表2列出了计算所需参数的具体数值[18].

表2 应变Ge1−xSnx能带结构计算所需参数取值Table 2.The parameter values of energy band structure calculation for strained Ge1−xSnx.

2.3 载流子散射模型

载流子从状态k散射到状态k′的跃迁率Pk,k′可由费米黄金法则给出[19]:

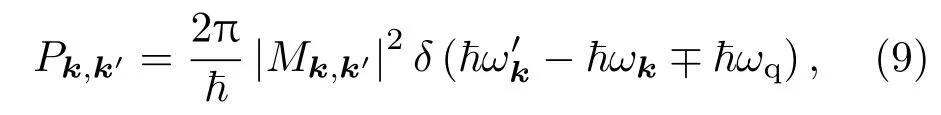
式中ħωk与分别为载流子初态和终态能量,ħωq为引起散射的量子能量,∓符号中“+”和“−”分别表示吸收或发射一个量子的能量,δ函数则表明在散射过程中能量守恒.Mk,k′为散射矩阵元,其形式为

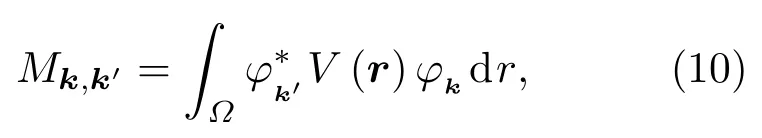
式中Ω为晶格体积,V(r)为散射势,φk为波函数.

任何改变晶格周期性势场的附加势都会引起载流子的散射[20].其中一类散射势,如晶格振动引起的各种散射势,表现为随时间t简谐变化的波的形式:

式中r,q分别为位矢和格波波矢,ωq为振动角频率,A+(q)与A−(q)互为复共轭.另一类散射势,如电离杂质的库仑势、混合晶体的无序势等,不随时间变化,傅里叶展开后具有如下形式:

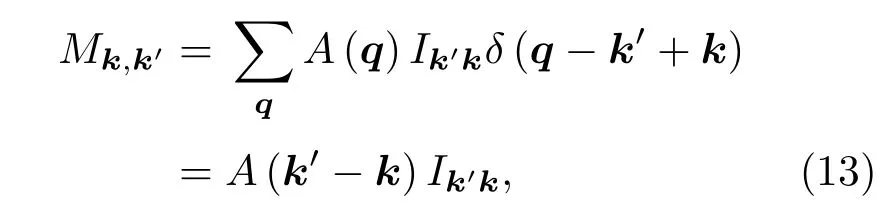
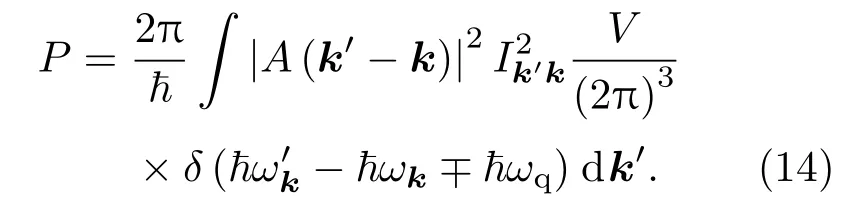
应变对载流子迁移率的影响体现在对电导有效质量和动量弛豫时间的调控中,但并没有改变载流子的散射机理.因此,在应变Ge1−xSnx合金中,导带Γ能谷存在离化杂质散射、声学声子散射以及合金无序散射,价带存在离化杂质散射、声学声子散射、非极性光学声子散射以及合金无序散射[21].

根据各散射机理的散射势,由(14)式可以分别建立离化杂质散射、声学声子散射、非极性光学声子散射以及合金无序散射的物理模型(分别用PII,Pac,Pop,Palloy表示)[19,22,23]:

式中Ni为离化杂质浓度,在计算中假设其为1017cm−3;m∗为态密度有效质量,e为自由电子的电荷量,ε0为真空介电常数,εr为相对介电常数,kB为玻尔兹曼常数,T为温度,Ξ为声学声子形变势,D0为非极性光学形变势,为纵向弹性常数,nop={exp[ħω0/(kBT)]−1}−1为平均光学声子数,ΔE为Ge与Sn的带隙差,N为单位体积内的原子数.由于Ge1−xSnx合金中Sn组分含量较小,因此Ξ和D0近似采用Ge的形变势值[24].对于导带Γ能谷,Ξ为7.5 eV;对于价带,Ξ和D0分别为3.5 eV和2.4×108eV/cm.其他参数的具体含义和数值见表3.

表3 Ge1−xSnx载流子散射概率计算所需参数取值Table 3.The parameter values for Ge1−xSnxcarrier scattering rate calculation.

根据电子和空穴的总散射概率Ptotal以及可计算得到应变Ge1−xSnx在Γ点处的电子、空穴迁移率,式中mc为电导有效质量.

3 结果与讨论

根据形变势理论,通过计算导带Γ与L能谷之间的能量差可以判断双轴张应变Ge1−xSnx的带隙类型.即当时,为间接带隙;反之,为直接带隙.图1所示为(001)面双轴张应力作用下,Ge1−xSnxΓ与L能谷能量差随应力和Sn组分的变化情况.由图可见,随着双轴张应力从0增加至2.45 GPa,Ge1−xSnx带隙特性转变所对应的Sn组分含量将由7.6%变为0,计算结果与文献[11,29]一致.若单独考虑合金化或双轴张应力作用,带隙类型转变需要较大的Sn组分或应力,这会给工艺实现带来诸多难题,而在合金化与双轴张应力共同作用的情况下,低Sn组分和应力的组合便可得到直接带隙Ge1−xSnx.在带隙类型转变的临界状态下,由可以得到Sn组分和双轴张应力近似呈线性关系:

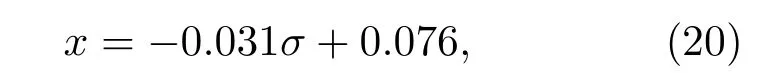
式中σ＞0,单位为GPa.基于这一临界条件,计算直接带隙Ge1−xSnx(称为临界带隙双轴张应变Ge1−xSnx)的电学性质,提出具有高载流子迁移率的Sn组分与双轴张应力的组合.

图1 (001)面双轴张应变Ge1−xSnxΓ与L能谷能量差等值线图(能量单位为eV)Fig.1.Contour plot of Ge1−xSnxbandgap difference betweenandfor biaxial tensile strain on the (001)plane.All energies are in eV.

图2所示为(001)面临界带隙双轴张应变Ge1−xSnxΓ点处的各能级偏移和禁带宽度随应力的变化情况,图中EcΓ,EV1,EV2,EV3分别表示导带带边能级、价带带边能级、价带亚带边能级和自旋分裂能级.由图2可见,由于双轴张应力的引入,价带带边和亚带边能级发生分裂,且分裂能随着应力的增大而增大,禁带宽度则随着应力的增大而减小.价带顶能级的分裂将改变带边和亚带边能级间的耦合作用,影响能带结构及有效质量.此外,空穴也会随着价带顶的分裂而重新排布,随着分裂能的不断增大,空穴越来越集中于价带带边能级,这有利于减小态密度有效质量和散射概率,提升空穴迁移率.

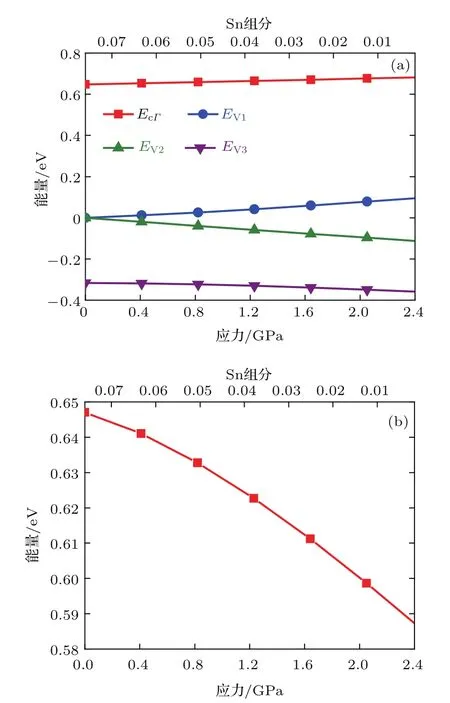
图2 (001)面临界带隙双轴张应变Ge1−xSnxΓ点处各能级偏移和禁带宽度 (a)能级偏移;(b)禁带宽度Fig.2. Energy level shift and bandgap of critical bandgap Ge1−xSnxat Γ for biaxial tensile strain on the(001)plane:(a)Energy level shift;(b)bandgap width.

为了探究双轴张应力对能带结构的影响,以(001)面临界带隙双轴张应变Ge0.96Sn0.04为例(应力约为1.16 GPa),给出其沿不同晶向的能带结构,如图3所示.从图3可以清楚地看到,双轴张应力引起的Γ点处价带简并的消除和晶体对称性的改变.

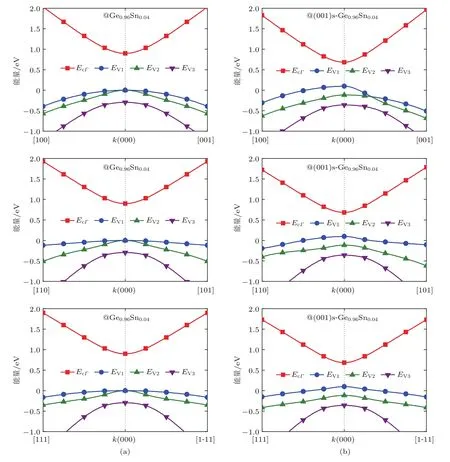
图3 Ge0.096Sn0.04沿典型晶向的能带结构 (a)未应变情况;(b)(001)面双轴张应变情况Fig.3.Energy band structure of critical bandgap Ge0.096Sn0.04along typical crystal orientations:(a)Unstrained Ge0.096Sn0.04;(b)biaxial tensile strained Ge0.096Sn0.04on the(001)plane.

图4所示为(001)面临界带隙双轴张应变Ge1−xSnx导带Γ能谷、价带带边能级和价带亚带边能级的40 meV三维等能图,其中Sn组分和双轴张应力的组合分别为7.6%-0 GPa,5.0%-0.84 GPa,4.0%-1.16 GPa,3.0%-1.48 GPa.等能面的曲率可以直观反映出有效质量的各向异性,特别是在(001)面双轴张应力作用下,各向异性更加显著.因此,在计算电子与空穴的输运特性时,为了获得准确的结果,必须考虑能带的各向异性.

图5所示为(001)面临界带隙双轴张应变Ge1−xSnxΓ能谷沿不同晶向的电子有效质量以及Γ能谷电子态密度有效质量和电导有效质量随应力的变化情况.由图5(a)可以看出,未受应力作用时,Ge1−xSnxΓ能谷是各向同性的,而在双轴张应力作用下,呈现明显的各向异性.这一点也可从等能图(图4(a))中得到印证:Γ能谷由原来的球形等能面转变为椭球等能面.因此,可采用类似于Δ和L能谷的计算方法来计算Γ能谷电子态密度有效质量和电导有效质量,如图5(b)所示.由图5(b)可见,Γ能谷电子态密度有效质量和电导有效质量随应力的增大而减小,这有利于增强电子输运特性.

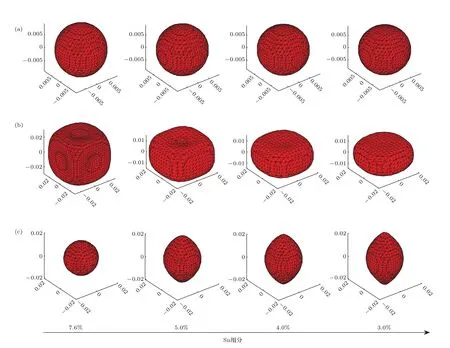
图4 (001)面临界带隙双轴张应变Ge1−xSnx(a)导带Γ能谷,(b)价带带边能级和(c)价带亚带边能级40 meV三维等能图Fig.4.Constant energy surface of critical bandgap Ge1−xSnxat 40 meV for biaxial tensile strain on the(001)plane:(a)Γ valley;(b)the fi rst valence band edge level;(c)the second valence band edge level.

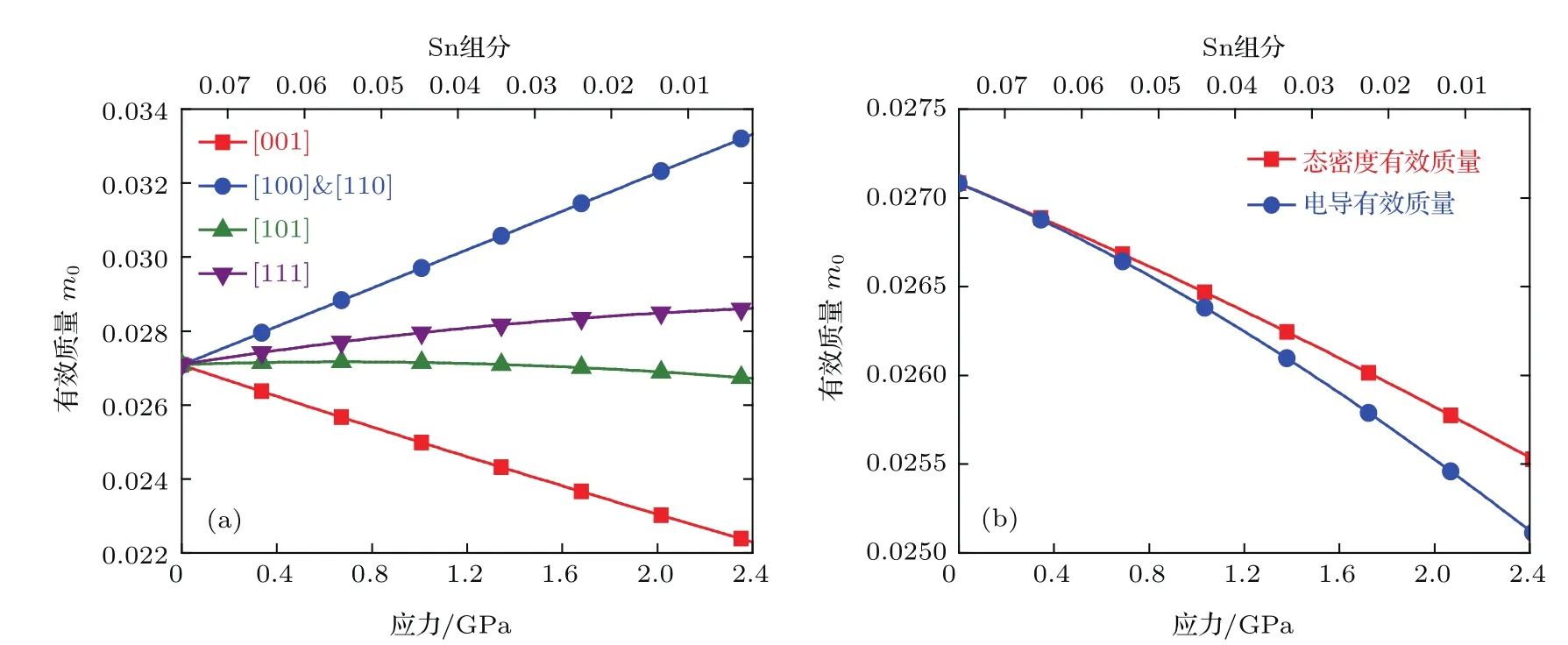
图5 (001)面临界带隙双轴张应变Ge1−xSnxΓ能谷电子有效质量 (a)沿典型晶向的电子有效质量;(b)电子态密度有效质量和电导有效质量Fig.5.Γ valley electron effective mass of critical bandgap Ge1−xSnxfor biaxial tensile strain on the(001)plane:(a)Electron effective mass along typical crystal orientations;(b)electron density of states and conductance effective masses.

图6所示为(001)面临界带隙双轴张应变Ge1−xSnxΓ点处不同晶向的价带带边能级和亚带边能级空穴有效质量随应力的变化情况.同样,双轴张应力也增强了空穴有效质量的各向异性.对于带边能级,沿不同晶向的空穴有效质量均显著减小并趋于平缓,其中以沿[001]晶向有效质量最低.对于亚带边能级,除[001]晶向空穴有效质量在应力作用下明显增大外,其他晶向空穴有效质量先增大后减小,但总体变化并不明显.空穴有效质量的显著减小归功于应力对晶格对称性的破坏,价带带边能级和亚带边能级的分裂改变了它们之间的耦合作用,使得能带发生翘曲,进而影响有效质量.

建立价带顶空穴态密度有效质量和电导有效质量,需要价带带边能级和亚带边能级的各向同性有效质量.因此,采用球形近似的方法[30],得到了(001)面临界带隙双轴张应变Ge1−xSnxΓ点处价带带边能级和亚带边能级的各向同性近似有效质量,如图7(a)所示.由图7(a)可见,在双轴应力的作用下,价带带边能级各向同性近似有效质量显著减小,而亚带边能级各向同性近似有效质量略有增大.此外,当双轴张应力增大到一定程度时,带边能级的各向同性近似有效质量已经小于亚带边能级,与弛豫状态相比,传统的重空穴、轻空穴的概念已失去意义.图7(b)所示为(001)面临界带隙双轴张应变Ge1−xSnx价带顶空穴态密度有效质量和电导有效质量,两种有效质量均随应力增大而显著减小,最终趋于平缓.可以看出,略大于1 GPa的双轴张应力足以得到较低的空穴态密度有效质量和电导有效质量,从而增强空穴输运特性.

图6 (001)面临界带隙双轴张应变Ge1−xSnxΓ点处价带各向异性空穴有效质量 (a)价带带边能级空穴有效质量;(b)价带亚带边能级空穴有效质量Fig.6.Hole anisotropic effective mass of critical bandgap Ge1−xSnxat Γ for biaxial tensile strain on the(001)plane:(a)Hole effective mass of the fi rst valence band edge level;(b)hole effective mass of the second valence band edge level.

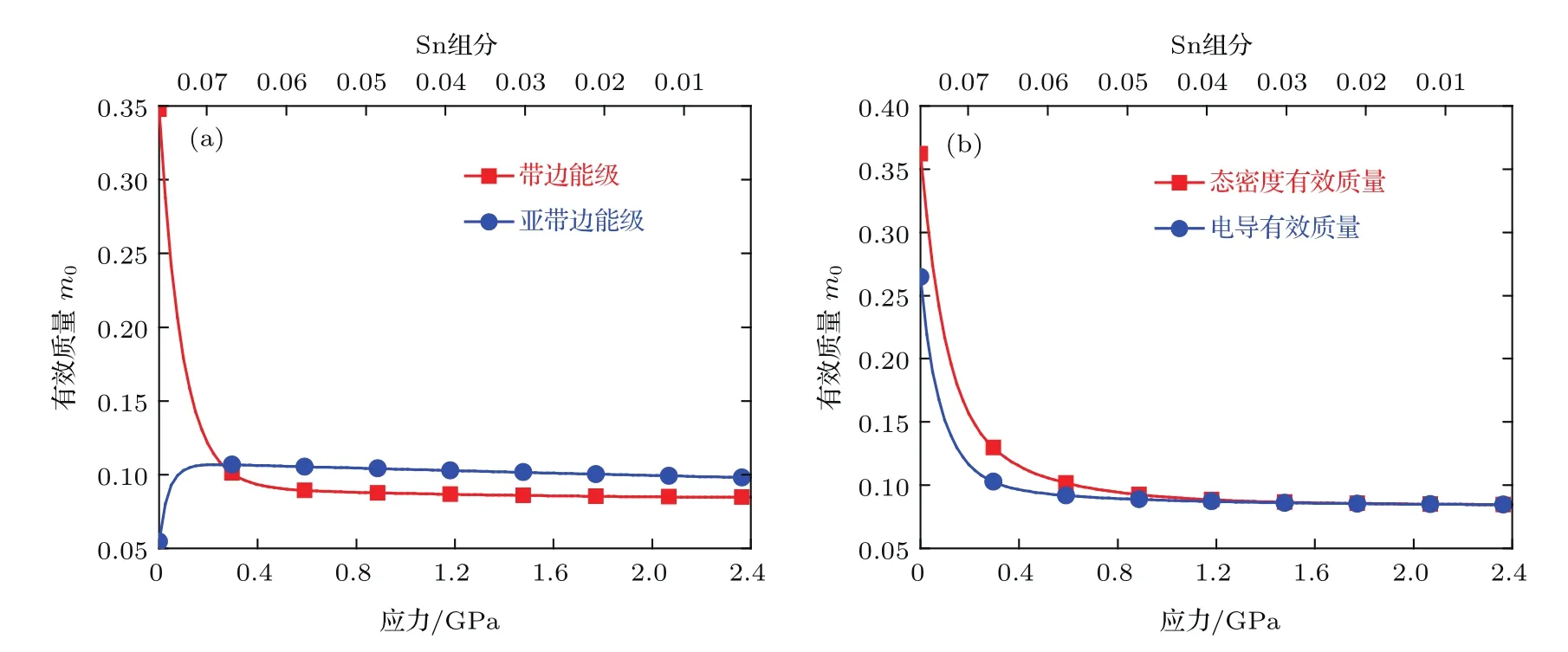
图7 (001)面临界带隙双轴张应变Ge1−xSnxΓ点处空穴各向同性近似有效质量、态密度有效质量和电导有效质量 (a)价带带边和亚带边能级各向同性近似有效质量;(b)空穴态密度有效质量和电导有效质量Fig.7.Hole isotropic approximate effective mass,density of states effective mass and conductance effective mass of critical bandgap Ge1−xSnxat Γ for biaxial tensile strain on the(001)plane:(a)Isotropic approximate effective mass;(b)density of states and conductance effective masses.

图8所示为(001)面临界带隙双轴张应变Ge1−xSnxΓ能谷电子离化杂质散射、声学声子散射、合金无序散射以及总散射概率随应力的变化情况.由于离化杂质散射处于主导地位,总的电子散射概率随着双轴张应力增大而增大,这是由于电子态密度有效质量的减小使得电子受到杂质中心散射的概率增大.

图8 (001)面临界带隙双轴张应变Ge1−xSnxΓ能谷电子散射概率 (a)离化杂质散射;(b)声学声子散射;(c)合金无序散射;(d)总散射Fig.8.Γ valley electron scattering rates of critical bandgap Ge1−xSnxfor biaxial tensile strain on the(001)plane:(a)Ionized impurity scattering;(b)acoustic phonon scattering;(c)alloy scattering;(d)total scattering.

图9所示为(001)面临界带隙双轴张应变Ge1−xSnxΓ点处空穴离化杂质散射、声学声子散射、非极性光学声子散射、合金无序散射以及总散射概率随应力的变化情况,除离化杂质散射外,其他散射的散射概率随双轴张应力增大而减小,显著降低了空穴总散射概率.相比于未应变情况,临界带隙双轴张应变Ge1−xSnx空穴迁移率将有较大幅度的提升.

图10所示为(001)面临界带隙双轴张应变Ge1−xSnx的电子和空穴平均迁移率随应力的变化情况.导带Γ能谷较小的有效质量使直接带隙的Ge1−xSnx合金具有非常高的电子迁移率,并且电子迁移率随着双轴张应力的增大而增大.空穴迁移率在较小的双轴张应力作用下即得到显著提升.因此,较小的(001)面双轴张应力不仅可以在低Sn组分下实现Ge1−xSnx合金由间接带隙到直接带隙的转变,而且通过对能带的改性增强了载流子迁移率.

将Ge1−xSnx合金生长在不同晶格常数的衬底材料上,可以实现Ge1−xSnx合金中双轴应力的引入.当Ge1−xSnx合金的晶格常数大于衬底材料时,会对Ge1−xSnx层引入压应力,当Ge1−xSnx合金的晶格常数小于衬底材料时,会对Ge1−xSnx层引入张应力.如文献[31]将Ge1−xSnx(Sn组分含量4.7%±0.4%)通过分子束外延的方法生长在应力弛豫的InyGa1−yAs缓冲层上,通过改变In组分的大小,对Ge1−xSnx层引入了−0.2%—0.88%的双轴应变量.根据本文计算结果,考虑工艺实现难度和材料性能两个方面,或可以选择4%Sn组分含量与1.2 GPa双轴张应力或3%Sn组分含量与1.5 GPa双轴张应力的组合来得到具有高载流子迁移率的直接带隙Ge1−xSnx合金.

此外,为了验证本文所得结果的准确性,表4对比了不同Sn组分和双轴应变组合下Ge1−xSnx直接带隙宽度的实验值与本文计算值.其中组合4已使Ge1−xSnx转变为直接带隙,这与本文计算所得的6%Sn组分和0.516 GPa(0.377%)双轴张应力的组合基本一致,间接说明了本文所得结果的准确性.

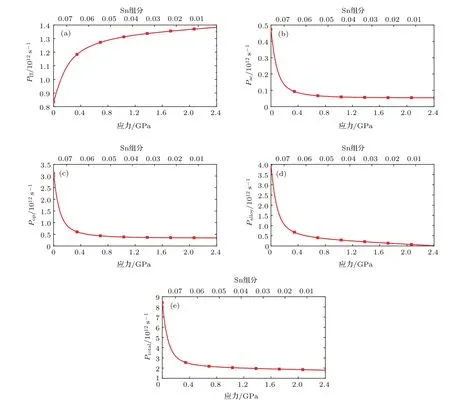
图9 (001)面临界带隙双轴张应变Ge1−xSnxΓ点处空穴散射概率 (a)离化杂质散射;(b)声学声子散射;(c)非极性光学声子散射;(d)合金无序散射;(e)总散射Fig.9.Hole scattering rates of critical bandgap Ge1−xSnxat Γ for biaxial tensile strain on the(001)plane:(a)Ionized impurity scattering;(b)acoustic phonon scattering;(c)non-polar optical phonon scattering;(d)alloy scattering;(e)total scattering.

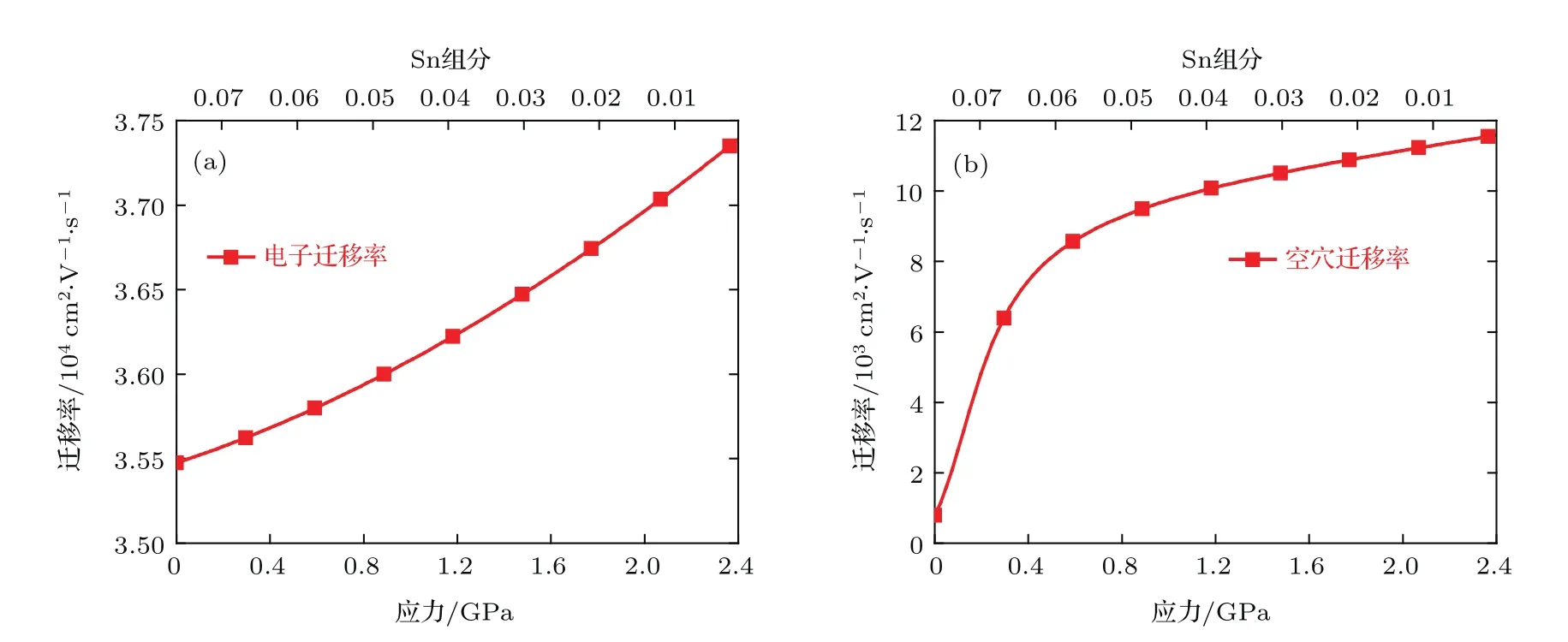
图10 (001)面临界带隙双轴张应变Ge1−xSnx载流子平均迁移率 (a)电子;(b)空穴Fig.10.Carrier mobility of critical bandgap Ge1−xSnxfor biaxial tensile strain on the(001)plane:(a)Electron;(b)hole.

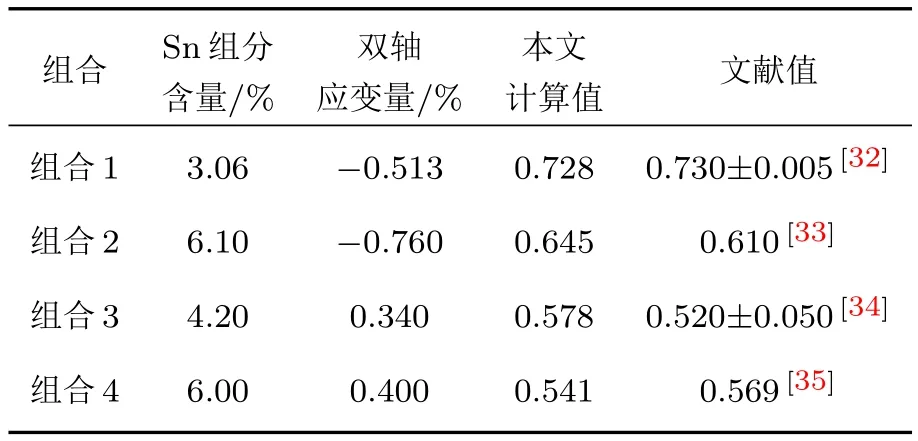
表4 本文计算值与文献实验值对比结果(300 K)Table 4.The comparison between the calculated values in this paper and the experimental values in literatures(at 300 K).

4 结 论

研究了Ge1−xSnx合金在(001)面双轴张应力作用下带隙特性和迁移率的变化情况.计算结果表明,在(001)面双轴张应力作用下,较小的Sn组分和双轴张应力的组合便可实现Ge1−xSnx带隙特性的转变,在临界状态下,Sn组分和双轴张应力近似呈线性关系x=−0.031σ+0.076.通过对(001)面临界带隙双轴张应变Ge1−xSnx能带结构的计算发现,Ge1−xSnx合金的直接带隙宽度受到双轴张应力的调制,会随着应力的增大而减小;直接带隙Ge1−xSnx合金较小的电子有效质量使其具有极高的电子迁移率,并且双轴张应力的作用有效降低了空穴有效质量和散射概率,使得空穴迁移率显著提升.考虑工艺实现难度和材料性能两个方面,可以选择4%Sn组分与1.2 GPa双轴张应力或3%Sn组分与1.5 GPa双轴张应力的组合用于高速器件和光电器件的设计.

[1]Morea M,Brendel C E,Zang K,Suh J,Fenrich C S,Huang Y C,Chung H,Huo Y,Kamins T I,Saraswat K C,Harris J S 2017Appl.Phys.Lett.110 091109

[2]Senaratne C L,Wallace P M,Gallagher J D,Sims P E,Kouvetakis J,Menéndez J 2016J.Appl.Phys.120 025701

[3]Hart J,Adam T,Kim Y,Huang Y C,Reznicek A,Hazbun R,Gupta J,Kolodzey J 2016J.Appl.Phys.119 093105

[4]Zhou Y,Dou W,Du W,Pham T,Ghetmiri S A,Al-Kabi S,Mosleh A,Alher M,Margetis J,Tolle J,Sun G,Soref R,Li B,Mortazavi M,Naseem H,Yu S Q 2016J.Appl.Phys.120 023102

[5]Wirths S,Geiger R,Driesch N V D,Mussler G,Stoica T,Mantl S,Ikonic Z,Luysberg M,Chiussi S,Hartmann J M,Sigg H,Faist J,Buca D,Grützmacher D 2015Nat.Photonics9 88

[6]Liu Y,Yan J,Wang H,Cheng B,Han G 2015Int.J.Thermophys.36 980

[7]Taoka N,Capellini G,Schlykow V,Montanari M,Zaumseil P,Nakatsuka O,Zaima S,Schroeder T 2017Mater.Sci.Semicond.Process.57 48

[8]Huang Y S,Tsou Y J,Huang C H,Huang C H,Lan H S,Liu C W,Huang Y C,Chung H,Chang C P,Chu S S,Kuppurao S 2017IEEE Trans.Electron Dev.64 2498

[9]Margetis J,Mosleh A,Al-Kabi S,Ghetmiri S A,Du W,Dou W,Benamara M,Li B,Mortazavi M,Naseem H A,Yu S Q,Tolle J 2017J.Cryst.Growth463 128

[10]Mosleh A,Alher M A,Cousar L C,Du W,Ghetmiri S A,Pham T,Grant J M,Sun G,Soref R A,Li B,Naseem H A,Yu S Q 2015Front.Mater.2 30

[11]Kurdi M E,Fishman G,Sauvage S,Boucaud P 2010J.Appl.Phys.107 013710

[12]Liu L,Zhang M,Hu L,Di Z,Zhao S J 2014J.Appl.Phys.116 113105

[13]Bai M,Xuan R X,Song J J,Zhang H M,Hu H Y,Shu B 2015Acta Phys.Sin.64 038501(in Chinese)[白敏,宣荣喜,宋建军,张鹤鸣,胡辉勇,舒斌 2015物理学报 64 038501]

[14]D’Costa V R,Cook C S,Birdwell A G,Littler C L,Canonico M,Zollner S,Kouvetakis J,Menéndez J 2006Phys.Rev.B73 125207

[15]Madelung O,Rössler U,Schulz M 2002Semiconductors·Group IV Elements,IV-IV and III-V Compounds.Part b-Electronic,Transport,Optical and Other Properties(Berlin:Springer)p2801,p3106

[16]Bahder T B 1990Phys.Rev.B41 11992

[17]Pryor C 1998Phys.Rev.B57 7190

[18]Zhu Y H,Xu Q,Fan W J,Wang J W 2010J.Appl.Phys.107 073108

[19]Ye L X 1997Monte Carlo Simulation of the Small-Scale Semiconductor Devices(Beijing:Science Press)p318,384(in Chinese)[叶良修 1997小尺寸半导体器件的蒙特卡罗模拟 (北京:科学出版社)第318页,第384页]

[20]Ye L X 2007Semiconductor Physics(2nd Ed.)Part One(Beijing:Higher Education Press)p203(in Chinese)[叶良修2007半导体物理学(第二版)上册(北京:高等教育出版社)第 203页]

[21]Sun Y,Thompson S E,Nishida T 2010Strain Effect in Semiconductors:Theory and Device Applications(New York:Springer)pp193–201

[22]Wang X Y,Zhang H M,Song J J,Ma J L,Wang G Y,An J H 2011Acta Phys.Sin.60 077205(in Chinese)[王晓艳,张鹤鸣,宋建军,马建立,王冠宇,安久华 2011物理学报60 077205]

[23]Song J J,Zhang H M,Hu H Y,Wang X Y,Wang G Y 2012Acta Phys.Sin.61 057304(in Chinese)[宋建军,张鹤鸣,胡辉勇,王晓艳,王冠宇2012物理学报61 057304]

[24]Nguyen P H,Hofmann K R 2003J.Appl.Phys.94 375

[25]Fischetti M V,Laux S E 1996J.Appl.Phys.80 2234

[26]Song P,Cai L C,Tao T J,Yuan S,Chen H,Huang J,Zhao X W,Wang X J 2016J.Appl.Phys.120 195101

[27]Myers V W 1967J.Phys.Chem.Solids28 2207

[28]Adachi S 2009Properties of Semiconductor Alloys:Group-IV,III-V and II-VI Semiconductors(Chichester:John Wiley&Sons Ltd.)p18

[29]Chen R,Lin H,Huo Y,Hitzman C,Kamins T I,Harris J S 2011Appl.Phys.Lett.99 181125

[30]Dai X Y,Yang C,Song J J,Zhang H M,Hao Y,Zheng R C 2012Acta Phys.Sin.61 237102(in Chinese)[戴显英,杨程,宋建军,张鹤鸣,郝跃,郑若川2012物理学报61 237102]

[31]Lin H,Chen R,Huo Y,Kamins T I,Harris J S 2011Appl.Phys.Lett.98 261917

[32]Lin H,Chen R,Lu W,Huo Y,Kamins T I,Harris J S 2012Appl.Phys.Lett.100 102109

[33]Gassenq A,Milord L,Aubin J,Guilloy K,Tardif S,Pauc N,Rothman J,Chelnokov A,Hartmann J M,Reboud V,Calvo V 2016Appl.Phys.Lett.109 242107

[34]Lieten R R,Seo J W,Decoster S,Vantomme A,Peters S,Bustillo K C,Haller E E,Menghini M,Locquet J P 2013Appl.Phys.Lett.102 052106

[35]Wirths S,Stange D,Pampillón M A,Tiedemann A T,Mussler G,Fox A,Breuer U,Baert B,Andrés E S,Nguyen N D,Hartmann J M,Ikonic Z,Mantl S,Buca D 2015ACS Appl.Mater.Interfaces7 62