聚噻吩单链量子热输运的第一性原理研究∗

吴宇蔡绍洪邓明森3)4)孙光宇2)刘文江

1)(贵州大学大数据与信息工程学院,贵阳 550025)

2)(贵州师范学院物理与电子科学学院,应用物理研究所,贵阳 550018)

3)(贵州师范学院,贵州省纳米材料模拟与计算重点实验室,贵阳 550018)

4)(贵州财经大学,贵州省经济系统仿真重点实验室,贵阳 550025)

1 引 言

有机导电材料聚噻吩自问世以来,以奇异的电学和光学性质吸引了众多研究人员的关注.2000年,诺贝尔化学奖授予艾伦·黑格、艾伦·麦克德尔米德和白川英树,以表彰他们在有机导电材料研究领域中的开创性贡献.2014年,世界上最小的发光二极管由聚噻吩单分子链实现,该材料的神奇用途得以展示[1],另外,在太阳能电池研究领域也能见到聚噻吩活跃的身影[2].

聚噻吩块体通常被看作绝热材料,热导率低于1 W·m−1·K−1,其绝热性由块体内部高分子链的形变和大量界面状态导致.事实上,沿聚噻吩分子链方向排列的无定形聚噻吩纳米纤维,室温下热导率高达4.4 W·m−1·K−1,高于聚噻吩块体的热导率[3].这种奇特的微观热输运机理值得探索.此外,聚噻吩作为热电材料也受到人们的青睐[4].根据ZT=S2GT/(Kph+Ke)[5],其中ZT为热电优值,表征材料的热电转换效率,S为材料的塞贝克系数,T为绝对温度,G为电导,Kph为声子热导,Ke为电子热导,由于本征聚噻吩单链的能隙约为2.0—2.3 eV[6],故Ke可忽略不计.探讨同位素掺杂对聚噻吩单链声子热导Kph的抑制效果,提高聚噻吩材料的热电转换效率,也是一个颇具价值的问题.这些都与聚噻吩单链的热输运性质紧密相关.我们希望确定纯聚噻吩单链热导率的理论上限,这在实验上难以实现,因为微观上存在诸多复杂且难以控制的因素.其次,同位素杂质是影响材料热输运性质的重要因素.石墨烯的热输运及其同位素效应在理论[7−12]和实验方面都有了较为深入的研究.温度约为室温时,12C石墨烯带中掺入一半13C原子后,热导率几乎降低一半[13].室温下,将自然丰度BN纳米管(19.9%10B,80.1%11B)中的11B含量提升至99.5%后,热导率提高了近一倍[14].

对于另一种有机高分子聚合物——聚乙烯,其出色的导热性能在实验和第一性原理角度已有研究[15,16].而聚噻吩单链量子热输运目前的理论研究仅限于分子动力学(MD)方法[3,17].为了体现该微观输运现象的量子特征,从量子力学出发,同时可有效避免MD中计算方法或经验势函数不同所导致的计算结果差异.鉴于聚噻吩在有机发光器件、太阳能电池、热电材料等方面的广泛用途,研究聚噻吩单链的量子热输运及其同位素效应,对认识聚噻吩的导热潜力以及调控其热性能十分必要.本文在密度泛函理论(DFT)计算基础上,用中间插入延展(CIS)[18,19]方法结合非平衡格林函数(NEGF)[20,21]方法,考察纯聚噻吩单链在室温下热导率的理论上限,以及一般掺杂比例下的热导同位素效应.

2 计算模型与方法

计算模型中,散射区域包含32个聚噻吩单胞,共计448个原子,总长度L=25.107 nm,两端分别为半无限长聚噻吩单链热极.纳米尺度下,声子的弹性输运占主导因素,若忽略声子间以及电、声子间的相互作用,且考虑特定掺杂比例下同位素杂质随机构型不同引起的透射系数平均效应,Landauer公式[12,22,23]给出的平均热导Kph为

式中ħ为约化普朗克常数,ω为声子频率,kB为玻尔兹曼常数,T为体系的绝对温度,Tph(ω)为声子透射系数,

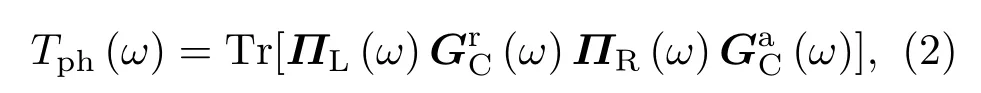
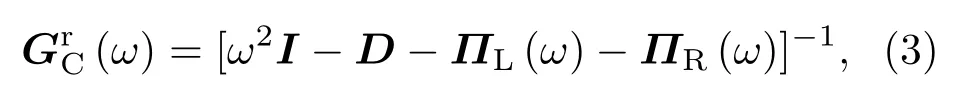
式中I为单位矩阵,D为散射区域的动力学矩阵:

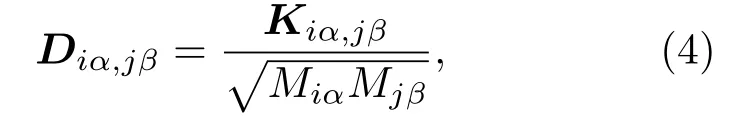
式中M为原子质量,力常数二阶张量Kiα,jβ的定义为

式中i,j为原子编号,α,β={x,y,z}表示三个正交方向,E为微观体系的总能量,R0为体系能量最低状态下的稳定几何构型,Qiα是第i个原子α方向的小位移量,F是原子间的相互作用力.

图1 含随机同位素杂质13C的聚噻吩单链示意图Fig.1.Illustration of a polythiophene chain containing random con fi guration of13C isotopes.

为了体现同位素随机掺杂后透射系数的统计平均效应,对每一种确定的同位素掺杂比例(100%掺杂的情形除外,此时物质为纯聚噻吩单链,没有随机因素,体系的平均透射系数与透射系数相同,平均热导与热导相同)计算10个随机同位素杂质构型,逐一计算各随机构型下的透射系数,再求其算术平均值,进而获得该掺杂比例下的平均透射系数〈Tph(ω)〉以及平均热导Kph.

聚噻吩单链的优化和力常数二阶张量的计算采用量子化学软件Gaussian09.计算选用杂化密度泛函b3lyp及6-31g(d)基组,优化后沿聚噻吩单链的方向单胞的晶格常数为7.846 Å(1 Å=0.1 nm),与X射线衍射(XRD)实验[24]测得的聚噻吩薄膜的晶格常数7.56 Å相近.构建的超胞包含3个聚噻吩单胞,在周期性边界条件下进行优化后,可得到聚噻吩单链的稳定几何结构,此时各原子的最大受力数值都低于10−3eV/Å,在此基础上,计算相应的力常数张量,并使最终得到的力常数张量与原物理体系的对称性一致[25,26].

在DFT计算获取超胞力常数张量的前提下,通过CIS方法进一步构造了25.107 nm长的聚噻吩单链的动力学矩阵.鉴于DFT计算与实验结果的差异,最终的声子透射谱经过计算化学比较和基准数据库(CCCBDB)的频率校正,校正因子取为0.960[27].CIS方法是一种电子结构线性标度算法,在计算大型准周期电子体系结构和量子输运中已得到严格验证和广泛应用[28−30].利用CIS方法扩展体系的力常数张量,极大地提高了计算效率,可以处理长达25.107 nm的聚噻吩单链及其同位素掺杂的声子散射问题.采用CIS方法得到的纯12C,32S聚噻吩单链的声子透射谱和热导,与直接用超胞力常数张量计算的结果完全相同,这印证了CIS方法计算结果的正确性.

声子在传播过程中与同位素杂质发生散射,使体系热导减小.纳米体系中,若直接用第一性原理方法计算包含数百原子体系的力常数张量,计算量极为巨大.作为简化处理,讨论声子与杂质散射常见的方法有级联散射模型[31,32]和标度理论方法[33,34].二者假定在低掺杂浓度下,杂质对声子的散射总效应可看作一系列相继单道散射效果的叠加,但这一假设对同位素杂质浓度(原子百分数,下同)高于10%的情况并不成立[12,31].用CIS方法在保持第一性原理精度的条件下大大提高了计算效率,因而可以采用直接模拟同位素杂质随机分布的办法,对包含448个原子的聚噻吩单链在各同位素掺杂比例下的平均热导进行研究.该方法可体现单、多道声子散射效应同时存在的一般情形,理论上能比较准确完整地描述一般同位素掺杂比例情况下的平均热导变化.

C的稳定同位素有12C,13C两种,其中12C的丰度为98.93%;S的稳定同位素有32S,33S,34S,36S,其中32S的丰度为94.99%.根据聚噻吩C,S原子的自然丰度,研究没有同位素杂质时纯聚噻吩体系的热导,即先考查纯净聚噻吩单链在以12C,32S作为基本组分时的热输运规律,再研究单独掺入13C,36S杂质时热导的同位素效应,最后讨论聚噻吩单链热导的原子质量效应.

3 结果与讨论

图2中纯净12C,32S聚噻吩单链声子的透射谱呈明显的量子化特征,热导量子化的基本单元为[35](h为普朗克常数),从第一个显著的量子化台阶可以看出,体系在低频极限时透射系数Tph=3.图2中最高声子频率在1500 cm−1左右,该频段对应C—C键伸缩振动,这与聚噻吩薄膜晶体拉曼光谱的测量结果一致[36].

为了考察不同频率的声子对热导的贡献,以图2中纯净12C,32S聚噻吩单链声子的透射谱为例,将(1)式的被积函数在T=300 K时作无量纲化处理,除以其在积分区间内的最大值,得到不同频率声子对热导贡献的相对强度r(ω).由图3可知,低频段声子的透射能力对体系的热导有决定性的贡献.

图2 100%12C和25%13C同位素掺杂的平均透射谱Fig.2.Average transmittance of pure12C sample and sample with13C isotope concentration of 25%.

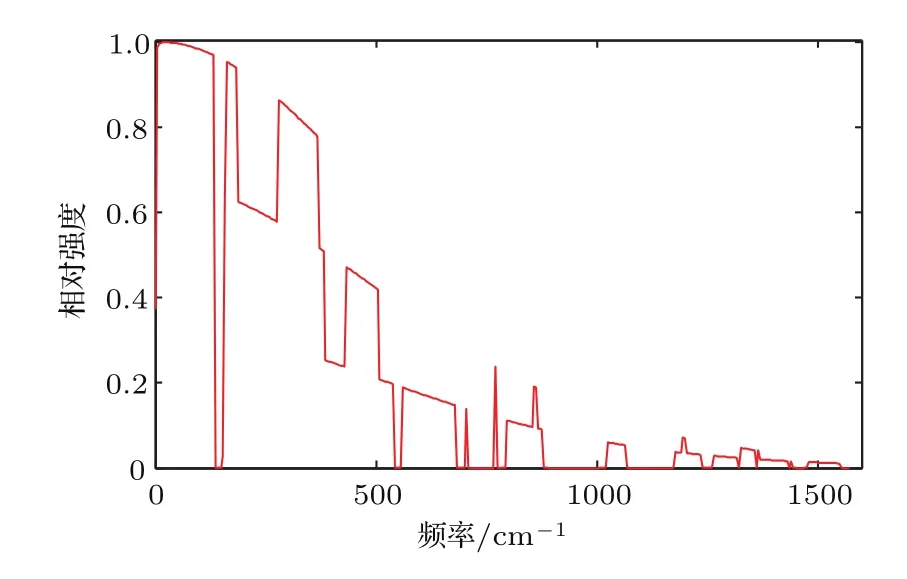
图3 T=300 K时不同频率声子对热导贡献的相对强度Fig.3.Relative intensity of a phonon contributing to the thermal conductance at different frequencies at 300 K.

如图4所示,继续提高13C原子的掺杂浓度,当C原子全为13C时,体系重新成为纯净的聚噻吩单链,此时透射谱再次呈现整齐的台阶特征,这说明同位素杂质概念的相对性.该透射谱形状与纯净12C聚噻吩的透射谱非常相似,只是整个透射谱向低频方向移动,截止频率从1550 cm−1减少到1500 cm−1,相应的C—C键振动频率降低.

从图5可以看出,随着温度的升高,体系的平均热导单调增加.对于12C聚噻吩单链,随着13C掺杂浓度由低到高,体系的平均热导先减小后变大,其中13C掺杂浓度为25%与75%时两条曲线基本重合.纯12C聚噻吩单链的热导比纯13C的聚噻吩单链略大.其他条件一定,聚噻吩单链中12C,13C原子等比例掺杂时,平均热导总是最小.

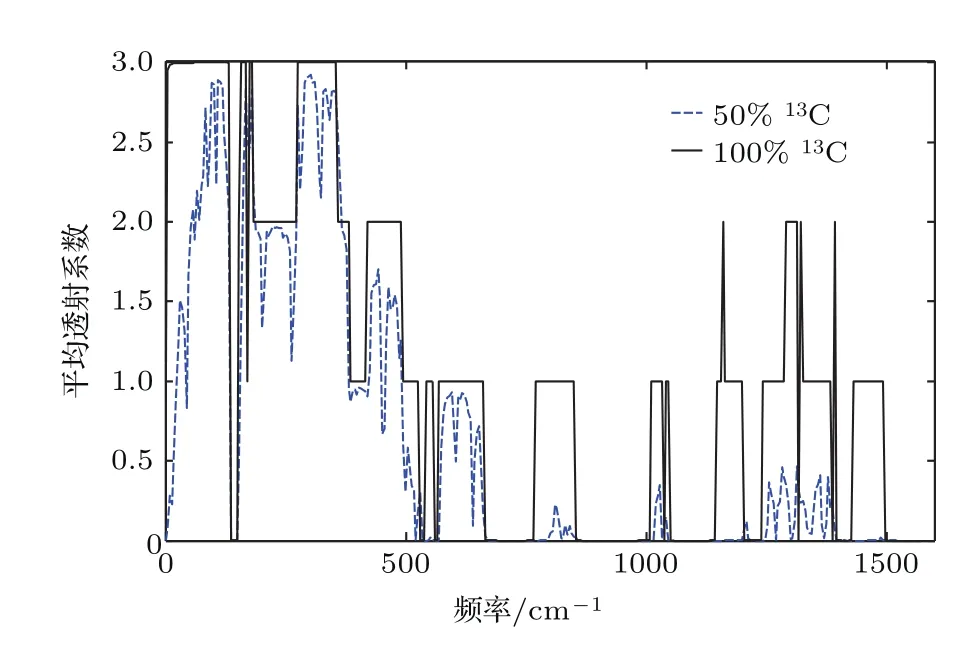
图4 50%13C同位素掺杂和100%13C的平均透射谱Fig.4.Average transmittance of samples with13C isotope concentrations of 50%and 100%.

图5 聚噻吩单链各同位素掺杂比例下的平均热导温度曲线Fig.5.Average thermal conductance versus temperature for different isotopic compositions.

考虑由12C,32S组成的纯净聚噻吩单链的热导率.在声子平均自由程以内弹性输运条件下,聚噻吩单链的热导率σ与散射区域的长度L成正比,σ=KphL/A[16],其中A为聚噻吩单链的横截面积.根据聚噻吩晶体薄膜X射线衍射实验的结果[24],用聚噻吩晶体薄膜的晶格常数a=10.80 Å,b=4.74 Å的乘积来定义横截面积.实验测定聚噻吩单链中的声子平均自由程非常困难[3].从实验结果来看,沿聚噻吩分子链方向排列但处于无定形状态的聚噻吩纤维热导率能够达到4.4 W·m−1·K−1[3],可以推测纯净的一维聚噻吩单链晶体当有更为可观的量子热输运能力,12C,32S组成的纯聚噻吩单链中的声子平均自由程大于32 nm.为了便于比较,取L=32 nm,得到T=300 K时32 nm长的纯聚噻吩单链的热导率为30.2 W·m−1·K−1(图6),约为室温下相同长度聚乙烯单链热导率的1/3[16],而与铅的热导率35 W·m−1·K−1相近. 文献[3]运用平衡分子动力学(EMD),在周期性边界条件下,选用ReaxFF势函数计算得到室温下32 nm长聚噻吩单链的热导率为43.3 W·m−1·K−1.另外,文献[17]在MD框架下,同样选取ReaxFF势函数,用格林久保模态分析(GKMA)方法,研究了聚噻吩单链热导率与链长的关系,结果表明室温下32 nm长的聚噻吩单链热导率约7.5 W·m−1·K−1,且在该输运尺度以内,热导率与链长成正比;120 nm长的聚噻吩单链热导率超过120 W·m−1·K−1.该结论有力支持了纯聚噻吩单链中声子平均自由程大于32 nm推测的合理性.从量子力学方法出发可得,室温下32 nm长聚噻吩单链热导率为30.2 W·m−1·K−1,该结果恰好处于EMD和GKMA方法给出的热导率之间(43.3 W·m−1·K−1＞30.2 W·m−1·K−1＞7.5 W·m−1·K−1).我们认为EMD的计算结果偏高是采用经典力学近似和选用的经验势函数ReaxFF导致的.GKMA方法在ReaxFF势模拟基础上考虑了声子之间的相互作用,体现出声子散射的非谐效应,故而得出的热导率7.5 W·m−1·K−1小于我们在弹性输运条件下用量子力学方法计算得到的结果.上述三个独立的理论研究结果一致表明,绝热的聚噻吩材料的热输运潜力十分可观,仍有相当大的提升空间.

T=300 K时12C聚噻吩链中由低到高掺入不同浓度的13C同位素杂质时,体系平均热导变化规律呈U型曲线.这与石墨烯带和硅纳米线热输运的同位素效应规律相似[13,37,38].作为对比,我们计算了纯32S聚噻吩单链中掺入同样比例36S同位素杂质的情形,体系平均热导变化的规律相近,但变化量相对较小.

从图7还可以发现,聚噻吩12C,13C热导的同位素效应在等比例掺杂时最为突出,平均热导比纯净的12C聚噻吩单链降低了31%;32S,36S的情况也是如此,只是其平均热导比未掺杂时降低了9%.12C,13C同位素原子各以50%比例随机掺杂时对声子的散射最强烈,此时平均热导最小.声子与同位素杂质作用时单、多道散射同时存在,且多道散射的影响具有决定性作用,体现出整体的散射行为.误差棒的长度特征表明,同样掺杂比例下,C原子同位素效应引起聚噻吩单链的热导分散性比S原子更加突出.

图6 T=300 K时32 nm长纯12C,32S聚噻吩单链热导率Fig.6.Thermal conductivity of pure12C and32S polythiophene chain with a length of 32 nm at 300 K.

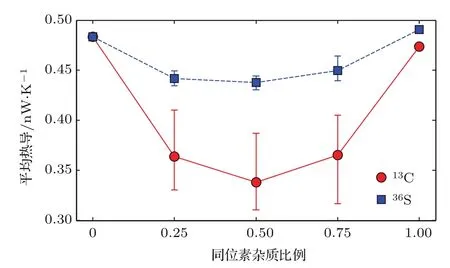
图7 T=300 K时不同13C,36S杂质掺杂比例的聚噻吩单链平均热导Fig.7.Average thermal conductance of polythiophene doped with various13C and36S concentrations at 300 K.

从结构化学的角度来看,C=C键的键能(约600 kJ/mol)比C—S键的键能(约270 kJ/mol)大,即相邻C,C原子间的耦合比C,S原子间的耦合更为紧密,而S的原子质量约为C原子质量的3倍,故S原子的存在将抑制声子沿聚噻吩单链中C—S—C结构的传播,因而聚噻吩单链中的声子主要从相邻C原子为骨架的主链中传输;另外,一个聚噻吩单胞中C原子数与S原子数的比例为4:1,这就意味着同一掺杂浓度下,聚噻吩单链中声子与C原子同位素杂质散射的次数将是S原子同位素杂质数目的4倍.因此,对于同样的随机掺杂浓度,聚噻吩单链中C原子同位素效应导致的体系热导削弱比S原子显著得多.可以推测,同样掺杂比例下,C=C主链上出现C同位素杂质对体系热导的扰动幅度比非C=C主链上出现S原子同位素杂质时更为明显,事实上,图7中,在相同的掺杂比例下,C,S同位素杂质引起体系热导波动的误差棒长度特征有力地印证了这一点.

聚噻吩热导的同位素效应可以作为热导调制的一个有效途径.从散热角度考虑,希望尽量提高聚噻吩的热导率,这对设计诸如聚噻吩单分子发光二极管之类的纳米电子器件,尤其是防止局域热导致的熔断,至关重要;而热电材料的开发却需要抑制聚噻吩热导以提高热电转换效率,这可以通过调节C同位素杂质的最佳掺杂浓度实现.理论预测可知C元素的热导同位素效应比S元素更显著,因而调节效果更佳.

图8所示为T=300 K时,聚噻吩单链中保持32S不变,碳元素分别为12C,13C,14C的质量热导效应曲线;以及保持12C不变,S元素分别为32S,33S,34S,36S的质量热导效应曲线.从图8可以看出,随着C的相对原子质量变大,热导基本呈反比例减小;精确的计算表明,随着S的相对原子质量变大,热导反而缓慢增加,后逐渐趋于恒定.这说明相对原子质量热导效应曲线随着微观体系结构的不同可以有复杂的表现形式,由整个体系的质量分布和力常数张量共同决定.

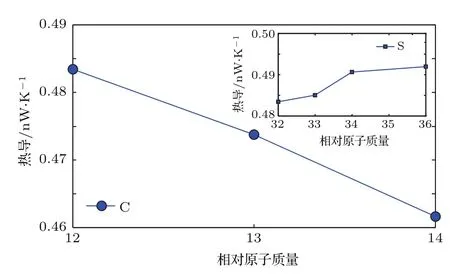
图8 T=300 K时纯聚噻吩单链热导随相对原子质量的变化Fig.8.Thermal conductance of pure polythiophene chain versus relative atom mass at 300 K.

4 结 论

应用DFT,CIS方法结合NEGF方法,预测了室温下32 nm长纯聚噻吩单链热导率的理论上限为30.2 W·m−1·K−1,并与MD方法的结果进行了比较.另外,对长度为25.107 nm、包含448个原子的聚噻吩单链在一般掺杂比例下的热导同位素效应进行了研究,克服了级联散射模型及标度理论仅适用于低掺杂浓度(≤10%)的不足.计算发现,同等掺杂比例下,聚噻吩中C元素热导的同位素效应比S元素更为显著.室温下,12C,13C随机同位素掺杂的聚噻吩单链,掺杂比例为1:1时热导同位素效应最为显著,此时的平均热导比未掺杂前至少降低了30%.这对于认识聚噻吩单链热导的调控因素,挖掘聚噻吩材料在热输运方面的潜力,优化其在有机发光器件、太阳能电池和热电材料方面的性能具有积极的意义.同时,探索准一维高分子链体系热导同位素效应的特点,对于调制纳米线的热导[39,40]及提高纳米材料的热电优值[41,42],也有一定的参考借鉴价值.

[1]Reecht G,Scheurer F,Speisser V,Dappe Y J,Mathevet F,Schull G 2014Phys.Rev.Lett.112 047403

[2]Bulumulla C,Du J,Washington K E,Kularatne R N,Nguyen H Q,Michael C B,Stefan M C 2017J.Mater.Chem.A5 2473

[3]Singh V,Bougher T L,Weathers A,Singh V,Bougher T L,Weathers A,Cai Y,Bi K,Pettes M T,McMenamin S A,Lv W,Resler D P,Gattuso T R,Altman D H,Sandhage K H,Shi L,Henry A,Cola B A 2014Nature Nanotech.9 384

[4]Cowen L M,Atoyo J,Carnie M J,Baran D,Schroeder B C 2017ECS J.Solid State Sci.Technol.6 3080

[5]Chen X B,Duan W H 2015Acta Phys.Sin.64 186302(in Chinese)[陈晓彬，段文晖 2015物理学报 64 186302]

[6]Bouzzine S M,Salgado-Morán G,Hamidi M,Bouachrine M,Pacheco A G,Glossman-Mitnik D 2015J.Chem.2015 296386

[7]Tan Z W,Wang J S,Chee K G 2011Nano Lett.11 214

[8]Xu Y,Chen X B,Gu B L,Duan W H 2009Appl.Phys.Lett.95 233116

[9]Xie Z X,Tang L M,Pan C N,Li K M,Chen K Q,Duan W H 2012Appl.Phys.Lett.100 073105

[10]Ouyang T,Chen Y P,Xie Y,Wei X L,Yang K K,Yang P,Zhong J X 2010Phys.Rev.B82 245403

[11]Zhang H J,Lee G,Fonseca A F,Borders T L,Cho K 2010J.Nanomater.7 537657

[12]Sevinçli H,Sevik C, Çaın T,Cuniberti G 2013Nature.Sci.Rep.3 1228

[13]Chen S S,Wu Q Z,Mishra C,Kang J Y,Zhang H J,Cho K,Cai W W,Balandin A A,RuoffR S 2012Nature Mater.11 203

[14]Chang C W,Fennimore A M,Afanasiev A,Okawa D,Ikuno T,Garcia H,Li D Y,Majumdar A,Zettl A 2006Phys.Rev.Lett.97 085901

[15]Shen S,Henry A,Tong J,Zheng R T,Chen G 2010Nature Nanotech.5 251

[16]Jiang J W,Zhao J H,Zhou K,Rabczuk T 2012J.Appl.Phys.111 124304

[17]Lv W,Winters M,Deangelis F,Weinberg G,Henry A 2017J.Phys.Chem.A121 5586

[18]Gao B,Jiang J,Liu K,Wu Z Y,Lu W,Luo Y 2007J.Comput.Chem.29 434

[19]Jiang J,Liu K,Lu W,Luo Y 2006J.Chem.Phys.124 214711

[20]Taylor J,Guo H,Wang J 2001Phys.Rev.B63 245407

[21]Wang J S,Wang J,Lü J T 2008Eur.Phys.J.B62 381

[22]Yamamoto T,Watanabe S,Watanabe K 2004Phys.Rev.Lett.92 075502

[23]Mingo N,Yang L 2003Phys.Rev.B68 245406

[24]Satoh M,Yamasaki H,Aoki S,Yoshino K 1988Mol.Cryst.Liq.Cryst.Inc.Nonlinear Opt.159 289

[25]Mingo N,Stewart D A,Broido D A,Srivastava D 2008Phys.Rev.B77 033418

[26]Nikolić B K,Saha K K,Markussen T,Thygesen K S 2012J.Comput.Electron.11 78

[27]NIST ComputationalChemistry Comparison and Benchmark Database http://cccbdb.nist.gov/vibscalejust.asp

[28]Hu W P,Jiang J,Nakashima H,Luo Y,Kashimura Y,Chen K Q,Shuai Z,Furukawa K,Lu W,Liu Y Q,Zhu D B,Torimitsu K 2006Phys.Rev.Lett.96 027801

[29]Jiang J,Gao B,Han T T,Fu Y 2009Appl.Phys.Lett.94 092110

[30]Jiang J,Sun L,Gao B,Wu Z Y,Lu W,Yang J L,Luo Y 2010J.Appl.Phys.108 094303

[31]Savic I,Mingo N,Stewart D A 2008Phys.Rev.Lett.101 165502

[32]Stewart D A,Savic I,Mingo N 2009Nano Lett.9 81

[33]Markussen T,Jauho A P,Brandbyge M 2009Phys.Rev.B79 035415

[34]Markussen T,Rurali R,Jauho A P,Brandbyge M 2007Phys.Rev.Lett.99 076803

[35]Rego L G C,Kirczenow G 1998Phys.Rev.Lett.81 232

[36]Fu M X,Shi G Q,Chen F G,Hong X Y 2002Phys.Chem.Chem.Phys.4 2685

[37]Jiang J W,Lan J H,Wang J S,Li B W 2010J.Appl.Phys.107 054314

[38]Yang N,Zhang G,Li B W 2008Nano Lett.8 276

[39]Hu M,Giapis K P,Goicochea J V,Zhang X,Poulikakos D 2011Nano Lett.11 618

[40]Liu Y Y,Zhou W X,Tang L M,Chen K Q 2014Appl.Phys.Lett.105 203111

[41]Zhou W X,Chen K Q 2014Nature.Sci.Rep.4 7150

[42]Zhou W X,Chen K Q 2015Carbon85 24