基于动态混沌映射的三维加密正交频分复用无源光网络∗

林书庆 江宁 王超 胡少华 李桂兰 薛琛鹏 刘雨倩 邱昆

(电子科技大学通信与信息工程学院,光纤传感与通信教育部重点实验室,成都 611731)

1 引 言

随着通信网络的高速发展,信息安全已经成为关系国计民生的重要问题,已经上升至国家战略层面.作为宽带接入网重要支撑技术的无源光网络(passive optical network,PON)技术由于其大吞吐量和高服务质量已经成为最有潜力的宽带光接入解决方案[1−5].在现有PON网络中,基于正交频分复用的无源光网络(orthogonal frequency division multiplexing passive optical network,OFDMPON)由于频谱利用率高、抗色散能力强、资源分配灵活等优势被认为是未来PON接入网的重要发展方向[1,4,5].然而PON网络的开放性使其容易遭受链路窃听、身份冒充等攻击[6,7],因此从物理层提升PON网络数据传输安全性具有重要意义.

混沌系统因其高度的初始敏感性、类噪声、大带宽等特点,在保密通信领域具有重要应用前景.近二十年来,基于激光混沌的物理层加密通信技术已成为保密通信领域的研究热点,研究者们对单/双向耦合激光混沌系统的同步机理、同步条件、同步类型、混沌加密/解密技术、混沌通信性能等各方面进行了详细全面的研究[8−15].2005年,Argyris等[16]在雅典的城市商用光纤网络上成功实现了速率为1 Gbit/s,传输距离为120 km的高速混沌保密通信;该实验证明了高速混沌加密通信的可行性.另一方面,近年来在OFDM调制过程中利用混沌序列对数据进行加密实现高速保密通信成为一个新兴的热点研究课题.目前,国内外学者们已经提出了多种基于混沌的OFDM-PON物理层加密方案[17−24].文献[17,18]利用混沌序列对信息进行频域扰动实现加密,提升通信安全性.文献[19]从时域和频域两个角度对信息进行加密,达到提升安全性的目的.文献[20,21]提出了将分数阶傅里叶变换与混沌加密结合的多维加密方法,并分析了该加密方法对系统峰均功率比(peak to average power ratio,PAPR)的影响.文献[22,23]分析了同时实现信息加密与降低系统PAPR的混沌加密方法,对比了不同加密条件对PAPR下降的影响.文献[24]将混沌序列用于控制相干通信中的正交幅度调制(quadrature amplitude modulation,QAM)以及替换导频和训练序列,从信息、导频和训练序列三个角度进行加密,提升了安全性.上述面向OFDM技术的混沌保密通信技术主要集中于混沌加密方案的研究,而未对混沌密钥分发进行详细探讨.针对此问题,本文提出一种基于动态参数控制的混沌密钥分发方法,并在此基础上提出一种基于动态混沌映射的二重子载波加密和符号扰动的三维加密OFDM-PON.

本文首先介绍了基于动态参数控制的混沌密钥分发方法以及基于动态混沌映射的二重子载波加密和符号扰动的三维加密OFDM-PON系统,然后研究分析了该加密系统的性能及安全性,最后进行基于64QAM调制的13.3 Gb/s@25 km单模光纤传输的OFDM-PON系统实验验证.

2 基于动态参数控制的密钥分发方法

混沌同步是实现密钥安全分发的前提,收发端混沌系统动态同步过程如图1所示.混沌系统的输出序列由系统参数决定,系统参数包含静态参数和动态参数,其中静态参数来自参数集U0,U0中仅包含一组静态参数;动态参数来自于参数集U1,U1中包含多组动态参数,每组动态参数由不同的系统初值和工作参数组成;U0和U1由收发双方按照约定方式产生.

图1 混沌系统的动态同步原理Fig.1.Schematic of the dynamic synchronized chaotic system.

同步过程中,发送方从动态参数集U1中随机选取一组动态参数,并结合静态参数共同控制混沌系统得到长度为l0的二元同步序列L0,然后发送到接收方.

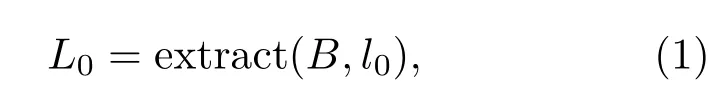
式中B为二元序列,由混沌序列量化产生,运算“extract”表示从B中提取长度为l0的序列L0.

接收方保存接收到的二元同步序列L0,然后从本地动态参数集U1中随机选取一组动态参数用于控制混沌系统产生长度为l0的二元同步序列,并计算L0和的相关系数.由于混沌系统的高度初始敏感性,不同的动态参数组将使混沌迭代的结果不相关,二元同步序列L0和之间相关系数将接近0.接收方在已知动态参数集U1的情况下,经过多次尝试,根据相关系数大小即可判定是否实现了与发送方混沌系统同步.同步后的混沌系统输出序列一致,收发双方利用该同步混沌系统产生混沌序列,并经量化生成密钥,实现数据加/解密.整个密钥分发过程无需进行任何参数传递,有效地提升了密钥的安全性.

3 基于动态混沌映射的三维加密OFDM-PON

以每个ONU连接4个用户为例,对提出的基于动态混沌映射的三维加密OFDM-PON展开分析.加密方案如图2所示.收发双方首先进行混沌同步,然后利用同步混沌系统生成密钥,实现密钥的正确分发,并用于控制信息加/解密.发送端,用户A,B,C,D分别产生一串比特序列,并进行64QAM映射.完成64QAM映射后,发送方提取一定长度的混沌序列经量化生成矩阵M1用于控制子载波映射.

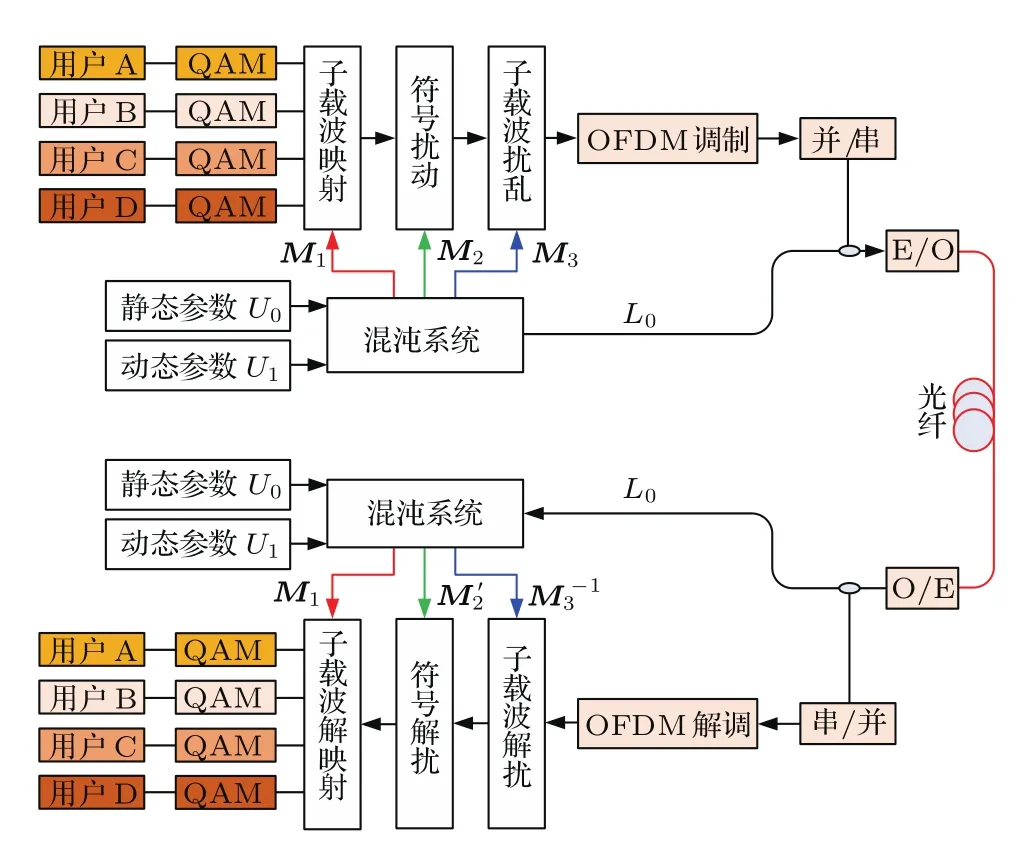
图2 基于动态混沌映射的三维加密OFDM-PONFig.2.Schematic of the three-dimension encryption OFDM-PON based on dynamic chaos-iteration.

设f(f=1,2,···,N)表示子载波,N表示子载波总数,用户A,B,C,D根据M1获取的子载波数分别为NA,NB,NC,ND,且满足

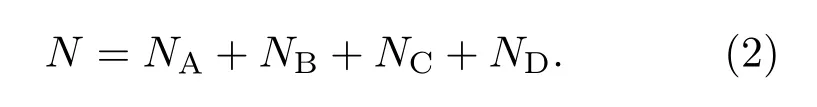
设总的子载波集合为Uf={1,2,···,N},用户A,B,C,D根据M1获取的子载波集合分别为UA,UB,UC,UD,则子载波集合满足如下关系:

将用户A的信息记为SA=A1,A2,···,ANA;用户B的信息记为SB=B1,B2,···,BNB;用户C的信息记为SC=C1,C2,···,CNC;用户D的信息记为SD=D1,D2,···,DND;用户A,B,C,D的信息按照先后顺序依次映射到各自的子载波上.不同的M1控制下,各用户所获取的子载波数目和位置一般不相同,相对应的各用户的信息SA,SB,SC,SD的长度也是动态变化的.定义映射运算符“map”表示子载波映射,则子载波映射过程可表示为

S1为随机子载波映射后的符号矩阵.然后利用一定长度的混沌序列经量化生成符号扰动矩阵M2=[mk,l]实现符号扰动,扰动矩阵M2与符号矩阵S1行列数一致且mk,l=ejB(i),B(i)由混沌序列量化产生.定义矩阵运算“F”表示矩阵对应位置的元素一一相乘,则扰动过程可表示如下:

(10)式中S2为扰动完成后的符号矩阵.最后利用混沌序列量化生成可逆矩阵M3扰乱所有子载波顺序,

(11)式中I为单位矩阵,Ei为初等矩阵;(12)式中S3为扰乱后的符号矩阵.加密完成后的OFDM时域信号可表示为

式中N表示快速傅里叶反变换(inverse fast fourier transform,IFFT)的长度,T为符号周期,f(k)表示第k个子载波频率.

加密完成后,发送方利用IFFT实现OFDM调制,然后进行并串转换,并调制到光载波上.接收方接收到数据后进行串并转换,利用快速傅里叶变换(fast Fourier transform,FFT)完成OFDM解调,然后进行信号恢复、解密和QAM解调.定义运算符“demap”表示子载波解映射,则解密过程可表示如下:

用于产生密钥的混沌系统由二维耦合Logistic映射[23,25]构成,数学模型如下:

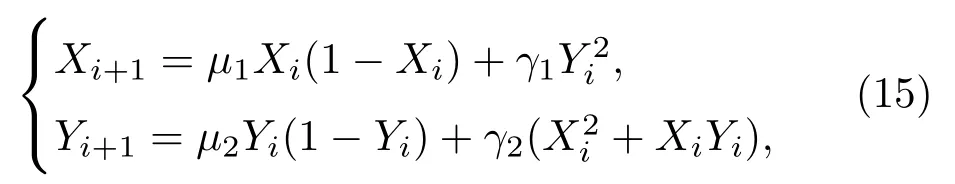
其中参数取值范围满足µ1∈(2.75,3.4),µ2∈(2.75,3.45),γ1∈(0.15,0.21),γ2∈(0.13,0.15),混沌序列Xi,Yi∈(0,1).方案中,规定混沌系统的初值(X0,Y0)为动态参数,由动态参数集合U1确定,任意一组动态参数的取值属于区间(0,1);混沌系统参数µ1,µ2,γ1,γ2为静态参数,由静态参数集合U0确定,分别属于区间(2.75,3.4),(2.75,3.45),(0.15,0.21),(0.13,0.15),静态参数与动态参数的取值均满足二维耦合Logistic系统能进入混沌状态.混沌序列(Xi,Yi)为混沌系统输出序列.为了增强统计特性,将序列(Xi,Yi)进行如下量化操作后,再用于生成密钥,控制加解密处理过程.

(16)式中运算“ fl oor”表示向下取整.

由于加密处理产生的密钥空间大于混沌系统的密钥空间,因此加密方案的安全性主要依赖于混沌系统密钥空间及其输出序列B的安全性.图3(a)—(d)分别给出了混沌系统的初值敏感性、混沌序列Xi、二元序列B、同步序列L0的自相关系数曲线.自相关系数定义如下[26−28]:

其中X表示进行相关性测试的实数序列,i和τ为整数,运算“〈·〉”表示求算数平均值,RXX为X的自相关系数.图3(a)验证了混沌系统的高度初值敏感性(10−15);图3(b)—(d)则分别表明混沌序列Xi、二元序列B、同步序列L0均具有良好的自相关特性.

图3 (a)二维耦合Logistic混沌系统初值敏感性;(b)混沌序列Xi的自相关系数;(c)二元序列B的自相关系数;(d)同步序列L0的自相关系数Fig.3.(a)Sensibility to the initial value X0;(b)self-correlation curves of chaotic sequence Xi;(c)selfcorrelation curves of binary sequence B;(d)self-correlation curves of synchronization sequence L0.

为了验证本方案采用的混沌系统产生的二元序列的随机性,表1给出了随机选择1000组初始值产生的二元序列B的随机性测试结果.这里采用国际标准NIST SP800-22对随机性进行测试,每个样本包含1 Mb的二进制序列,显著水平设为0.01[29].结果表明,序列B能通过标准NIST SP800-22的所有15项随机性测试.结合(15)式,系统输出序列由参数(X0,Y0,µ1,µ2,γ1,γ2)决定, 因此加密方案的密钥空间为5.46×1086(1×1×0.65×0.7×0.06×0.02×1015×6)[23].若用穷举法破解该混沌加密系统,以每秒3.38×1017的运算速度,需要1.61×1069a,这表明该加密方案能够有效对抗穷举攻击.动态参数控制下,任意时刻混沌系统输出均随着初始条件的变化而改变,窃密者在破解混沌系统时,需要同时考虑系统初始敏感性和动态参数的变化,直接跟踪并破解混沌系统更加复杂.同时,动态参数还有助于系统获取更丰富的序列B,增大窃听者破译信息的难度,提升数据传输安全性.

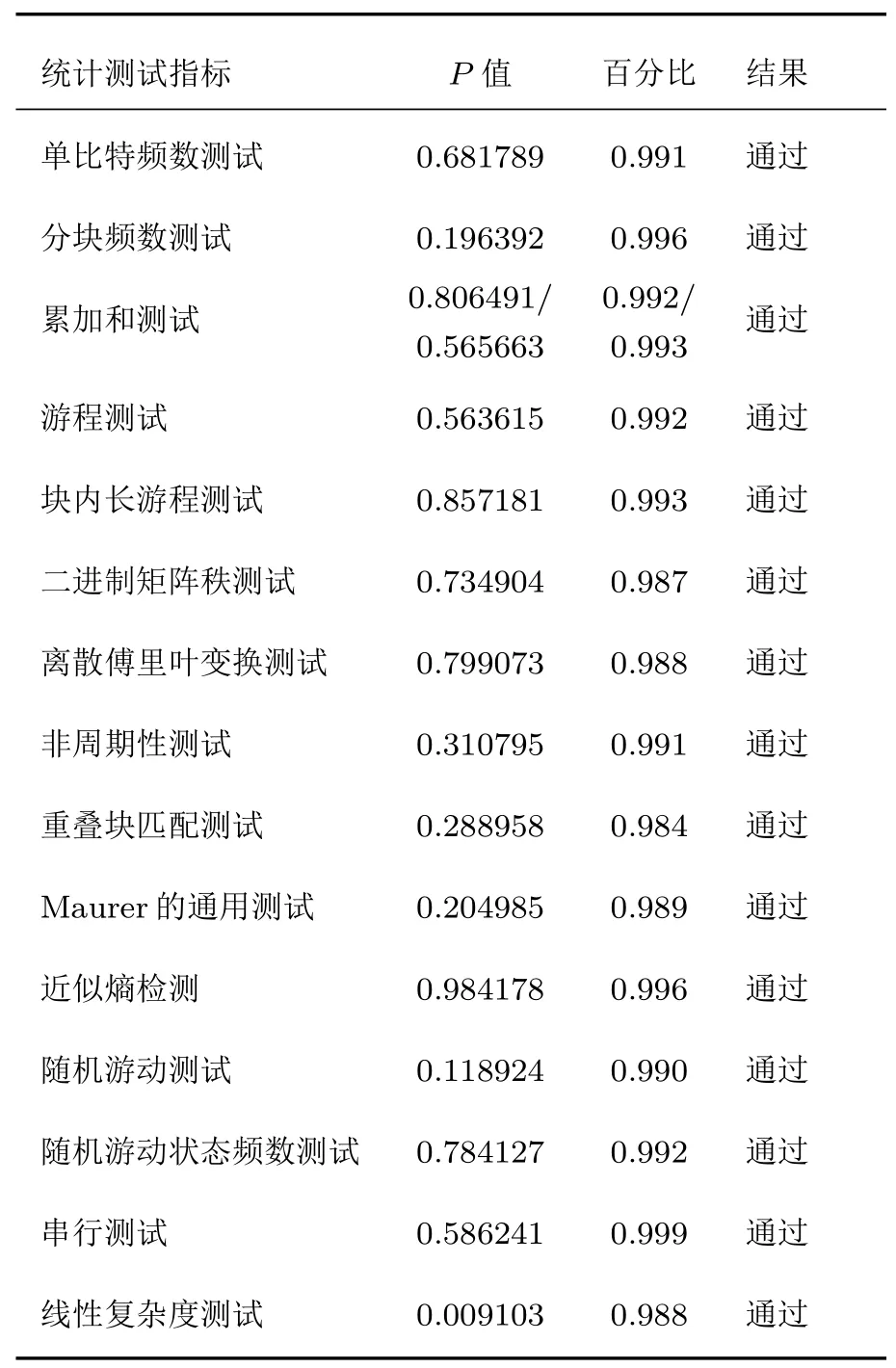
表1 NIST SP800-22随机性测试结果[29]Table 1.Result of NIST SPECIAL PUBLICATION 800-22 TEST[29].

4 实验分析

图4为基于二重载波加密与符号扰动的三维加密OFDM-PON实验系统.该系统包含一个光线路终端(optical line terminal,OLT),两个合法光网络节点(optical network unit,ONU)以及一个窃听ONU.在OLT端,下行数据进行64QAM调制和加密映射到子载波上.为保证OFDM调制信号全为实值,本文利用了Hermitian对称结构[22],即在512个子载波中,仅255个子载波传输64QAM数据,1个子载波作为直流分量,IFFT的长度为512.OFDM调制完成后,进行并串转换,然后插入1/8符号长度的循环前缀.以上过程均通过线下处理实现.加密OFDM信号被加载到符号率为5 Gs/s的任意波形发生器(AWG7102)产生OFDM电信号,并通过MZ调制器调制到波长为1550 nm光载波上.加密OFDM信号时域波形以及频谱如图5所示,信号带宽为2.5 GHz,信息速率为13.3 Gb/s(5 Gs/s×log264×8/9×255/512).在ONU端,接收信号经过带宽为10 GHz的光电探测器(photodiode,PD)后,利用数字示波器(采样率25 Gs/s)保存,然后通过线下处理依次进行OFDM解调、信号恢复、解密和QAM解调.

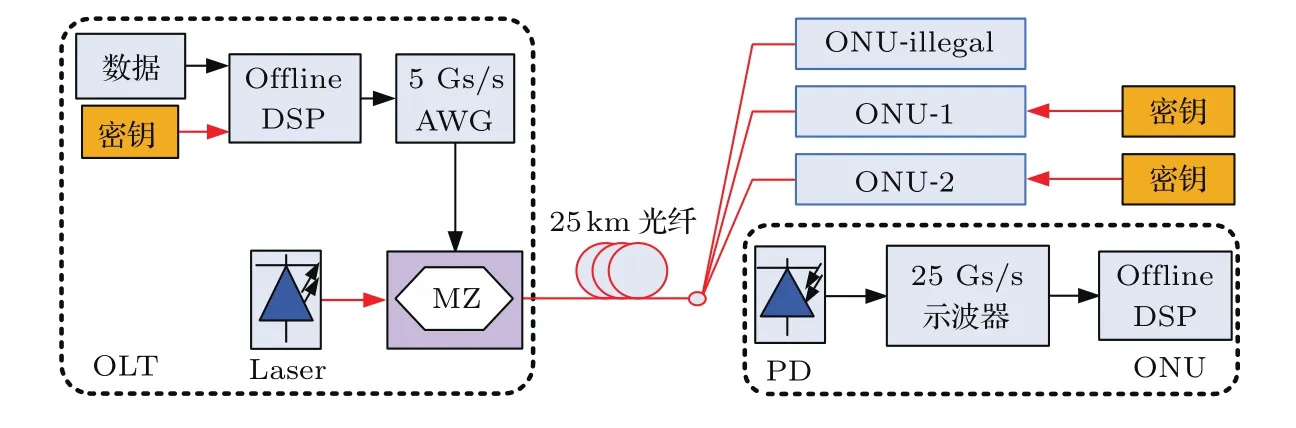
图4 三维加密OFDM-PON的实验系统设置Fig.4.Experimental setup of the proposed three-dimension encryption OFDM-PON.

进行数据解密前,接收方首先需要实现与发送方的混沌同步.通过计算机仿真模拟该过程,得到如图6所示的仿真结果. 静态参数µ1,µ2,γ1,γ2的取值分别为3.20,3.05,0.17,0.14,动态参数集U1包含100组动态参数,且任意一组动态参数(X0,Y0)i的取值属于区间(0,1),静态参数与动态参数均满足系统能进入混沌状态,同步序列L0的长度为1000.根据图6中的结果,当且仅当i=50收发双方动态参数一致,同步序列L0与L′0相关系数为1,即接收方实现了与发送方的混沌同步,而其余动态参数控制下,相关系数均小于0.1,接收方未实现与发送方混沌同步.

图5 (a)加密OFDM信号时域波形;(b)加密OFDM信号频谱Fig.5.(a)Temporal waveforms and(b)spectrum of the encrypted OFDM signal.

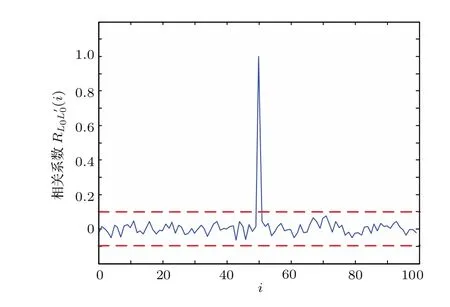
图6 同步序列L0与的相关系数Fig.6. Correlation curves of synchronization se-quencesL0and.

图7给出了合法用户和非法窃听者解密信息的误比特率随接收光功率的变化曲线,以及接收光功率为−7 dBm时加密信号经25 km标准单模光纤传输后的合法用户与窃听者的星座图.实验结果表明:对于背靠背传输和经25 km标准单模光纤传输的加密OFDM信号,当接收光功率分别大于−11和−8 dBm时,合法用户的误比特率下降到FEC(forward error correction,FEC)限以下,即合法用户能够正确获取有效信息;对于窃听者,由于无法获取密钥进行解密,其星座图处于混乱状态,误码率始终在0.46附近,无法获取有效信息.值得注意的是,相较于普通OFDM信号传输,本文提出的三维加密OFDM信号的传输不会造成系统额外的光功率代价.加密前后各子载波上的QAM符号归一化幅值统计如图8所示.统计结果表明,加密处理使得QAM符号的归一化幅值分布更加丰富,有效地掩盖了原始的QAM符号统计分布特性,有利于抵抗统计分析攻击,提升安全性.

图7 合法接收和非法接收误比特率随接收光功率的变化Fig.7.BER curves for legal decryption and illegal decryption versus the received optical power.

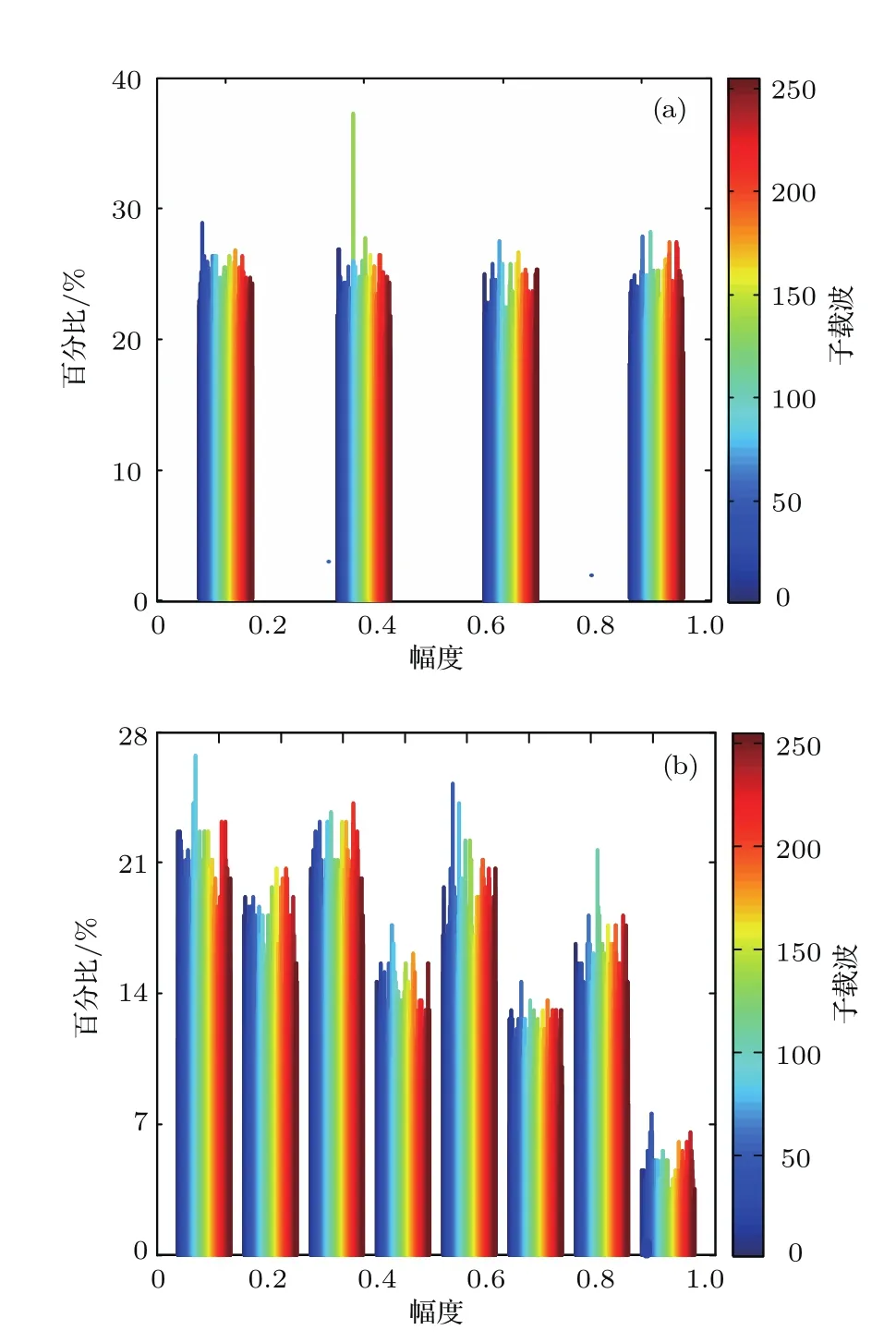
图8 子载波QAM符号归一化幅值统计百分比 (a)加密处理前;(b)加密处理后Fig.8.Statistical histograms with subcarriers of 255:(a)Before QAM symbol scrambling;(b)after QAM symbol scrambling.

5 结 论

利用混沌系统的初始敏感性和相关性检测方法,提出了一种基于动态同步的密钥分发方法.该方法可以增加密钥系统的复杂度,增大破解混沌系统的难度,并有助于获取更丰富的密钥序列,增加破译信息的难度;此外,该方法也无需传递任何系统参数,可以有效提升密钥安全性;通过分析密钥生成系统的初始值敏感性和混沌序列的相关性以及基于混沌的二元序列的随机性表明,该密钥分配系统密钥空间可达1086以上,能有效抵抗穷举攻击.在此基础上,通过对OFDM信号进行二重混沌子载波加密和符号扰动,建立了一种三维加密OFDM-PON系统.实验结果表明,合法解密可以正确恢复信息,而非法窃密者的误码率始终在0.46附近.本文提出的基于动态混沌映射的三维加密OFDM-PON能够有效提高信息传输安全性.

[1]Zhang J,Qiu K,Bao W B,Deng M L,Li Y G,Zhang H B 2009China Commun.2009 103

[2]Cvijetic N,Qian D Y,Hu J Q 2010IEEE Commun.Mag.48 70

[3]Qian D Y,Cvijetic N,Hu J Q,Wang T 2010J.Lightwave Technol.28 484

[4]Qiu K,Yi X W,Zhang J,Zhang H B,Deng M L,Zhang C F 2011Proc.SPIE8309 1

[5]Zhang L J,Xin X J,Liu B,Yu J J,Zhang Q 2010Opt.Express18 18347

[6]Ren J Y 2009Netinf.Security2009 61(in Chinese)[任建勇2009信息网络安全2009 61]

[7]Peng D Q,Gu Y,Wan L Y,Chen Y 2015Video Engineer.39 50(in Chinese)[彭大芹,谷勇,万里燕,陈勇2015电视技术39 50]

[8]Wu L C 2006China Water Transport6 125(in Chinese)[吴立春2006中国水运(学术版)6 125]

[9]Liu L Z,Zhang J Q,Xu G X,Liang L S,Wang M S 2014Acta Phys.Sin.63 010501(in Chinese)[刘乐柱,张季谦,许贵霞,梁立嗣,汪茂盛2014物理学报63 010501]

[10]Li X F,Pan W,Ma D,Luo B,Zhang W L,Xiong Y 2006Acta Phys.Sin.55 5094(in Chinese)[李孝峰, 潘炜,马冬,罗斌,张伟利,熊悦2006物理学报55 5094]

[11]Cao L P,Xia G Q,Deng T,Lin X D,Wu Z M 2010Acta Phys.Sin.59 5541(in Chinese)[操良平,夏光琼,邓涛,林晓东,吴正茂2010物理学报59 5541]

[12]Zhao Q C,Wang Y C 2010Laser Optoelectron.Prog.47 030602(in Chinese)[赵清春,王云才2010激光与光电子学进展47 030602]

[13]Zhao Y M,Xia G Q,Wu J G,Wu Z M 2013Acta Phys.Sin.62 214206(in Chinese)[赵艳梅,夏光琼,吴加贵,吴正茂2013物理学报62 214206]

[14]Xiang S Y,Wen A J,Pan W,Lin L,Zhang H X,Zhang H,Guo X X,Li J F 2016J.Lightwave Technol.34 4221

[15]Xue C P,Jiang N,Lü Y X,Wang C,Li G L,Lin S Q,Qiu K 2016Opt.Lett.41 3690

[16]Argyris A,Syvridis D,Larger L,Annovazze-Lodi V,Colet P,Fischer I,Garcia-Ojalvo J,Mirasso R C,Pesquera L,Shore K A 2005Nature438 343

[17]Zhang L J,Xin X J,Liu B,Yu J J 2012Opt.Express20 2255

[18]Liu B,Zhang L J,Xin X J,Liu N 2016IEEE Photon.Technol.Lett.28 2359

[19]Zhang L J,Liu B,Xin X J,Zhang Q,Yu J J,Wang Y J 2013J.Lightwave Technol.31 74

[20]Deng L,Cheng M F,Wang X L,Li H,Tang M,Fu S N,Shum P,Liu D M 2014J.Lightwave Technol.32 2629

[21]Cheng M,Deng L,Wang X,Li H,Tang M,Ke C,Shum P,Liu D 2014IEEE Photon.J.6 1

[22]Hu X L,Yang X L,Shen Z W,He H,Hu W S,Bai C L 2015IEEE Photon.Technol.Lett.27 2429

[23]Zhang W,Zhang C F,Chen C,Jin W,Qiu K 2016IEEE Photon.Technol.Lett.28 998

[24]Jin W,Zhang C F,Yuan W C 2016Opt.Engineer.55 026103

[25]Wang X Y,Shi Q J 2005Chin.J.Appl.Mech.22 501

[26]Zhang J Z,Wang A B,Wang J F,Wang Y C 2009Opt.Express17 6357

[27]Jiang N,Pan W,Yan L S,Luo B,Zhang W L,Xiang S Y,Yang L,Zheng D 2010J.Lightwave Technol.28 1978

[28]Wu J G,Wu Z M,Liu Y R,Fan L,Tang X,Xia G Q 2013J.Lightwave Technol.31 461

[29]Zhang L M,Pan B W,Chen G C,Guo L,Lu D,Zhao L J,Wang W 2017Sci.Rep.8 45900