风轮模型设计与试验

程 振，张新荣，刘成浩，陈俊杰

（中水东北勘测设计研究有限责任公司，吉林 长春 130021）

1 概述

风能作为一种分布广泛的、无污染的可再生能源，风能越来越受到人们的重视。空气的流动就是风，风能所指的是风的动能。一定风速的风吹在静止的的风力机叶片上做功并驱动发电机发电，将风能转化为电能。文章介绍的是一种木质结构的风轮模型，它在实验室模拟的风速下转动并驱动直流发电机工作。

为深入探索风力发电原理，笔者实验自制小型“定向木结构风力发电塔”，模型包括0.8 m高的塔身和直径0.8 m的叶轮，叶轮在7档风速下旋转（特征风速6.8 m/s）。由于模型尺寸很小，制作材料为木材，在初步设计计算时各参数具体取值缺乏理论指导，所以只能通过模型的功率测试试验，到最大功率时各个参数的取值，从而改进模型设计方案、提高模型的性能。

2 风轮模型设计方案

2.1 风轮理论有效功率P

风轮有效输出功率计算：

式中：P——风力机输出功率，W；ρ——空气密度，kg/m3，取1.225；V——设计风速，取特征风速6.8 m/s为设计风速；R——风轮半径，取0.4 m；η1——发电机效率；η2——传动效率；Cp——风能利用系数。

由贝茨理论可知，理想风能对风轮叶片所做功的最高效率是59.3%，通常风力机风轮叶片接收风能的效率达不到最高，设计时风能利用系数范围为0.25～0.45。由于风轮模型与发电机直接用转盘相连接，η2可视为1。将η1η2视为整机效率，取值近于发电机效率，取为0.85。

风轮模型有效输出功率计算结果，见表1。

表1 模型理论有效功率

2.2 风轮模型叶片外形设计

翼型对风力机叶片很重要，直接影响风轮的启动及接收风能的效率。一种较好的翼型应该是在某一攻角范围内升力系数CL较高，而相应的阻力系数CD较小。风轮模型翼型为FX63-137，该翼型最大升阻比105为设计值，叶片设计迎角4°。

Wilson模型气动计算方法是目前国内外应用最普遍的叶片设计方法之一，该方法计算精度高，考虑了升阻比对叶片最佳性能的影响及风轮在非设计状态下的性能。以MATLAB的计算功能为基础，采用Wilson方法考虑升阻比对叶片最佳性能的影响及风轮在非设计状态下的性能进行编程，从而将计算机语言与叶片设计结合起来，解决非线性有约束最大化问题，为优化设计提供便利条件。

简化数学模型目标函数：

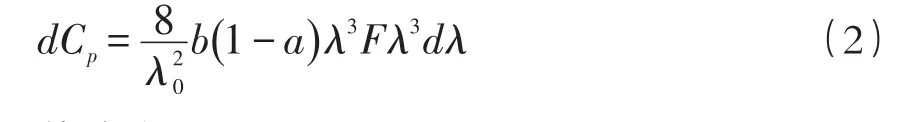
约束条件：

干涉因子a，b可以有经验公式求得：

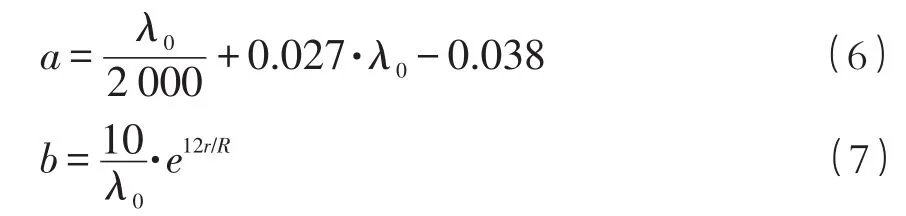
式中：λ0——叶尖速比，取1；R——风轮半径，取0.4 m；r——叶片从转动中心至叶尖的不同位置的半径，m；B——叶片数；C——每个叶片剖面的弦长，m。

风轮模型叶片外形设计计算结果见表2。

设计模型为木质结构，不易扭曲，因此制作时将叶片做成等安装角叶片。叶尖处单位长度叶片的扫掠面积大，起重要作用，在其附近可取得取最佳安装角。在叶片制作过程中整个叶片的安装角尽量靠近18.9°，暂取为19°。

风轮模型叶片初步设计结果见表3。

风轮模型叶片效果图见图1。

3 风轮模型发电功率测试实验方法

3.1 风的模拟与风速测量

在开阔的实验场内，风由轴流鼓风机模拟，采用手持式三杯风向风速表测风速。风速仪沿风轮模型中心与鼓风机中心连接线测量。鼓风机开机3 min后开始测量，为了防止测量时手持风速仪的抖动所造成的偏差，确保测量数据的准确性，每一档风速测试3组数据后取平均值，平均风速见表4。

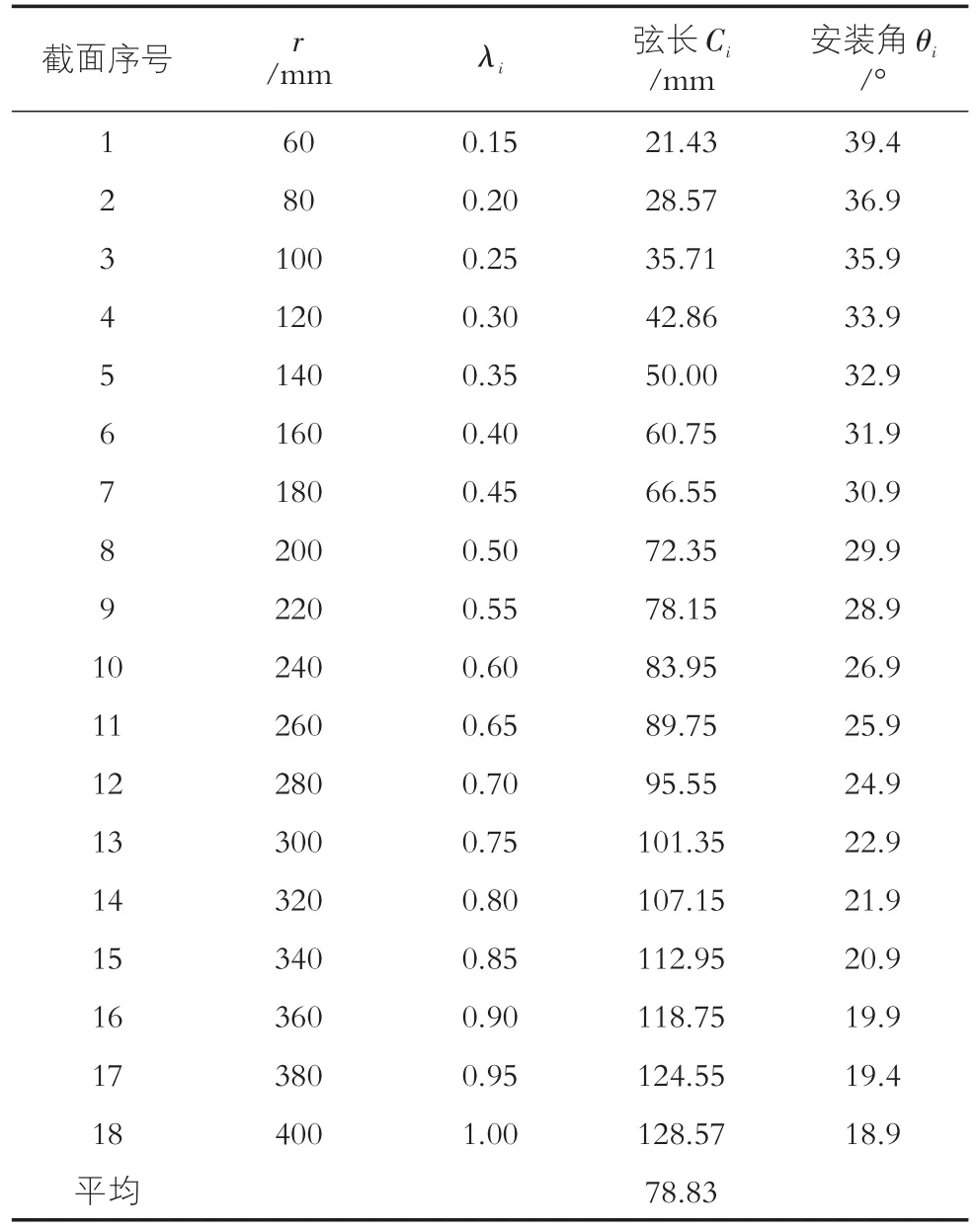
表2 风轮模型叶片外形设计计算结果表

表3 风轮模型叶片初步设计成果表

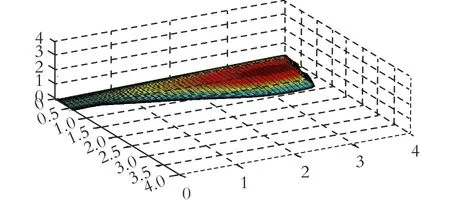
图1 叶片MATLAB效果图

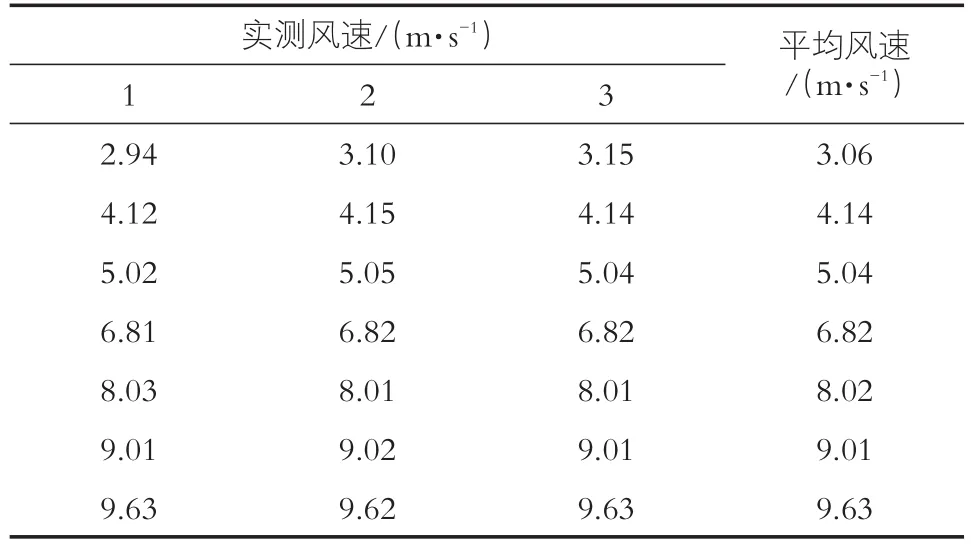
表4 模拟风速测试成果表

3.2 功率测试

用数字万用表测负载两端电压，测量模型发电功率时，外接负载为1.5 Ω。

负载电压和电功率之间的关系为：

式中：P——输出功率，W；U——负载实测电压，V；R——负载电阻，Ω。

6叶片19°安装角的风轮模型的功率测试成果见表5。

表5 6叶片19°安装角风轮模型功率测试成果表

4 试验内容及结果

风轮模型功率测试结果与理论模型有效功率对比可见，模型设计尚有改进空间，优化设计模型叶片数及安装角，从而得到发电功率大、模型重量轻的风力发电塔模型。

4.1 模型叶片数改进方案

固定叶展形状及安装角，测试叶片数分别为3，4，6片的3种风轮模型发电功率，测试结果，见表6。

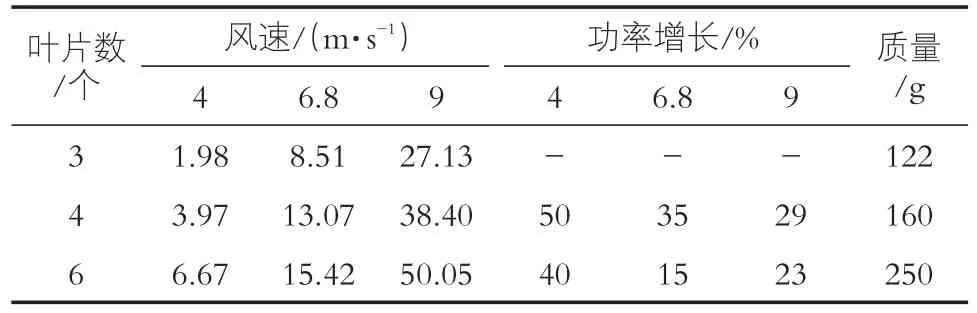
表6 不同叶片数功率测试成果表

由表6可知，在同档风速下，模型发电功率是随着叶片数目增多而有着不同程度的增长。3个叶片模型的发电功率最低，4个叶片模型较3个叶片模型的功率增长率最大，远大于6个叶片模型较4个叶片模型的功率增长率。显然6个叶片模型发电功率大，但提高幅度不大，质量增加却过多。优化设计方案确定叶片数目为4个更为合适。

4.2 模型安装角改进方案

叶片安装角指风轮旋转平面与翼弦所成的角。模型叶片为木质结构不易扭曲，是等安装角叶片。测试安装角分别为27°，25°，20°，18°的4种模型，不同模型安装角功率测试结果见表7。

表7 四叶片不同安装角度功率测试结果表

由表7可知，安装角度20°时模型发电最大，优化设计方案确定风轮模型安装角度为20°更为合适风轮模型优化设计方案的功率与风速关系测试结果见表8。

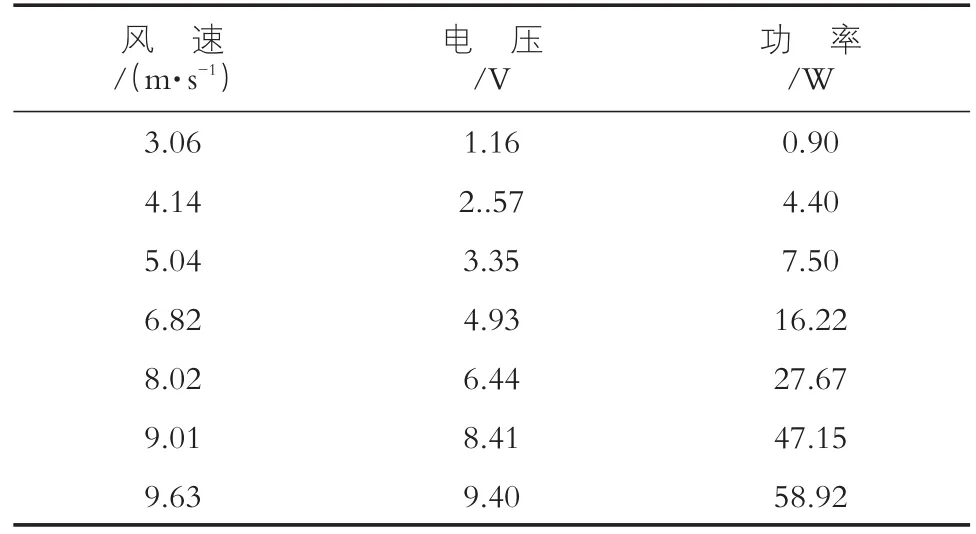
表84 叶片20°安装角风轮模型功率测试成果表

风轮模型理论有效功率及优化方案发电功率对比见图2。

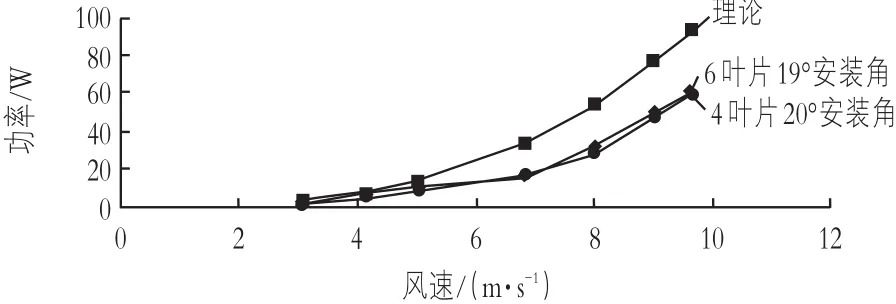
图2 风轮模型理论有效功率及优化方案发电功率对比图

5 总结

依据理论知识，设计了一种小型木质风轮模型，对不同叶片数及安装角度的模型进行功率测试试验。

1）从图2中可以看出模型改进前后的实测发电功率均小于理论计算值。理论计算为扭曲叶片，即叶片各处安装角各不相同，角度至叶尖处达到最小，从而使叶片各处都在最佳迎角状态，以获得最佳升力。而模型制作时，叶片材质不易扭曲而做成等安装角叶片，等安装角叶片无法满足各处都处于最佳迎角状态，使得风能利用效率降低，故低于理论计算值。

2）叶片等安装角度的设计方案对功率输出有很大影响。模型输出功率会随着安装角度的增大而增大，但是超过20°角范围后范围而下降，这样通过实验测试功率的方法找到本模型的安装角限值。

3）虽然优化设计后模型发电功率与优化设计前的差距不大，但是模型质量却从250 g降低至160 g，提高了模型质量优势，因此优化设计方案是合理可行的。

［1］郭新生.风能利用技术［M］.北京：化学工业出版社，2007.

［2］丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京：机械工业出版社，2005.

［3］薛扬，秦世耀.重视开发风电机组检测技术［J］.中国科技投资，2008（4）.

［4］邝朴生，徐福章，刘玉琴.现代机器故障诊断学［M］.北京：农业业出版社,1991.

［5］R.A.柯拉科特.机械故障的诊断与情况监测［M］.北京：机械工业出版社，1983.

［6］樊永生.机械设备诊断的现代信号处理方法［M］.北京：国防工业出版社,2009.

［7］张新荣.风力发电机组主要结构振动特性及检测技术研究［D］.武汉：武汉大学，2011.