弱胶结地层立井井筒变形监测研究

，，，，

(1. 山东科技大学 a.土木工程与建筑学院；b.矿山灾害预防控制省部共建国家重点实验室培育基地；c. 矿业与安全工程学院，山东 青岛 266590；2.山东新巨龙能源有限责任公司，山东 菏泽 274918)

1 研究背景

弱胶结地层表土段通常为深厚松散沉积层，主要由第三纪、第四纪以来沉积成层、尚未固结硬化成岩的疏散沉积物构成，其基岩段主要为砂层，富含水且岩层强度较低[1-3]。这类地层受含水层渗流压缩影响，易导致上覆土层失水压缩变形[4-5]。因此，混凝土和岩土体蠕变、损伤、地层渗流压缩及冻融效应等多因素耦合作用导致立井井壁产生疲劳累积，引起井壁的局部变形过大，造成混凝土井壁破损进而形成环状破裂带，诱发立井井筒的灾变。例如，1995年兖州兴隆庄西风井在使用20 a后，井壁石料沿剥裂面剪断，剥离高度达100～200 mm，横筋露出，裂缝处涌水量达20 m3/h，造成经济损伤达数百万之多[6]。据不完全统计[7-8]，自20世纪80年代以来，我国目前有百余个井筒已发生井壁破裂或存在破坏危险。井壁长期处于工作状态，其变形破坏具有隐蔽性和突发性，在短时间内就可能演化成井壁溃塌灾害，造成极大的生命财产损失。

立井井筒的安全评估与破坏预测对于有效地避免矿山特殊工程地质灾害有着重要意义。常用方法是利用数学模型和数值模拟进行井壁破裂极限预测。如刘环宇等[9-10]建立了井筒非采动破裂的非线性预测与判别方法；邵良杉等[11]建立了基于组合技术的立井井筒变形破坏KNN预测模型，并使用测试数据对模型进行测试；袁志刚等[12]考虑井筒变形破坏的多个影响因子，建立了煤矿立井井筒非采动破裂的遗传-支持向量机预测模型，为快速准确地预测立井井筒非采动破裂提供了一种新的方法和途径；张向东等[13]以弹性理论为基础，运用MatLab软件建立了井壁破坏预测的数学模型，进而对井壁的受力变形情况进行了预测分析；许延春等[14]利用改进的经验拟合法和多元统计距离判别法，以兴隆庄煤矿主井、副井、东风井和西风井为例，对其井筒安全性进行了评价；陈祥福等[15]、王传武[16]、张辉[17]采用数值模拟方法对井壁破坏时的应力应变情况以及塑性区的范围、破裂形态、破裂时间等问题进行了研究。弱胶结地层立井井筒的变形破坏是多因素综合作用下的渐进式动态过程，因此在井筒破坏预测方面，理论计算和数值模拟方法均存在一定的局限性。理论计算过程中应用大量的假设，将复杂问题理想化；而数值模拟方法往往忽略动力扰动、时空效应等诸多可变因素，从而导致计算结果与实际结果存在一定偏差。

微变形监测作为一种动态实时的测试技术，在立井井筒变形监测中发挥着极其重要的作用。如Chai等[18]、邱标[19]、刘化宽[20]、黄明利等[21]提出了以光纤光栅技术为主的变形监测方法，建立了光纤光栅与井壁的应变传递关系，能够预测井筒真实受力变形情况，为井筒的破坏预测提供了依据。王渭明等[22]利用正交试验确定井筒测试位置，实现了立井全深度、多层位、智能化监控的目标。但目前我国的立井井筒信息化程度远低于水利、桥梁等工程领域，监测系统实现智能化、信息化存在以下几个方面的问题：①井筒测试环境复杂恶劣，井壁结构特殊，测试精度要求高；②井壁的破坏位置存在一定的不确定性，多区域连续监测又需兼顾成本；③监测系统的智能化程度不高，难以实现动态反馈。

已有的研究成果表明[23-24]，立井井筒在发生变形破坏之前，会产生明显的变形。为此，在综合分析地层特征及已有工程实践的基础上，建立智能监测系统实现弱胶结地层立井井壁的实时动态监控，结合理论模型预测井壁变形极限值，掌握井筒的变形规律，预测井壁的破坏时间和部位，对于弱胶结地层及类似地层中立井井筒灾变控制有着十分重要的意义。

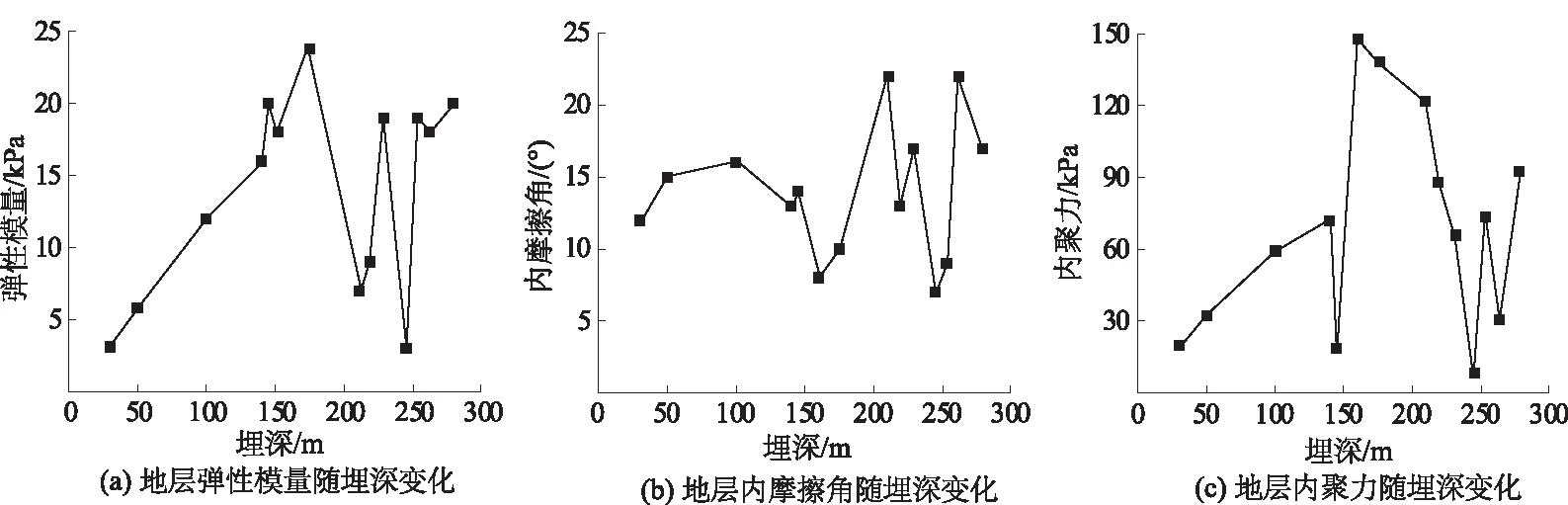
图1 岩土体各参数随地层深度变化曲线Fig.1 Parameters of rock-soil varied with buried depth

2 工程地质概况

新巨龙煤矿位于山东省菏泽市巨野县龙固镇，副井建成于2003年，井筒深度为780 m，弱胶结松散层(表土)厚度为320.5 m，底部含水层厚度为50 m，井筒净直径为8.0 m。表土段采用双层钢筋混凝土井壁，其厚度为1.1～1.8 m，基岩段为普通素混凝土井壁，其井壁厚度800 mm。

新巨龙煤矿井田基岩被厚度介于390.35～509.10 m之间的西北厚东南薄的新生界松散层覆盖。弱胶结地层的松散层主要矿物组成为“次生矿物”(岩石风化的产物)，厚度为50～500 m。该地层沿深度方向松散层由若干含水层和隔水层相间构成，如表1所示。弱胶结松散沉积层是高度分散、富含空隙的三相体系，松散层处于塑性状态的黏土中，其颗粒之间不是直接接触，而是通过水化膜接触，因此，松散沉积物质之间的连接强度很弱，地层呈现弱胶结特性。

表1新巨龙矿区弱胶结地层结构组成
Table1StructuralcompositionofweaklycementedstratainXinjulongminingarea

岩层厚度/m参数岩性第1含水层26q=0．021～0．603L/(s·m)中细粉第1隔水层25IP=17～22砂质黏土第2含水层65q=0．199～2．73L/(s·m)中细砂第2隔水层70IP=18～29黏土第3含水层175k=3．22～12．14中粗砂第3隔水层40IP=20～30黏土第4含水层50q=0．524～1．935L/(s·m)中粗砂第4隔水层20—固结黏土

注：q为单位涌水量；k为渗透系数；Ip为塑性指数

根据Mohr-coulomb准则[25-27]，反映岩土体强度的主要指标有：弹性模量E，内聚力c和内摩擦角φ。如图1所示，在弱胶结地层中随着地层深度的增加，饱和黏土的强度指标变化并不是线性的[28]。地层各强度参数随着深度的增加而上下波动，即弱胶结地层具有明显的分层性，且分层强度差别较大，因此各个分层之间会产生强弱差异面。而在井壁深度方向强弱差异最大的位置最易发生变形破坏。

3 弱胶结地层立井井壁变形极限分析

3.1 井壁变形破坏的极限受力状态响应模型

根据井筒的非采动变形破坏特征可知，井壁在地层中处于三向受压状态，井壁的破坏是竖向、径向以及环向三向应力共同作用的结果[29-30]。井筒内壁径向压力为0，井壁为处于两向受压状态的危险截面。因此，井筒的变形破坏一般从井筒内壁开始，逐渐向井筒外壁扩展，最终贯通。当井筒内壁破裂后，暴露的井壁依然处于两向受力状态，因此，可以采用双向受压混凝土强度破坏准则，即第四强度理论(能量理论)来判断井壁的极限状态，即

(1)

式中：σ2为第2主应力(MPa)；σ3为第3主应力(MPa)；σa为混凝土的设计强度应力(MPa)。

立井井筒可以假设为两端均匀分布、纵向线性分布压力的空间轴对称厚壁圆筒[31-33]。对于厚壁圆筒问题，顶部所受均匀分布荷载P的大小为

(2)

式中：ur=ra为井壁径向位移;K为侧压力沿纵向的分布斜率，一般取13 kN/m，K=q/H，q为井壁侧向压力,H为底部含水层埋深(m)；h为底部含水层的厚度(m)；μ为厚壁圆筒的泊松比；E为厚壁圆筒的弹性模量；ra和rb分别为井筒内、外壁半径(m)。

井筒所受纵向荷载主要由2部分组成，井筒自重G、上覆厚表土层的附加应力叠加值σA，即有P=σA+G，G=γcH，γc为混凝土重度，一般取值为25 kN/m3。由此可得附加应力叠加值σA为

(3)

弱胶结地层底部含水层与基岩段交界处的立井井壁最易发生变形破坏，即表土层与基岩的交界处井壁最易破坏。根据文献[34]，该区域所受应力状态为

(4)

式中:σ1,σ2,σ3分别为井筒内壁第1、第2、第3主应力；σr为径向应力；σθ为切向应力;σz为轴向应力；τrθ为切向应变。

按照极限状态求解，即井筒内壁钢筋混凝土达到极限抗压强度，此时竖向应力σz即为井筒内壁竖向极限承载能力，由此可得

(5)

取最大值可得

(6)

将式(4)代入式(6)可得极限状态下井壁附加应力为

(7)

3.2 极限破坏状态下井筒内壁变形值

新巨龙煤矿井筒主要参数如表2所示。

表2 立井井筒特征参数Table 2 Parameters of shaft lining

将表2的参数代入式(2)、式(3)可得

σA=6.003×104ur=ra-85.9 。

由式(7)可得

由此可得极限破坏状态下井筒内壁变形值ur=ra=2.369 mm。

4 弱胶结地层立井井筒变形监测系统

4.1 测试系统总体构成

立井井筒变形监测系统主要由数据采集模块(多通道无线静态应变测试仪)和传感器系统组成，采集模块采集的数据通过导线传输进静态应变仪，应变仪对数据综合和分析后，可以通过有线和无线2种组网方式，将数据传输进计算机，计算机进行数据分析和采集，通过观察分析数据的变化，对参数进行实时的监控，判断系统变形参数是否在正常工作变形范围内。测试系统整体布置如图2所示。测试系统配置主要包括：主机、JM1900USB总线转换器、稳压电源、位移传感器、超五类网线、系统软件。

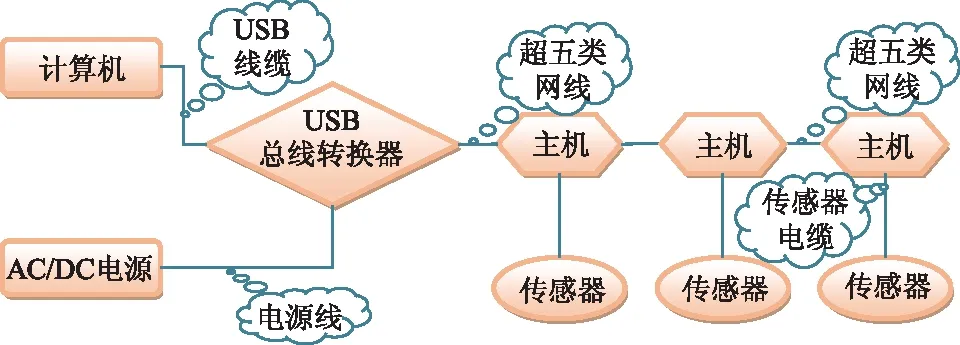
图2 测试系统整体布置Fig.2 Diagram of the test system

测试系统位移传感器选用电阻式线性位移传感器。它具有线性度、分辨率都比较高，失真小的优点，其线性精度为0.3%，温漂系数为1.5×10-6/℃。考虑到井筒潮湿、漏水，位移传感器采用了防水设计。防水设计主要包括航空插头式通讯电缆接头与硅胶防水套，如图3所示。

图3 位移传感器Fig.3 Displacement sensor

4.2 测试系统布置

根据近年来众多学者专家对井筒破坏原因的分析，以及对井筒破坏位置的汇总比较，结合测试矿区典型地质特征，本着精简测点、节约成本、突出重点、力求创新的原则，在有可能发生变形破坏的井筒设置3个监测区域站(以下简称测区)。3个测区的位置分别为：第1测区，新生界含水层与隔水层交界处；第2测区，底部含水层与基岩交界处；第3测区，井筒马头门顶部。

综合考虑水文、地质条件，国内外研究现状以及目前各个井筒的生产状况等因素，满足降低测试费用、减少对生产井筒正常使用干扰的要求，将理论研究与现场测试有机结合，力求用最少的测试参数反映出最全面的有效信息。考虑岩层倾角不大，地压沿井筒切向分布存在对称性，3个测区选用相同的测试方式，每层测区对称选择4个测点，每个测点测试内容包括井壁纵向位移和井壁径向位移。

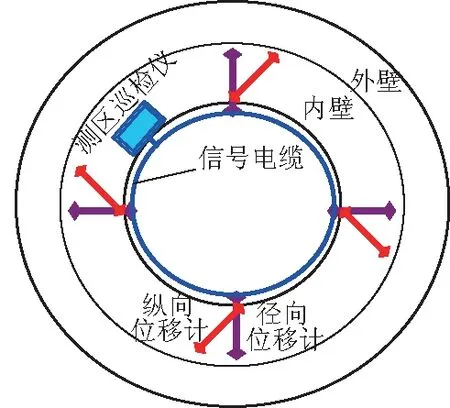
图4 测试断面元件布置Fig.4 Arrangement of elements in the test section

测区元件布置如图4所示。每个测区布设一台智能控制的分站检测仪，负责本测区各测点的定期检测和定时采样，并将测试数据传输到总站检测站；总站检测仪安装在地面，负责向各分站检测仪发送检测指令，接收分站传来的检测信息，并将检测信息及时送到计算机，通过信息反馈分析，出现井壁破裂险情时，发出报警指令。

4.3 监测预警设置

监测系统可根据前述理论模型得到的井壁变形极限值设定立井井壁变形预警的阈值。相应的传感器超出设置的报警界值后进行颜色或声音报警。根据立井井壁变形程度不同，可设置二级预警系统。如图5所示。

一旦井壁变形超出上、下常态值时进行预警，超出上、下预警界值时进行报警。

测试系统将每个监测断面的监测分站用信号电缆串联起来，沿灌道梁引到地面上，测试系统信号传输如图6所示。

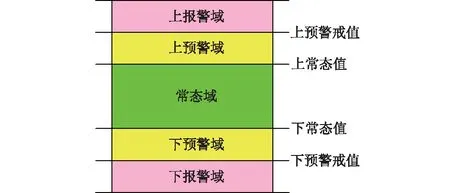
图5 监测预警分级Fig.5 Grading of monitoring warning

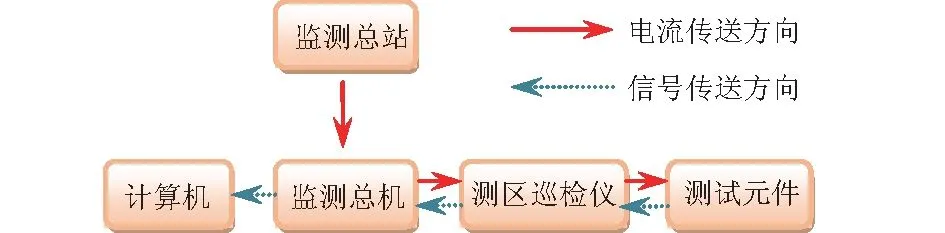
图6 测试系统信号传输示意图Fig.6 Signal transmission schemes of the test system

5 变形监测方案

立井井筒全深度范围内进行变形监测，不仅工作量大，而且经济投入多。因此，对于具体井筒的变形监测，可以通过水文地质情况以及井筒的结构特征，选择合适的监测断面进行重点监测，以达到施工简单、经济合理的要求。新巨龙煤矿所处地层中生界地层缺失，新生界与上古生界呈不整合接触，上古生界二叠系石千峰组地层总厚127.1 m，其中301.5～343.3 m为风化裂隙带，以下为完整基岩段。新生界第四系松散层为河床、河漫滩及浅水湖泊相交互沉积的松散沉积地层。因此，所选测区如下。

第1测区：距地表垂直深度280 m，新生界含水层与隔水层交界处；从地质柱状图可以看出，该区域位于新生界含水层以中细砂为主，其次为粗砂，夹多层灰绿色黏土及砂质黏土，北部富水性强。

第2测区：距地表垂直深度430 m底部含水层与基岩交界处；在井壁结构中位于大壁座位置。该区域主要有风化细砂岩、黏土质砂和风化泥岩组成。风化细砂岩颜色呈灰绿色，夹杂薄层泥岩，裂隙发育，裂隙面风化严重。风化泥岩呈深灰色，裂隙发育且较疏松。

第3测区：距地表垂直深度700 m，位于井筒马头门顶部；位于煤层编号25下煤底部，主要以泥岩、砂岩为主，局部为细、中、粗粒砂岩，岩石致密，裂隙不发育，属中等稳定岩层。

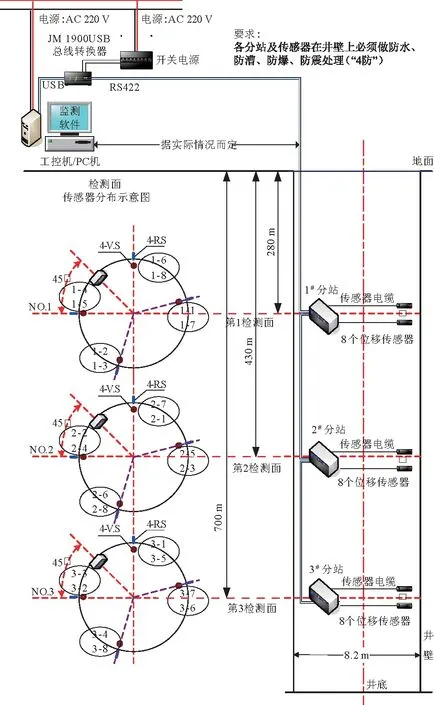
图7 新巨龙煤矿井筒测试系统布置Fig.7 Arrangement of shaft lining test system in Xinjulong coal mine

如图7所示，新巨龙煤矿井筒测试系统包括3个测试断面、12个水平位移传感器和12个垂直位移传感器，测试总站计算机安放在距离井筒70 m的井口电气设备控制机房。在筒壁上确定好8个传感器的安装位置，拟定为对称布置(若遇到管道等设施时，可适当调整)。

该监测系统在计算机的控制下，可以长期定时自动检测、存储测试数据，通过软件处理，自动显示或打印出井筒径向和纵向位移报表或变化曲线。地面测站人员可以通过计算机或报表研究井壁微小变形规律，及时分析并评估矿井井壁结构的安全性，同时还可以通过局域网实现报表、曲线及其有关井壁稳定性分析结果的数据共享。

6 变形监测结果及井壁强度校核

6.1 监测结果分析

新巨龙煤矿副井井筒变形监测系统在2014年11月份安装测试完成后，分时段对立井井筒的变形情况进行监测。为分析从测试系统安装以来到目前为止的井筒变形情况以及对监测系统的稳定性进行评价，将所采集的测试数据进行了汇总比较，并绘制3个不同深度的井壁纵向位移和径向位移变化曲线。

6.1.1 第1检测面(-280 m)

测试系统在选取的3个监测平面上取4个方位进行径向和纵向的位移监测。其中：编号为1，2，4，6的传感器为径向位移传感器；编号为3，5，7，8的传感器为纵向位移传感器(见图7)。第1检测面的变形监测结果如图8所示。图中初始日期为2014年11月20日。从图8中可以看出井筒径向变形最大值约0.48 mm，纵向变形最大值约1.5 mm，井壁变形在变形极限范围内。

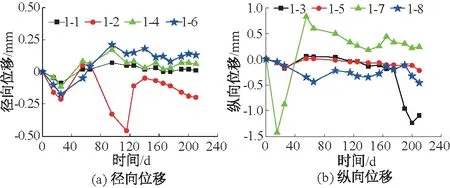
图8 第1测试断面(-280 m)径向位移和纵向位移Fig.8 Radial and longitudinal displacements of the first test section(-280 m)

6.1.2 第2检测面(-430 m)

本监测平面上取4个方位进行径向和纵向的位移监测。其中：编号为2，5，6，7的传感器为径向位移传感器；编号为1，3，4，8的传感器为纵向位移传感器(见图7)。第2检测面的变形监测结果如图9所示。从图9中可以看出井筒径向变形最大值约1.95 mm，纵向变形最大值约1.8 mm，此处井壁变形量最大，约为井壁变形极限值的82.5%，在此期间应密切关注井壁状态，加强监测。

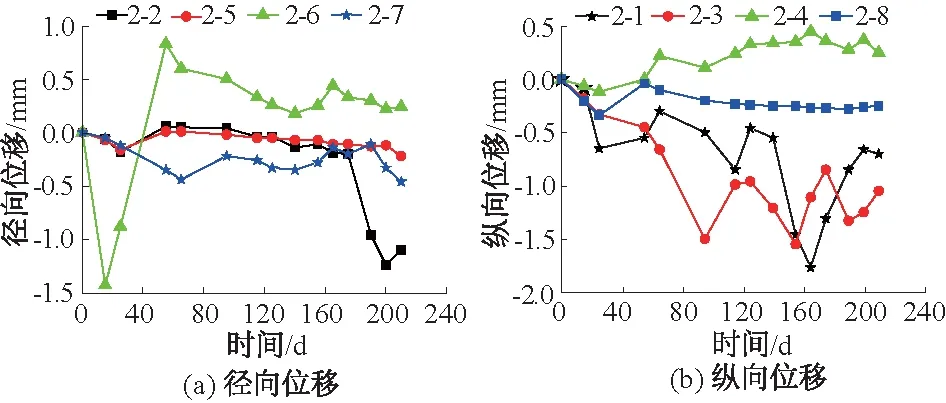
图9 第2测试断面(-430 m)径向位移和纵向位移Fig.9 Radial and longitudinal displacements of the second test section(-430 m)

6.1.3 第3检测面(-700 m)

本监测在选取的3个监测平面上取4个方位进行径向和纵向的位移监测。其中：编号为1，3，4，7的传感器为径向位移传感器；编号为2，5，6，8的传感器为纵向位移传感器(见图7)。第3检测面的变形监测结果如图10所示。从图10中可以看出井筒径向变形最大值约0.2 mm，纵向变形最大值约1.12 mm，井壁变形不大，此处井壁状态良好。

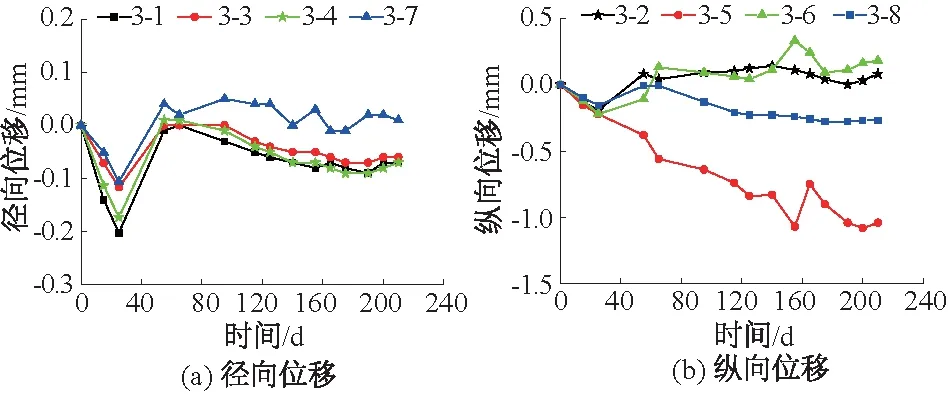
图10 第3测试断面(-700 m)径向位移和纵向位移Fig.10 Radial and longitudinal displacements of the third test section(-700 m)

综上分析，井壁变形属于弹性变形，增量在一定范围内波动，呈现非线性变化特征。从井壁变形曲线来看，井壁位移最大值出现在弱胶结地层底部含水层与基岩段交界处。井壁变形曲线在一段时间内出现峰值，这表明井壁存在潜在的破坏期，应对这个时期的井壁变形密切关注。因此，在井筒正常工作时，应加强分时段分区域的监测，做到主动防治，防患于未然。

6.2 井壁强度校核

井筒底部含水层与基岩段交界处井壁变形量最大，其中径向位移为1.95 mm。现对该位置井壁所受附加应力进行校核，根据式(3)有

31.15 MPa<σa=60 MPa 。

因此，该井壁尚未达到破裂极限状态，井壁处于弹性状态。研究表明：井筒的变形破坏是一个循序渐进的过程，通过对井筒的变形实时动态进行监测，根据变形量大小反演井筒的应力状态，可以有效地对井筒的安全状态进行合理评价。

7 结 论

(1) 弱胶结地层具有明显的分层性，立井井壁变形破坏最易发生在地层强度差异最大的位置。

(2) 根据双向受压混凝土强度破坏准则和厚壁圆筒空间轴对称问题位移解，得到了新巨龙煤矿井壁极限破坏状态下井筒内壁变形值为2.369 mm。

(3) 建立了多层位立井井筒变形智能监测系统，实现了弱胶结地层深井多点变形的预测预报。监测结果表明，井筒纵向变形最大值约1.8 mm，径向变形最大值约1.95 mm；在弱胶结地层底部含水层与基岩段交界处立井井壁变形量最大，约为井壁变形极限值的82.5%。

(4) 根据监测得到的变形量反演了井筒的应力状态，所得井壁最大变形位置的附加应力值小于井壁极限抗压强度，监测结果能够真实地反映井壁的受力状态，监测系统能够实现井壁安全状态的实时动态智能评估。

[1] 孙 闯，徐乃忠，刘义新，等. 基于双因素时间函数的松散地层条件下地表点动态沉降预计[J]. 岩土力学，2017，38(3)：821-826.

[2] 张文泉，董世卓，张贵彬，等. 巨厚新近系松散地层结构特征研究及其应用[J]. 煤炭技术，2016，35(4)：132-134.

[3] 李德海，许国胜，余华中. 厚松散层煤层开采地表动态移动变形特征研究[J]. 煤炭科学技术，2014，42(7)：103-106.

[4] 刘环宇，陈卫忠，王争鸣. 兖州矿区立井井筒破坏机制的理论分析[J]. 岩石力学与工程学报，2007，26(增1)：2620-2626.

[5] 张丁丁. 深厚松散层底部含水层渗流与变形试验研究[D]. 西安：西安科技大学，2013

[6] 张文泉，张永双，席京德，等. 煤矿立井井壁破裂的机制及防治措施[J]. 中国地质灾害与防治学报，2001，12(4)：13-17.

[7] 倪兴华，隋旺华，官云章，等. 我国煤矿立井井壁破裂概况[M]. 北京：中国矿业大学出版社，2005.

[8] 杨维好. 十年来中国冻结法凿井技术的发展与展望[C]∥中国煤炭学会成立五十周年高层学术论坛论文集. 北京：中国煤炭学会，2012：1-7.

[9] 刘环宇，李 晓，曾钱帮，等. 兖州矿区立井井筒非采动破裂的非线性预测与判别方法[J]. 工程地质学报，2005，13(2)：231-235.

[10] 刘环宇，王思敬，曾钱帮，等. 基于模糊神经网络兖州矿区立井井筒非采动破裂的判别[J]. 岩土工程学报，2005，27(10)：1237-1240.

[11] 邵良杉，张 宇. 煤矿立井井筒非采动破裂预测[J]. 煤炭学报，2009，34(2)：184-186.

[12] 袁志刚，王宏图，胡国忠，等. 立井井筒非采动破裂的遗传-支持向量机预测模型[J]. 煤炭学报，2011，36(3)：393-397.

[13] 张向东，韩云瑞，刘世君，等. 矿山立井井壁的变形预测模型[J]. 辽宁工程技术大学学报(自然科学版)，2014，33(8)：1070-1073.

[14] 许延春，高玉兵，李江华，等. 煤矿井筒安全状态评价体系改进及应用[J]. 煤炭科学技术，2016，44(10)：95-101.

[15] 陈祥福，申明亮，张 勇，等. 厚表土立井井壁破坏数值模拟研究[J]. 地下空间与工程学报，2010，6(5)：926-931.

[16] 王传武. 副井井筒的破坏机理和变形规律的研究[D]. 淮南：安徽理工大学，2015.

[17] 张 辉. 宿南矿区钱营孜煤矿井壁变形机理研究[D]. 徐州：中国矿业大学，2016.

[18] CHAI J，LIU J，QIU B，etal. Detecting Deformations in Uncompacted Strata by Fiber Bragg Grating Sensors Incorporated into GFRP[J]. Tunneling and Underground Space Technology，2011，26(1)：92-99.

[19] 邱 标. 基于光纤光栅监测的厚松散层井筒变形预测研究[D]. 西安：西安科技大学，2009.

[20] 刘化宽. 基于光纤光栅技术的立井井筒变形监测预警方法及系统研究[D]. 北京：北京交通大学，2014.

[21] 黄明利，吴 彪，刘化宽，等. 基于光纤光栅技术的井壁监测预警系统研究[J]. 土木工程学报，2015，48(增1)：424-428.

[22] 王渭明，陈正大，徐乐年，等. 深立井多层位自动监测研究与应用[J]. 岩土力学，2003，24(增2)：384-387,391.

[23] 梁恒昌，周国庆，赵光思，等. 井壁破裂过程的应变实测特征分析[J]. 煤炭学报，2010，35(2)：198-202.

[24] 陈晓祥，杨维好. 新型单层冻结井壁水平极限承载特性试验研究[J]. 岩石力学与工程学报，2013，32(增2)：3740-3748.

[25] 张治国，徐 晨，宫剑飞. 隧道开挖对邻近桩基变形及承载能力影响的弹塑性解答[J]. 岩石力学与工程学报，2017，36(1)：208-222.

[26]BARTON N. Shear Strengthcriteria for Rock, Rock Joints, Rockfill and Rock Masses: Problems and Some Solutions[J]. Journal of Rock Mechanics and Geotechnical Engineering，2013，5(4)：249-261.

[27] 李文婷，李树忱，冯现大，等. 基于莫尔-库仑准则的岩石峰后应变软化力学行为研究[J]. 岩石力学与工程学报，2011，30(7)：1460-1466.

[28] 许延春. 深部饱和黏土的力学性质特征[J]. 煤炭学报，2004，29(1)：26-30.

[29] 孟志强，纪洪广，彭 飞. 冻结法成井井壁在深厚表土段附加应力研究[J]. 煤炭学报，2013，38(2)：204-208.

[30] 周 扬，周国庆. 塑料板夹层双层井壁的轴对称变形分析[J]. 煤炭学报，2010，35(9)：1470-1475.

[31] 周 扬，周国庆，梁化强. 井壁约束内壁治理方法的力学分析[J]. 中国矿业大学学报，2009，38(2)：197-202.

[32] 刘环宇. 厚冲积层立井井筒破坏的发生机理及防治技术研究[D]. 南京：河海大学，2005.

[33]梁亚平, 王惠珍, 任兴民. 两端均布、轴向线性分布压力作用下厚壁圆筒空间轴对称问题的解析解[J]. 中国科学:物理学 力学 天文学, 2007, 37(5):684-688.

[34]贾海宾. 厚表土层立井井筒非采动变形破坏分析与预测[D]. 青岛：山东科技大学，2012.