岩样单裂隙几何参数对其破坏模式与强度的影响
, ,2
(1.中南大学 资源与安全工程学院,长沙 410083;2.河南理工大学 河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地,河南 焦作 454000)
1 研究背景
在大量的工程建设中,不可避免地会遇到一系列的岩石材料,由于长期的地质作用,这些材料往往含有大量断层、节理和裂隙等不连续面,这些不连续面对岩体的力学性能有着重要的影响。为了深入地了解裂隙岩体的力学特征,国内外学者[1-14]对裂隙进行各种简化、分类,其中含单裂隙岩体作为裂隙岩体研究的基础,有众多学者[1-11]对其有过研究。目前,对含单裂隙岩体的研究主要是通过对真实裂隙岩体试样或类岩材料试样进行加载以及采用数值模拟等方法来进行。Lee等[1]利用不同材料的含单双裂隙的岩体进行了一系列单轴压缩试验,发现了不同材料试样中的裂隙扩展、贯通模式差异及试样的起裂应力、峰值应力等变化规律。林鹏等[2]通过对含预制单裂隙的花岗岩试样进行试验研究,发现裂隙倾角对裂纹的扩展和最后的破坏行为有较大的影响。黄达等[3]利用PFC2D对单裂隙砂岩单轴压缩的应变率效应进行探究,试验中观察到裂纹首先在裂隙尖端出现,起裂形式为Ⅰ型翼裂纹,翼裂纹扩展一段长度后偏向岩样外侧,大致沿裂隙倾角方向拉剪复合贯通;还发现裂隙的扩展模式与裂隙倾角及加载速率有关。顾成富等[4]运用岩石破裂失稳软件RFPA2D对含单裂隙岩样进行了模拟试验,研究了裂隙的分布位置及走向对岩石试件破裂过程的影响。蒋明镜等[5]通过含裂隙岩体的离散元数值分析,研究了岩石裂纹的扩展与贯通机制。明华军等[6]通过颗粒离散元数值模拟试验,分析了裂隙张开度对岩样破坏过程和破坏模式的影响。Wang等[7]通过大理岩试样的单轴压缩试验和有限元数值模拟试验,发现了大理岩试样中裂隙尖端X型剪切裂纹的产生。Huang等[8]在含单裂隙大理岩试样的单轴压缩试验中发现加载过程中共有5种类型的裂纹产生。Wong等[9]对比分析了多位学者的试验结果,并通过自己对石膏和花岗岩试样的试验,对含单裂隙岩体的破坏模式进行了系统的研究;根据对高速摄像机记录的试验过程的分析,将加载过程中产生的裂纹分为7种类型,如图1所示。
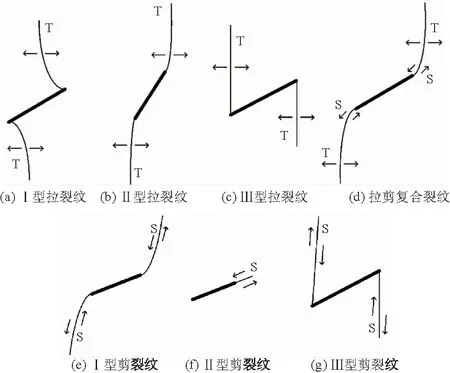
图1 萌生裂纹的7种类型Fig.1 Seven types of initiated cracks
以上研究多为单轴压缩作用下贯通型裂隙的试验,除此之外,还有很多三轴压缩、非贯通裂隙的研究。譬如:郭彦双等[10]采用含张开型表面裂隙的辉长岩试样,对单轴压缩条件下试样的破坏模式进行了一系列研究;肖桃李等[11]通过在类岩材料模型中预制相应的裂隙,研究了三轴压缩条件下试样的破坏特性。在含预制单裂隙试样的试验研究中,大部分是关于裂纹起裂、扩展及试样破坏等裂纹模式探究方面的,而对试样破坏强度的系统性研究较少。为此,本文利用FLAC3D建立相应模型,对多组含预制裂隙的试样进行单轴压缩试验,研究裂隙的几何参数对岩样破坏模式及强度的影响。
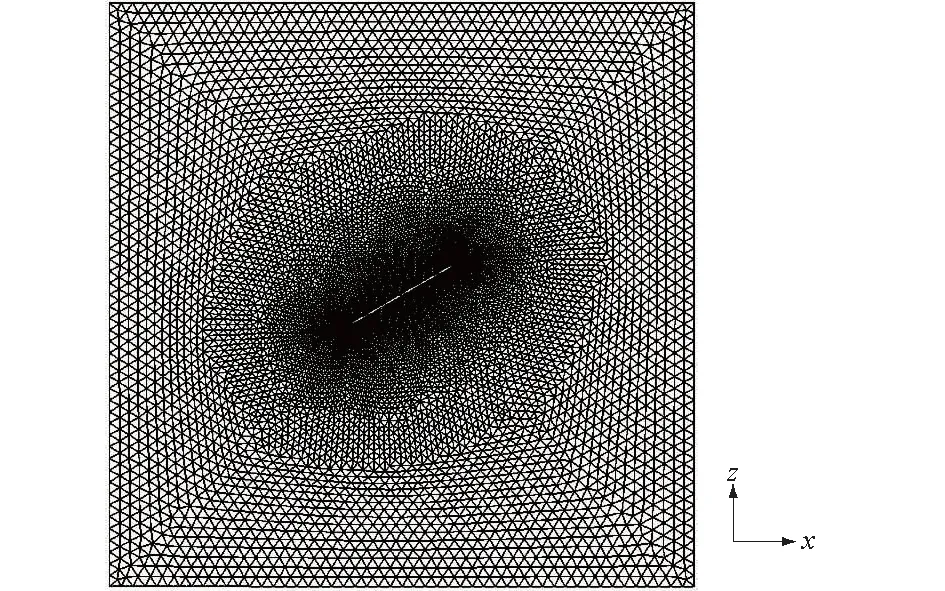
图3 划分网格后模型Fig.3 Mesh-divided model
2 试验模型及方案
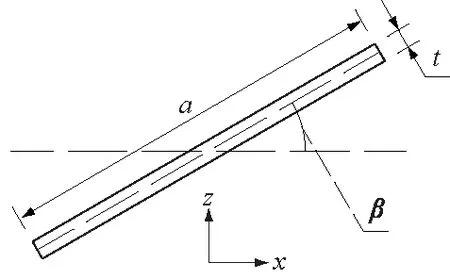
图2 模型平面图Fig.2 Plane figure ofmodel
为了研究单裂隙几何参数与试样破坏模式及强度之间的关系,本文建立如图2所示含单裂隙的试样模型。模型长和宽均为200 mm,考虑到计算时间问题,在y向取1 mm,即按平面应变问题考虑。其中a为裂隙长度,β为裂隙倾角(裂隙与水平方向的夹角),t为裂隙张开度(厚度)。
利用AutoCAD和ANSYS[15]建立相应的网格并划分模型,然后导入FLAC3D,最终得到的模型如图3。
试验沿z轴加载,并且在上下加载面施加z向约束;在模型前后表面施加y向约束,以保证平面应变条件。试样的材料模型采用FLAC3D中自带的应变软化模型。这是由于在加载过程中应变的增大导致岩石试样性能劣化,甚至产生裂纹,而这些过程可以通过应变软化模型里的参数设置来实现。例如,当岩样内产生裂纹时,裂纹面处的岩石是没有抗拉强度的,因此就可以设置当应变增大到一定值后,单元体的抗拉强度变为0,以此来模拟裂纹的产生。本文试样模型参数参考FLAC3D用户手册[16]。取值如表1,强度参数随塑性应变增大而变化的情况如表2。

表1 模型物理力学参数Table 1 Physical and mechanical properties of model
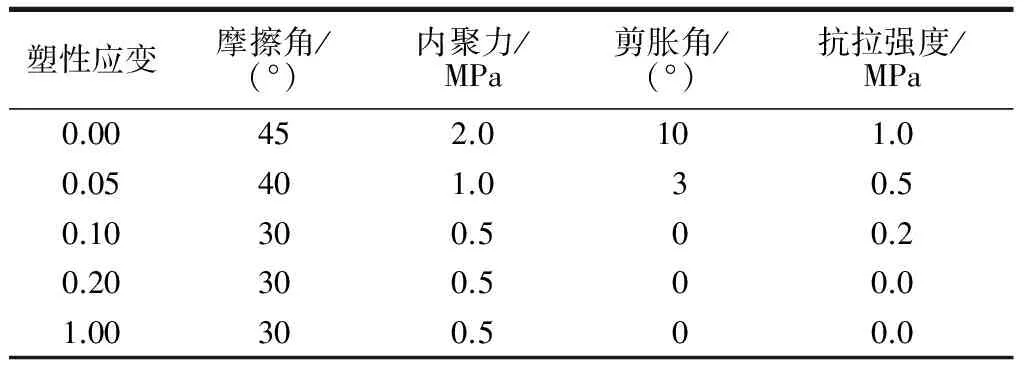
表2 强度参数变化Table 2 Changes of mechanical properties
针对3个不同的几何参数:裂隙长度(5,10,20,40,60,80 mm)、裂隙倾角(0°,15°,30°,45°,60°,75°,90°)、裂隙张开度(0.2,0.4,0.6,0.8,1.0,1.4,1.8 mm),设计以下6组试验方案:
(1)固定张开度不变为1.0 mm,以不同的倾角为系列,观察峰值应力随裂隙长度变化的规律。
(2)固定倾角不变为0°,以不同的张开度为系列,观察峰值应力随裂隙长度变化的规律。
(3)固定张开度不变为0.4 mm,以不同长度为系列,观察峰值应力随裂隙倾角变化的规律。
(4)固定长度不变为20 mm,以不同张开度为系列,观察峰值应力随裂隙倾角变化的规律。
(5)固定倾角不变为30°,以不同长度为系列,观察峰值应力随裂隙张开度变化的规律。
(6)固定长度不变为40 mm,以不同倾角为系列,观察峰值应力随裂隙张开度变化的规律。
3 裂隙倾角对单裂隙试样破坏模式的影响
从6组试验中抽取部分结果,分析裂隙倾角对单裂隙试样破坏模式的影响。其中裂隙长度为40 mm,裂隙张开度为0.2 mm。
3.1 裂隙倾角为0°
当预制裂隙倾角0°时,大约在0.27σc(σc为试样单轴抗压强度)左右,裂隙中部出现拉伸破坏单元,这是由于张开裂隙在压缩过程中,裂隙内表面处于受弯的状态,致使表面发生拉伸破坏。随着加载过程的进行,预制裂隙面上出现大量密集的拉伸破坏单元,越靠近中部相对越密集,并不断发育形成优势裂纹。继续加载至0.54σc左右时,如图4(a),中部的拉伸裂纹停止扩展,尖端处开始出现明显的剪切破坏单元,并不断增多进而形成剪切裂纹。在初始阶段,剪切裂纹从尖端向上下同时扩展,随着荷载的增加,裂隙右端上下都有剪切裂纹扩展,而左端只有向下的裂纹,并且由图4(b)可看出这些由尖端萌生出的裂纹在扩展过程中,并不是单一形式的,而是拉剪复合破坏。随后在裂隙右部尖端,于尖端上方距尖端一定距离处出现剪切区域并逐渐形成剪切裂纹,向内外同时扩展,特别是向内,则扩展至裂隙尖端。最后优势裂纹不断扩展至试样边界,如图4(c),进而达到峰值应力。

图4 裂隙倾角为0°时裂纹扩展过程Fig.4 Crack development with inclination angle 0°
3.2 裂隙倾角为15°
当裂隙倾角为15°时,在加载过程中,首先在尖端附近出现沿裂隙面的拉伸破坏单元。随着荷载不断增加,这些拉伸破坏不断发育,在距尖端一定距离处产生近乎垂直于预制裂隙面的拉伸裂纹并不断扩展,如图5(a),这也就是常见的拉伸翼裂纹。之后拉伸裂纹停止扩展,端部剪切裂纹开始萌生并不断扩展,如图5(b)。在剪切裂纹扩展过程中,伴随着一定量的拉伸破坏,最后形成近似“X型”的剪切裂纹,贯通岩样进而达到峰值应力,如图5(c)。

图5 裂隙倾角为15°时裂纹扩展过程Fig.5 Crack development with inclination angle 15°
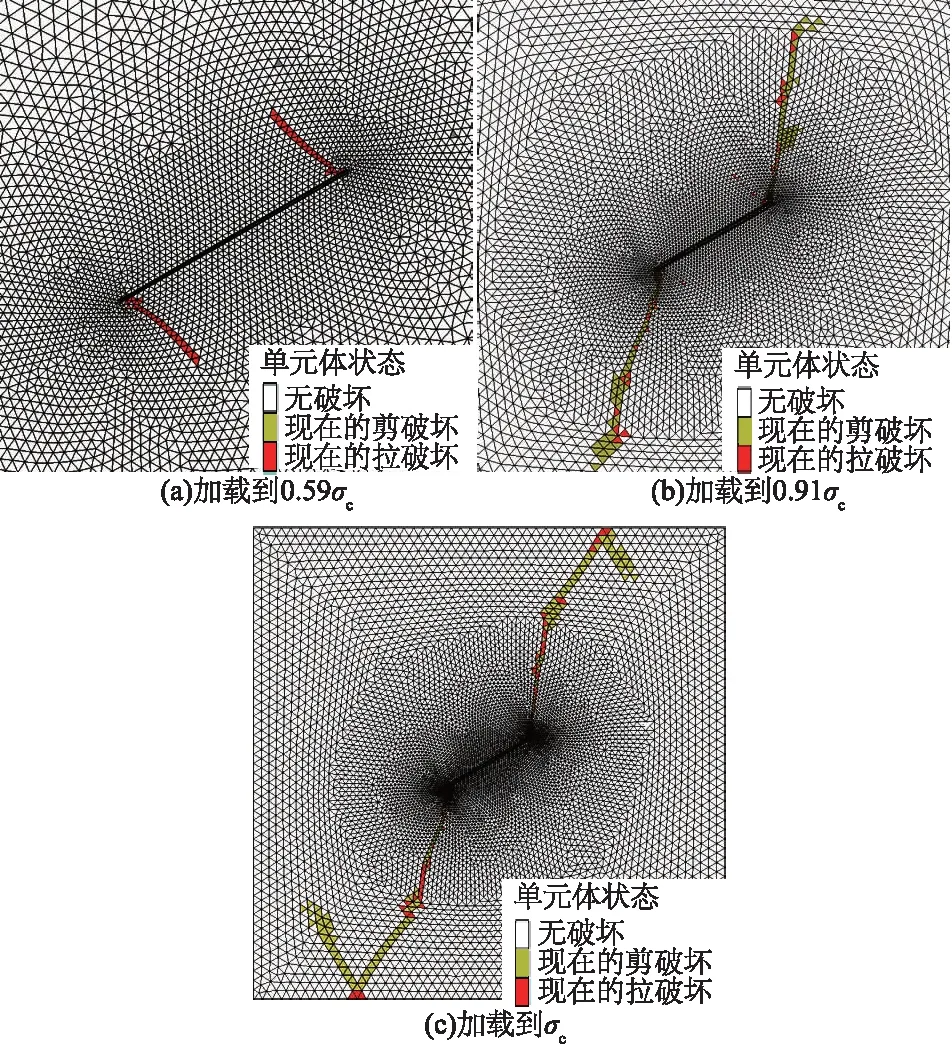
图6 裂隙倾角为30°时裂纹扩展过程Fig.6 Crack development with inclination angle 30°
3.3 裂隙倾角为30°,45°
当裂隙倾角为30°和45°时,试样的破坏模式基本一致。加载到0.2σc左右时,裂隙端部附近出现拉伸破坏单元,并不断发育为拉伸翼裂纹。翼裂纹刚开始与预制裂隙几乎垂直,随着荷载增加,逐渐偏向最大主应力的方向,如图6和图7。
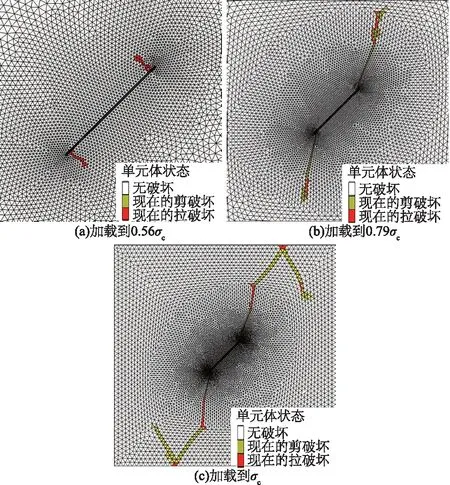
图7 裂隙倾角为45°时裂纹扩展过程Fig.7 Crack development with inclination angle 45°
在翼裂纹扩展过程中,端部剪切破坏单元逐渐增多,并不断发育,形成Ⅰ型剪切裂纹(即文献[9]中提到的7种裂纹之一,下文中裂纹名称都参照文献[9])。最后剪切裂纹扩展并贯通岩样,进而达到峰值应力。两者不同的是,当裂隙倾角为45°时拉伸翼裂纹扩展长度相对较短。

图8 裂隙倾角为60°时裂纹扩展过程Fig.8 Crack development with inclination angle 60°
3.4 裂隙倾角为60°
当裂隙倾角为60°时,加载到大概0.14σc时,首先在裂隙尖端出现剪切破坏单元。然后端部出现拉伸单元,随后近似出现很短的拉伸翼裂纹,如图8(a)。
然后在端部随即开始萌生出Ⅰ型剪切裂纹,剪切裂纹扩展的同时,伴随少量的拉伸破坏单元。加载到0.89σc左右,逐步出现 Ⅱ 型和 Ⅲ 型剪切裂纹,如图8(b),但之后的过程中,下部尖端处的 Ⅰ 型裂纹向外发生偏折,和Ⅱ型裂纹汇聚,共同向下扩展,与Ⅲ型裂纹一起形成“X型”剪切破坏。之后整个裂纹贯通,试样破坏,进而达到峰值应力,如图8(c)。
3.5 裂隙倾角为75°
当裂隙倾角为75°时, 起裂应力变得较大, 加载到0.19σc左右时, 首先在尖端出现拉伸破坏单元, 紧接着尖端又产生剪切破坏。 但是在接下来的一段时间内, 裂隙尖端并没有形成相对宏观的裂纹破坏, 没有观察到拉伸翼裂纹的产生。 直到0.68σc左右时, 尖端的剪切单元增多并相互贯通, 萌生形成整体的裂纹, 主要形式为Ⅱ型和Ⅲ型剪切裂纹, 如图9(a)。 随着加载的不断进行, Ⅲ型裂纹没有继续扩展, 而主要以Ⅱ型剪切裂纹的方式(如图9(b))不断向试样边界扩展, 最终达到峰值应力, 如图9(c)。
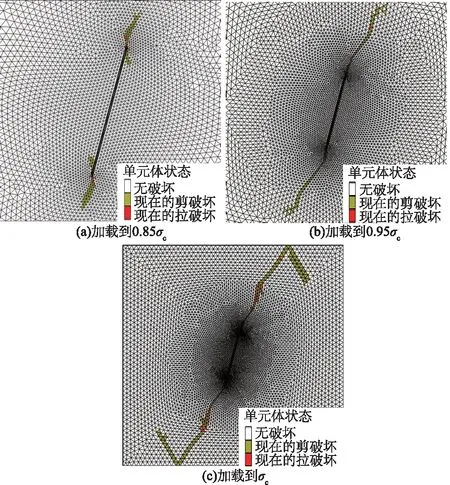
图9 裂隙倾角为75°时裂纹扩展过程Fig.9 Crack development with inclination angle 75°
3.6 裂隙倾角为90°
当裂隙倾角为90°时,其起裂应力急剧增大,比其他角度情况下的峰值应力还要高,加载到0.9σc左右时,第一次在尖端附近出现剪切破坏单元。随后并没有像常见的那样沿加载方向发生张拉劈裂破坏,而是在裂隙两侧迅速出现剪切破坏区域并扩展至裂隙尖端,在裂隙周围形成菱形核状区域,如图10(a)。同时试样两侧边界处出现剪切带,并逐渐向中心区域扩展,如图10(b),此时试样已经达到峰值应力。接下来以中部菱形剪切区域为中心,逐渐向四周以剪切破坏形式不断扩展,这个过程中,应力迅速跌落,试样表现出明显的脆性,最后试样呈现出整体性的“X型”剪切破坏,如图10(c)(此时达到残余强度σr)。
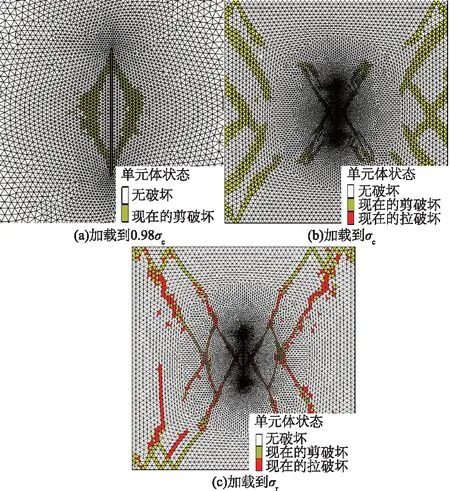
图10 裂隙倾角为90°时裂纹扩展过程Fig.10 Crack development with inclination angle 90°
3.7 不含裂隙的完整试样
对于不含裂隙的完整试样,加载到0.97σc左右,在试样边界处首先出现剪切破坏单元。然后与90°相似,在试样左右两侧边界处出现剪切区域,如图11(a),并逐渐形成优势裂纹,此时试样已经达到峰值应力。此后,裂纹不断由边界向中心区域失稳扩展,应力迅速跌落。与90°裂隙试样相比,峰值应力几乎一样,而在破坏模式上,稍有差异,但是大致都呈现出相似的X型破坏(如图11(b) 、图11(c))。
另外在大部分试验中,裂纹贯通试样后,并没有立即完全达到峰值应力,而是发生向试样两侧的弯折,在端部发生“破坏”。这一现象与Lee等[1]的模拟结果较为类似,如图12。这些“裂纹”在前人研究成果[1,17-18]中被称作“White Patch”或“White Belts”,这些“裂纹”是由于在荷载作用下,岩样本身内部的微裂纹不断发育的外在表现。随着荷载增加,这些白带并不会绝对形成肉眼可见的宏观裂纹。
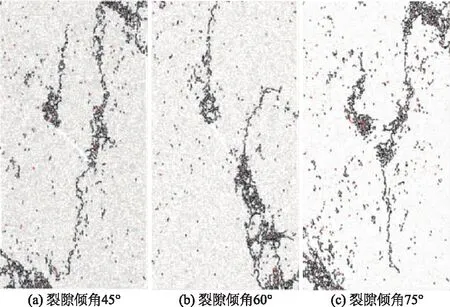
图12 文献[1]中PFC模拟结果Fig.12 PFC simulation results in Reference [1]
综合上述8个试样的裂纹生成、扩展、贯通过程,与前人的研究结果[1-4,7-9]基本类似——常见的拉伸翼裂纹其扩展长度是有限的,并不会导致试样破坏,真正导致试样破坏的是后期的剪切裂纹或拉剪复合型裂纹,其中主要形式表现为Ⅰ型剪切裂纹或Ⅰ型、Ⅲ型共同形成的“X型”剪切裂纹。并且随着角度增大(15°~75°),拉伸翼裂纹的长度不断变小。此外拉伸翼裂纹的生成并不一定在裂隙尖端,譬如在裂隙倾角为15°时,如图5(a),翼裂纹从距尖端一定距离处出现,随着裂隙倾角的增大,翼裂纹出现位置逐渐向尖端靠近。因此可验证本文结果的有效性。
其次,在试验过程中还得到了上述试样加载的应力-位移曲线,如图13。与岩石单轴压缩的强度-位移曲线类似,有明显的压密段、弹性段、裂纹稳定扩展段、裂纹不稳定扩展阶段和峰后残余段。且由图13可知裂隙倾角较小的试样,峰值应力较小,同时峰后表现出明显的延性。随着裂隙倾角的增大,试样的峰值应力不断增大,同时试样的脆性也越明显,在峰后产生更大的应力降落。并且由加载曲线可以更加直观地看到,裂隙倾角为90°的试样与不含裂隙的完整试样的加载曲线几乎完全重合,这再次说明了两者破坏模式的一致性,说明当裂隙倾角为90°时,裂隙对试样的影响较小。

图13 应力-位移曲线Fig.13 Curves of stress versus displacement
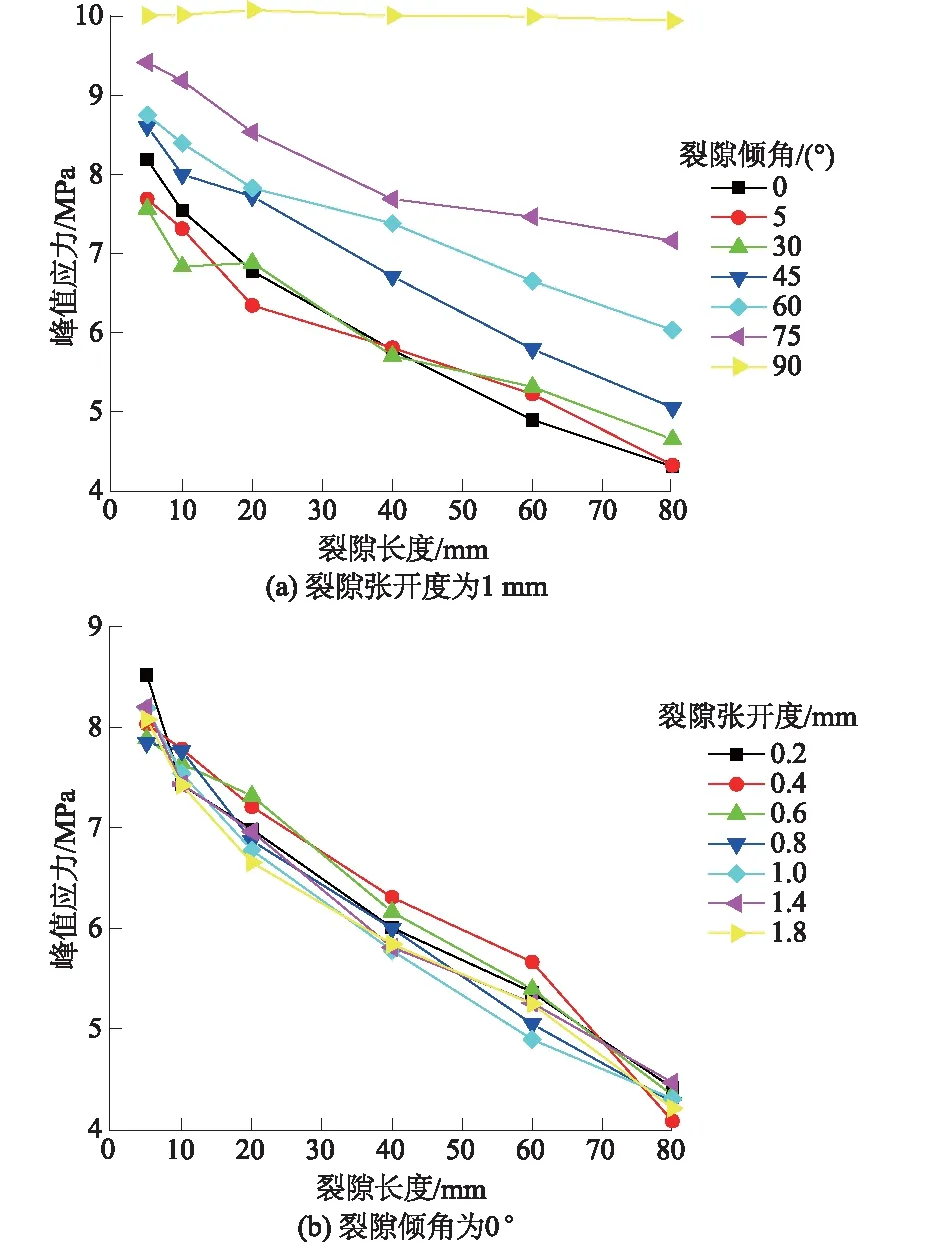
图14 单裂隙岩体峰值应力随裂隙长度的变化Fig.14 Curves of peak stress versus flaw length for single-flawed rock
4 裂隙几何参数对岩样单轴抗压强度的影响
4.1 预制裂隙长度对岩样峰值应力的影响
由图14(a)可以看出,当张开度固定时,除了90°试样,含裂隙岩体的单轴抗压强度整体上随着裂隙长度的增大而减小。当裂隙倾角为90°时,随裂隙长度增大,岩体的强度基本保持不变,此时试样强度与完整试样强度接近,在小范围波动;通过纵向比较可知,当裂隙倾角较小时,试样峰值应力变化不大,而当裂隙倾角>30°时,峰值应力呈现明显的增大,这可能与破坏模式有关。因为几乎所有试样都是由剪切破坏或拉剪复合破坏导致最终的破坏,但是在末期剪切带形成前,小角度试样中都会有明显的翼裂纹产生,这一定程度上可以等效为给试样增加了初始的缺陷,而当裂隙倾角>30°时,随着裂隙倾角的增大,翼裂纹不断变短,甚至消失,从而导致了峰值应力的增大。另外由图14(a)可以看出,裂隙角度越小,试样峰值应力随长度增大而减小的量越大。当角度固定时,如图14(b),随着裂隙长度的增大,试样峰值应力仍然呈递减趋势。同时通过纵向对比发现,不同的张开度对试样的峰值应力的影响不大。
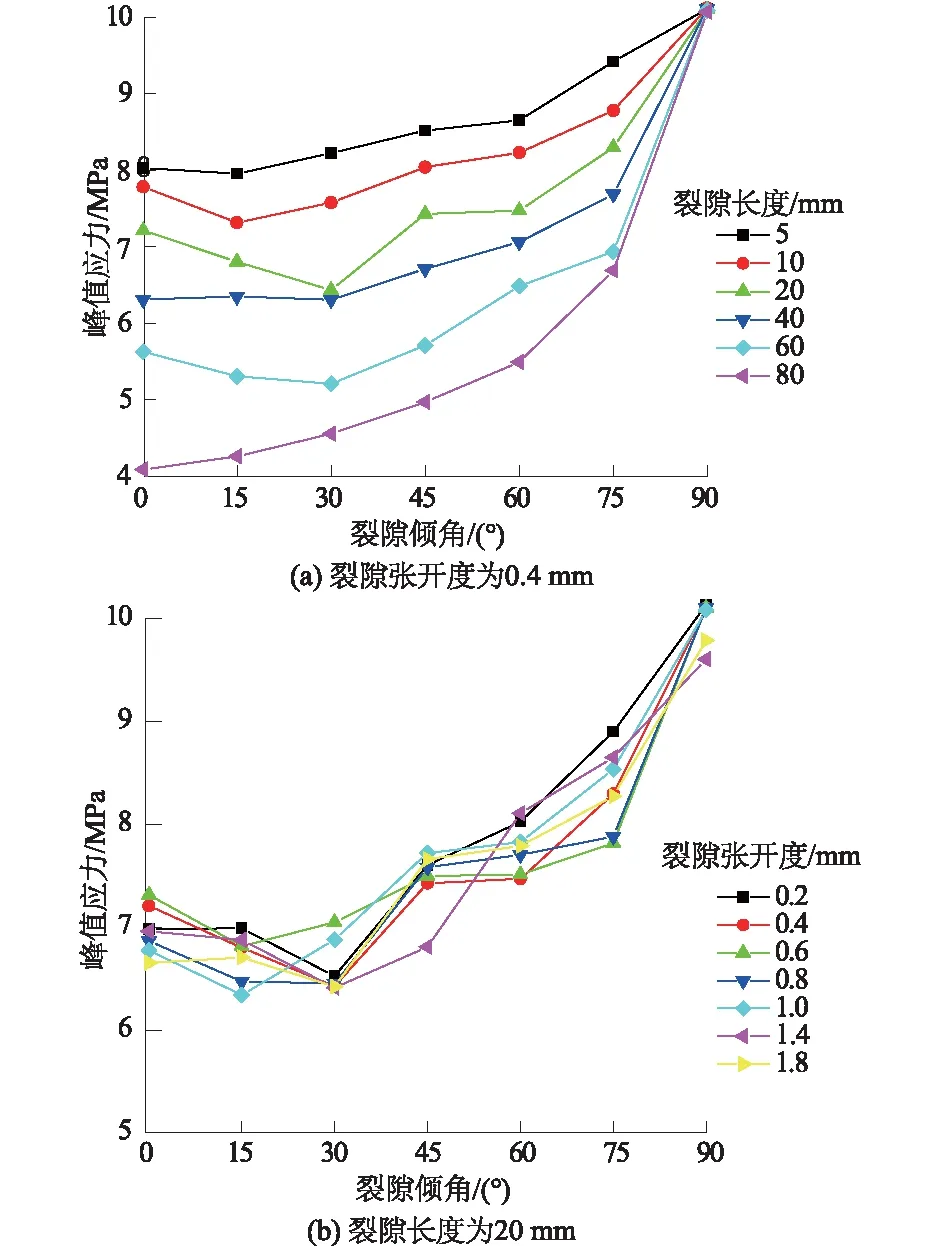
图15 单裂隙岩体峰值应力随裂隙倾角的变化Fig.15 Curves of peak stress versus flaw inclination angle for single-flawed rock
4.2 预制裂隙倾角对岩样峰值应力的影响
由图15(a)可以看出:当张开度固定不变时,随着裂隙倾角的增大,试样峰值应力整体上呈增大趋势且长度越大,峰值应力的变化量越大,也就是说,裂隙的长度越小,对试样强度的影响越小。当裂隙倾角较小时(<60°),试样峰值应力变化较小。当裂隙倾角较大时,试样峰值应力增长迅速,特别是当裂隙长度越长时,这一点表现得越明显。另外通过纵向对比,再一次反映了随着裂隙长度的增大,峰值应力不断减小的规律,以及当裂隙倾角为90°时,峰值应力几乎与裂隙长度无关的事实。而当裂隙长度固定时(图15(b)),与图15(a)相比,峰值应力随倾角变化的整体趋势没有太大差别——随着裂隙倾角的增大,试样的峰值应力呈增大趋势。倾角较大时峰值应力增长速率较快,而当倾角较小时,峰值应力增长缓慢,并且在15°~30°时,会出现应力的跌落现象。
图16为Lee等[1]对含单裂隙大理岩试样单轴压缩试验结果,观察其中含单裂隙岩样的峰值应力曲线,也就是圆圈代表的数据点所拟合得到的实线。与图15中结果相比,两者有较好的一致性,即在倾角较小时应力变化缓慢,在倾角较大时,应力增长比较迅速。
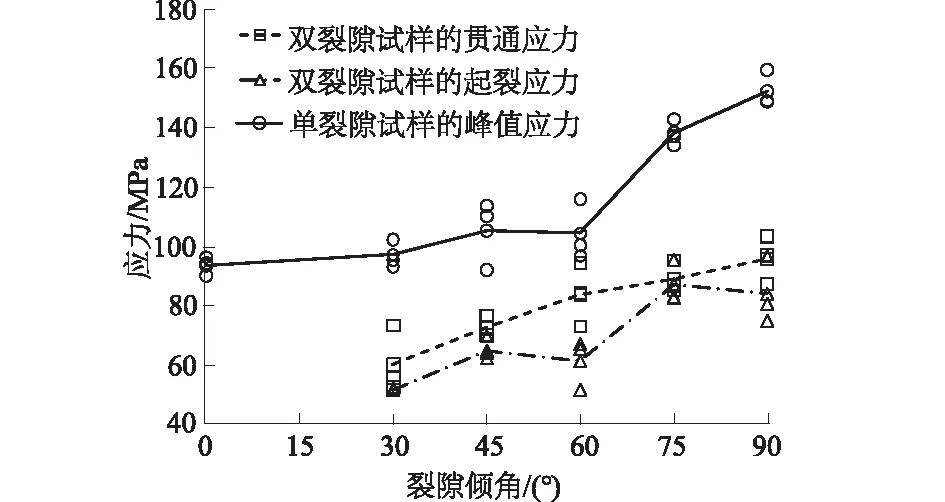
图16 Lee等[1]对含单裂隙花岗岩试样单轴压缩试验结果Fig.16 Result of uniaxial compression test on granite specimen containing single flaw by Heekwang Lee[1]
4.3 预制裂隙张开度对岩样峰值应力的影响
由图17可看出,随着裂隙张开度的变化,岩样峰值应力整体上基本保持不变,在小范围内呈无规律波动。明华军等[6]在研究带裂隙岩体的破坏模式时发现,岩体中的预制裂隙存在着极限相对裂隙张开度,当裂隙张开度小于这个极限值时,岩石受力作用占主导地位,而裂隙的影响较小。对于图17(b),相对裂隙张开度(裂隙张开度/裂隙长度)变化范围为0.005~0.045。由于本次试验试样数量有限,可能使其相对张开度均小于相应的极限值,因此出现试样峰值应力随张开度变化而基本不变的现象。而在图17(a)中,当裂隙长度为5 mm时,即使最大相对裂隙张开度达到0.36(张开度为1.8 mm),相对来说曲线依然变化不大,这是由于此时裂隙长度本来就很小,导致裂隙其他因素对试样的影响也会减小,这也正说明了含裂隙岩体的强度是受裂隙各项几何参数综合影响的,而并非单一因素的作用。另外通过纵向对比,再次验证了4.1节和4.2节所反映的规律——裂隙长度越大,试样的峰值应力越小;裂隙倾角越大,试样峰值应力越大,且倾角越大,峰值应力的增长率越大。
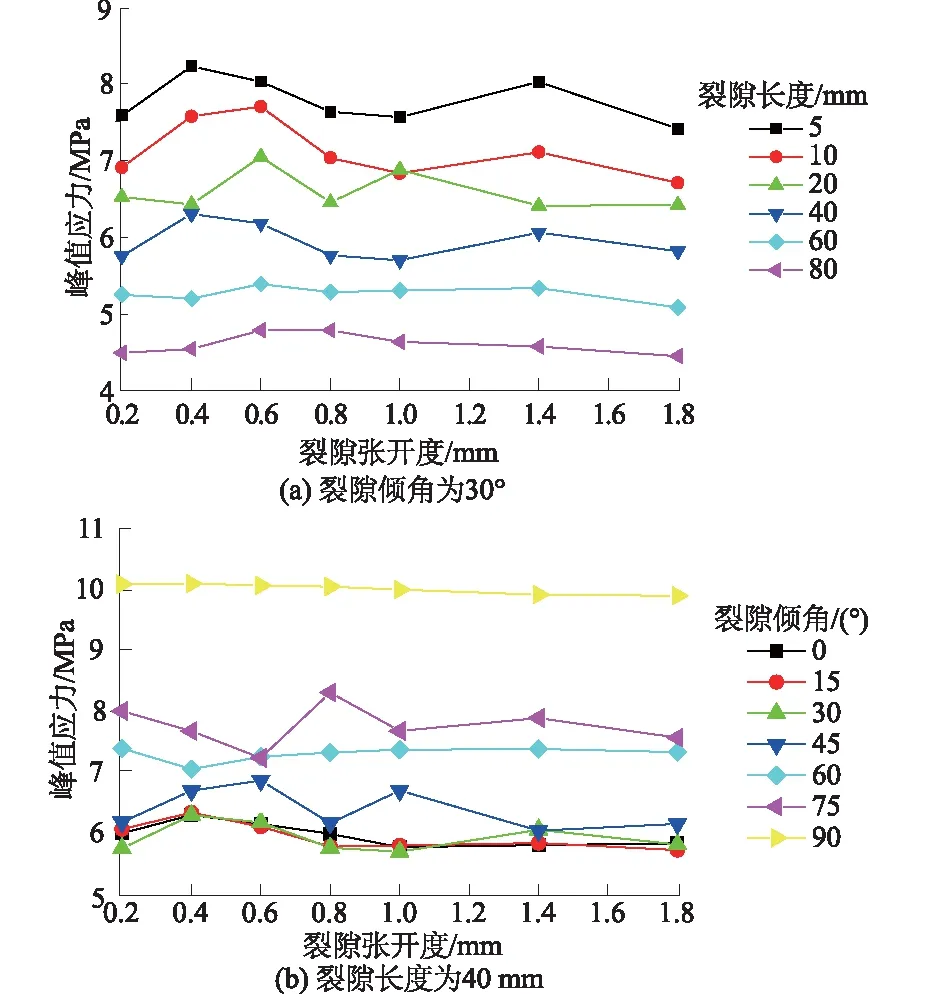
图17 单裂隙岩体峰值应力随裂隙张开度的变化Fig.17 Curves of peak stress versus flaw thickness for single-flawed rock
5 结 论
本文采用FLAC3D建立含单裂隙的试样模型,然后通过改变单裂隙的几何参数,开展单轴压缩试验研究。通过对试验结果的对比分析,得到如下结论。
(1)在含单裂隙试样的单轴压缩过程中,首先在尖端附近出现拉伸翼裂纹,且其萌生位置并不一定都在裂隙尖端,而是从距尖端一定距离处生成,随着裂隙倾角增大,翼裂纹长度逐渐变短,生成位置不断向尖端靠近。
(2)翼裂纹扩展长度有限,并不会导致试样破坏。随着加载进行,逐渐由尖端萌生出不同类型的剪切裂纹,并导致试样的最终破坏。
(3)裂隙倾角越大,试样的脆性越明显。随着裂隙长度的增大,试样峰值应力不断降低;随着裂隙倾角的增大,试样峰值应力整体上不断增大。但当倾角较小时,峰值应力增长十分缓慢,当倾角较大(>60°)时,峰值应力迅速增大;随着裂隙张开度的增大,在试验范围内,试样峰值应力基本保持不变。
[1] LEE H, JEON S. An Experimental and Numerical Study of Fracture Coalescence in Pre-cracked Specimens under Uniaxial Compression[J]. International Journal of Solids and Structures, 2011, 48(6):979-999.
[2] 林 鹏,黄凯珠,王仁坤,等.不同角度单裂纹缺陷试样的裂纹扩展与破坏行为[J].岩石力学与工程学报,2005,24(增2):5652-5657.
[3] 黄 达,岑夺丰,黄润秋.单裂隙砂岩单轴压缩的中等应变率效应颗粒流模拟[J].岩土力学,2013,34(2):535-545.
[4] 顾成富,王 辉.压应力作用不同裂纹分布下岩石破坏过程的数值模拟[J].煤炭技术,2015,34(5):108-110.
[5] 蒋明镜,陈 贺.岩石裂纹扩展与贯通机制的离散元数值分析[C]∥颗粒材料计算力学研究进展.大连:大连理工大学出版社,2012:326-337.
[6] 明华军,徐小峰,梁 波.不同裂隙张开度下岩石材料破坏的颗粒离散元模拟[J].三峡大学学报(自然科学版),2013,35(6):63-66.
[7] WANG R, ZHAO Y, CHEN Y,etal. Experiment and Finite Element Simulation of X-type Shear Fractures from a Crack in Marble[J]. Tectonophysics,1987,144(1/3):141-150.
[8] HUANG J, CHEN G, ZHAO Y,etal. An Experimental Study of the Strain Field Development Prior to Failure of a Marble Plate under Compression[J]. Tectonophysics, 1990, 175(1/3):269-284.
[9] WONG L N Y, EINSTEIN H H. Systematic Evaluation of Cracking Behavior in Specimens Containing Single Flaws under Uniaxial Compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2):239-249.
[10] 郭彦双,黄凯珠,朱维申,等.辉长岩中张开型表面裂隙破裂模式研究[J].岩石力学与工程学报,2007,26(3):525-531.
[11] 肖桃李,李新平,郭运华.三轴压缩条件下单裂隙岩石的破坏特性研究[J].岩土力学,2012,33(11):3251-3256.
[12] 黄彦华,杨圣奇.非共面双裂隙红砂岩宏细观力学行为颗粒流模拟[J].岩石力学与工程学报,2014,33(8):1644-1653.
[13] 杨圣奇,黄彦华,刘相如.断续双裂隙岩石抗拉强度与裂纹扩展颗粒流分析[J].中国矿业大学学报,2014,43(2):220-226.
[14] 杨圣奇,蒋昱州,温 森.两条断续预制裂纹粗晶大理岩强度参数的研究[J].工程力学,2008,25(12):127-134.
[15] 龚曙光.ANSYS参数化编程与命令手册[M].北京:机械工业出版社, 2009.
[16] Itasca Consulting Group. Fast Lagrangian Analysis of Continua in 3 Dimensions,User Manual,Version 3.1[M]. Minneapolis,Minnesota:Itasca Consulting Group, Inc, 2004.
[17] WONG L N Y, EINSTEIN H H. Crack Coalescence in Molded Gypsum and Carrara Marble: Part 2—Microscopic Observations and Interpretation[J]. Rock Mechanics and Rock Engineering, 2009, 42(3): 513-545.
[18] LI Y P, CHEN L Z, WANG Y H. Experimental Research on Pre-cracked Marble under Compression[J]. International Journal of Solids and Structures, 2005, 42(9/10): 2505-2516.

