钻孔孔壁切缝解除地应力测试方法数值模拟研究及工程应用

， ，，

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010；2.西藏自治区水利电力规划勘测设计研究院，拉萨 850000； 3.上海勘测设计研究院有限公司，上海 200434)

1 研究背景

作为岩体的赋存环境之一，地应力的大小和方位直接关系到长大隧道、地下洞室等工程布置和安全， 因此对重要工程部位地应力进行精细测试分析成为亟待研究与解决的关键技术问题。进行现场地应力实测是研究地应力的最直接的方法。国际岩石力学委员会(ISRM)[1]建议的试验方法主要有：钻孔孔径变形测量法、钻孔孔壁应变测量法、水压致裂法和应力恢复测量法。其中，钻孔孔壁应变测量法一次测量就能得到测试部位岩体的全应力张量[2-4]，水压致裂法具有操作简单、测量深度大和资料整理不受岩体力学参数影响等优点[5-6]。因此，以上2种方法在工程实际中应用较为普遍。

目前，在建及待建的西部水利水电工程大都具有埋深大、高地应力及构造复杂等特点。然而在极高应力环境中，常规的钻孔孔壁应变解除测量法在取芯过程中岩芯饼化现象的产生易造成试验失败，水压致裂法试验过程中则需要超高压设备而加剧试验难度，因此高应力环境中的地应力测量成为一大难题。国内专家葛修润等[7]对地应力测试设备进行了改进，提出了钻孔局部壁面应力全解除法；艾凯等[8]提出了基于部分恢复变形的洞壁切缝解除法来测量高应力条件下洞室开挖面岩体表面应力，在此基础上，刘允芳等[9]拓宽应用它的试验成果，得到了围岩的弹性模量。长江科学院在国内首次引进钻孔孔壁切缝解除法[10]，通过现场试验证明该方法适合高应力区岩体应力测量。

本文采用有限元对钻孔孔壁切缝应力解除过程进行数值模拟，通过计算研究试验时达到的使应力完全释放的最小切缝深度，并模拟计算了不同应力边界条件下切缝深度对切缝上部观测点应变及对孔周和孔径方向的影响，以优化试验过程中切缝的布置方案。根据数值模拟结果得到试验布置方案，将该方法用于处于极高应力条件下的锦屏地下实验室的应力测试中。

2 钻孔孔壁切缝解除前后应力状态

2.1 测试方法简介

钻孔孔壁切缝法地应力测试是一种基于原位应力释放原理的应力测量方式，其测试装置示意图见图1。借助如图1所示的由空压机驱动的小型金刚石锯片，在钻孔孔壁上切割出若干条围绕钻孔圆心按一定角度分布的平行于钻孔轴线方向的切缝，使切缝两侧表面法向应力完全释放。通过测读切缝一侧岩体表面由应力释放前后的法向应变变化值，根据弹性理论计算出岩体应力状况。

图1 测试设备构造Fig.1 Structure of test equipment

钻孔孔壁切缝法地应力测试结果精度取决于测试部位岩体的刚度以及应变传感器的灵敏度。正常情况下应变传感器的分辨率约为10-6，当岩体弹性模量为40 GPa时，地应力测试精度可以达到±0.5 MPa。

2.2 切缝前孔壁应力、应变状态

将岩体视为各向同性的线弹性体，钻孔坐标系如图2所示，其中z轴平行于钻孔轴向。定义原岩应力分量为Sxx，Syy，Szz，Sxy，Syz，Szx，则钻孔后，图1中孔壁上与x轴夹角为θ部位的应力为：

σθθ=Syy[1-2cos(2θ)]]+Sxx[1+cos(2θ)]]-

Sxysin(2θ) ;

(1)

σzz=Szz+2μ[-Syycos(2θ)+Sxxcos(2θ)]-

2Sxycos(2θ)]];

(2)

σθz=2Syzcosθ-2Syzsinθ;

(3)

σrr=σrθ=σrz=0 。

(4)

式中：σθθ为孔壁上切向应力分量；σzz为孔壁上轴向应力分量；σrr为孔壁上径向应力分量；σθz，σrθ，σrz为各剪应力分量；μ为泊松比。

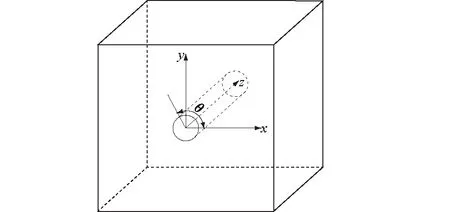
图2 钻孔坐标系Fig.2 Coordinate system of borehole

根据胡克定律，钻孔孔壁的切向应变εθ、轴向应变εz及剪应变γzθ分别为：

4(1-μ2)Sxysin(2θ)-μSzz] ;

(5)

(6)

(7)

式中E为岩石的弹性模量。假定切缝法向平面即钻孔横截面应力状态满足平面应变条件，则孔壁上切向应变εθθ为

εθθ=(1/E)[σθθ-μ(σrθ+σrr)] 。

(8)

2.3 切缝解除后切缝法向应力、应变状态

在进行现场钻孔孔壁切缝应力解除试验时，切缝平行于钻孔轴向，因此，钻孔孔壁的切向应力和切向应变即为切缝的法向应力和法向应变。

试验过程中，随着切缝深度的增加，切缝法向应力逐渐释放，如果定义应力释放率为ρ，当ρ=1时，应力完全释放，则切缝解除引起的切缝法向应力和法向应变改变量分别为：

Δσθθ=ρ[Syy(1-2cos2θ)+]

Sxx(1+cos2θ)-Sxysin2θ] ;

(9)

(10)

由式(4)可知σrr=σrθ=0，现场钻孔孔壁切缝解除法试验观测值为法向应变改变量，因此，法向应变改变量Δεθθ为应力释放率ρ及法向应力改变量Δσθθ的函数。岩石的弹性模量E和泊松比μ可以由室内或现场岩石力学试验确定，而由式(1)可知，切缝法向应力σθθ表达式中有3个独立的未知变量Sxx，Syy，Sxy，在进行原岩应力求解时，相互独立方程的个数不能<3个，即现场试验时需要布置至少3个不同夹角θ的切缝，并通过最小二乘法组合求解得到测试部位钻孔横截面的二维应力张量。

由于试验过程中并不能确定应力释放率ρ的数值，需要研究试验时达到的使应力完全释放的最小切缝深度。而且在同一测段需要布置3个以上切缝，每个切缝均应布置在其他切缝的影响带范围之外，因此需要结合有限元数值模拟研究优化切缝深度及切缝的影响范围，以优化测试时切缝的布置方案。

3 有限元计算模型的建立

在开展物理模型试验比较困难时，数值模拟是被广泛采用的一种研究手段。因此，本项目在进行切缝解除法地应力现场测试之前，采用有限元法对钻孔孔壁切缝解除过程进行数值模拟，主要研究切缝深度与应力释放率之间的关系、切缝过程中应力集中影响区域范围，优化试验过程及试验布置。

3.1 有限元模型

钻孔孔壁切缝解除是由空压机驱动的小型金刚石锯片(图3)，在钻孔孔壁上沿箭头方向逐级切出一条平行于钻孔轴线的切缝，进行数值模拟时，每级切割深度为2 mm。有限元模型尺寸为1 m×1 m×1 m，通过ABAQUS有限元分析软件进行数值模拟，采用C3D4单元，模型共划分为165 395个单元，29 390个节点。

图3 有限元模型及网格划分Fig.3 Finite element model and mesh division

3.2 岩体力学参数

参考锦屏地下实验室大理岩岩体力学试验结果，有限元模型中岩体力学参数取值如下：变形模量E0为45 GPa，泊松比μ为0.26。

4 切缝深度优化

4.1 计算工况及应力边界条件的选取

工程实践中，岩体初始应力场分布较复杂，最大主应力方位与切缝的夹角不同，切缝壁面应力完全释放所需的切缝深度不同。因此，本文选择了如表1所示的4个工况进行模拟研究。工况1，岩体应力以垂直于切缝的水平应力为主；工况2，岩体应力以平行于切缝的水平应力为主；工况3，岩体处于静水压力状态中，即各正应力相等；工况4，岩体应力以垂直于切缝的铅直向应力为主。鉴于锦屏地下实验室工程区位于锦屏山中部埋深最大部位，埋深一般>2 000 m，因此，模拟计算时计算模型取埋深2 000 m，铅直向应力取54.7 MPa。

表1 计算工况Table 1 Calculation conditions

4.2 切缝过程中应力演化过程分析

造孔完成后，各工况钻孔在不同部位出现了明显的应力集中区和应力降低区。图4给出了工况3造孔完成至切缝深度为30 mm时应力分量演化过程,本文仅给出造孔完成时及切缝深度为6，18，30 mm时的Szz分布等色图。

图4 工况3条件下Szz演化过程Fig.4 Evolution process of Szz in calculation condition 3

根据切缝两侧的应力分布图可知，钻孔后钻孔两侧出现明显的应力集中。随着切缝深度的增加，切缝部位岩体应力逐步降低，且应力集中区向切缝末端转移。由图4可知，当切缝深度到14 mm以后，切缝中部上下两侧应力分量Szz基本达到稳定。由图4(d)可知，当切缝深度为30 mm时，由钻孔形成的切缝处应力扰动区全部迁移至切缝底部，但由于切缝的扰动，切缝中部两侧岩体一定的范围内应力较钻孔周边未扰动区明显偏低。

图5 Szz应力分量随切缝深度的变化Fig.5 Change of Szz along narrow slot depth

图5给出了工况3切缝上部节点法向应力Szz由原岩应力、钻孔成孔后应力及切缝过程应力的变化过程。由图5可知钻孔成孔后，该切缝中部Szz应力分量有明显的应力集中:切缝深度为4 mm时，节点应力释放变为3.74 MPa;切缝深度为8 mm时为-1.1 MPa，节点应力由压应力转变为拉应力；当切缝深度达到14 mm以后，Szz基本稳定在-1.0 MPa。

4.3 切缝深度优化

模拟结果显示，各工况下切缝中间上部观测节点法向应变εz的演化规律相似，随着切缝深度的增加，切缝中间上部观测点法向应变εz逐步降低，当切缝深度达到一定深度后基本达到稳定。图6给出了工况2和工况4切缝中间上部观测点法向应变εz随切缝深度的变化情况。

图6 εz随切缝深度的变化Fig.6 Change of εz along narrow slot depth

由图6可知：工况2中，钻孔成孔后，切缝中部法向应变εz由0增大至-1.91×10-3，切缝深度为6 mm时为0.77×10-3，切缝深度为14 mm时为0.81×10-3，然后随切缝深度的增加，εz一直稳定在0.81×10-3。因此，εz的变化与切缝中部应力分量Szz相似，综合切缝过程中应力分量Szz的演化过程，可以认为该工况切缝深度到16 mm时，应力完全释放，即现场试验时切缝深度需达到16 mm以上。工况4中，切缝中部法向应变εz由0增大至-1.91×10-3，切缝深度为8 mm时为0.81×10-3，然后随切缝深度的增加，εz一直稳定在0.81×10-3。因此，综合切缝过程中应力分量Szz的演化过程，可以认为该工况切缝深度到10 mm时，应力完全释放，即现场试验时切缝深度需达到10 mm以上。

相对所模拟的4种工况，工况2切缝深度达到16 mm时切缝中间上部观测点方达到稳定，为4个工况中的最大值；工况4最小，为10 mm。即当初始应力场以平行于钻孔轴向应力分量为主时，所需的切缝深度较大。因此，为保证试验成果的可靠性，进行现场试验时切缝深度应至少达到16 mm，以使应力全部释放。

5 切缝布置间距优化

由4.3节模拟计算结果可知，工况2即当岩体应力以平行于切缝的水平应力为主时，切缝部位应力完全释放所需的切割深度最大，为16 mm。因此，本节以工况2为研究对象，研究切缝对孔周及孔径方向的影响，以优化切缝布置间距。

5.1 切缝对孔径方向的影响

在进行钻孔孔壁切缝应力解除试验时，切缝会在测试部位沿孔径方向形成一定范围的影响带(见图7)，为避免交叉影响，切缝必须布置在其他切缝的影响带之外。

图7 孔径方向影响带示意图Fig.7 Influenced band along the axis of borehole

在研究切缝的轴向影响时，在切缝的边缘处布置如图7所示的测线，根据测线上法向应变εz自切缝端点开始沿着轴向距离的变化情况确定切缝的影响范围。图8给出了工况2切缝深度为16，24，30 mm时的切缝轴线方向观测线上的应变εz的变化情况。

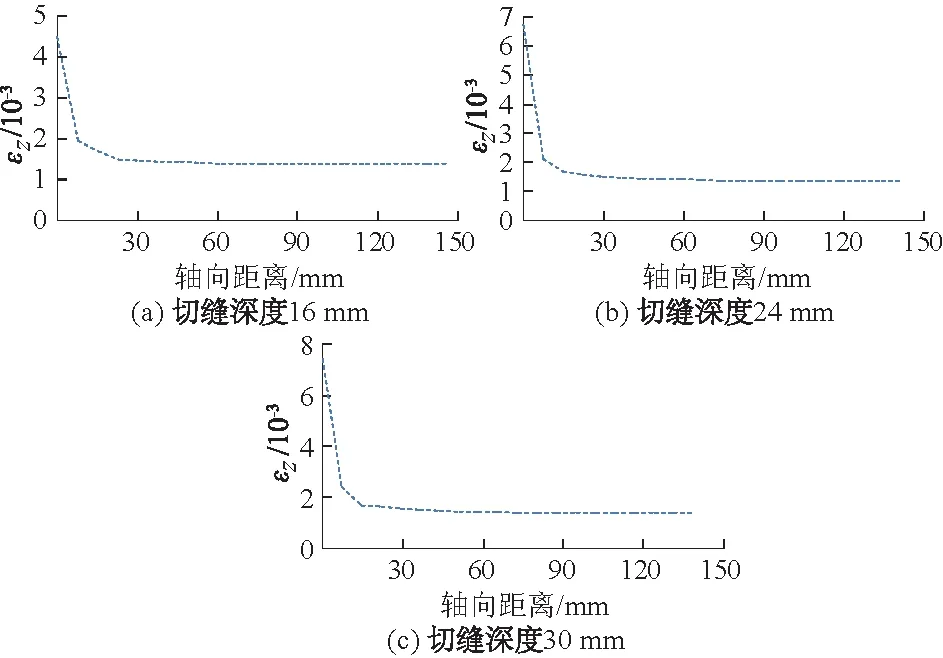
图8 不同切缝深度εz沿切缝轴向分布情况Fig.8 Distribution of εz along the axis of slot of different depths

由图8可知，切缝端点的应变εz为4.5×10-3，随着轴向距离的增加而减小，距轴向距离为约61 mm时趋于稳定至1.4×10-3。因此在进行现场试验时，在钻孔布置切缝应根据切缝深度选择合适的切缝间隔距离。当切缝深度为16 mm时，两切缝端部的间隔距离应≥122 mm。切缝深度为24 mm时，切缝的扰动范围约为74 mm，两切缝端部的间隔距离应≥148 mm。切缝深度为30 mm时，切缝的扰动范围约为91 mm，两切缝端部的间隔距离应≥182 mm。在进行现场试验时，在钻孔布置切缝应根据切缝深度选择合适的切缝间隔距离，一般情况下测缝布置间距应大于数值模拟得到的间距，因此，现场试验时，测缝间距的布置一般>200 mm。

5.2 切缝对孔周的影响

在进行现场试验时需要布置至少3个不同夹角θ的切缝，以求得钻孔横截面的二维应力张量，通常将3个不同切缝之间的夹角布置为120°。因此，需要研究切缝孔周的影响范围，以防止切缝之间互相影响而降低测试结果的可靠性。图9给出了工况2切缝前、切缝深度为16 mm时切缝法线方向应变εz的分布等色图。

图9 切缝前及切缝深度为16 mm时εz分布Fig.9 Distributionof εz before cutting and after cutting with 16 mm slot depth

对比图9(a)和图9(b)可知，当切缝深度为16 mm时，切缝孔周上下影响范围基本对称，上下影响带均约覆盖了53°的弧。在对应的应力状态下，切缝深度为16 mm时，切缝的分离角度应<106°，因此，在一个给定的钻孔深度可以布置3个切缝。但在实际操作中，为了提高试验的可靠性，避免切缝之间的相互影响，往往一个给定的钻孔深度只布置一个切缝。

6 工程应用

6.1 测试情况简介

锦屏地下实验室利用锦屏二级水电站引水隧洞的辅引1#,2#施工支洞，新开挖4组(共8条)130 m×14 m×14 m(长×宽×高)实验洞及相关辅助洞室。锦屏地下实验室工程区位于T2b白山组大理岩，处于高地应力环境中。高地应力的作用使得地下洞室的建设面临日益突出的高地应力问题，特别是施工期岩爆灾害的危险性大大增加。为了研究地下实验室的应力状态，在7#实验室掌子面布置了GS-8测孔,采用钻孔孔壁切缝应力解除法进行了地应力测量，钻孔布置见图10。

图10 钻孔布置示意图Fig.10 Arrangement of test boreholes

试验洞内测试钻孔均为灰白色厚层大理岩，岩性较脆，钻进取得的岩芯一般呈短柱状。钻进过程中，局部出现岩芯饼化现象(见图11)。根据模拟计算结果，同一钻孔深度只布置一个切缝，且切缝与切缝之间的距离为300 mm。

图11 岩芯照片Fig.11 Photos of drilling rock cores

6.2 测试结果分析

钻孔孔壁切缝法地应力测试结果整理的过程中需要岩体的弹性参数(E与μ)，结合现场取芯完整性及室内试验成果确定本次计算参数取岩石弹性模量为52.0 GPa，泊松比为0.22。表2为钻孔GS-8的测试结果，σA和σB分别为钻孔横截面最大及最小主应力，α为钻孔横截面最大主应力方位角，以铅直向上方向为0°，顺时针旋转方向为正。

在测试深度范围内，钻孔横截面最大主应力量值64.7～94.5 MPa，最小主应力为59.2～80.3 MPa，钻孔截面最大主应力方位角α为133°～155°，为陡倾角，说明测试部位岩体以铅直应力分量为主。

表2 GS-8钻孔测试结果Table 2 Measured results of borehole GS-8

测试结果给出了钻孔横截面上的主应力状态，应采用式(11)求测试钻孔横截面上的应力分量。

(11)

式中：σz为铅直向应力分量；σx为钻孔横截面水平方向应力分量；σzx为钻孔横截面剪应力。表3给出转换后的应力测试结果。

表3 转化后测试结果Table 3 Measured results after transformation

如果上覆岩体密度取为2.650 g/cm3，测试部位埋深约为2 300 m，则上覆岩体自重应力约为61.0 MPa。测试结果大于上覆岩体自重，主要因为GS-8钻孔位于7#实验室掌子面上，测试部位位于应力集中区，岩体应力较大，依据《水力发电工程地质勘察规范》(GB 50287—2006)，岩体应力>40 MPa，测试部位岩体处于极高应力环境中，因此在钻进过程中易出现如图11所示的岩芯饼化现象。

7 结 论

通过数值模拟研究了钻孔孔壁切缝解除法地应力测试时的优化布置方案，并将该方法用于锦屏地下实验室7#实验室的地应力测量中，主要结论如下：

(1)三维数值分析结果显示，为保证试验成果的可靠性，当初始应力场以平行于钻孔轴向应力分量为主时，切缝深度达16 mm时切缝两侧的应力全部释放；而当初始应力场以平行于切缝法线方向应力分量为主时,切缝深度为10 mm，应力即可全部释放。因此，为保证试验成果的可靠性，进行现场试验时切缝深度应至少达到16 mm。

(2)切缝深度为16 mm时，切缝孔周上下影响范围基本对称，上下影响带均约覆盖了53°的弧,切缝的分离角度应<106°，因此，在一个给定的钻孔深度可以布置3个切缝。但在实际操作中为了提高试验的可靠性,避免切缝之间的相互影响,往往一个给定的钻孔深度只布置一个切缝。

(3)当切缝深度增加时，切缝的轴向扰动范围随切缝深度的增加而增加。当切缝深度为16 mm时，两切缝端部的间隔距离应≥122 cm。

(4)锦屏地下实验室7#实验室GS-8钻孔位于应力集中区，铅直向应力分量大于根据上覆岩体自重估算应力。测试结果表明，测试部位岩体处于极高应力状态下，与钻孔钻进过程中出现岩芯饼化现象相符合。

[1] STEPHANSSON O, ZANG A. ISRM Suggested Methods for Rock Stress Estimation—Part 5: Establishing a Model for the in Situ Stress at a Given Site[J].Rock Mechanics and Rock Engineering, 2012, 45: 955-969.

[2] 刘允芳,朱杰兵,刘元坤.空心包体式钻孔三向应变计地应力测量的研究[J].岩石力学与工程学报,2001,20(4):448-453.

[3] HUDSON J A, F. H. CORNET F H, CHRISTIANSSON R. ISRM Suggested Methods for Rock Stress Estimation—Part 1: Strategy for Rock Stress Estimation[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(7):991-998.

[4] SJÖBERG J, CHRISTIANSSON R, HUDSON A. ISRM Suggested Methods for Rock Stress Estimation—Part 2：Overcoring Methods[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(7/8):999-1010.

[5] 蔡美峰,乔 兰,余 波,等.金川二矿区深部地应力测量及其分布规律研究[J].岩石力学与工程学报,1998,18(4):414-418.

[6] HAIMSON B. Hydraulic Fracturing in Porous and Nonporous Rock and Its Potential for Determining in-situ Stresses at Great Depth [R].Minneapolis: Minnesota University,1968.

[7] 葛修润，侯明勋.一种测定深部岩体地应力的新方法——钻孔局部壁面应力全解除法[J]．岩石力学与工程学报,2004,23(23):3923～3927.

[8] 艾 凯,尹健民,刘元坤,等.极高应力条件下岩体开挖面应力测量方法研究[J].岩石力学与工程学报,2012,31(增2):3974-3980.

[9] 刘允芳,艾 凯,尹健民,等.窄缝局部应力解除和窄缝弹性模量试验拓宽应用的研究[J].岩石力学与工程学报,2013,32(5):876-882.

[10] SAATI V，MORTAZAVI A. Numerical Modelling of in Situ Stress Calculation Using Borehole Slotter Test[J]. Tunnelling and Underground Space Technology, 2011, 26(1):172-178.