节理在初始接触状态下空腔分布的确定及应用

，, 2， ，，

(1.同济大学 地下建筑与工程系，上海 200092；2.绍兴文理学院 土木工程学院，浙江 绍兴 312000)

1 研究背景

节理岩体的力学和水力性质主要受其内部的节理影响，研究单个节理的力学和水力性质是研究节理岩体的基础。节理表面是粗糙不平的，节理面的粗糙特性对节理的剪切特性起到了主导作用[1-3]；上下节理面的粗糙程度及二者所组成的节理空腔更是影响节理渗流特性的主要因素，在节理剪切过程中，上下节理面在水平向发生剪切的同时在法向因为突起的存在而发生爬坡作用，2个方向的位移变化导致了节理空腔不断地发生变化[4-5]。由于现有技术水平的限制，难以获得节理剪切过程中的表面形貌数据及节理空腔数据。目前常用的解决方法是首先获得初始状态下节理表面形貌数据及节理空腔数据，在节理剪切过程中，将上下节理面数据根据剪切位移-法向位移进行错位，在这一过程中上下节理面相交的区域被认为是剪切破坏区域或者是发生弹性变形区域予以删除，最后获得节理剪切过程中的节理面形貌数据及节理空腔数据，进而为相应的研究提供模型基础[4,6]。故节理面初始形貌数据及接触状态是进行节理剪切和渗流特性研究的基础。

节理初始表面形貌数据的获得在技术方面已经比较成熟，目前常用的方法主要是使用三维激光扫描仪、光栅投影式形貌仪或者其他摄影测量设备来对单个节理面进行扫描[7-9]，进而获得节理面形貌数据。节理空腔的测量技术主要有：①利用低熔点的金属或者树脂填充节理空腔，对填充物厚度分布进行测量进而获得节理空腔数据[6,10-11],但是由于节理接触的存在，在试验过程中难以保证节理空腔被完全填充，而且此方法只能在试验前或试验后使用[12];②Re等[13]、Renshaw等[14]分别使用X射线和核磁共振的方法来测量节理空腔，但是这些方法只能定性地确定节理初始隙宽分布范围，难以作为后续计算分析的基础;③Koyama等[15]、Tang等[16]应用数值方法来计算节理初始空腔数据，即首先获得上下节理面数据，然后将上节理面置于下节理面之上，通过在竖向移动、旋转上节理面，使上下节理面有3个稳定接触点且上节理面重心位于3点所组成的三角形内则计算完毕，此时的节理接触状态便认为是节理的初始接触状态，进而可以得到节理的初始空腔。但是此种方法的弊端在于首先在接触状态计算之前难以确定上下节理面在平面方向的相对位置，其次3点接触的判断标准与上下节理的实际接触状态存在偏差。

为了解决初始节理空腔计算存在的上述问题，利用自行研制的TJXW-3D 型便携式岩石节理表面形貌测量仪分别对贴有标志点的上下节理面和上下节理面在初始接触状态下的整个试样进行扫描，扫描结束后利用标志点将上下节理面分别对齐到其在初始接触状态下的坐标系中，进而可以获得节理初始空腔数据。

2 试验概况

2.1 试样制备

通过劈裂花岗岩块来获得3组不同形貌的节理，节理平面尺寸为200 mm×100 mm；采用硅胶复制节理面的形貌，然后以此为模板浇筑石膏以制备节理试样，分别命名为J1，J2，J3。Barton[2]提出了节理粗糙度系数JRC来评价节理表面粗糙程度，并给出JRC为0～20的10条典型的节理剖面线。Tse和Cruden[17]提出了JRC与剖面线高度均方根Z2的关系式,即：

JRC=32.2+32.47lgZ2；

(1)

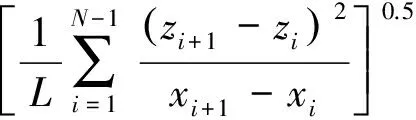
(2)

式中：xi，zi为剖面线坐标；L为剖面线长度；N为采样点数。计算得到的3组节理的JRC分别为：JRC1=11.5，JRC2=13.2，JRC3=15.3。

2.2 试验仪器

图1 形貌测量仪Fig.1 Apparatus of surface topography measurement

节理表面形貌的测量是本试验的主要内容，本试验采用的是基于3D光栅投影测量原理的TJXW-3D型便携式岩石节理表面形貌测量仪，该测量系统具有精度高、单面扫描速度快、易于操作、可实现多个单幅测量数据的自动拼接等特点。系统主要包括机头、三脚架、计算机和标定板，见图1。机头利用螺栓固定在三脚架顶部，方便拆卸，机头主要由光栅投影装置和2个CCD摄像机组成。测量时机头朝下向被测物体投射测量光栅，机头与被测物体距离在50 cm左右为最佳。系统单次测量精度为0.02 mm，其他具体参数参见文献[18]。

压缩试验使用岩石节理全剪切-渗流耦合试验系统，该试验设备由主机加载框架、液压系统、伺服控制系统、计算机控制及处理系统4大部分组成。该设备能够实现PC控制全自动加载，同步记录各项变形、位移、荷载数据。法向位移采用位移传感器测量，位移传感器测试精度为0.001 mm。

2.3 试验方法

对于一个节理试样，首先能够分别获得上下节理面的形貌数据和上下节理面处于初始闭合状态下的相对位置。如果能够将上下节理面的数据分别对齐到上下节理面处于初始闭合的状态，便可以获得节理在初始闭合状态下的空腔数据。TJXW-3D型便携式岩石节理表面形貌测量仪自带的测量软件可以识别特定的标志点为特征点，并对具有共同特征点的数据按照特征点之间的距离不变原则进行拼接。首先要对侧面贴有标志点的处于初始闭合状态的节理试样进行扫描，在此之后，分别对上下节理面进行扫描，侧面的标志点同时也被扫描记录，软件会自动根据贴在试样侧面的标志点将上下节理面分别对齐到初始偶合接触状态下的扫描数据。这样，初始偶合状态下节理空腔可以根据式(3)计算得到。

zaperture(xi,yi)=zupper(xi,yi)-zlower(xi,yi)。

(3)

式中：zaperture(xi,yi)为节理空腔数据;zupper(xi,yi)，zlower(xi,yi)分别为上、下节理面形貌数据。

在获得节理形貌数据的过程中，每个节理面要在不同方位进行多次扫描才可以拼接得到一个完整的节理面数据，因为只有同时出现在2个CCD镜头中的对象才会被扫描成功。

节理闭合试验在岩石节理全剪切-渗流耦合试验系统上进行，采用4支位移传感器采集节理法向闭合变形，并以其平均值来表征节理法向闭合变形。法向荷载为80 kN(4 MPa)，加载速率为1 kN/s。

3 初始接触状态下节理空腔分布

利用本文第2节介绍的方法分别对试样J1，J2，J3的上下节理面的形貌数据和节理空腔结果进行了计算，计算过程见图2，计算结果见图3。

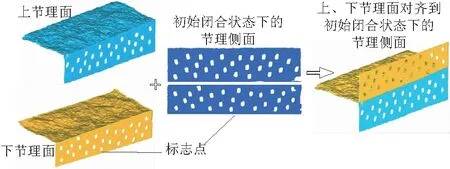
图2 节理空腔计算过程Fig.2 Computation of void space of joint

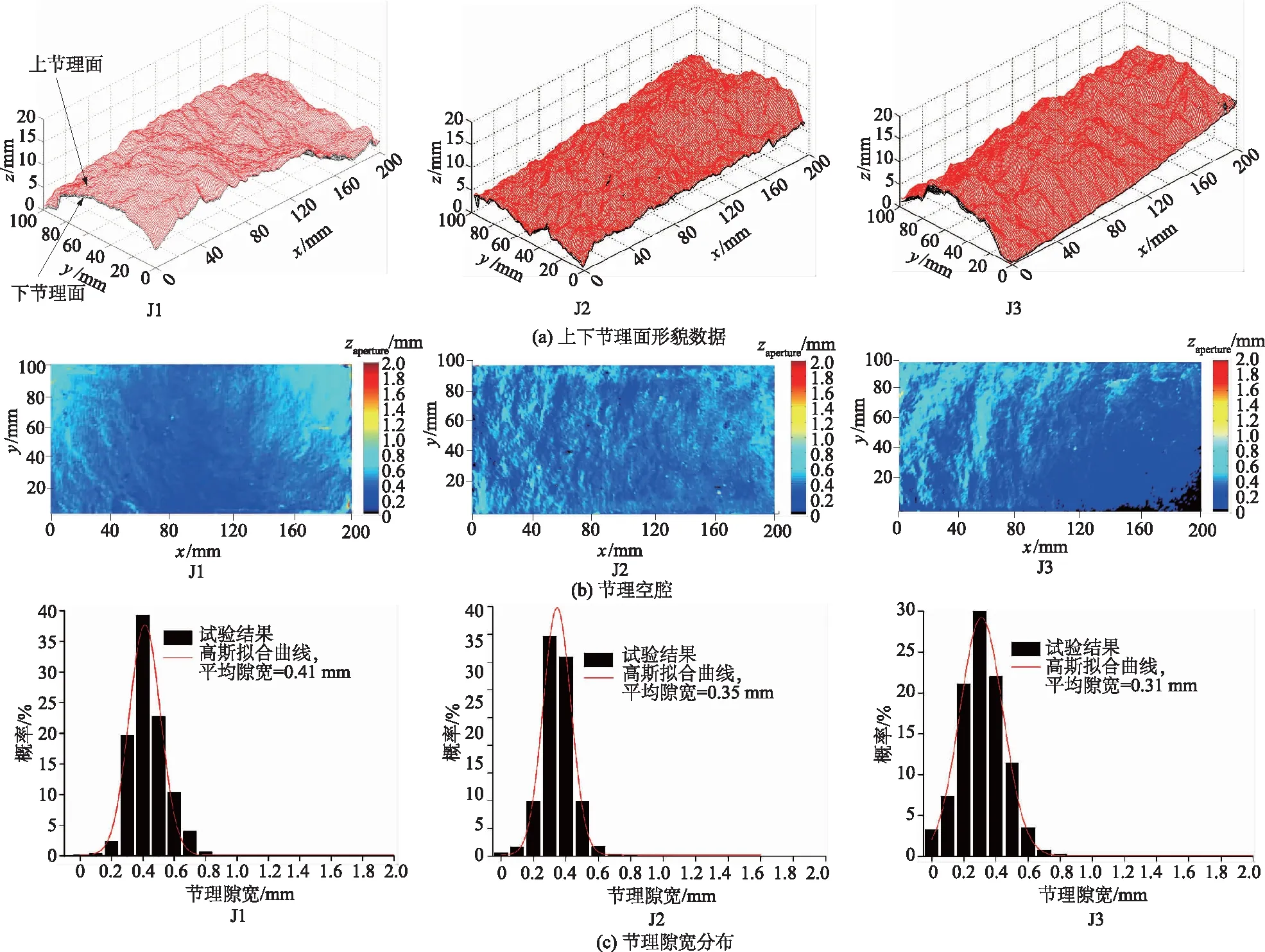
图3 节理空腔计算结果Fig.3 Computation result of joint’s void space

图3(a)给出的各节理上下表面形貌数据可以看到，节理J1表面具有较大的一阶起伏度，J2表面则明显以二阶粗糙度为主，J3节理表面一阶起伏度和二阶粗糙度都可以清楚地分辨出来。

图3(b)给出了黑色区域代表节理接触区域。J1上下节理接触区域较小，J2上下节理面接触区域零星分布于整个节理空腔，J3的节理接触则主要分布于边缘位置，且接触面积为J3>J2>J1。

从图3(c)给出的各节理隙宽概率分布也可以得到同样的结论，J3节理的初始接触面积最大，在3.3%左右。根据计算得到的节理空腔结果，统计了不同隙宽的概率分布，可见各组节理空腔分布遵循高斯分布。从图3(c)中也可以看出节理初始平均隙宽J1(0.41 mm)>J2(0.35 mm)>J3(0.31 mm)，这与Hakami等[12]的研究结果基本吻合。Hakami等[12]使用树脂材料填充节理空腔得到了耦合花岗岩的在低法向应力(0.45 MPa)作用下的空腔分布，结果表明节理隙宽分布同样均遵循高斯分布，且统计的初始接触面积均在5%以下，平均隙宽为0.36 mm。

4 节理空腔数据的应用

Greenwood等[19]将粗糙表面的微凸体视为球形，基于Hertz理论和概率统计理论提出了光滑平面与粗糙平面接触的变形模型，以下简称Greenwood模型。Brown和Scholz[20]在Greenwood模型的基础上，利用节理的组合形貌提出了节理闭合模型——Brown模型，即：

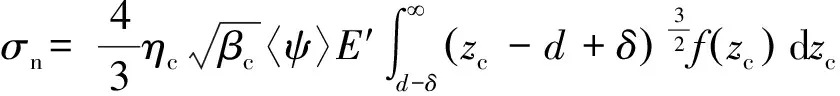
(4)

(5)

式中：σn为法向应力;ηc为节理组合形貌的峰点密度；βc为节理组合形貌的峰点平均半径；〈ψ〉为切向应力相关因子的平均值，通常〈ψ〉≈1；E′为有效弹性模量；E，ν分别为弹性模量和泊松比；zc为随机变量，表示组合形貌某峰顶到参考面的距离；d为上下节理面参考面之间的距离;δ为节理法向闭合变形。

计算节理的组合形貌是Brown模型的基础，图4给出了节理空腔与节理组合形貌之间的关系。在这里，利用本文的节理空腔数据来计算得到节理的组合形貌，进而可以方便地应用Brown模型，并与实际的压缩试验结果进行对比。

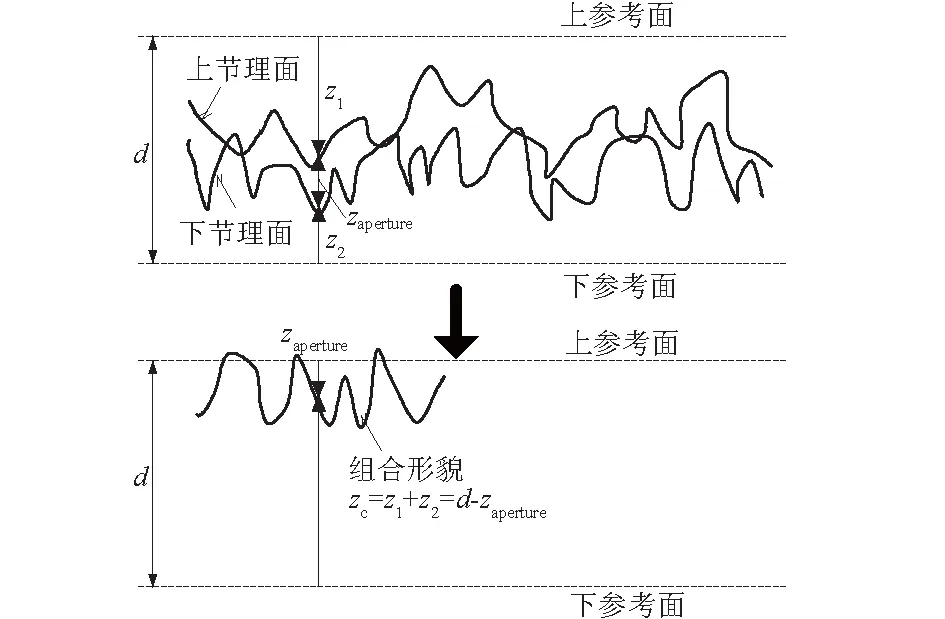
图4 节理组合形貌与节理空腔的关系Fig.4 Relationship between composite topography and void space

由图5可见，在同一法向应力下，Brown模型预测结果总是比法向位移实际试验结果大。经分析，主要原因在于:虽然Brown模型是在Greenwood模型上进行改进的，但其基本假设相同，即认为突起具有完全相同的突起半径且互不影响;在实际情况下，突起在被压缩的过程中会牵动突起周边的节理面,受力面积不仅限于各突起(实际受力的不只是Greenwood所假设的突起)，而且各突起互相之间具有约束作用。所以Brown模型预测的节理变形会比试验结果要大。

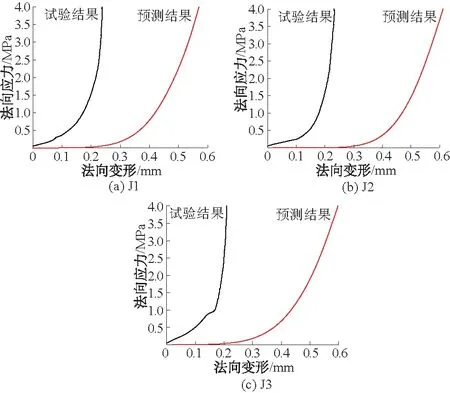
图5 Brown模型预测结果与试验结果的比较Fig.5 Comprison between Brown model’s result and test result

5 结 论

本文介绍了确定节理在初始接触状态下空腔分布的新方法，初步探索了3个不同粗糙度节理试样的初始隙宽分布规律以及节理初始空腔数据在Brown法向闭合模型中的应用。所介绍的方法在节理剪切-渗流的研究中，尤其是为节理剪切渗流的数值研究奠定了模型基础。

(1)利用自行研制的TJXW-3D型便携式岩石节理表面形貌测量仪分别对上下节理面和上下节理面在初始接触状态下的整个试样进行扫描，扫描结束后利用标志点将上下节理面分别对齐到其在初始接触状态下的坐标系中，进而可以获得节理初始空腔数据。

(2)利用本文介绍的节理初始空腔计算方法对3个不同粗糙度的节理进行计算，得到了各节理初始空腔数据，并统计了各节理隙宽的分布规律。各节理隙宽分布符合高斯分布，平均隙宽为0.31～0.41 mm，与Hakami等的研究所得结论基本一致。

(3)将本文计算得到的节理初始空腔数据应用到节理法向闭合Brown模型中，Brown模型预测结果比实际试验结果相对较大，经分析主要原因在于Brown模型无法考虑各突起之间的相互作用。

[1] PATTON F D. Multiple Modes of Shear Failure in Rock[C]∥International Society for Rock Mechanics and Rock Engineering，1st ISRM Congress，Lisbon，Portugal，September 25-October 1，1966：509-513.

[2] BARTON N. Review of a New Shear-strength Criterion for Rock Joints[J]. Engineering Geology，1973，7(4)：287-332.

[3] 唐志成，夏才初，宋英龙，等.Grasselli节理峰值抗剪强度公式再探[J]. 岩石力学与工程学报，2012，31(2) ：356-364.

[4] XIA C C，GUI Y，WANG W，etal. Numerical Method for Estimating Void Spaces of Rock Joints and the Evolution of Void Spaces under Different Contact States[J]. Journal of Geophysics and Engineering，2014，11(6):065004.doi:10.1088/1742-2132/11/6/065004.

[5] GUI Y，XIA C C，DING W Q，etal. A New Method for 3D Modeling of Joint Surface Degradation and Void Space Evolution under Normal and Shear Loads[J]. Rock Mechanics and Rock Engineering, 2017，50(10):2827-2836.

[6] PARK J W, SONG J J. Numerical Method for the Determination of Contact Areas of a Rock Joint under Normal and Shear Loads[J]. International Journal of Rock Mechanics and Mining Sciences，2013，58:8-22

[7]GRASSELLI G, WIRTH J, EGGER P. Quantitative Three-dimensional Description of a Rough Surface and Parameter Evolution with Shearing[J]. International Journal of Rock Mechanics and Mining Sciences，2002，39(6):789-800.

[8]BELEM T，SOULEY M，HOMAND E F. Method for Quantication of Wear of Sheared Joint Walls Based on Surface Morphology[J]. Rock Mechanics and Rock Engineering，2009，42(6):883-910.

[9] FATHI A，MORADIAN Z，RIVARD P，etal. Geometric Effect of Asperities on Shear Mechanism of Rock Joints[J]. Rock mechanics and Rock Engineering，2016，49(3):801-820.

[10] GENTIER S, BILLAUX D,VAN VLIET L. Laboratory Testing of the Voids of a Fracture[J]. Rock Mechanics and Rock Engineering，1989，22(2):149-157.

[11] NEMOTO K，WATANABE N，HIRANO N，etal. Direct Measurement of Contact Area and Stress Dependence of Anisotropic Flow Through Rock Fracture with Heterogeneous Aperture Distribution[J]. Earth and Planetary Science Letters，2009，281(1/2):81-87.

[12] HAKAMI E,LARSSON E.Aperture Measurements and Flow Experiments on a Single Natural Fracture[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1996，33(4):395-404.

[13] RE F, SCAVIA C. Determination of Contact Areas in Rock Joints by X-ray Computer Tomography[J]. International Journal of Rock Mechanics and Mining Sciences，1999，36(7):883-890.

[14] RENSHAW C E，DADAKIS J S，BROWN S R. Measuring Fracture Apertures: A Comparison of Methods[J]. Geophysical Research Letters，2000，27(2):289-292.

[15] KOYAMA T，FARDIN N，JING L，etal. Numerical Simulation of Shear-induced Flow Anisotropy and Scale-dependent Aperture and Transmissivity Evolution of Rock Fracture Replicas[J]. International Journal of Rock Mechanics and Mining Sciences，2006，43(1):89-106.

[16] TANG Z C, LIU Q S, XIA C C，etal. Mechanical Model for Predicting Closure Behavior of Rock Joints Under Normal Stress[J]. Rock Mechanics and Rock Engineering，2014，47(6):2287-2298.

[17] TSE R, CRUDEN D M. Estimating Joint Roughness Coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1979，16(5):303-307.

[18] 夏才初，王 伟，丁增志.TJXW-3D型便携式岩石三维表面形貌仪的研制[J].岩石力学与工程学报，2008，27(7)：1505-1512.

[19]GREENWOOD J A，TRIPP J H. The Contact of Two Nominally Flat Rough Surfaces[J]. Proceedings of the Institution of Mechanical Engineers，1970，185：625-633.

[20] BROWN S R，SCHOLZ C H. Closure of Random Elastic Surfaces in Contact[J]. Journal of Geophysical Research，1985，90(B7)：5531-5545.