考虑电网阻抗的风电变流器稳定控制方法

宁尚贤, 辛绍杰, 杨恩星, 陈慧婷

(1.上海电气输配电集团 技术中心， 上海 200233；2.上海电机学院 电气学院， 上海 201306；3．远景能源(上海)有限公司， 上海 200051)

在分布式可再生能源向电网传输电能的电力网络中，由于输电距离跨度较大，使得电力网络中的电网阻抗成为不可忽略的因素[1-3]，导致并网逆变器与电网之间的联系较弱，形成一种弱电网状态[4-5]。此时，并网逆变器与电网之间形成了交互系统，使得并网逆变系统输出的并网电能质量会受到电网阻抗变化的扰动，不利于整个系统的稳定性[6-11]。因此，研究考虑电网阻抗的风电变流器稳定控制方法对并网环节具有重要意义。

本文分析了电网阻抗变化对连续域和离散域的并网逆变控制系统的影响，研究了电网阻抗自适应的控制方法，在Matlab/Simulink环境中搭建电网阻抗自适应的并网逆变器控制系统的仿真模型，进行了仿真验证。结果表明，该方法对维持并网逆变控制系统的稳定具有一定作用。

1 电网阻抗对三相并网逆变系统的影响

由于并网公共点与电网间的阻抗不能忽略，故并网逆变器与电网之间形成交互系统。图1所示为考虑电网阻抗的并网逆变器控制系统模型。

图1 考虑电网阻抗时并网逆变器控制系统模型

图中，在并网公共点PCC处引出并网侧电流反馈，UDC为并网逆变器直流侧电压;Ug为电网电压;Gc(s)为电流控制器，为抑制LCL滤波器产生的谐振，引入电容电流有源阻尼因子kd；在考虑三相并网逆变器中开关桥臂过流保护的情况下，电容电流由逆变侧电流与并网侧电流相减所得[12-13]；i1为并网逆变器侧输出电流;iC为经过LCL滤波电容Cf的电流;UC为电容电压;i2为并网侧电流;Zg为与输电网络等效的电网阻抗;i2αref，i2βref为参考电流。

(1)

由式(1)可见，电网阻抗Zg的加入改变了理想情况下并网逆变器电流环控制系统的传递函数，使控制系统的稳定受到影响；同时，当忽略Zg中的电阻Rg时，只相当于改变了并网侧的电感量L2。

图2 考虑电网阻抗的并网逆变控制系统电流环控制框图

为进一步分析电网阻抗对并网控制系统的影响，图3给出了Rg和Lg变化时的开环传递函数伯德图。由图3(a)可见，忽略Zg中的电抗后，当Rg=0 Ω时，控制系统的幅值裕度GM=13.7 dB，相角裕度PM=55.9°；当Rg=1 Ω时，GM=16.5 dB，PM=63.7°；当Rg=2 Ω时，GM=18.9 dB，PM=69.4°。可见，随着Zg中Rg的增加，控制系统的GM和PM也随之增加，表明并网逆变器控制系统的稳定性有一定增强。由图3(b)可见，忽略Zg中的电阻后，当Lg=1 mH时，GM=15.1 dB，PM=33.4°；当Lg=2 mH时，GM=16.4 dB，PM=27.5°。可见，随着Zg中Lg的增加PM降低，对控制系统的稳定性产生影响。

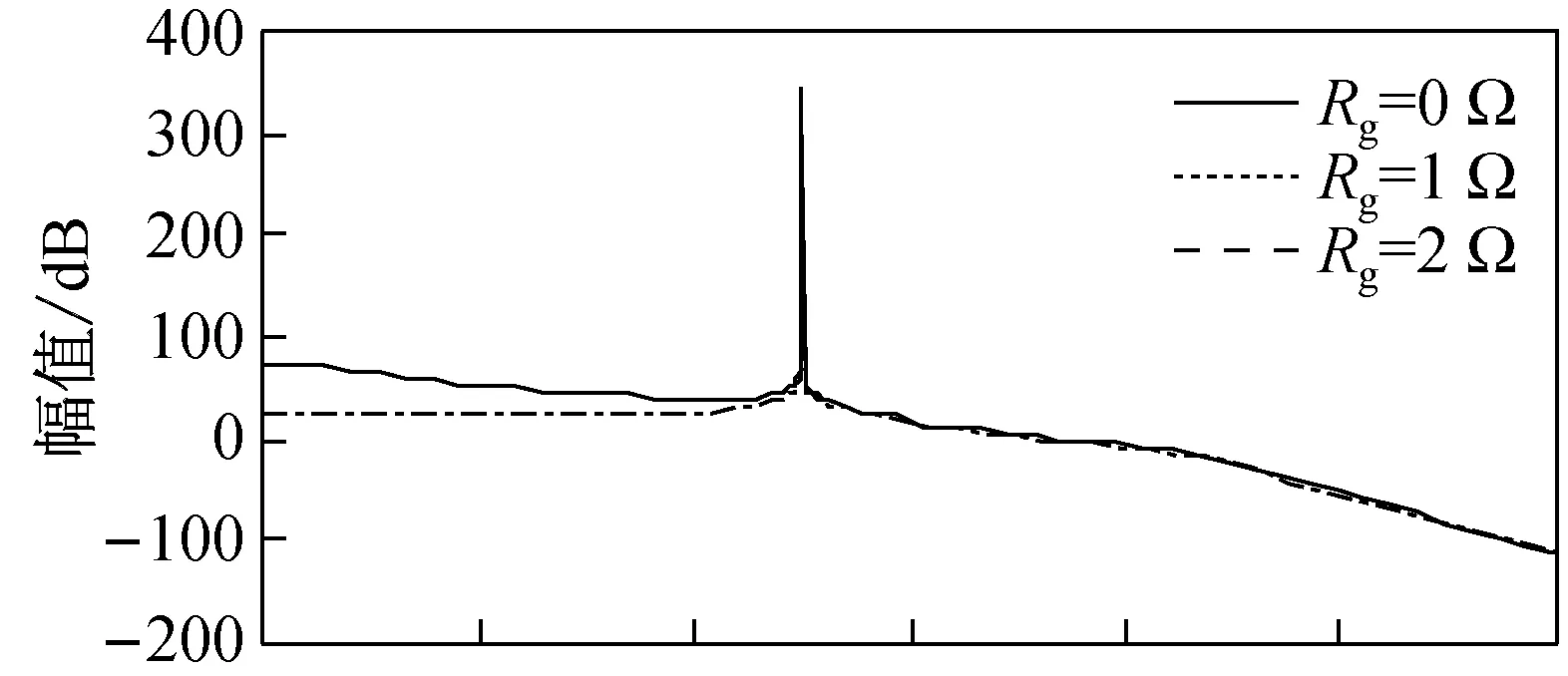
(a) Rg变化时

(b) Lg变化时

图3Rg和Lg变化时的开环传递函数伯德图

此外，由于并网逆变器控制系统中采用的是电容电流有源阻尼控制，故还需考虑当Zg变化时，阻尼比ζ所受到的影响，即

(2)

由式(2)可得到ζ与Zg的变化情况，如图4所示。由图4(a)可见，当Zg中Rg不变时，ζ随着Lg的增加而增加；由图4(b)可见，当Zg中Lg不变时，ζ随着Rg的增加而减小。由此可见，Rg的存在在一定程度上抑制了ζ的增加，因此，Zg的存在不会影响电容电流有源阻尼的稳定。

(a) Rg变化时

(b) Lg变化时

2 并网逆变控制系统在离散域的稳定性分析

为进一步分析在考虑电网阻抗时复杂控制系统的稳定性，对在连续域的并网逆变器电流环传递函数进行离散化处理[14-15]，可得在离散域下并网逆变器电流环控制框图，如图5所示。

图5 离散域并网逆变器电流环路的控制框图

为使在连续域的电流环开环传递函数离散化，本文采用双线性变换方法，可得离散域并网电流控制环路的传递函数为

(3)

式中：T为离散系统的采样频率；z为离散变化的变量。

故由式(3)和(1)可得离散域电流环传递函数为

(4)

式(4)所示的离散域电流环传递函数中没有考虑Zg，即Rg=0，Lg=0时的离散域系统模型。由离散域的传递函数，可依据奈奎斯特判据进行稳定分析[16]，图6所示为不考虑Zg时离散系统的奈奎斯特图。

(a) 离散域下

(b) (-1,j0)点处

由图6(a)可见，在离散域下，由于所示范围较大，图中观察不到(-1,j0)点，不能确定奈奎斯特曲线与负实轴的交点是否位于(-1,j0)点的右侧；故图6(b)给出(-1,j0)点处的奈奎斯特图。由图可见，不考虑Zg时离散系统的奈奎斯特曲线不包围(-1,j0)点，表明离散系统是稳定的。

而考虑Zg时，需在并网电流控制环路的传递函数中加入Rg,Lg分量，得到离散域电流环传递函数为

(5)

故得到考虑电网阻抗时离散系统的奈奎斯特图如7所示。由图可见，加入Zg后，离散系统的奈奎斯特曲线与负实轴的交点位于(-1,j0)的左侧，且逆时针包围了(-1,j0)点，故在考虑Zg后，离散系统的稳定性受到影响。

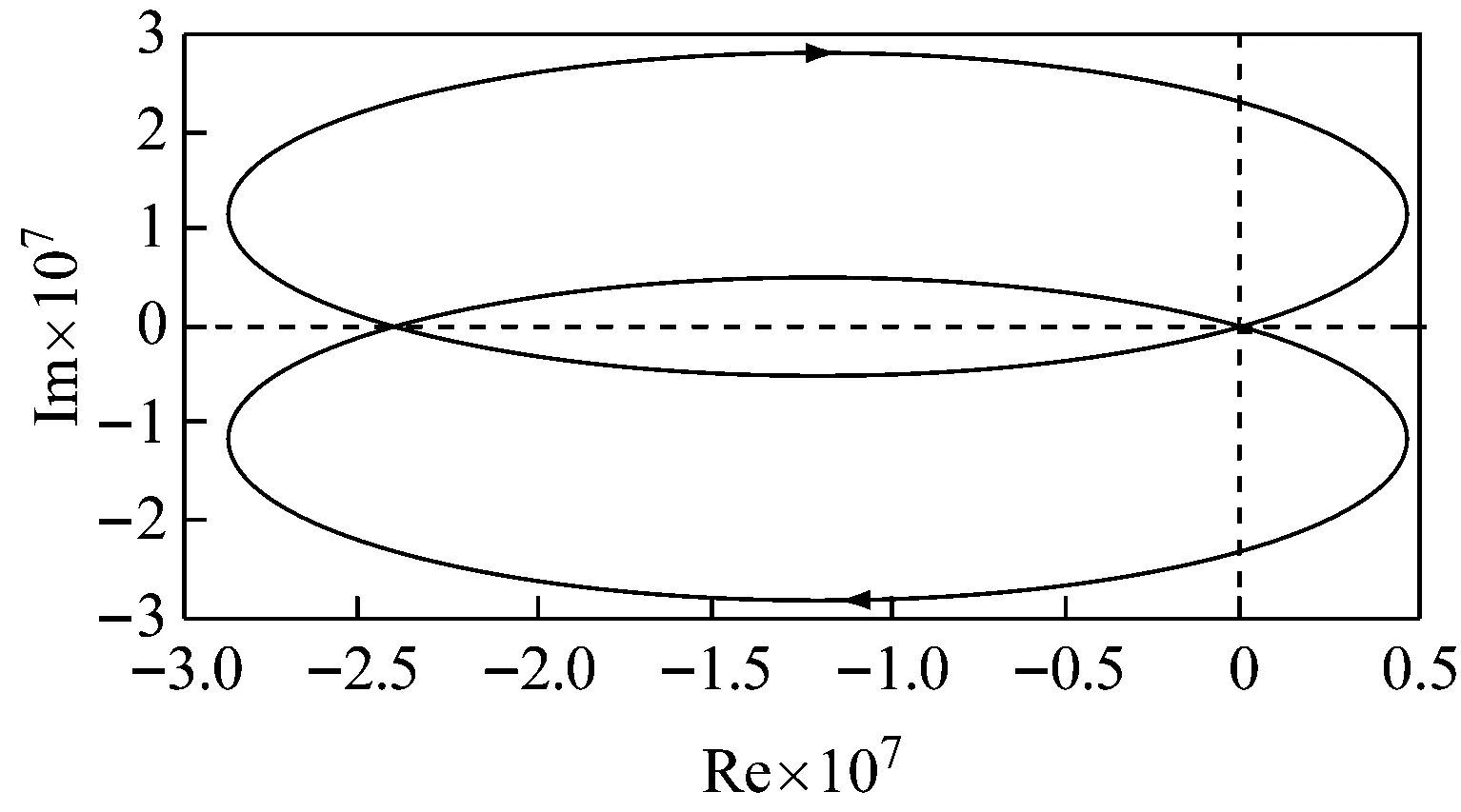
图7 考虑电网阻抗时离散系统的奈奎斯特图

3 电网阻抗自适应的控制方法设计

上述分析可知，Zg的存在使得并网逆变控制系统的稳定性受到影响。在不改变三相带LCL滤波的并网逆变系统结构的情况下，要使系统恢复稳定，只有通过调整并网逆变控制系统中电流控制环节的控制器参数比例系数kP、谐振系数kr以及kd，才能使系统的输出电压、电流得到改善。

并网逆变控制系统

(6)

(7)

(8)

式中：fc为并网逆变系统截止频率；f0为基波频率；ω0为基波角频率；Tf0为并网逆变系统低频增益。

由式(6)～(8)，本文建立了自适应Zg变化的并网逆变系统结构，如图8所示。图中,ith为非特征谐波电流。该控制系统主要包括4个部分：Zg检测部分；根据Zg调节控制参数部分；电流环控制环节；电容电流的前馈控制环节。

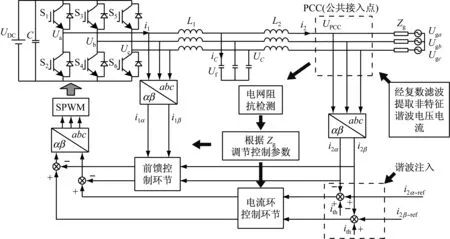
图8 自适应电网阻抗变化的三相并网逆变控制系统结构

自适应Zg变化的控制流程如图9所示。

图9 自适应电网阻抗变化的并网逆变控制系统流程图

其基本步骤如下：

(1) 在并网逆变器稳定运行后，进入Zg检测环节，在电流基准处注入非特征谐波电流，在并网公共耦合点处，提取为并网电压和并网电流注入非特征谐波频率下的分量；

4 仿真验证

基于自适应电网阻抗变化的控制方法的基本思路，在Matlab/Simulink中根据图8搭建了自适应电网阻抗变化的并网逆变控制系统仿真模型，进行仿真实验。

设置仿真系统参数如下：UDC=1.2 kV，Ug=690 V，f0=50 Hz，ω0=314 rad/s，Tf0=60 dB，fc=1 kHz，KPWM=600，ζ=0.7，仿真时间t=0.6 s。仿真开始时，并网逆变系统中Rg=7 Ω，Lg=25 mH；当t=0.3 s时，调整Zg，此时，Rg=5 Ω，Lg=20 mH。仿真中，设置Zg改变发生模块的短路开关，先保持其开路状态，当t=0.3 s时开关闭合，则电网中Rg=5 Ω，Lg=5 mH。

为验证本文研究的自适应Zg变化的并网逆变控制系统稳定性的作用，图10分别给出了三相带LCL滤波的并网逆变系统在并网公共耦合点处自适应Zg变化前、后的电压与电流的仿真波形。

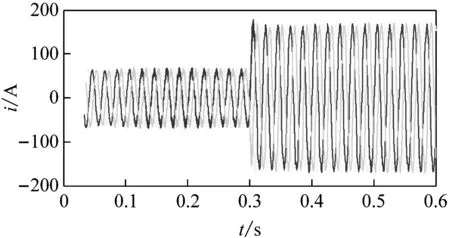
(a) 自适应变化前并网电流

(b) 自适应变化后并网电流

图10自适应Zg变化前、后的并网电压与并网电流的仿真波形

由图10(a)、(c)可见，在自适应Zg变化前，系统中Zg发生变化前、后输出的并网电压和并网电流波形均有波动产生，表明此时控制参数与电网阻抗不满足对应关系，故并网逆变控制系统稳定性受到影响；由图(b)、(d)可见，自适应Zg变化后，系统在Zg发生变化前、后输出的并网电压和并网电流波形均较为稳定，表明控制参数能够自适应Zg变化进行调整。

图11所示为自适应Zg变化前、后的并网电压与并网电流的傅里叶分析结果。

(a) 自适应变化前的并网电流

(b) 自适应变化后的并网电流

(d) 自适应变化后的并网电压

由图可见，采用自适应控制后，并网电流和并网电压的谐波含量有较大改善，且它们的基波幅值分别提高了0.2和1.8，总谐波失真率THD分别降低了2.03%和184.62%，表明采用自适应控制后，控制参数随Zg的变化而改变，改善了并网电流和并网电压中的谐波分布，其中，对并网电压的改善更为明显，使得并网逆变控制系统输出的并网电压和电网电流中的基波含量提高，减少了谐波的干扰。仿真表明，本文设计的Zg自适应控制方法对维持并网逆变控制系统的稳定具有一定的作用。

5 结 语

在考虑电网阻抗影响的情况下对风电变流器稳定控制方法进行研究，分析了电网阻抗的变化对连续域和离散域的并网逆变控制系统的影响，对复杂控制系统的稳定性做了进一步分析，从而研究了电网阻抗自适应的控制方法，建立了自适应电网阻抗变化的三相并网逆变控制系统，并在Matlab/Simulink环境中搭建仿真模型，对电网阻抗发生变化的情况进行了仿真验证。仿真结果表明，该方法对维持并网逆变控制系统的稳定具有一定的作用。

[1] 张馨月. 弱电网条件下并网变流器控制策略的研究 [D].北京交通大学,2015:1-30.

[2] 谢少军,季林,许津铭. 并网逆变器电网阻抗检测技术综述 [J].电网技术,2015,39(2):320-326.

[3] 唐婷,谢少军,焦鑫艳. 基于电网阻抗测量的新型主动式孤岛检测法 [J].电源学报,2012(6):60-64.

[4] 华淼杰. 弱电网条件下并网逆变器控制系统的稳定性分析 [D].南京：南京航空航天大学,2014:8-31.

[5] 汤婷婷,张兴,谢东，等. 基于高频注入阻抗检测的孤岛检测研究 [J].电力电子技术,2013,47(3):70-72.

[6] 陈新,张旸,王赟程. 基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响 [J].中国电机工程学报,2014,34(27):4559-4567.

[7] KRISHNA H. Computational aspects of the bilinear transformation based algorithm for S-plane to Z-plane mapping [J]. IEEE Transactions on Automa-tic Control, 1988, 33(11): 1086-1088.

[8] GROUTAGE F, VOLFSON L, SCHNEIDER A. S-plane to Z-plane mapping using a simultaneous equation algorithm based on the bilinear transformation [J]. IEEE Transactions on Automatic Control, 1987, 32(7): 635-637.

[9] CESPEDES M, SUN Jian. Adaptive control of grid-connected inverters based on online grid impedance measurements [J].IEEE Transactions on Sustainable Energy, 2014,5(2):516-523.

[10] ARIF B, TARISCIOTTI L, ZANCHETTA P, et al. Grid parameter estimation using model predictive direct power control [J]. IEEE Transactions on Industry Applications, 2015, 51(6): 4614-4622.

[11] 王要强. LCL滤波的并网逆变系统及其适应复杂电网环境的控制策略 [D].哈尔滨：哈尔滨工业大学,2013:1-16.

[12] VESTI S, SUNTIO T, OLIVER J A, et al. Impedance-based stability and transient-performance assessment applying maximum peak criteria [J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2099-2104.

[13] 周林,张密. 大型光伏电站谐振现象分析 [J]. 电力自动化设备,2014,34(6):8-14.

[14] 杨明,周林,张东霞，等. 考虑电网阻抗影响的大型光伏电站并网稳定性分析 [J]. 电工技术学报,2013,28(9):214-223.

[15] 杨明. 大型光伏电站逆变器并网控制策略及稳定性分析 [D].重庆：重庆大学,2014:45-72.

[16] 胡寿松. 自动控制原理[M].北京:科学出版社, 2007.