基于Adam s的一种新型平台的运动仿真

崔　智，李年裕，杨怀彬，余建莹

（1.陆军装甲兵学院，北京　100072； 2.大连理工大学盘锦校区，辽宁　盘锦　124000）

引言

履带式移动平台的一项重要性指标是机动性能，所谓机动性能就是在特定的环境和条件下平台能够快速顺利完成指定的运动路径的能力[2]。主要包括平台行驶的快速性、灵活性、通过性和长时间行驶的能力[3]。然而传统履带式平台在运动过程中存在着转向困难、运动中对履带板磨损严重等一系列问题，因此需要研制一种新型履带式行走装置从根本上解决上述问题。

对于军用履带式行走装置来说，各种技战术动作都是需要在行走装置灵活的转向性能上实现，因此研制转向性能强的新型履带式行走装置更有利于提升军用履带式行走装置的生存能力和防护性能，同时对于军事应用的发展也有重大的意义。

1　平台结构

1.1　平台履带结构

该平台履带结构与传统履带结构相类似，主要由主动轮、负重轮、诱导轮、托带轮、履带板、辊轮等部件组成，履带结构如图1所示，其主要特征在履带板上增加了具有一定偏角的辊轮支架，每个支架上纵向对称放置2组共4个小辊轮，履带板结构如图2所示，辊轮轴线与主动轮轴线构成一定夹角，定义为辊轮偏置角。每个履带板上放置4个小辊轮增加了履带板的接地面积，增强平台的稳定性能。履带板设计成中空的矩形板，主要是为了减轻履带板的重量。

图1　履带结构

图2　履带板结构

1.2　平台布局结构

平台的整体结构与传统的履带平台布局相类似，采用平台两侧各一条履带放置，如图3所示，中间矩形框为平台主体，两侧矩形框代表平台两侧履带，两侧矩形框中的小斜线代表辊轮轴线方向。

图3　平台的整体结构

2　平台运动学分析

履带平台在直线行驶时，履带跟随平台相对于地面的运动称之为牵连运动，相对于平台的运动称之为相对运动，二者复合而成的运动称之为绝对运动[4]。履带平台在转向行驶时，牵连运动是履带跟随平台相对于地面的旋转运动。定义平台牵连速度为vq；相对运动速度为vx；绝对运动速度为vj；三者间关系为：

该平台履带有两个自由度，分别为沿履带卷绕方向和辊轮滚动方向。这两个方向上速度矢量和为该履带的相对运动速度vx，对该平台履带上任意一接地点速度进行分析，如下页图4所示。

图4　平台履带上任意一接地点速度分析

图4中xoy是以主动轮中心o为原点的直角坐标系，r是主动轮半径，ω是主动轮角速度，va是履带板卷绕速度，o'、o"分别为偏置角为±γ的辊轮上的接地点，将每个履带板上一侧的两个辊轮看作一个整体，x'o'y'、x"o"y" 分别是以 o'、o" 为原点的直角坐标系，并满足ox//o'x'//o"x"。将o'和o"点上的相对速度分解到垂直于辊轮轴线方向上和履带的卷绕方向上分别得到 Veo'、Vao'和 Veo"、Vao"。

假设履带是不可拉伸且柔软的，因此：

接地点o'和o"相对运动速度为：

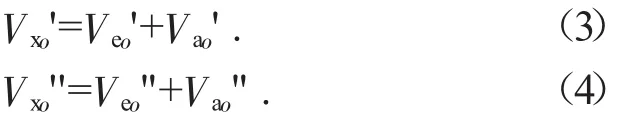
假设履带滑移滑转不被考虑的情况下，履带接地点绝对速度为0，即牵连速度与相对运动速度大小相等、方向相反。带式（1）中，得：

定义 o'、o" 接地点牵连速度分别为 vq'、vq''，将其分别分解到 x'、y'和 x''、y''轴上得到 Vqx'、Vqy'和 Vqx''、Vqy''。

联立式（2）（3）（5）得：

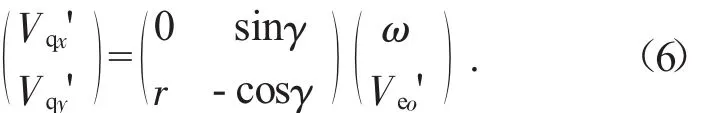
联立式（2）（4）（5）得：

通过式（6）（7）发现，该平台履带根据辊轮偏置角不同等效分为两部分，每一部分均拥有横向、纵向两个方向的牵连运动速度分量。

当整个平台看作一个整体时，在运动过程中速度分析如图5所示，中间矩形框代表该平台主体，两侧两个细长矩形代表该平台两侧履带，框中交叉放置斜线表示每一组辊轮接地段，为一条直线，接地段相比平台履带整体长度相比是很短的，因此可以将接地段等效为一个点。xoy为以平台中心为原点的坐标系，x'o'y'为以一侧履带中心为原点的坐标系，定义xoy坐标系与世界坐标系重合。该平台在三维空间中运动时有两个自由度，这里定义该平台运动速度为（vy，ωz）T，B为履带中心距，l为一侧履带接地长，A、A'分别为偏置角为±γ任意一组辊轮接地点，Ao为A和A'中点。

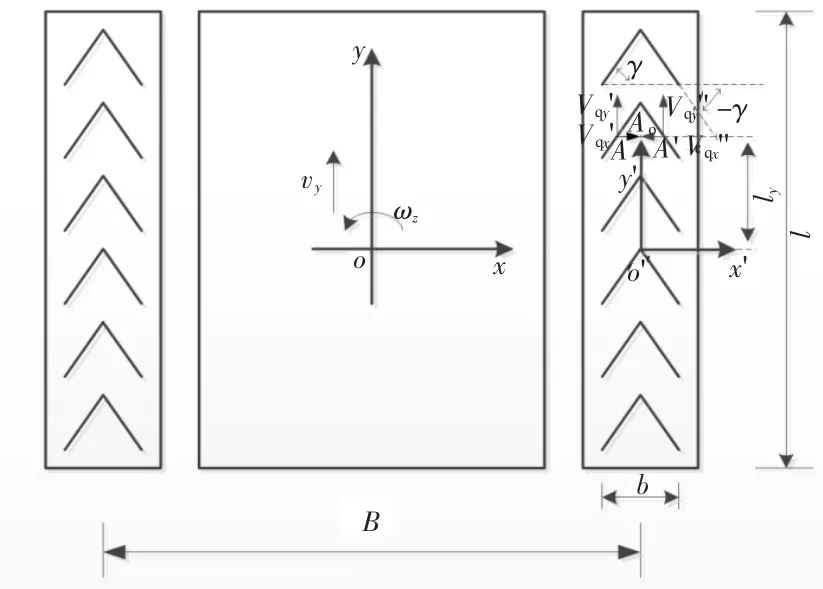
图5　平台运动速度分析

其中A点横向和纵向牵连速度分别为Vqx'、Vqy'，A'点横向和纵向牵连速度分别为Vqx''、Vqy''，定义A、A'和Ao点在x'o'y'坐标下纵坐标为ly。

设（vx'，vy'）为接地点 A 和 A'在坐标系 x'o'y'下的牵连运动速度。在A点，根据图5可得：

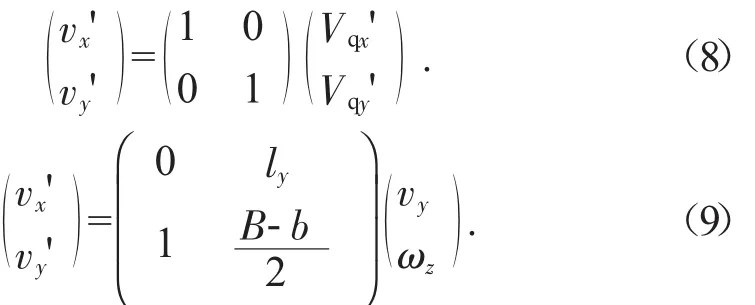
A'点，由图5得：

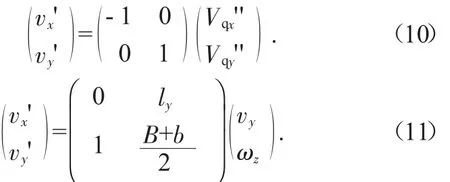
根据式（6）（8）（9）可得到A 点逆运动学方程为：

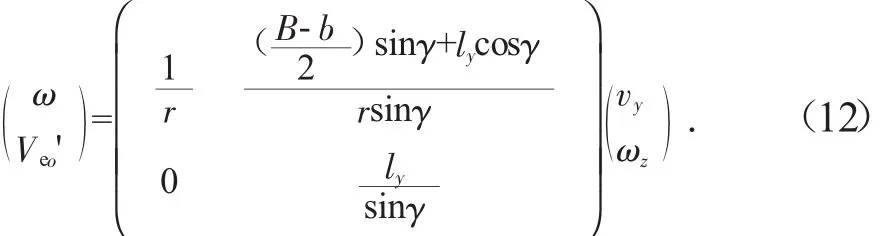
根据式（7）（10）（11）可得到 A'点逆运动学方程为：

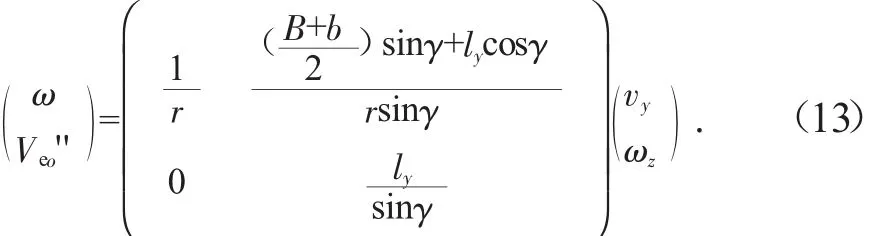
由式（12）（13）可得 A、A'接地点辊轮转速大小相等，若忽略履带板接地宽b情况下，A、A'接地点逆运动学方程为：

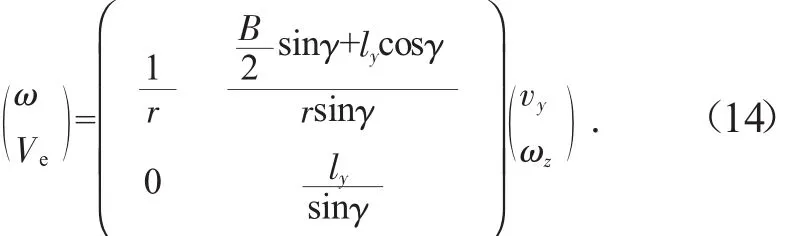
式（14）中ly为任意辊轮接地点在x'o'y'坐标系下的纵坐标，是一个变量。当平台发生转向运动时，同一侧履带上每个接地辊轮纵坐标ly均不同，导致对应的主动轮角速度以及相对于履带的运动速度也不同。在实际的运动中，每一侧履带均只有一个主动轮角速度，因此需定义以下两个函数：

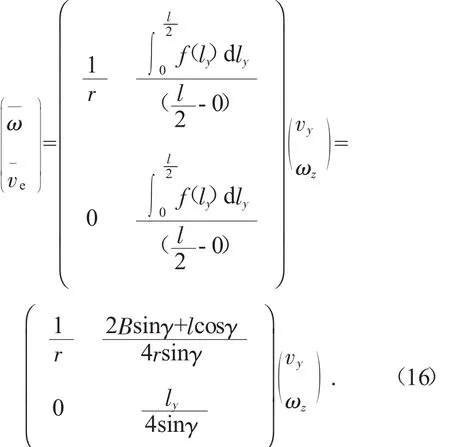
通过式（14）（16）可得，当 ly=l/4 时，式（14）、（16）完全相同，定义在一侧履带l/4处所对应的主动轮角速度和辊轮相对履带的速度为ω、ve。可得：

因此每一侧履带接地段以x轴为分割线分为两部分，每部分履带接地点均可等效在该部分履带几何中心点处，即每一侧履带的±l/4处。

该平台有两侧各有一条履带，定义每条履带上主动轮角速度分别为ω1、ω2，每一侧履带上辊轮相对于该履带的运动速度为Ve1、Ve2。因此通过式（16）（17）可以得到该平台通用的逆运动学方程为：

3　平台建模与仿真

3.1　平台在Solidworks建模

Solidworks是世界上第一个基于Windows开发的三维CAD系统，功能强大、易学易用、技术创新是Solidworks的三大优势。因此笔者利用Solidworks软件进行平台模型的建立。平台虚拟样机模型如图6所示，笔者设计的三维模型共有零部件725个，主要包括履带板、辊轮、平台主体、主动轮、负重轮、诱导轮、悬挂装置等，为了简化仿真的计算量，因此搭建的平台三维模型并没有将电机、电池、驱动装置等考虑在内。平台整体结构参数见表1。

图6　平台虚拟样机模型

表1　样机的主要结构参数

将SolidWorks中建立好的模型另存.x_t格式后，导入到Adams软件中与Simulink进行联合仿真。

3.2　平台仿真

根据式（18），将表1中平台的主要参数带入式中可得该平台的逆运动学方程为：

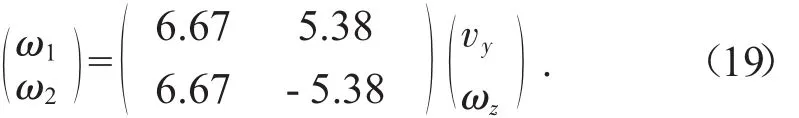
针对平台的运动性能，分别对平台的纵向直线行驶、中心转向、B/2转向运动三种运动状态进行仿真，设置两个主动轮的角速度分别为（1，1）T、（1，-1）T、（1，0.7）T，分别带入式（19）中得到该平台在两个自由度上的速度分别为（0.15，0）T、（0，0.19）T、（0.13，0.03）T，设置仿真时间为 5 s，0～0.5 s为静仿真时间，0.5～2 s为平台加速阶段，2～5s为平台稳定运动时间，得到平台的运动轨迹及速度曲线图如图7。

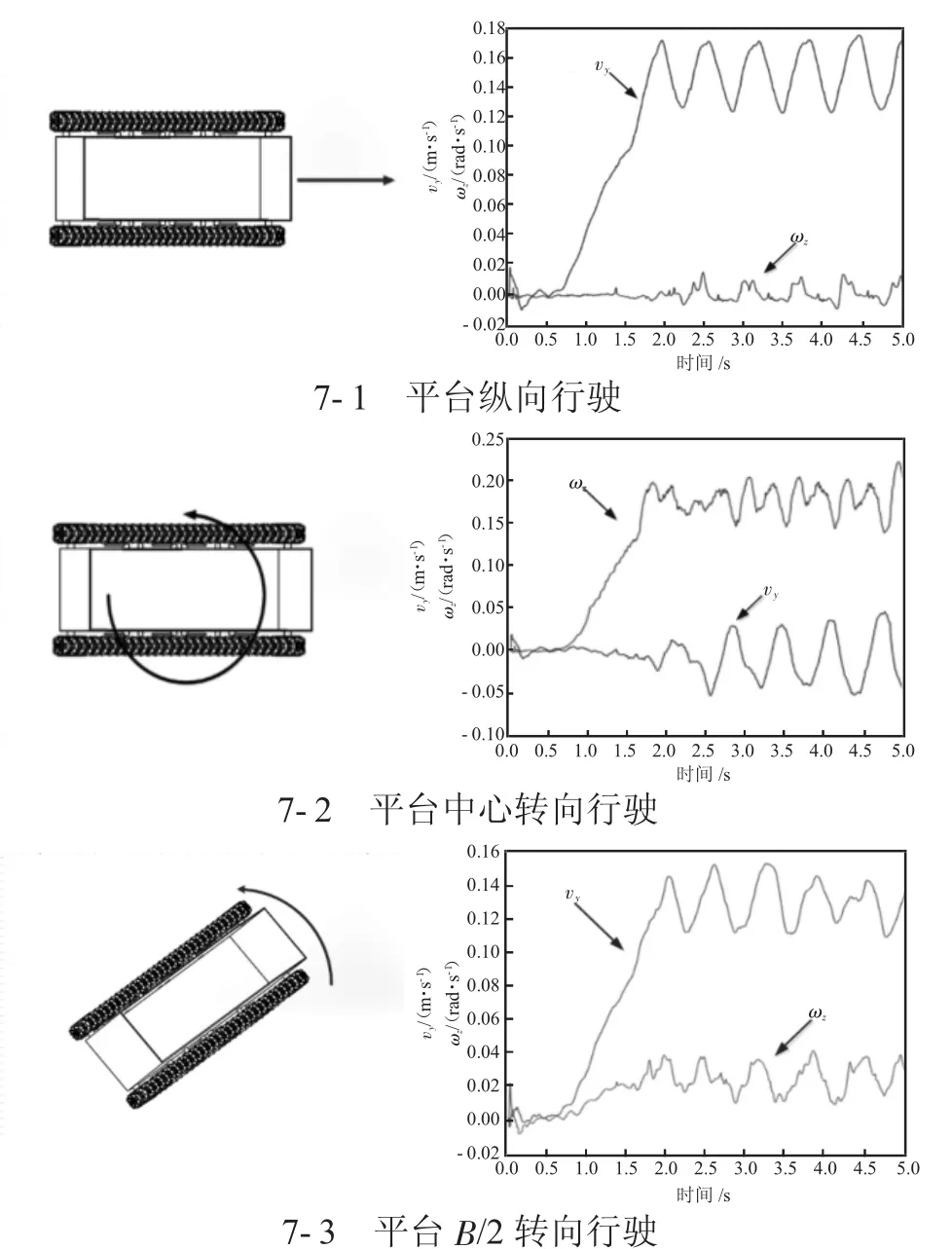
图7　平台的运动轨迹及速度曲线

仿真开始阶段，速度曲线有小幅度波动，是平台自由落体引起的微小波动，之后进入静稳定阶段。经过0.5～2 s加速阶段后平台进入较为稳定的运动状况。对稳定状况下平台的平均速度进行记录，见表2。平台在运动中存在滑移、滑转等现象会导致平台有小幅度偏移。同时运动学分析过程中忽略的平台履带的宽度对结果的影响，使平台的运动状况存在一定误差。通过表2可以看出，仿真过程所记录数据接近理论计算值。

表2　样机稳态运动平均速度

4　结论

1）对平台的纵向行驶、中心转向、B/2转向进行了运动学仿真，得到的仿真结果与理论分析值接近，验证了该平台具有一定稳定的运动性能。

2）目前只是通过仿真验证了平台的运动性能，没有通过实车行驶验证，因此实车验证为下一步的工作重点，以此验证平台具有稳定的运动性能。

3）验证该平台运动性能均在理想地面上实现的，现实中地面情况较为复杂，因此对平台在复杂路面上的行驶进行分析研究将为下一步工作的重点。

[1]张杰.履带式高效转向平台及其控制技术研究[D].北京：装甲兵工程学院，2015.

[2]郑慕窍，冯崇植，蓝祖佑.坦克装甲车辆[M].北京：北京理工大学出版社，2003.

[3]汪明德，赵毓芹，祝嘉光.坦克行驶原理[M].北京：国防工业出版社，1983.

[4]同济大学应用数学系.高等数学[M].北京：高等教育出版社，2002.