深层平板试验和单桩竖向抗压静载试验的对比分析

江小兵， 吴红兵， 张浩博

(1.中国有色金属工业西安勘察设计研究院，陕西 西安 710054； 2.西安理工大学土木建筑工程学院，陕西 西安 710048)

0 引言

据现行桩基规范[1]，干作业挖孔桩(清底干净)，中密状态的卵石、碎石其极限端阻力标准值qpk可取3300～5000 kPa，密实状态可取值到7000～11000 kPa，但从很多深层平板载荷试验的试验结果中发现，即使是密实状态的卵石层，根据深层平板载荷试验确定的极限端阻力标准值qpk很难达到4000 kPa以上，而在同一个试验场地，根据单桩竖向抗压静载试验结果反算的极限端阻力标准值qpk却可以达到7000 kPa以上。为此，本文根据Mindlin弹性理论位移积分解，使用ANSYS软件建立两种载荷试验有限元模型，通过具体算例对两种试验方法进行对比分析，并与弹性理论位移解、工程实例进行比较，从而得出一些有益于工程实践的结论，以供参考。

1 深层平板载荷试验的理论公式[2-6]

据现行《大直径扩底灌注桩技术规程》[2]，桩端下土体的沉降变形，可根据Mindlin位移解进行积分求得。

假设地面以下深度h处有一圆形均布荷载作用，圆半径为a，均布荷载大小为q，根据Mindlin位移解在圆面积上进行积分可得在自地面以下任意深度Z处产生的竖向位移为：

(1)

式中：μ——土的泊松比；E——土的变形模量。

式(1)与现行勘察规范[4]计算土的变形模量公式式(2)是完全一致的，只是式(2)是为工程应用简化的计算公式，两者均为深层平板载荷试验的理论计算公式。

E0=ωpd/s或s=ωpd/E0

(2)

式中：E0——承压板形状系数；ω——与试验深度和土有关的系数；p——p-s曲线线性段的压力；d——承压板直径；s——与p对应的压力。

因此式(1)或式(2)可与载荷板实测的竖向位移进行比较，也可建立有限元计算模型，进行比较分析。

2 深层平板和单桩竖向抗压静载试验在同等受荷条件下的有限元计算对比分析

为比较两种试验在同等受荷条件下(仅承受桩端阻力作用)的竖向位移差异，并与Mindlin位移解进行比较，以具体算例进行分析。

假设地面以下深度20 m处有一圆形均布荷载作用，圆半径为0.4 m，均布荷载大小为1000 kPa，土层变形模量为E=30 MPa，土的泊松比μ=0.3，将上述参数代入式(1)，计算桩底端圆中心线下任意深度h处产生的竖向位移s1，计算结果列于表1中。

将该计算模型输入到有限元计算软件，形成有限元计算模型1。假定直径为100 m、高为100 m的圆柱体为弹性半无限空间体，取其1/4空间对称模型进行分析。设定圆半径为0.4 m，长20 m的圆柱体为桩体，桩体模量与土体模量相同，均为E=30 MPa，泊松比μ=0.3，通过Ansys软件表面效应单元，在桩底端圆面积上施加竖向均布荷载。计算桩底端中心线下任意深度h处产生的竖向位移s1′，计算结果也列于表1中。

在有限元计算模型1中，将圆半径为0.4 m、长20 m的圆柱体去掉，并增加一个0.2 m厚刚性压板，其弹性模量值Es=2×105MPa，在刚性压板上施加1000 kPa圆形均布荷载，得到深层平板载荷试验工作条件下的有限元计算模型(模型2)，如图1所示。模型2计算桩底端中心线下任意深度h处产生的竖向位移s2，结果同样列于表1中。

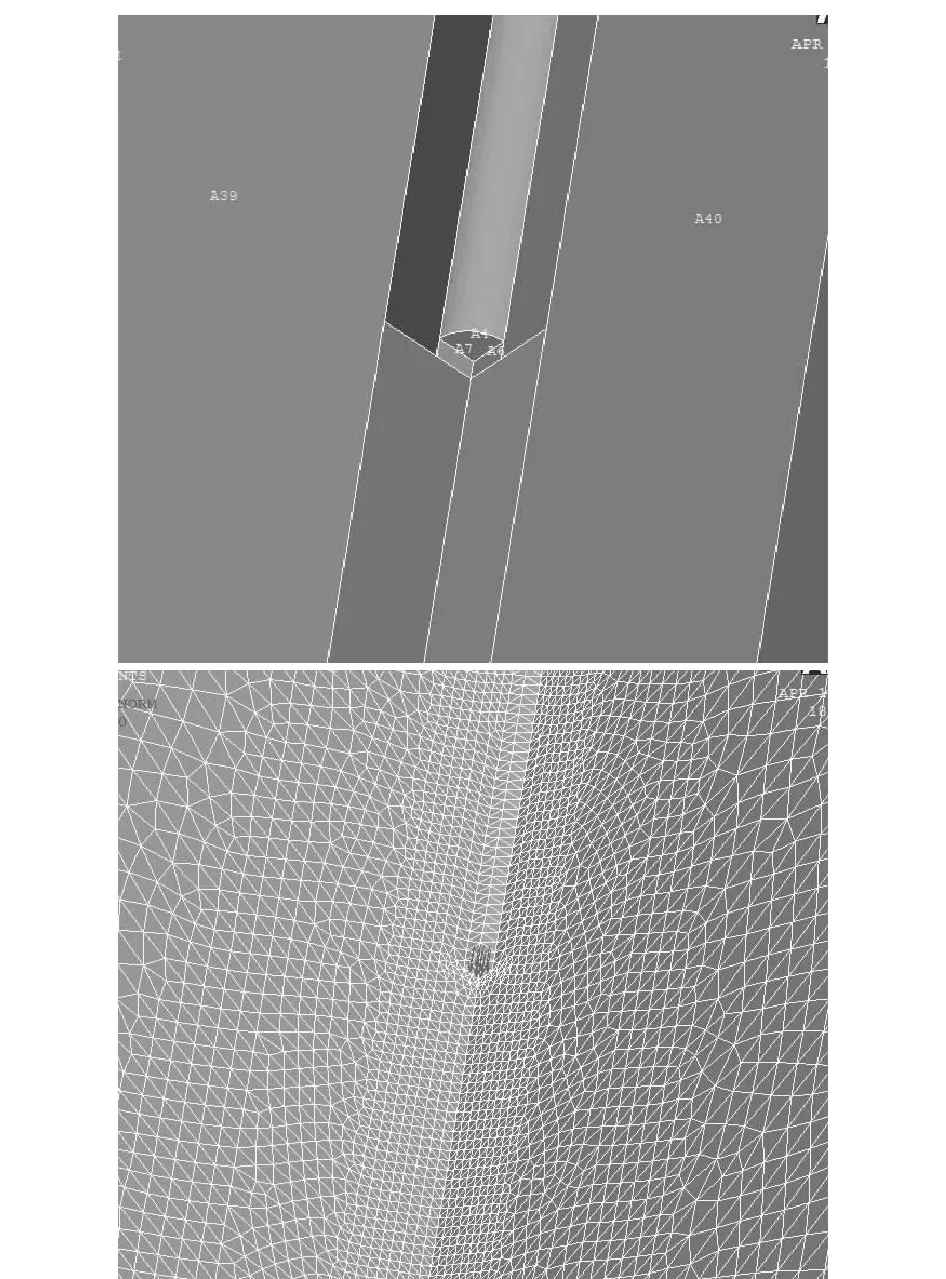
图1 深层平板载荷试验工作条件下的有限元计算模型2

在计算模型1中，将圆半径为0.4 m、长20 m的圆柱体设置成桩体材料，桩体弹性模量Es=3×104MPa，桩体与土体完全粘结，不产生相对滑移，通过Ansys软件表面效应单元，在桩底端圆面积上施加大小为1000 kPa均布荷载，得到计算模型3(设定桩侧不受侧摩阻力作用，仅受桩端阻力作用)。模型3即为单桩竖向抗压静载试验工作条件下的有限元计算模型，其计算桩底端中心线下任意深度h处产生的竖向位移为s3，计算结果同样列于表1中。

表1 桩底端中心线下任意深度h处产生的竖向位移

注：s1—完全均质地基下的Mindlin弹性理论位移解；s1′—完全均质地基下的有限元位移解；s2—有限元模拟深层平板载荷试验条件下的竖向位移；s3—有限元模拟单桩竖向抗压静载试验条件下的竖向位移。

比较计算结果s1和s1′，可以发现：在桩底下10 m范围内，采用Mindlin弹性理论位移解和有限元位移解两种计算方法的结果误差在5%以内。理论上，通过调整单元网格，s1′可以无限接近s1，由于式(1)计算的是半无限空间弹性体，而有限元计算的仅是一直径为100 m、高为100 m的圆柱体，因此两者存在一定的误差，但其精度足以满足工程需要，也可证实本文有限元计算模型的正确性。

再分析表1中数据，实际载荷试验工作中，一般只关注载荷板中心点的竖向位移，即桩底端中心点的竖向位移。从表1可看出，在桩底端中心点竖向位移s1是s3的7.1倍，s2是s3的4.6倍，它们的比值随着深度的增加逐渐减小。桩底端中心点位移s1是s3的7.1倍，说明在同等受荷条件下，完全柔性均质地基的竖向位移是桩基础的7.1倍。s2是s3的4.6倍，说明在同等受荷条件下深层平板载荷试验的竖向位移是单桩竖向抗压静载试验的4.6倍。

以下就有限元方法模拟两种试验条件下的受力机理做进一步的分析探讨。深层平板载荷试验的工作条件为桩孔开挖后，在桩底刚性承压板上施加外荷；单桩竖向抗压静载试验的工作条件为桩孔开挖浇筑混凝土成桩后，通过有限元软件表面效应单元，直接在桩端底面上施加外荷。有限元模拟两种试验条件时的加荷条件相同，都是在桩端底面上施加外荷，加荷位置与大小一样。两者的区别在于深层平板载荷试验时，由于桩孔开挖，会产生开口效应，在桩底刚性承压板施加荷载时，承压板边缘的土体会侧向挤出。图2为有限元模拟深层平板载荷试验，节点竖向位移计算结果云图，从图中可看出，承压板附近桩孔周围土体受承压板下土体的向下牵拉作用，孔壁土体向孔径方向产生位移，导致孔径收缩，从而导致承压板下土体进一步产生位移。当桩孔浇筑混凝土成桩后，桩体可抑制孔径收缩，从而抑制桩端下土体产生位移，同时也能抑制桩端边缘的土体从侧向挤出，因而在同等加荷条件下，单桩竖向静载试验产生的竖向位移会小得多。

图2 深层平板载荷试验工作条件下的土体竖向变形云图

综上分析认为，桩孔开挖产生的开口效应是导致两种试验结果产生较大差异的主要原因。

3 桩径对两种试验方式产生的竖向位移比值影响分析

对上述计算模型，笔者通过改变桩长、桩径建立多种有限元模型进行计算。结果发现，桩长对于两种试验方式产生的竖向位移比值变化不大，但桩径对于两者的比值影响较大，以下就具体算例对桩径产生的影响进行分析。

假设地面以下深度20 m处有一圆形均布荷载作用，圆直径分别为0.8、1.2、1.6、2.0 m，均布荷载大小为1000 kPa，土层变形模量为E=30 MPa，土的泊松比μ=0.3，建立有限元计算模型，分别计算深层平板和单桩竖向静载试验模型桩底端表面中心点竖向位移列于表2中。

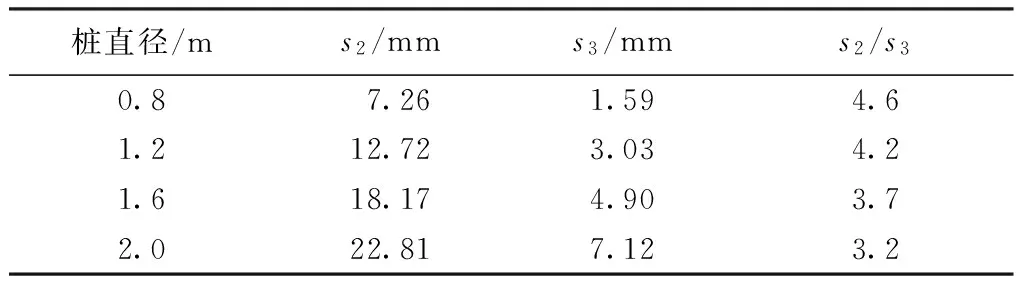
表2 桩径对两种试验条件下的竖向位移比值的影响

分析表2计算结果，可以发现，深层平板载荷试验与单桩竖向抗压静载试验，在同等受荷条件下的竖向位移比值随着桩径的增大而减小，在常规桩径0.8～2.0 m范围，两者的比值为3.2～4.6。

4 两种试验的工程实例对比

拟建场地位于某市江北片区，地貌单元属汉江左岸二、三级阶地。勘察期间未见地下水，基桩采用人工挖孔灌注桩，设计桩径0.80 m，桩端扩大头直径1.50 m，桩长10.0～15.0 m，桩端进入⑤层卵石层，桩端阻力极限值为3200 kPa，单桩竖向抗压极限承载力7000 kN。地基土岩性及性能见表3。

表3地基土岩性及工程性能

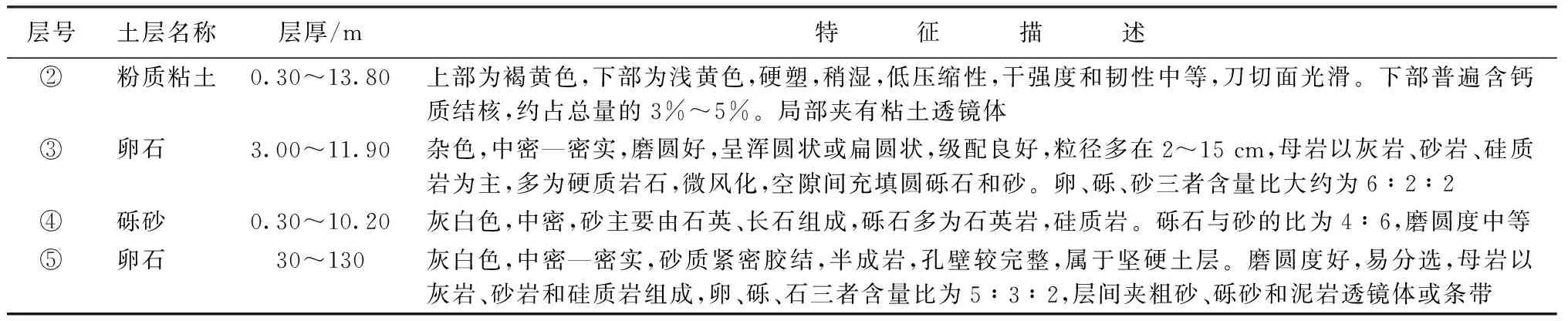
层号土层名称层厚/m特 征 描 述②粉质粘土0.30～13.80上部为褐黄色,下部为浅黄色,硬塑,稍湿,低压缩性,干强度和韧性中等,刀切面光滑。下部普遍含钙质结核,约占总量的3%～5%。局部夹有粘土透镜体③卵石3.00～11.90杂色,中密—密实,磨圆好,呈浑圆状或扁圆状,级配良好,粒径多在2～15cm,母岩以灰岩、砂岩、硅质岩为主,多为硬质岩石,微风化,空隙间充填圆砾石和砂。卵、砾、砂三者含量比大约为6∶2∶2④砾砂0.30～10.20灰白色,中密,砂主要由石英、长石组成,砾石多为石英岩,硅质岩。砾石与砂的比为4∶6,磨圆度中等⑤卵石30～130灰白色,中密—密实,砂质紧密胶结,半成岩,孔壁较完整,属于坚硬土层。磨圆度好,易分选,母岩以灰岩、砂岩和硅质岩组成,卵、砾、石三者含量比为5∶3∶2,层间夹粗砂、砾砂和泥岩透镜体或条带

为确定桩端⑤层卵石层极限桩端阻力并验证工程桩单桩竖向抗压承载力特征值是否满足设计要求，在本小区共进行了7处深层平板载荷试验和7处单桩竖向抗压静载试验，将试验结果列于表4和表5中。

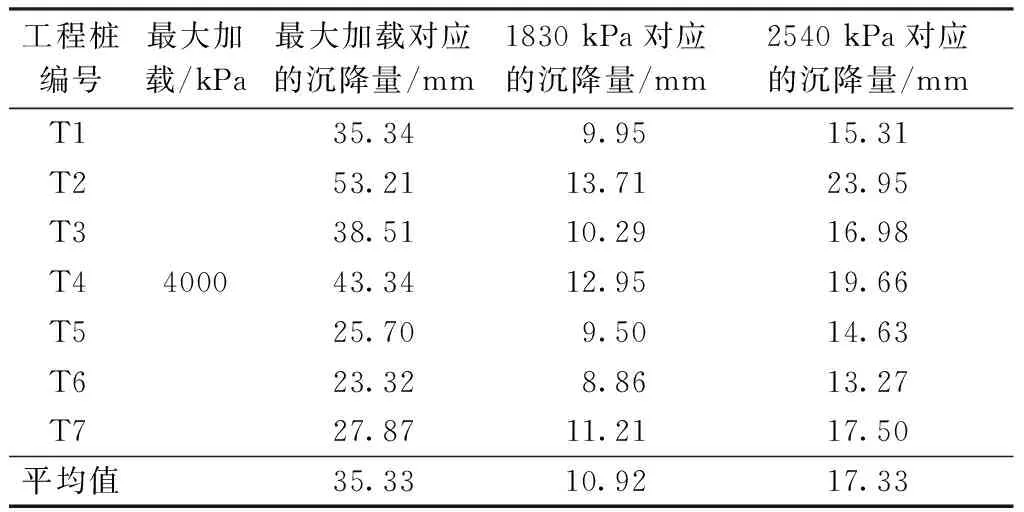
表4 深层平板载荷试验结果

表5 单桩竖向抗压静载试验结果

本小区工程桩桩长10～15 m，为摩擦端承桩，两种试验非完全同等条件，需要扣除摩擦力对桩端沉降产生的影响。据勘察报告，桩侧主要地层为④层砾砂，该层土侧摩阻力标准值为100 kPa，据此计算桩侧摩擦阻力范围为2510～3770 kN，则桩端阻力范围值为3230～4490 kN，反算扩底端桩端阻力范围为1830～2540 kPa。据表4深层平板载荷试验结果，1830～2540 kPa荷载作用下对应的沉降量范围值为10.92～17.33 mm；据表5单桩竖向抗压静载试验，扣除侧摩阻力桩端相应荷载作用为1830～2540 kPa，扣除桩身压缩变形其对应的桩端土沉降量范围值为0.84～4.22 mm，平均沉降量2.41 mm。比较两种试验结果，深层平板载荷试验与单桩竖向抗压静载试验，在同等受荷(仅受桩端阻力作用)条件下的竖向沉降均值之比值达到4.5～7.2倍。当桩径为0.8 m，根据上文有限元分析方法，两种试验方法产生的竖向位移比值达到4.6倍，具体工程实例与有限元数值计算都证实了两种试验方法产生的差异。

据表4深层平板载荷试验结果，桩端承载力特征值可取s/d=0.015所对应的荷载值，本工程可取s=0.015×800=12 mm对应的荷载值，通过插值法可得12 mm对应的荷载均值为1950 kPa，即桩端承载力特征值可取1950 kPa。据表5单桩竖向抗压静载试验结果，扣除侧摩阻力，桩端荷载平均值为2180 kPa，该荷载作用下桩端的沉降量均值为2.41 mm，该值处于p-s曲线线性段初始阶段，据线性推算，10870 kPa荷载作用下桩端的沉降量值可达12.0 mm，即桩端承载力特征值可取10870 kPa。因此单桩竖向抗压静载试验与深层平板载荷试验确定的桩端承载力比值达到5.6倍。

再根据本工程实例，将相关计算参数输入到有限元计算模型，进行有限元计算分析。据表4首先建立深层平板载荷试验有限元计算模型，桩径0.8 m，设计桩孔深12.5 m，并在桩底设置0.2 m厚刚性压板，其弹性模量值Es=2×105MPa，在刚性压板上施加2180 kPa(取1830和2540 kPa的均值)的圆形均布荷载，取土的泊松比μ=0.3。据表4中数据，为使土的平均沉降量达到14.13 mm(取10.92和17.33 mm的均值)，经有限元程序反算，可得土层变形模量为E=38 MPa。将所得土层变形模量E=38 MPa输入到单桩竖向抗压静载试验有限元计算模型，单桩桩顶承受竖向荷载7000 kN，桩长12.5 m，桩径0.8 m，扩底端直径为1.5 m，经有限元程序计算，在最大荷载7000 kN作用下对应的沉降量为18.66 mm。与表5实测结果均值相比，两者比值达到3.4倍。可见，深层平板载荷试验反算得出的变形参数是不合适的，其试验结果不能真实反映单桩竖向受力性能，根据其试验结果得出的桩端承载力值也会小很多。

5 结论

本文根据Mindlin理论弹性位移解，通过结合有限元算例，分析在同等荷载工作条件下深层平板和单桩竖向抗压静载试验的竖向位移差异。通过分析发现，在同等荷载工作条件下(仅受桩端阻力作用)深层平板与单桩竖向抗压静载试验产生的竖向位移的比值，随着桩径的增大而减小，在常规桩径0.8～2.0 m范围内，两者的比值为3.2～4.6倍，具体工程实例发现两者的比值可达4.5～7.2倍。在同等受荷条件下，工程实例揭示两者确定的桩端承载力比值可达5.6倍。

因此，深层平板载荷试验的结果不能真实反应单桩竖向受力性能，不能充分挖掘单桩竖向受力潜能，从而造成一定的工程浪费，尤其是试桩，不应采用深层平板载荷试验确定桩端承载力，而应采用单桩竖向抗压静载试验确定承载力。本文的观点是否正确，还需积累大量的工程资料证实，也希望同行专家不吝赐教。

[1] JGJ 94—2008，建筑桩基技术规范[S].

[2] JGJ/T 225—2010，大直径扩底灌注桩技术规程[S].

[3] Harry G. Poulos, Edward H. Davis.孙幼兰译.岩土力学弹性解[M].江苏南京:中国矿业大学出版社,1990.

[4] GB 50021—2001，岩土工程勘察规范(2009年版)[S].

[5] 顾宝和,周红,朱小林，等.深层平板静力载荷试验测定土的变形模量[J].工程勘察,2000，(4):1-2,6.

[6] 岳建勇，高大钊，等.再论“深层平板静力载荷试验测定土的变形模量”[J].工程勘察,2002，(1):8-10,28.

[7] 编委会.工程地质手册(第四版)[M].北京:中国建筑工业出版社，2006.

[8] 高广运，蒋建平，顾宝和，等.两种静载试验确定大直径扩底桩竖向承载力[J].地下空间，2003,23(3):272-276.