梁-板单元模型在劲性骨架钢筋混凝土拱桥仿真分析中的合理性研究

闫业祥，钱永久，谢效瑞

(西南交通大学 土木工程学院，四川 成都 610031)

有限元方法具有严密的理论基础，对于线弹性分析，当有限单元的尺寸趋于零时，有限元解将收敛于精确解[1]，因此，有限元方法被广泛应用于结构分析领域。有限元方法的误差主要来源于离散误差和建模误差[2]，离散误差和模型的数值求解有关，建模误差主要取决于结构的仿真方式以及模型的网格划分。

在劲性骨架钢筋混凝土拱桥施工阶段的仿真分析中，梁-板单元模型被广泛使用[3-9]，即劲性骨架、拱上立柱、桥面系等采用梁单元模拟，拱圈外包混凝土采用板单元模拟，板单元的厚度一般根据拱圈全截面的面积和惯性矩确定。但是关于此种模拟方式的合理性研究尚少，文献[10]对梁-板单元模型中的位移协调性进行了研究，但是所使用的结构并非实际的拱结构，而且用来验证的实体单元也只是在局部使用。因此，梁-板单元模型的合理性尚待进一步分析。

劲性骨架可看作空间桁架结构，使用梁单元模拟一般可获得足够的精度，其中钢管与管内混凝土组合后截面刚度的选取一般有3种方法[11]。对于拱圈外包混凝土，施工时一般采用分环分段不连续浇筑的方式，梁单元很难模拟该施工过程，因此宜使用板单元或实体单元进行模拟。虽然实体单元能准确地模拟拱圈的实际形状，但建模相对复杂，而且该类桥型的施工阶段分析也十分繁琐，故不应采用实体单元对整个施工阶段进行仿真分析。板单元建模简单，计算效率快，如果计算精度满足要求，可优先考虑。

本文以一座劲性骨架钢筋混凝土拱桥的主拱圈为分析对象，采用多种模型互相验证的方法，分别从结构的整体受力、局部受力和施工阶段受力3方面分析梁-板单元模型的优缺点。通过分析劲性骨架钢筋混凝土拱桥的建模误差，研究梁-板单元模型在该类桥梁仿真分析中的合理性。计算时将钢管混凝土看作一种材料，根据其应力应变关系选取组合弹性模量[12]。

1 工程概况

分析对象为一座上承式单跨劲性骨架钢筋混凝土拱桥的主拱圈，全桥整体布置如图1所示，各立柱间距均为21.2 m。主拱圈为悬链线无铰拱，净跨径为260.0 m，净矢高为50.0 m，矢跨比为1/5.2。主拱圈采用单箱双室截面，各截面横向等宽8.0 m，纵向等高4.5 m。两侧拱脚至第1根立柱间为变截面段，顶底板混凝土厚度由0.70 m线性变化至0.40 m，边腹板厚度由0.55 m线性变化至0.30 m；拱圈其余部分为等截面标准段，顶底板厚0.40 m，腹板厚0.30 m。主拱圈横截面如图2所示。劲性骨架上下弦杆均由3根φ508 mm×16(24)mm的钢管通过双角钢连接组成哑铃形断面。主拱圈采用C50自密实混凝土，劲性骨架采用Q345型钢，并在钢管内灌注C60微膨胀混凝土。

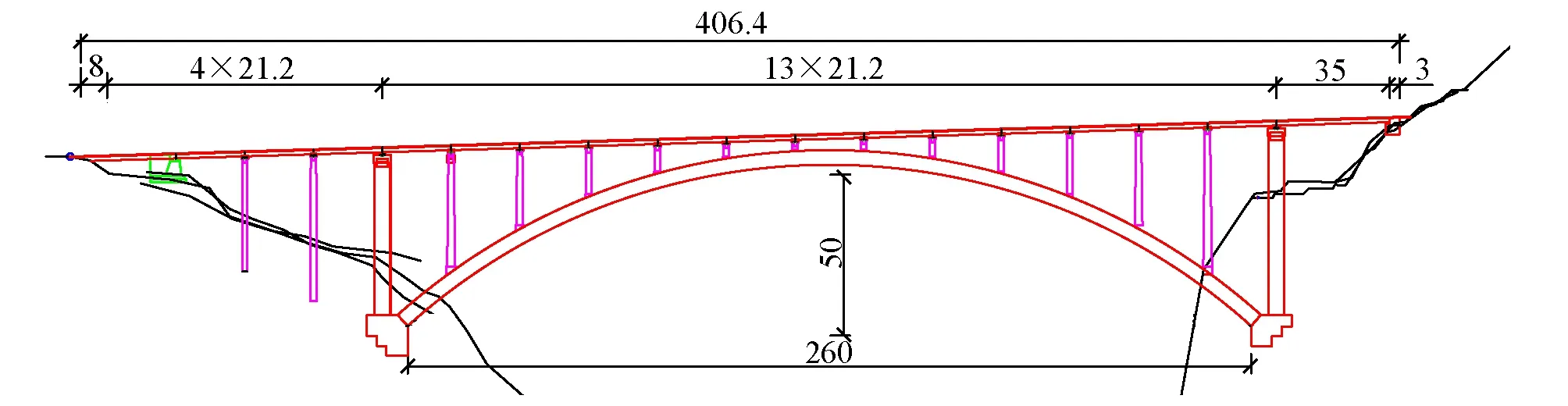
图1 全桥整体布置 (单位：m)

图2 主拱圈横截面 (单位：mm)

2 有限元模型

2.1 拱圈整体模型

利用MIDAS/Civil建立梁-板单元模型，利用MIDAS/Fea建立梁-实体单元模型。2类模型中的劲性骨架均采用梁单元模拟，区别在于分别采用板单元、实体单元模拟拱圈外包混凝土。梁-板单元模型中，采用考虑剪切变形的四边形板单元，根据全截面面积等效、整体竖向抗弯刚度等效的原则确定板厚，板梁单元共享节点。建立3种梁-板单元模型、2种梁-实体单元模型和1种单梁模型，以对拱圈整体受力行为进行比较分析。在梁-板单元模型中，板单元划分为3种尺寸：模型A为0.5 m×0.5 m；模型B为1.0 m×1.0 m；模型C为2.0 m×2.0 m。梁-实体单元模型中，全部采用六面体实体单元，尺寸为0.4 m×0.4 m×0.4 m。实体单元与梁单元之间采用刚性连接以确保劲性骨架与外包混凝土协同工作。为了比较分析，分别建立模型D(1阶实体单元)和模型E(2阶实体单元)2种实体模型。在单梁模型(模型F)中，整个主拱圈采用梁单元模拟，并忽略劲性骨架中的角钢连接系。如果所有模型的计算结果比较接近，则可认为实体单元的网格划分是可靠的。由于实体单元能准确模拟结构的实际形状，其结果可作为分析比较的标准。

计算分析时，所有模型均考虑2个荷载工况：工况1，跨中3根上弦钢管分别作用大小为100 kN且竖直向下的集中力；工况2，自重。

2.2 拱圈局部模型

为了研究梁-板单元模型在拱圈局部受力分析时的合理性，从拱脚起沿拱轴线截取长度为20 m的局部拱圈为研究对象，分别建立5个悬臂模型：模型a(梁-板单元模型，板单元尺寸1.0 m×1.0 m)；模型b(梁-板单元模型，板单元尺寸0.5 m×0.5 m)；模型c(梁-板单元模型，板单元尺寸0.25 m×0.25 m)；模型d(实体单元模型，采用1阶六面体单元，网格尺寸0.2 m×0.2 m×0.2 m)；模型e(实体单元模型，采用2阶六面体单元，网格尺寸0.2 m×0.2 m×0.2 m)。在梁-板单元模型中，劲性骨架采用梁单元模拟，拱圈混凝土采用板单元模拟；实体单元模型中，劲性骨架中的角钢连接系采用梁单元模拟，钢管采用四边形板单元模拟，尺寸为0.1 m×0.1 m，管内混凝土和拱圈外包混凝土均采用实体单元模拟。拱圈局部模型如图3所示。各模型在拱脚端部固结，在悬臂端形心位置作用一个大小为2 000 kN、方向竖直向下的集中力，以及一个大小为500 kN·m、绕截面横向形心轴的弯矩(下侧受拉)。

图3 拱圈局部模型

2.3 施工阶段模型

为了确定梁-板单元模型在施工阶段分析中的合理性，采用如下方法进行比较研究：取半跨劲性骨架主拱进行建模，分别在骨架2#立柱、4#立柱和跨中位置各浇筑一段外包混凝土，共3段6环，每段长度约4 m。采用2.1节中的梁-板单元模型C和梁-实体单元模型E，为了使计算结果更加精确，将实体单元的尺寸重新划分为0.2 m×0.2 m×0.2 m。2类模型的施工步骤完全一致，共有7个施工阶段，如表1所示。施工阶段模型以及混凝土分段分环如图4所示。

表1 施工阶段划分

图4 施工阶段模型和混凝土分环分段示意

3 拱圈整体受力行为对比分析

模型的自重与跨中挠度见表2。可知，除单梁模型外，梁-板单元模型和梁-实体单元模型的自重基本一致。由于实体单元能精确模拟拱圈的实际形状，故实体模型的自重最为精确，并以此为基准。梁-板单元模型的自重计算误差约为0.63%；单梁模型由于忽略了劲性骨架中的角钢连接系，从而导致其自重偏小。在2种工况下，各模型的跨中挠度基本处于同一范围。梁-板单元模型的跨中挠度偏大，其中板单元划分最细致的模型A跨中挠度最大，模型F的跨中挠度最小；梁-实体单元模型的跨中挠度居中。因此，可以认为实体单元的网格划分是合适的，并且实体单元能精确模拟拱圈截面的实际形状和实际刚度，可作为计算结果的基准。另外，板单元的跨中挠度偏大，反应其整体刚度偏小，使结构软化。在梁-板单元模型中，板单元尺寸越小，跨中挠度越大，而拱圈整体刚度越小。

表2 模型的自重与跨中挠度

为了对比各模型在计算主拱圈动力特性时的差别，给出其前10阶振型的自振频率见表3。可知，各模型的自振频率基本一致，其中自振频率最大的是模型F，最小的为板单元划分最细致的模型A，而模型D和模型E的计算结果居中。

表3 模型自振频率 Hz

多自由度系统的自振频率为

(1)

式中：ωn为第n阶振型的自振频率；[K]和[M]分别为体系的刚度矩阵和质量矩阵。

根据式(1)可以看出，结构的自振频率与体系的刚度矩阵与质量矩阵相关。在单梁模型F中，由于未考虑角钢连接系，模型质量较小，但截面的刚度损失并不大，故自振频率会相应提高。结合表2可知，模型A的刚度最小，质量与除模型F外的其他模型相近，故其自振频率最小。

除了自振频率外，各振型的参与质量系数也是评价结构动力特性的重要参数，它不仅可以用来判断振型属于哪个方向的平动振型或扭转振型，而且能够判断该振型在结构总反应中的参与程度。各模型的第1阶振型与第6阶振型在主要方向的振型参与质量系数见表4，其中，x方向为拱圈纵向，y方向为拱圈横向，表中未列出的方向表示振型参与质量系数为0。可知，各模型计算的振型参与质量系数基本一致，均表现出第1阶振型横向侧弯、第6阶振型纵向平动。

表4 各模型振型1与振型6主要方向的振型参与质量系数 %

根据表2—表4可知，板单元模拟拱圈外包混凝土得到的整体刚度最小，且随着板单元划分的细致程度而逐渐减小。究其原因，笔者认为在确定板单元厚度时采用了面积等效和竖向抗弯惯性矩相等的原则，且在计算板单元的面内和面外刚度时又采用了同一个厚度，造成其面内刚度比实际要小一些。考虑到有限元方法中位移元解的下限性质[1]，且使用板单元计算的误差不大，可以认为梁-板单元模型在模拟拱圈的整体刚度方面是合理的。

4 拱圈局部受力行为对比分析

根据圣维南原理选取离加载面最远的拱脚截面进行计算结果的对比分析。拱脚截面钢管正应力曲线见图5，其中钢管1-3为骨架上弦钢管，4-6为骨架下弦钢管。可知，各模型的计算结果基本一致，差别较小。一方面，说明梁-板单元共享节点的连接方式在传递应力方面是可靠的；另一方面，说明使用梁单元模拟劲性骨架是合理的。

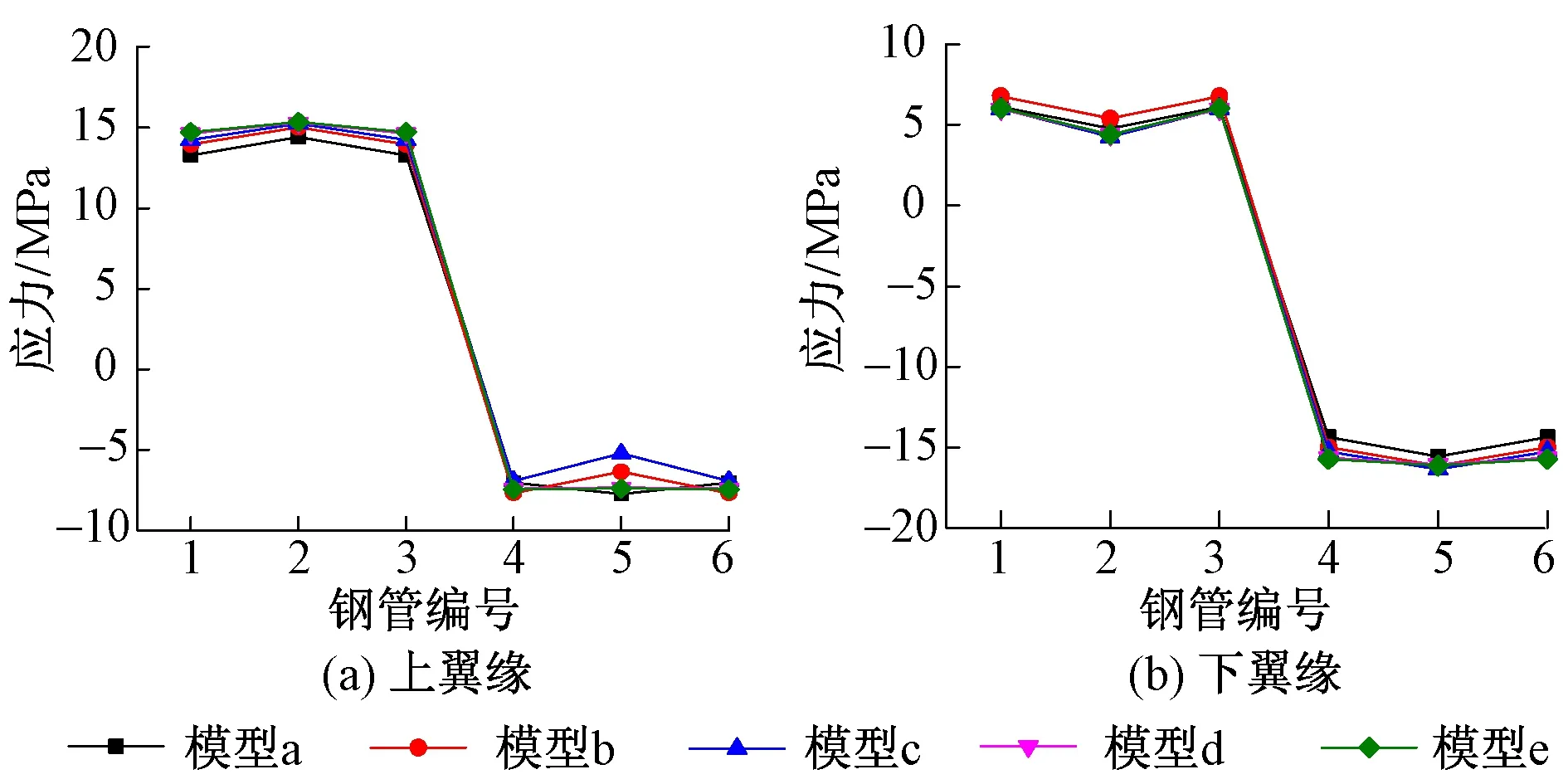
图5 拱脚截面钢管正应力曲线

在梁-板单元模型中，钢管梁单元与混凝土板单元通过共享节点的方式连接，这种连接方式只能保证二者在共享节点处保持位移与应力的协调性。在梁-实体单元模型中，钢管采用板单元进行模拟，由于钢管较薄，其单元尺寸比梁-板单元模型中的混凝土板单元尺寸要小很多，因此钢管板单元与混凝土实体单元之间存在大量的共享节点。但是无论梁-板单元模型中的混凝土板单元划分尺寸如何，其钢管梁单元与实体模型中的钢管板单元应力计算结果非常接近，因此可以得到上述结论。

拱脚截面混凝土拱轴方向应力曲线见图6，横坐标以拱圈截面中部为原点，向左为负，向右为正。可知，各模型均在截面的左右边缘达到其最大拉压应力，且其他位置的应力分布规律也基本一致。但是，梁-板单元模型的计算结果普遍比梁-实体单元模型小，以2阶实体单元模型e的计算结果为准，在左右边缘误差达到最大。模型a的最大应力误差约为13.4%，模型b的最大应力误差约为14.4%，模型c的最大应力误差约为18.8%，应力值相差0.3～0.5 MPa。另外，在梁-板单元模型中，板单元尺寸划分越细致，其应力计算结果越接近实体单元。但是，对于模型b(板单元尺寸0.5 m×0.5 m)和模型c(板单元尺寸0.25 m×0.25 m)，二者与实体单元结果的误差已非常小，说明在使用板单元模拟拱圈混凝土时，没有必要将尺寸划分的非常小。

图6 拱脚截面混凝土拱轴方向应力曲线

在梁-板单元模型中，由于板单元与梁单元共享节点，所以模型的截面宽度等于劲性骨架两侧钢管之间的中心距7.2 m，而截面的实际宽度却为8.0 m。因此，板单元无法模拟拱圈混凝土的倒角与在钢管处的挖空，但这些部位存在应力集中现象。与此相反，实体单元则能较精确地模拟存在应力集中的部位。但是与实体单元相比，板单元能够获得一个相对较好的应力计算结果，可以满足工程上的精度需要。因此，忽略这些细节部位的影响，利用板单元计算速度快、建模简单等优势，既能节省时间又能保证计算精度。

5 拱圈施工阶段受力行为对比分析

施工阶段模型自重和拱顶挠度变化曲线见图7。由图7(a)可知，在施工初始阶段与最终阶段，2个模型的自重和拱顶挠度基本一致，但是在其他阶段却有较大偏差，在CS4施工阶段误差达到最大。原因是在确定板单元厚度时，依据的是整体截面的面积等效和竖向抗弯惯性矩相等的原则，但是实际施工时截面需进行分环，这样就导致梁-板单元模型与梁-实体单元模型在激活外包混凝土的重量时出现了不一致，则截面刚度也不同。实体单元可以比较准确地模拟分环形状，板单元则受到较大的限制，这样就使得板单元在模拟外包混凝土的浇筑阶段时出现一定的误差。一种解决办法是在确定相应的板单元厚度时，将面积等效定义为截面的分环面积相等、刚度等效定义为该环对原全截面横向中性轴的惯性矩相等的原则。按该等效原则重新形成的拱圈全截面，仍能保证与原全截面的面积和竖向抗弯惯性矩相等。将依据该等效原则重新建立的模型称为修正的梁-板单元模型，其拱顶挠度计算结果列于图7(b)中，可以看出修正的梁-板单元模型挠度计算结果得到了很大改善。

图7 施工阶段模型自重和拱顶挠度变化曲线

在浇筑拱圈外包混凝土时，钢管混凝土劲性骨架仍然作为主要的受力结构，因此需要保证模型计算的应力足够精确。选取拱脚截面右侧上下2根钢管进行施工阶段轴向应力分析，应力变化曲线见图8。可知，修正的梁-板单元模型和梁-实体单元模型计算的钢管应力基本一致，修正的梁-板单元模型能满足工程上的应力精度要求。

图8 施工阶段拱脚截面钢管应力变化曲线

6 结论

1)梁-板单元模型在主拱圈整体受力、局部受力和施工阶段受力3方面具有良好的分析精度，其仿真方式是合理的。

2)利用梁-板单元模型进行施工阶段分析时，对于主拱圈的关键部位(拱脚、拱-立柱连接部位)建议采用比较小的网格尺寸，其余部位可将尺寸适当增大。

3)利用梁-板单元模型进行施工阶段分析时，应按截面的实际分环面积和该环对原全截面横向中性轴的惯性矩相等的原则共同确定对应的板单元厚度。

[1]王勖成.有限单元法[M].北京:清华大学出版社,2003.

[2]SZABO B，BABUSKA I.有限元分析的数学建模、校核与验证[M].谢宗蕻,张子龙,张勇,等译.北京:航空工业出版社,2013.

[3]杨炳成,邬刚柔,刘剑.大跨径钢管混凝土劲性骨架拱桥非线性分析[J].桥梁建设,2006，40(1):5-7.

[4]贺晓川.劲性骨架混凝土拱桥施工阶段仿真分析[D].武汉:武汉理工大学,2007.

[5]连岳泉,池瑜,贺晓川.恩施凤凰大桥施工阶段仿真分析[J].中外公路，2010,30(1):144-146.

[6]张二华,黄珍.大跨径劲性骨架钢管拱桥拱肋施工过程仿真分析[J].重庆交通大学学报(自然科学版),2013，32(1):852-855.

[7]王达,唐成,张海萍,等.大跨径CFST劲性骨架拱桥外包混凝土浇筑施工研究[J].中外公路,2016(5):67-71.

[8]邸庆辉,张健,刘山洪.劲性骨架拱桥施工过程仿真分析[J].四川建筑,2016,36(4):208-210.

[9]张富贵,张永水,董义,等.大跨劲性骨架拱桥外包混凝土浇注方案[J].重庆交通大学学报(自然科学版),2012,31(2):210-213.

[10]米曦亮,栗勇.劲性骨架在混凝土拱桥中的应用和模拟方式研究[J].城市道桥与防洪,2013(6):93-96.

[11]赵人达,张正阳.我国钢管混凝土劲性骨架拱桥发展综述[J].桥梁建设,2016,46(6):45-50.

[12]中华人民共和国交通运输部.JTG/T D65-06—2015 公路钢管混凝土拱桥设计规范[S].北京:人民交通出版社,2015.