基于CFD的大跨度邻近桥梁气动干扰效应分析
林震云,李永乐,汪 斌
(西南交通大学 土木工程学院,四川 成都 610031)
当已建桥梁不能满足日益增加的交通需求时,常在已建桥梁附近修建1座新桥或者同时修建2座邻近的桥梁来满足功能和美观方面的需求。如美国Tacoma桥[1]、日本名港西桥;我国的青岛红岛桥、佛山平胜桥、天津海河桥等。邻近桥梁距离较近时,在气流作用下上游桥面与下游桥面之间必然会相互影响,这种影响称为气动干扰效应[2]。国内外学者对不同类型钝体绕流进行了大量的试验研究和数值模拟[3-7],研究结果表明钝体之间存在气动干扰效应,对其绕流特性产生严重影响。邻近桥梁之间存在的气动干扰效应是抗风设计中的关键问题[8],特别是气动干扰效应对桥梁颤振稳定性、涡激振动、抖振以及静力风荷载的影响[9]。刘志文等[10]通过风洞试验发现双幅桥面存在明显的气动干扰效应,在涡激振动、颤振稳定性以及风荷载效应评估方面尤为突出。郭春平等[11]研究发现与单幅桥主梁的三分力系数相比,双幅桥主梁上下游三分力系数均受到一定的干扰效应。陈平、朱乐东等[12-13]针对气动干扰效应对颤振稳定性和涡振特性影响展开研究,发现计算时必须考虑气动干扰效应对颤振稳定性和涡激振动的影响。
CFD数值模拟方法能够在较短的时间内为工程前期抗风设计提供依据。根据计算流体力学基本原理,可将微分方程表示的数学模型离散为代数方程,借助FLUENT软件计算双幅桥主梁三分力系数及颤振导数。CFD数值模拟可以有效地分析邻近桥梁三分力系数的气动干扰效应,从而得到气动特性[14],为大跨度邻近桥梁气动干扰效应提供研究方法。
本文以2座大跨度桥梁为研究对象,基于CFD数值模拟方法,分析大跨度邻近桥梁的气动干扰效应,研究不同间距比和风攻角下气动干扰效应对静力三分力系数的影响,以及不同间距比和折算风速对颤振导数的影响。
1 CFD模拟与数值模型
1.1 工程背景
本文以邻近2座大跨斜拉桥为研究对象,2桥主梁中心水平距离67 m。上游桥梁全长860 m,桥跨布置为(230+400+230)m,主梁宽41 m,高4 m,主跨采用混凝土箱梁形式,见图1(a)。下游桥梁全长 1 117.5 m,桥跨布置为(57.5×2+600+57.5×4)m,主梁宽21 m,高4.5 m,主跨采用钢箱梁形式,见图1(b)。
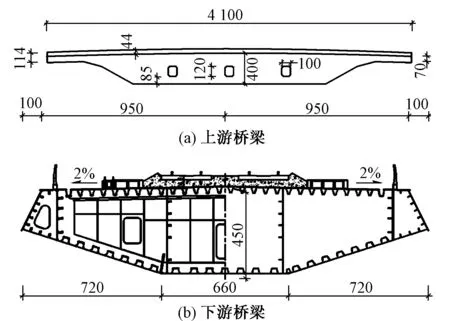
图1 主梁横截面(单位:cm)
1.2 桥面简化及数值模型
在CFD中建立精确的三维结构模型进行模拟非常困难,且对计算机配置要求很高,不仅需要投入大量的人力和物力,还需要较长的计算周期。本文根据挡风面积相同的原则将上下游桥梁主梁简化为二维模型[15],如图2所示。

图2 主梁二维简化模型
数值模拟采用基于有限体积法的FLUENT软件,在整个计算求解区域内将流体运动控制方程进行离散化求解。分析区域的大小不仅影响计算结果的精确度,而且影响数值计算的工作量。风场区域尺寸如图3所示,左侧边界为计算入口,右侧边界为计算出口。

图3 风场区域尺寸
计算入口距刚性边界网格区域7b,计算出口距刚性边界网格区域12b,左右边界尺寸为11b,其中,b为刚性边界网格区域宽度。采用该尺寸保证了顺风向的阻塞率不大于5%,满足数值风洞计算要求[15]。计算入口采用风速入口条件,计算出口采用压力出口条件,上下边界根据风攻角的正负来调整边界类型,主梁采用壁面边界。计算分析中雷诺应力项选用对复杂边界层分离流模拟比较有效的SSTκ-ω湍流模型来模拟,通过在边界条件中设置湍流强度与黏性系数来确定湍流边界条件。
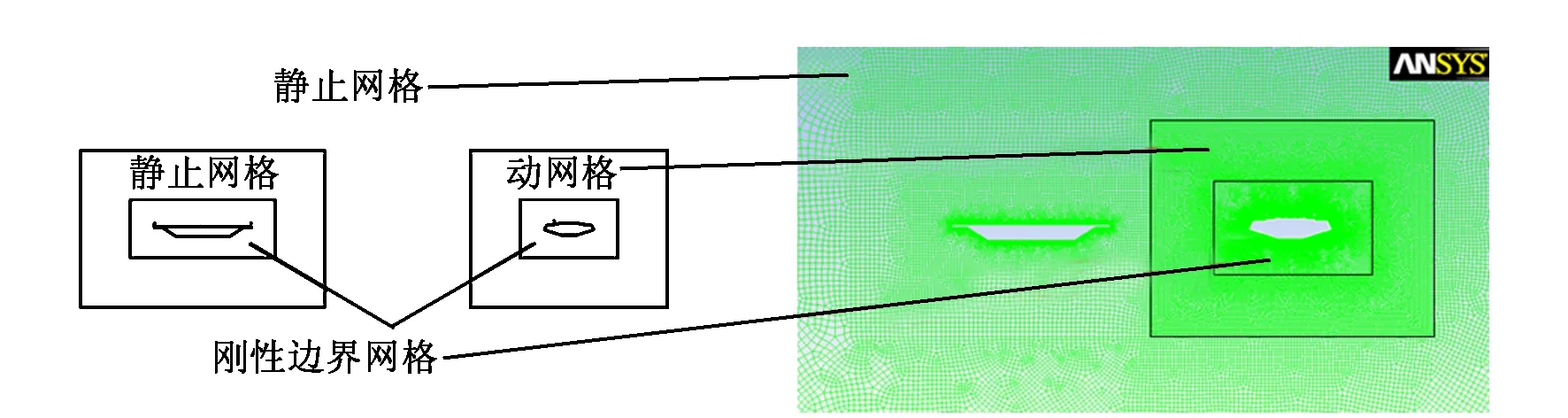
图4 模型区域划分
2 静力三分力气动干扰效应
分析静风荷载通常采用体轴坐标系和风轴坐标系,如图5所示。

图5 主梁三分力示意
在体轴坐标系下,作用在单位长度上主梁的静风荷载可表示为
(1)
(2)
(3)
式中:FH,FV,FM分别为横桥向风荷载(阻力)、竖向风荷载(升力)、扭转风荷载(力矩);ρ为空气密度;CH(α0),CV(α0),CM(α0)分别为体轴坐标系下风攻角为α0时的三分力系数;H,B分别为主梁断面的高度和宽度。
三是加强智慧河湖建设,提升河湖长制信息化水平,用新科技手段畅通公众参与和监督渠道,方便群众共建共治共享美丽河湖环境。
在风轴坐标系下,作用在单位长度上的静力风荷载阻力FD、升力FL、力矩FM仍采用上式表达,但三分力系数采用风轴坐标系下的三分力系数CD(α0),CL(α0),CM(α0)。
通过CFD数值模拟对主梁气动力进行定常分析,模拟-7°~7°风攻角下单独上游桥梁主梁、单独下游桥梁主梁以及不同间距比(D/B1=1,3,6,9)时上下游桥梁主梁断面的气动力。在风轴坐标系下,不同工况主梁三分力系数如图6所示。

图6 不同工况主梁三分力系数
2.1 气动干扰效应对上游桥梁三分力系数的影响
由图6(a)可知,由于邻近桥梁之间存在气动干扰效应,上游桥梁(D/B1=1,3,6,9)的阻力系数比单独上游桥梁主梁的阻力系数有所降低,降低程度与间距比有关,且受风攻角的影响。随着间距比的增加,气动干扰效应逐渐减弱。当D/B1=1时,阻力系数最小,受气动干扰效应影响最大。正风攻角下,当D/B1<3时间距比对阻力系数影响较大,受气动干扰效应影响较大;当D/B1>3时阻力系数对间距比变化不敏感,受气动干扰效应很小。负风攻角下,当D/B1<6时间距比对阻力系数影响较大;当D/B1>6时间距比对阻力系数几乎不产生影响。随着风攻角(绝对值)的增大,气动干扰效应对阻力系数的影响逐渐增大。-7°风攻角下气动干扰效应对阻力系数影响最大,D/B1=1的阻力系数为0.528,与单独上游桥梁阻力系数0.617相比下降了14.4%。
由图6(c)和(e)可知,上游桥梁升力系数和扭矩系数对气动干扰效应较不敏感。负风攻角时,在气动干扰效应的影响下,上游桥梁的升力系数和扭矩系数稍微提高,提高程度与间距比有关系,且受风攻角的影响。当D/B1=1时,升力系数和扭矩系数最大;当D/B1>6时,间距比对阻力系数几乎没有影响,受气动干扰效应微弱。负风攻角下,随着风攻角的增大,间距比对升力系数和扭矩系数的影响逐渐增大。-7° 风攻角下气动干扰效应对升力系数和阻力系数影响最大。
2.2 气动干扰效应对下游桥梁三分力系数的影响
由图6(b)可知,下游桥梁阻力系数受气动干扰效应明显,且与间距比和风攻角有关。随着间距比的增加,气动干扰效应逐渐减弱。风攻角在-7°~-2°和接近7°时下游桥梁阻力系数增大。风攻角在-1.5°~6.5°时下游桥梁阻力系数减小,表现出一定的遮挡效应。3°风攻角下,D/B1=1时的阻力系数为0.185,比单独下游桥梁的阻力系数0.266降低了30.5%,气动干扰效应最明显。
由图6(d)可知,气动干扰效应对下游桥梁升力系数影响很大,影响程度与间距比和风攻角有关。当D/B1=1时气动干扰效应最强,升力系数受影响最大。随着间距比的增加,气动干扰效应逐渐减弱;当D/B1>6时升力系数对间距比变化较不敏感,气动干扰效应微弱。0°风攻角下,D/B1=1时的升力系数为 -0.262,比单独下游桥梁的升力系数 -0.469 减小了44.1%。当风攻角在-7°~3°时,下游桥梁升力系数比单独下游桥梁的升力系数小。
由图6(f)可知,下游桥梁扭矩系数受气动干扰效应影响较大,随着间距比的增加,气动干扰效应逐渐减弱。当D/B1=1时影响最大,气动干扰效应最强;当D/B1>6时扭矩系数对间距比变化较不敏感,气动干扰效应微弱。
3 颤振导数气动干扰效应
颤振导数是计算颤振临界风速的依据,是桥梁的气动自激力关于运动位移与运动速率的变化率[17],表征桥梁截面在流场中运动引起周围流场变化导致气流反作用于桥梁截面的自激力特性。SCANLAN给出了颤振导数两自由度气动自激力表达式[18],如下
(4)
(5)
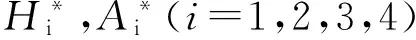
通过编制UDF(User-defined Function)让梁截面做单自由度强迫振动。假设模型分别做纯竖向或纯扭转运动并且认为梁截面刚性,竖向振动单峰幅值设为0.025B2,扭转振动的单峰幅值设为3°。采用非定常计算方法,计算在0°风攻角时不同间距比下游桥面的气动力。根据气动力时程曲线,通过最小二乘法拟合不同来流折算风速对应的颤振导数[19]。
不同工况下游桥梁颤振导数与来流折算风速的关系如图7所示。可知,邻近桥梁的气动干扰效应对下游桥梁颤振导数存在一定的影响。这种影响与间距比有关,且随来流折算风速的增大而增大。

图7 不同工况下游桥梁颤振导数与来流折算风速的关系
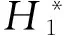
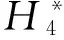



4 结论
1)上游桥梁三分力系数及下游桥梁力矩系数对气动干扰效应不敏感。
2)气动干扰效应对下游桥梁的阻力系数和升力系数的影响较为明显,影响规律与间距比和风攻角有关。
3)下游桥梁颤振导数受气动干扰效应影响较大。受间距比及折算风速的影响,不同颤振导数表现出不同的变化规律。
[1]曾华林.并行桥梁气动干扰及行车风环境[D].成都:西南交通大学,2014.
[2]KIM T,FLYNN M R.Numerical Simulation of Air Flow Around Multiple Objects Using the Vortex Method[J].Journal of Wind Engineering and Industrial Aerodynamics,1995,56(2/3):213-234.
[3]ZDRAVKOVICH M M.Review of Flow Interference Between Two Circle Cylinders in Carious Arrangements[J].Journal of Fluids Engineering,1997,99(4):618-633.
[4]ZDRAVKOVICH M M.Review of Interference Included Oscillations in Flow Past Two Circular Cylinders in Various Arrangements[J].Journal of Wind Engineering,1988,28:183-200.
[5]楼小峰,曹丰产,林志兴.串列钝体绕流的数值计算[J].同济大学学报(自然科学版),2002,30(5):604-608.
[6]陈素琴,黄自萍,沈剑华,等.两串列方柱扰流的干扰数值研究[J].同济大学学报(自然科学版),2001,29(3):320-325.
[7]刘志文,陈政清,胡建华.大跨度双幅桥面桥梁气动干扰效应[J].长安大学学报,2008,28(6):55-59.
[8]INWIN P A,STOYANOFF S,XIE J.Tacoma Narrows 50 Years Later-Wind Engineering Investigations for Parallel Bridges[J].Bridge Structures:Assessment,Design and Construction,2005,11(1):3-17.
[9]陈政清,刘光栋.桥梁风工程研究的若干新进展[J].工程力学,2006,23(增2):93-111.
[10]刘志文,陈政清,刘高,等.双幅桥面桥梁三分力系数气动干扰效应试验研究[J].湖南大学学报,2008,35(1):16-20.
[11]郭春平,白桦,洪光.双幅桥静分力系数气动干扰效应研究[J].重庆交通大学学报,2011,30(5):899-942.
[12]陈平,李小青,罗世东,等.邻近三幅桥气动干扰效应对桥梁抗风稳定性的影响[J].桥梁建设,2016,46(5):47-52.
[13]朱乐东,周奇,郭震山,等.箱形双幅桥气动干扰效应对颤振和涡振的影响[J].同济大学学报(自然科学版),2010,38(5):632-638.
[14]李素杰,彭元诚,龙晓鸿,等.连续刚构桥主梁气动特性数值分析[J].土木工程与管理学报,2011,28(3):156-159.
[15]李永乐,安伟胜,蔡宪棠.倒梯形板桁主梁CFD简化模型及气动特性研究[J].工程力学,2011,28(1):103-109.
[16]李永乐,汪斌,黄林,等.平板气动力的CFD模拟及参数研究[J].工程力学,2009,26(3):207-211.
[17]许福友.桥梁结构颤振导数识别与颤振分析[D].上海:同济大学,2005.
[18]SCANLAN R H,TOMKO J J.Airfoil and Bridge Deck Flutter Derivatives[J].Journal of Engineering Mechanics,1971,97(6):1171-1737.
[19]陈政清.桥梁风工程[M].北京:人民交通出版社,2005.

