D-S证据理论改进算法提高水下目标识别准确性*

刘标，许腾，李光

(1.海军指挥学院，江苏 南京 210000；2.海军士官学校，安徽 蚌埠 233012)

0 引言

多传感器数据融合就是人们通过对空间分布的多源信息——各种传感器的时空采样，对所关心的目标进行检测、关联(相关)、跟踪、估计和综合等多级多功能处理，以更高的精度、较高的概率或置信度得到人们所需要的目标状态和身份估计，以及完整、及时的态势和威胁评估，为指挥员提供有用的决策信息[1-2]。在复杂海洋环境下，由各种渠道获得的信息参数以及由此形成的数据库存在着不完整、不确定性，特别是模糊性。多传感器数据融合系统可以把这些模糊的、不完整的信息进行融合处理，得到一个确定的信息。本文结合水下目标识别的特点，提出一种D-S证据理论改进算法，并将其应用到水下目标识别中。

1 D-S证据理论

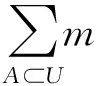
1.1 D-S证据理论组合规则

设m1和m2分别是其对应的基本概率赋值，焦元分别为A1,…,Ak和B1,…,Br，D-S证据理论组合规则定义如下[3-5]：

(1)

式中：

(2)

在式中，若K≠1，则m(C)确定一个基本概率赋值；若K=1，则认为m1和m2矛盾，不能对基本概率赋值进行组合。

1.2 D-S证据理论组合规则存在的问题

一般来说，D-S证据理论更适用于解决低冲突传感器报告的情况，而对于高冲突则会产生各种不合理的结果。这主要是因为D-S证据理论遗弃了独立焦元的每个冲突，它是基于没有任何矛盾的那部分信息构造信任结构。组合规则中K值客观地反映了融合过程中各证据间冲突的程度，0≤K≤1，K值越大，证据间冲突越激烈，矛盾越明显。

(1) 一般冲突问题

当传感器报告的基本概率赋值严重矛盾时，融合后会得到明显不合理的结果。

传感器报告1：设识别框架为U={a1,a2,a3}，有2个传感器报告的基本概率赋值给出如下：

m1：m1(A)=0.99，m1(B)=0.01；m2：m2(B)=0.01，m2(C)=0.99

。

由D-S证据理论组合规则可得：m(A)=m(C)=0，m(B)=1。尽管m1和m2对B的支持程度都比较低，但融合结果仍然认为命题B为真，这显然有悖常理。

(2) 一票否决问题。

当一条传感器报告与多条传感器报告完全不一致时，融合后出现一票否决。

传感器报告2：设识别框架为U={a1,a2,a3}，在传感器报告1中2个证据的基础上，加入第3条证据：m3：m3(A)=0.99，m3(B)=0.01。使用D-S证据理论组合规则进行融合，其结果为m(A)=m(C)=0，m(B)=1。从融合结果可以看到，增加一组证据后，对融合结果没有任何改善，出现了“一票否决”的不合理现象。

2 D-S证据理论改进算法

2.1 已有的改进算法

目前，对证据冲突问题的改进算法大体可以归为两大类：第1类算法认为：在证据高度冲突下使用D-S证据理论组合规则产生的不合理结论，是由该规则的归一化步骤所产生的。改进的组合规则主要是解决如何将冲突重新分配的问题[6-10]，典型的代表算法是Yager组合规则和孙权改进算法。第2类算法的思路是：D-S证据理论组合规则有其坚强的数学基础，本身并没有问题，在证据高度冲突时应该首先对冲突证据进行预处理，然后再使用D-S证据理论组合规则[11-15]。典型的代表算法是Murphy组合规则。

以上2类算法的争论从哲学的角度来看，当遇到“在模型X上使用算法Y获得了一个不合理的结论Z”问题时，有些学者认为是算法Y有问题，而有的则认为是模型X出了问题。这些修改算法或者将冲突完全赋给不确定元素，无法根本解决冲突证据融合的问题；或者改进算法的融合结果与融合顺序有关，不满足交换律。为此本文针对水下目标识别的特点，一方面从第1类算法出发，通过引入先验知识——传感器的可信度，修改D-S证据理论组合规则降低冲突因子K值；另一方面，吸收了第2类算法的特点，通过可信度对传感器报告进行预处理，保证融合结果的合理性。

2.2 D-S证据理论改进算法

根据经验对一个事物或现象为真的相信程度称为可信度。本文通过引入可信度，定量地反映被融合信息的质量，可信度高的信息赋予较高的权值，可信度低的赋予较低的权值，这样便增加了正确信息的优势，削弱了错误信息对最终结果的影响，有效地减少了系统的不确定性。确定传感器可信度的方法通常有2种：一是根据传感器本身的工作性能，对其进行长期的测试积累或者多周期的循环测量，通过统计试验将传感器的识别结果与真实水下目标进行比较，计算其识别准确率作为信任度；二是由相关领域专家根据以往的实践及经验给出。

通过可信度对传感器报告进行预处理，将传感器报告在可信度上进行重新分配。假设有2个传感器，它们的可信度分别记为R1和R2，m1和m2分别是其对应的基本概率赋值，焦元分别为A1,…,Ak和B1,…,Br。首先将焦元A1,…,Ak和B1,…,Br在可信度R1和R2上进行重新分配，把1-R作为未知信息分配给识别框架U，而后用D-S证据理论组合规则进行计算，则得D-S证据理论改进算法为

(3)

式中：

(4)

2.3 融合结果比较

下面使用上文提到的典型改进算法和本文的D-S证据理论改进算法对传感器报告1和传感器报告2进行计算。设传感器A,B,C的可信度分别为RA=0.85，RB=0.3，RC=0.9。使用Matlab软件进行编程计算，融合结果如表1所示。

由表1可以看出，本文的改进算法在解决两证据高度冲突和一票否决的问题上明显优于以前的各种算法。Yager组合规则虽然把冲突的证据完全

否定了，但把支持证据冲突的那部分概率全部赋予了未知信息U，随意抛弃了信息，使得算法过于保守。而Murphy组合规则由于只是对证据进行简单算术平均，没有考虑到各参与合成证据的可信度。孙权改进算法没有完全否定冲突证据，但所得结果只有0.182 1及0.336 7，与常理有一定的差距。本文的D-S证据理论改进算法加入了传感器报告的可信度，使可信度高的传感器报告得到了较高的基本概率赋值，消除了D-S证据理论在解决冲突问题时可能产生的与直觉相悖的结果的问题。加入第3条证据后，a1的基本概率赋值得到了明显的提高，达到了0.976 1，而未知信息U却降低到了0.015 1，改变了证据失效的问题。

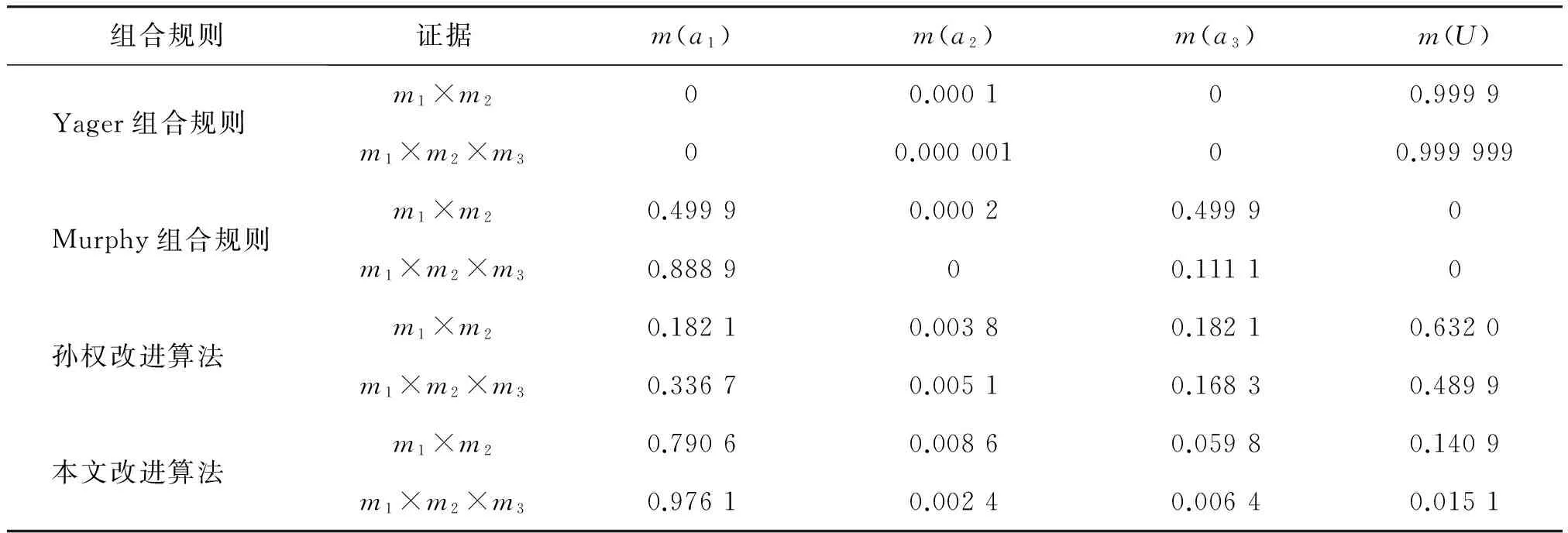
表1 几种组合算法的融合结果

3 传感器报告

3.1 传感器报告形式

根据各种传感器提供的信息互补的原则，我们选取多个声呐传感器、磁感应传感器、水压传感器构成多传感器数据融合系统。在D-S证据理论中，传感器报告以基本概率赋值的形式给出。设水下目标识别框架为U，识别框架内有n个元素，融合系统内共有G个传感器向融合中心报告，则传感器报告的形式如下：

Sg=[mg1:mg2:…:mgn],g=1,2,…,G，

(5)

式中：g为传感器下标；mg1，mg2，…，mgn表示水下目标识别框架内n个元素的基本概率赋值。

3.2 传感器结果判定准则

对融合结果进行决策的方法有基于信任函数的决策、基于基本概率赋值的决策和基于最小风险的决策。基于信任函数的决策根据组合后得到的m，求出信任函数BEL，则该信任函数就是判决结果，这实际上是一种软判决。基于最小风险的决策是求决策集中最小者为最优决策。根据水下目标识别的计算过程及传感器报告的形式，本文采用基于基本概率赋值的决策[2]，其规则如下：

设∃A1,A2⊂U，满足

m(A1)=max{m(Ai),Ai⊂U}

，

(6)

m(A2)=max{m(Ai),Ai⊂U且Ai≠A1},

(7)

若有：

(8)

则A1即为判决结果，其中ε1，ε2为预先设定的门限，即：

(1) 识别出的水下目标应具有最大的基本概率赋值；

(2) 识别出的水下目标的基本概率赋值与框架内其他水下目标的基本概率赋值的差必须大于某一阈值；

(3) 不确定性区间长度必须小于某一阈值；

(4) 识别出的水下目标的基本概率赋值必须大于不确定性区间长度。

4 D-S证据理论改进算法在水下目标识别中的应用

4.1 传感器报告

假设在某一海域，由声呐传感器、磁感应传感器、水压传感器等多种构成多传感器数据融合系统进行水下目标探测，识别框架为U={a1,a2,a3,a4,a5}，a1表示该水下目标是1类舰船，a2表示该水下目标是2类舰船，a3表示该水下目标是3类舰船，a4表示该水下目标是4类舰船，a5表示该水下目标是5类舰船。假设有4个传感器，每个传感器均有一个可信度，分别为R1=0.96；R2=0.84；R3=0.75；R4=0.92。每个传感器在探测到目标后产生一个传感器报告送至融合中心，这些报告给出如下：

来自传感器1的报告：

S1= [m11:m12:m13:m14:m15]=

[0.17:0.46:0.10:0.04:0.23];

来自传感器2的报告：

S2= [m21:m22:m23:m24:m25]=

[0.36:0.22:0.12:0.17:0.13];

来自传感器3的报告：

S3= [m31:m32:m33:m34:m35]=

[0.04:0.42:0.20:0.26:0.08];

来自传感器4的报告：

S4= [m41:m42:m43:m44:m45]=

[0.24:0.34:0.16:0.10:0.16].

4.2 融合计算

在融合中心，将传感器的报告代入公式(3)，使用MatLab软件进行编程计算，可以求得各传感器融合后的基本概率赋值如表2所示。

表2 传感器报告的融合结果

图1通过将融合结果与原传感器报告进行对比，直观地反映出了D-S证据理论改进算法的融合效果。

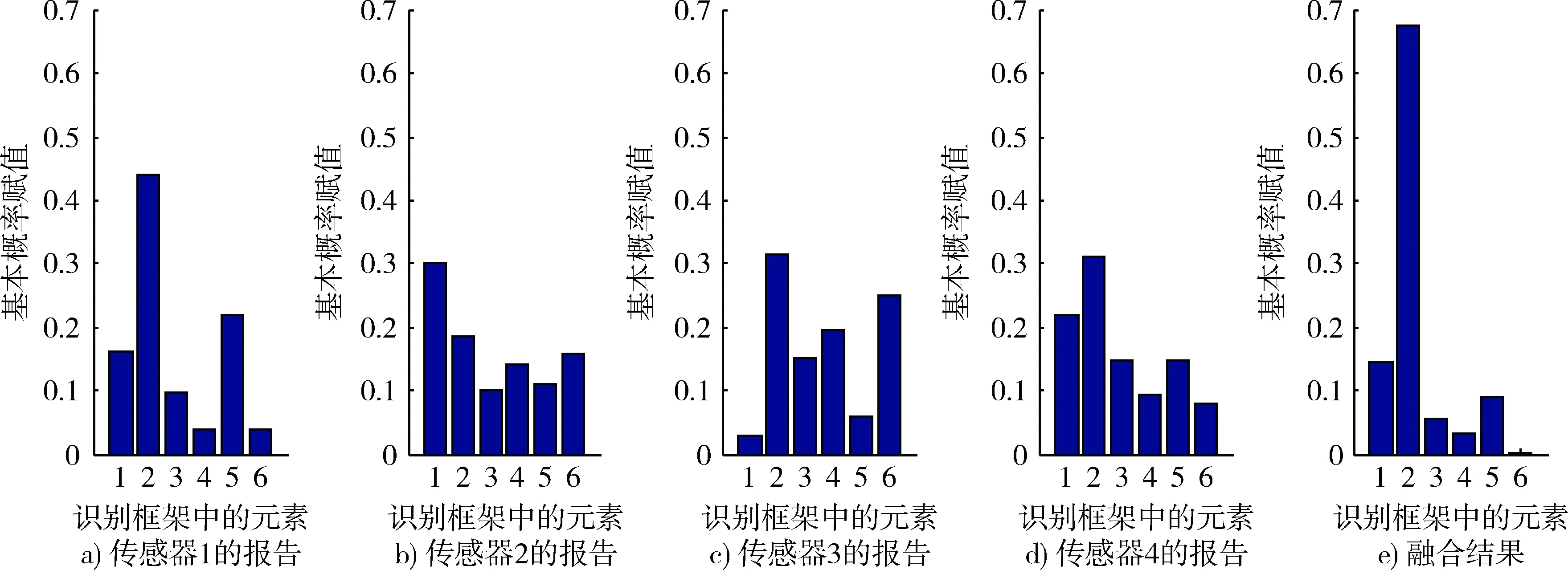
图1 各传感器报告与融合结果对比图Fig.1 Comparison of sensor reports and fusion results

4.3 结果判定

根据基于基本概率赋值的决策进行判定，最终融合结果满足

m(a2)=0.677 1=max{m(ai),ai⊂U}

,

m(a1)= 0.143 5=max{m(ai),

ai⊂U且a1≠a2},

式中：ε1，ε2为预先设定的门限，若选择ε1=0.35，ε2=0.1则最终的判定结果是a2，即识别的目标是2类舰船。

5 结束语

采用水下传感器的目标识别技术在现代海战中得到广泛的应用，在海洋的舰船目标的侦查与监视中，能否对水下目标实现正确的检测和分类，对于海军舰艇的作战能力和生存能力至关重要，因此，迫切需要水下传感器能够自动检测和识别目标。在复杂海洋环境中，使用多个传感器，采用数据融合技术对多源信息进行融合处理，就可以比较容易地实现对水下目标的识别。而D-S证据理论不失为一种有效的信息融合目标识别手段。本文引入可信度，对D-S证据理论进行了改进，对于不确定的多源信息，得出了确定的正确的结果，结果表明，该方法提高了数据融合系统的有效性，使整个系统的性能得到进一步改善。

[1] 杨万海.多传感器数据融合及其应用[M].西安：西安电子科技大学出版社，2004. YANG Wan-hai.Multi-Sensor Data Fusion and Application[M].Xi′an:Xidian University Press，2004.

[2] 曾志勇, 王宝树, 李芳社.数据融合中的辐射源识别技术[J].西安电子科技大学学报,1999,26(4):462-465. ZENG Zhi-yong,WANG Bao-shu,LI Fang-she.Radiation Source Identification Technology in Data Fusion[J].Journal of Xidian University,1999,26(4):462-465.

[3] 何友,王国宏.多传感器信息融合及应用[M].2版.北京:电子工业出版社,2007. HE You,WANG Guo-hong.Multi-Sensor Information Fusion and Application[M].2nd ed.Beijing:Electronic Industry Press，2007.

[4] LLINAS J,WALTZ E.Multisensor Data Fusion[M].Norwood,MA:Artech House,1990.

[5] 彭冬亮，文成林，薛安克.多传感器多源信息融合理论及应用[M].北京:科学出版社,2010. PENG Dong-liang,WEN Cheng-lin,XUE An-ke.Multi-Sensor Multi-Source Information Fusion and Application[M].Beijing:Science Press，2010.

[6] DUBOIS D,PRADE H.A Survey of Belief Revision and Updating Rules in Various Uncertainty Models[J].International Journal of Intelligent Systems,1994,9(6):61-100．

[7] YAGER R R.On the Dempster-Shafer Framework and New Combination Rules[J].Information Sciences,l987,41(2):93-138.

[8] TAZID A,PALASH D,HRISHIKESH B.A New Combination Rule for Conflict Problem of Dempster-Shafer Evidence Theory[J].International Journal of Energy,Information and Communications,2012,3(1):35-40．

[9] 孙全,叶秀清,顾伟康.一种新的基于证据理论的合成公式[J].电子学报,2000,28(8):117-119． SUN Quan,YE Xiu-qing,GU Wei-kang.A New Formula Based on New Evidence Theory[J].Journal of Electronics,2000,28(8):117-119．

[10] YANG Yi,HAN De-qiang，HAN Chong-zhao.Discounted Combination of Unreliable Evidence Using Degree of Disagreement[J].International Journal of Approximate Reasoning,2013,54(8):1197-1216．

[11] 刘海燕,赵宗贵,刘熹.D-S证据理论中冲突证据的合成方法[J]．电子科技大学学报，2008，37(5):701-704． LIU Hai-yan,ZHAO Zong-gui,LIU Xi.Combination of Conflict Evidences in D-S Theory[J].Journal of University of Electronic Science and Technology of China,2008,37(5):701-704.

[12] DENG Yong,SHI Wen-kang,ZHU Zhen-fu,et al．Combining Belief Functions Based on Distance of Evidence[J].Decision Support Systems,2004,38(3):489-493．

[13] 胡海亮，钟求喜，刘浏.基于迭代合成的D-S证据理论改进方法[J].计算机应用研究,2016,33(10):2985-2987. HU Hai-liang，ZHONG Qiu-xi，LIU Liu.Improved Method to D-S Evidence Theory Based on Iterative Synthesis[J].Application Research of Computers,2016,33(10):2985-2987.

[14] MURPHY C K.Combining Belief Functions When Evidence Conflicts[J].Decision Support Systems,2000,29(1):1-9.

[15] 唐克，谢保军，王奇.基于D-S证据理论改进算法的末敏弹多传感器融合技术研究[J].舰船电子工程,2012,32(4):43-44. TANG Ke,XIE Bao-jun,WANG Qi.Research on Terminal-Sensitive Projectiles Multi-Sensor Amalgamation Technology Based on Advanced Evidence Theory[J].Ship Electronic Engineering,2012,32(4):43-44.