杭州湾中部波浪统计分布

杨 斌，叶 钦，张俊彪，周 阳

(国家海洋局第二海洋研究所 工程海洋学重点实验室， 杭州 310012)

河口海湾波浪受风、地形、水流、涨落潮等众多因素影响，其统计分布特性一般与沿海波浪有所不同，较为复杂，而且河口海湾工程历来重视波浪的影响，因此，对河口海湾的波浪进行分析研究是非常有必要的。杭州湾为喇叭形海湾，上有钱塘江水流入，同时受潮汐影响，湾内水深总体上南浅北深，其中有不少小岛和浅滩，湾口有舟山群岛为屏障，对外海灾害性波浪具有明显的阻挡效应。根据浙江省海岛资源综合调查与研究得知，浙江沿海波浪具有较为明显的季节性，即冬季大，夏季小，较大波浪为台风引发，其次为寒潮，浙北沿海波高相对小于浙南，常浪向以偏北向为主，夏季波浪以偏南向为主。与浙江沿海气象相似，杭州湾中部冬季受偏北风影响，冷空气影响频繁，持续时间长，夏季受偏南风影响，其中朝北上的台风影响较大。对湾内实测波浪进行研究有助于深入了解杭州湾的波浪特性，同时也对湾内的灾害性波浪的预防也有较为实用的价值。

国内对河口实测波浪进行研究分析的论文主要关注于波浪的消减以及波谱和波周期的变化(王以谋 等[1])，或者对河口波浪的谱特性作分析(冯卫兵等[2])，也有对杭州湾的波浪特性进行统计分析的论文(茹荣忠等[3]，张伯虎等[4])，而对杭州湾中部的波高分布或者波周期分布研究未见报道。对于波浪分布的分析主要是近岸海域的研究较多(束芳芳等[5]；郭浩霖等[6])，河口型海湾的分析报道甚少。

对波浪进行统计分布分析需要用到波浪统计分布理论，常用浅水理论波高分布主要有考虑相对水深为主要参数的Gluhovski分布[7]和基于墨西哥湾飓风浪资料提出的威布尔分布[8]，这两者应用广泛。由于波周期分布较窄，似乎与水深关系不明显，因此，适用于深水的理论周期分布亦可以用于浅水，主要有孙孚分布[9]和近些年根据浅水因子和波陡参数推导出来的Hou Yijun分布[10]。

本文利用杭州湾中部一年的实测波浪资料，统计分析了杭州湾的波高分布、波周期分布和联合分布特性，采用多种理论分布进行对比分析，运用最小二乘法拟合实测分布，并探讨了分布公式中的系数与相对水深、波陡等参数的关系。

1 数据和方法

1.1 数据介绍

波浪资料采用声学多普勒流速剖面仪(Acoustic Wave and Current profiler，简称AWAC，中文名称浪龙)进行测量收集，仪器利用声表面追踪方法测波，亦能同步分层测流速和流向，所测数据经过仪器配套的Storm处理软件可计算波高、周期、波向、水深、流速、流向等参数以及波谱等数据，测量所得数据可靠，精确度高。

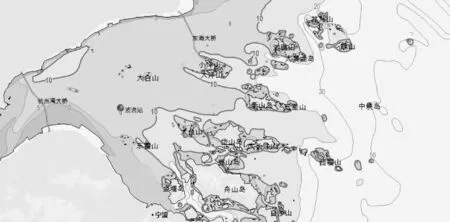
图1 波浪观测站位置示意图Fig.1 Location of wave station

本次研究的测波点位于杭州湾中部，经纬度位置为121.577°E, 30.387°N(图1)，实际水深约为10 m。测量时仪器设置为每一小时记录一次波面，一次记录2 048个波面数据，波面记录采样间隔设为0.5 s，测量时长为1 a，自2009-06-01～ 2010-05-31。

1.2 数据处理和统计

将波面数据进行中心化和消除趋势项处理，得出均值为零的波面数据，对波面数据中有明显不合理波动的数据组进行了删除处理，确保了数据有效性，得到7885组数据可用；随后采用上跨零点法统计单个波高和单个波周期，统计计算实测波高分布和波周期分布，并计算平均波高Hm、平均周期Tm、谱宽度和相对水深等参数；谱宽度ν根据频率谱计算，频率谱是运用快速傅里叶变换方法计算，自由度为32，谱高频截断为1 Hz。

统计得出，平均波高变化范围为0.03～1.35 m，年均值0.29 m；平均波周期变化范围为1.6～5.4 s，年平均值为2.9 s；谱宽度ν的变化范围为0.22～0.92，年均值0.39；相对水深(平均波高除以水深)为0.24～2.66，均值为0.88。一年之中最大的两个波浪过程为8月6日至11日的台风浪过程和11月15日至18日的冷空气过程。受2009年第8号莫拉克台风影响，该过程波向自东北向顺时针转向偏南向，主要波向为偏东向，出现最大十分之一波高为2.17 m，对应平均周期为3.9 s。11月的最大波浪过程波向主要为偏北向，出现最大十分之一波高为2.72 m，对应平均周期为5.5 s。

对实测资料的波高分布进行统计分析时，将波高以平均波高进行无量纲化，得到无量纲波高h=H/Hm，实测波高直方图的区间间隔取△h=0.1，统计在(h,h+△h)区间内出现的波个数，除以总波数和△h，即可得到波高在该区间的概率密度，有多组数据就将各区间的多组数据的概率密度相加之后取平均值，得到各个区间的平均实测波高概率密度分布，在统计计算实测波周期分布时亦按此方法。

2 理论分布

2.1 波高分布

常用浅水理论波高分布主要有Gluhovski分布[7]和威布尔分布[8]，拟合时对于Gluhovski分布采用的相对水深采用平均值。具体公式如下：

(1)Gluhovski分布。考虑到水深对波高的影响，通过对浅水波高分布的系统分析，Gluhovski得出如下经验概率密度分布

(1)

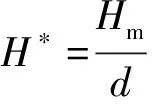
(2)为方便比较分析，进行Weibull拟合时采用如下模式

(2)

2.2 周期分布

波周期分布用威布尔分布、孙孚分布[9]和Hou Yijun分布[10]来拟合，Hou Yijun分布为近些年出现的理论分布，拟合时涉及到的浅水因子和波陡等参数均采用平均值。威布尔分布公式与波高分布中提及的一致，其他公式如下：

(1)孙孚分布。孙孚利用波动的射线理论得到了一种更符合实际结果的波周期分布形式

(3)

式中：τ=T/Tm。

(2)Hou Yijun分布。 Hou Yijun分布考虑了波浪的非线性影响

(4)

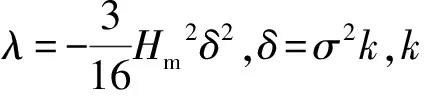
3 拟合分析

3.1 波高

利用7885组数据进行统计得到实测波高概率密度直方图，并由各理论分布拟合实测直方图得出拟合曲线，具体见图2。从图2可见，(1) 绝大部分实测波高分布在平均波高3倍范围内，最大概率出现的波高是平均波高的0.8～0.9倍; (2) Gluhovski分布曲线在概率密度最大值及其附近稍左偏于实测值，小波高比区域与实测较为符合，过最大概率密度值之后曲线先偏低于实测值后又在较大波高比部分高于实测值; (3) 相对而言，威布尔分布曲线整体拟合效果好于Gluhovski分布，拟合得到系数α和β分别为2.16和0.75。

3.2 周期

与实测波高分布统计计算类似，经统计得到实测波周期分布直方图及各理论分布拟合曲线见图3。由图3可见，(1) 实测波周期分布主要集中在平均周期2.5倍范围内，最大概率出现的周期是平均周期的1.0～1.1倍; (2) 孙孚分布曲线的最大概率密度值偏左于实测值，小周期比部分偏小，大周期比区域偏大；(3) Hou Yijun分布曲线在小于1.4倍的周期比区域总体上偏低于实测值，在大周期比区域与孙孚分布相似，高于实测值。(4) 威布尔分布曲线在两端偏低于实测值，最大概率密度处偏小，但附近区域则稍大于实测值，拟合得到系数α和β的值分别为3.79和0.67。

用威布尔分布拟合实测波高分布得出分布系数α的变化范围和均值为1.61～2.75(2.17)，分布系数β的变化范围和均值为0.58～0.92(0.75);用威布尔分布拟合实测波周期分布得出分布系数α的变化范围和均值为1.75～9.38(4.07)，分布系数β的变化范围和均值为0.29～1.60(0.67)。拟合的波高分布系数均值与经典的瑞利分布(α=2，β=0.79)并不一致，而且与石臼港沿海的拟合数据(α=2.25，β=0.74)[11]也不相同，周期分布的拟合系数也与沿海海域(α=3.11，β=0.59)[11]的不一样，说明波浪的分布有区域性特点。

3.3 联合分布

根据波记录中单个波高与平均波高之比，以及单个波高对应周期与平均波周期之比统计计算出实测波高周期联合分布，并与孙孚提出的理论联合分布进行比较分析，见图4。由图4可见，实测联合分布的高发生概率区域(发生概率密度大于0.9)位于波周期比0.5～1.5和波高比0.2～1.5之间。实测联合分布在整体形状上与孙孚联合分布是有区别的；实测分布的高概率密度区域右偏于孙孚分布的高概率区域，而且实测分布的高概率区域范围要大于孙孚分布的高概率区域；实测分布与孙孚分布在小波高比和小周期比区域的等高线有相似的分布，但是其他区域则趋势不一致。

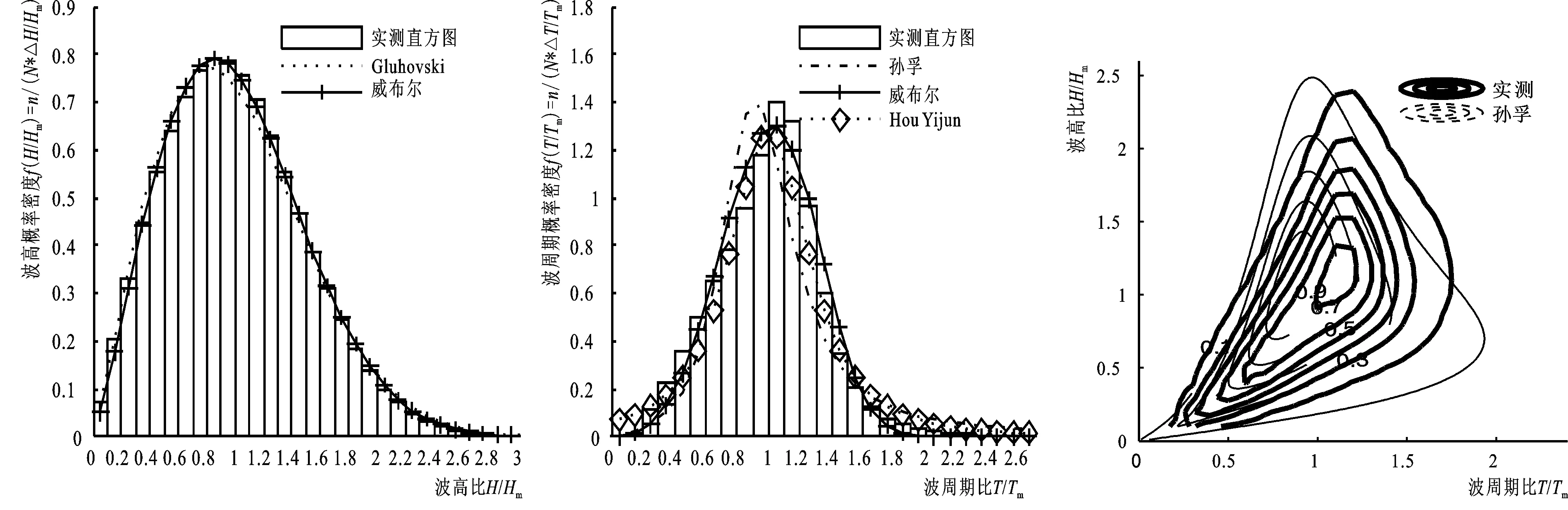
图2 平均实测波高分布与理论拟合分布曲线Fig．2Distributionofmeasuredmeanwaveheightandtheory图3 平均实测波周期分布与理论拟合分布曲线Fig．3Distributionofmeasuredmeanwaveperiodandtheory图4 平均波高和平均周期联合分布与孙孚分布等高线Fig．4ThejointdistributionofmeasuredmeanwaveheightandwaveperiodandSunfutheory

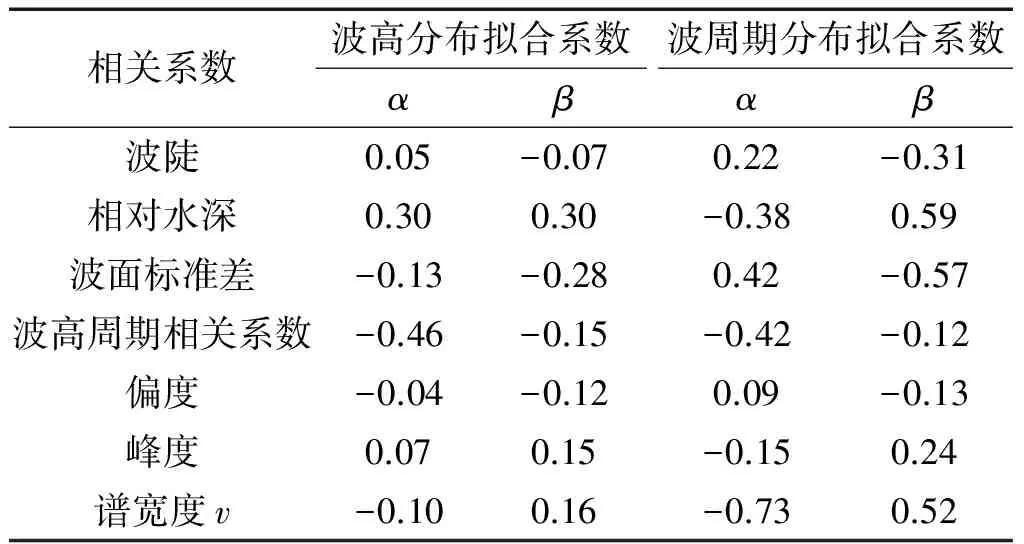
表1 威布尔拟合系数与有关参数的关系Tab.1 Correlation coefficients of Weibull fitting coefficients and other parameters

4 参数影响分析

4.1 常规参数

由相对水深统计得出82%的数据得自深水状态，因此，水深对实测波高分布的影响并不明显。

波高分布通常与波陡(波高比波长)、相对水深(水深比波长)、波面标准差等等参数有关[12]，波周期分布与谱宽度有关，但本次的资料统计分析发现有不一致的情况出现，表1中列出了波高拟合系数、波周期拟合系数与有关参数的相关系数值。由表1可知，波高分布拟合系数α与相对水深以及波高周期相关系数均有弱相关关系，系数β与相对水深以及波面标准差均有弱相关关系，但α和β与这些参数不能形成良好线性或者曲线关系，两系数与其他参数的关系不明显。波周期分布的拟合系数α和β则明显与谱宽度有关，而与其他参数的相关性相对较差，这与理论周期分布公式(3)和(4)中采用谱宽度v作为基本参数一致，印证了谱宽度对周期分布曲线有明显的影响，与谱宽度v的关系具体见图5、图6，拟合得到如下公式

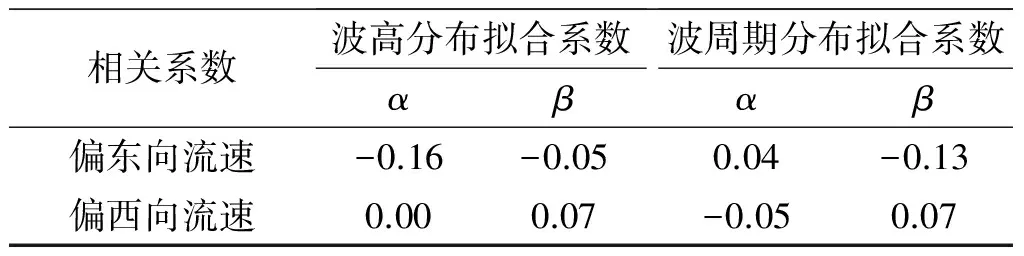
表2 威布尔拟合系数与流速的关系Tab.2 Correlation coefficients of Weibull fitting coefficients and flow velocity

α=26.22v2-33.99v+13.18

(5)

β=0.96v+0.29

(6)

因此，可根据上述公式(5)和(6)改进威布尔拟合得出的周期分布公式，改进前后的效果见图7和图8，改进后的拟合效果相对较好。统计分析还发现，在对多组实测数据的威布尔拟合分布分析中，在大周期比区域，威布尔拟合曲线偏低于实测值。

4.2 流速流向

流速、流向与分布的关系较为复杂，表1显示流速与系数并未有明显关系，但根据杭州湾地形区分流向为偏东向(45°～135°)和偏西向(225°～315°)，分别计算两个方向与分布系数的相关性，结果见表2，由此得出偏东向流速与波高分布拟合系数α和周期分布拟合系数β均有微弱关系，这说明钱塘江流入杭州湾向海的水流对波高和周期分布有微弱影响。偏西向流速与两分布的系数几乎无关，表明朝向钱塘江的涨潮流并未对波浪分布有明显影响。

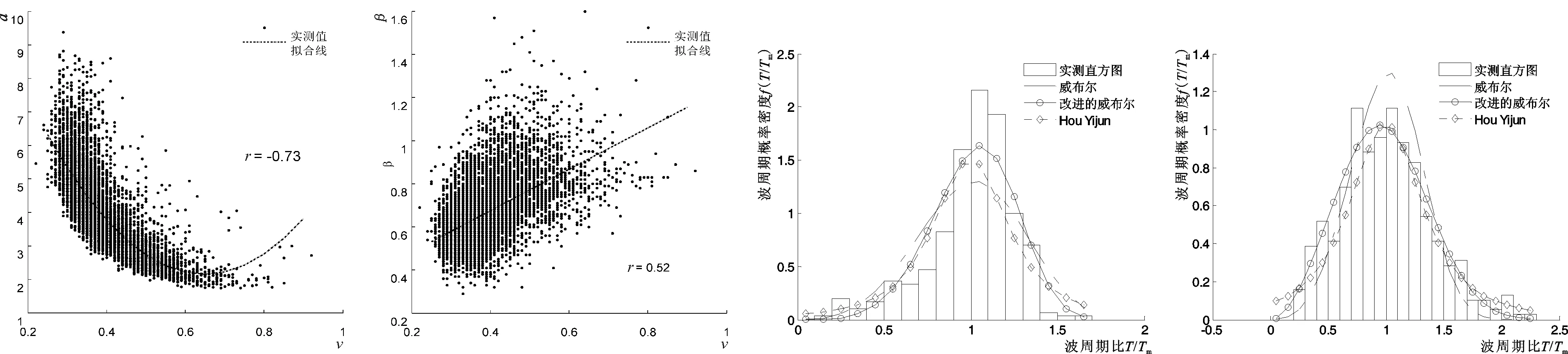
图5 谱宽度v与波周期拟合系数α的关系Fig．5Relationshipofspectralwidthvandwaveperiodcoefficientα图6 谱宽度v与波周期拟合系数β的关系Fig．6Relationshipofspectralwidthvandwaveperiodcoefficientβ图7 2009年06月25日16时实测波周期分布及拟合曲线Fig．7Distributionofmeasuredmeanwaveperiodat16：00onJune25，2009andtheory图8 2010年05月31日14时实测波周期分布及拟合曲线Fig．8Distributionofmeasuredmeanwaveperiodat14：00onmay31，2010andtheory

5 结论

(1) 对杭州湾中部的实测数据分析得出，冷空气引起的波浪过程强于莫拉克台风浪过程，绝大部分实测波高分布于平均波高3倍范围内，出现频率最高的波高为0.8～0.9倍的平均波高，理论波高分布与实测分布符合较好，其中威布尔分布拟合效果最好。

(2) 实测波周期分布主要集中于平均周期2.5倍范围内，出现频率最高的周期为1.0～1.1倍的平均周期，双参数威布尔分布与实测波周期分布符合相对较好，对威布尔系数进行改进可以得出更符合实测分布的效果。

(3) 实测波高周期联合分布的高发生概率区域位于平均波高和平均波周期及其附近，孙孚理论分布的趋势并不能代表实测分布。

(4) 实测波浪分布具有区域性特征，威布尔分布的拟合系数与相关参数的关系体现了杭州湾波浪分布特性的复杂性。

致谢：感谢海洋二所工程海洋学重点实验室测量和获取本文波浪资料的团队人员。

[1]王以谋,范顺庭,王兴德.黄河口“烂泥”波浪特性的分析[J].海洋科学, 1995,19(6):42-46.

WANG Y M, FANG S T, WANG X D. Analysis on wave characteristics at muddy sediment of yellow river estuary[J]. Marine Sciences, 1995,19(6):42-46.

[2]冯卫兵,仁华堂,洪广文.上海海域风浪谱分析与研究[J]. 河海大学学报, 2002,30(3):28-32.

FENG W B, RENG H T, HONG G W. Representation of Sea Wave Spectra for Shanghai Seas[J]. Journal of Hohai university, 2002,30(3):28-32.

[3]茹荣忠,蒋胜利.杭州湾的波浪概况[J]. 东海海洋, 1985,3(2): 34-40.

RU R Z,JIANG S L. A Sketch of the Wave in the Hangzhou Bay[J]. Donghai Marine Science, 1985,3(2): 34-40.

[4]张伯虎,曹颖.钱塘江河口(杭州湾段)的自然特性分析[J]. 浙江水利科技, 2013,41(2):61-63.

ZHANG B H,CAO Y. Analysis of natural characteristics of Qian Tang River Estuary (Hangzhou Bay section)[J]. Zhejiang Hydrotechnics, 2013,41(2):61-63.

[5]束芳芳,叶小红,廖康明,等.广东阳西近岸海域波浪的分布特征[J]. 应用海洋学学报, 2012,31(3):324-331.

SHU F F,YE X H,LIAO K M,et al.Distribution characteristics of wave in the Guangdong Yangxi offshore[J]. Journal of Applied Oceanography, 2012,31(3):324-331.

[6]郭浩霖,宋育霖,张帆一,等.江苏近岸海域波浪的分布特征[J]. 水运工程, 2014 (5):41-47.

GUO H L,SONG Y L,ZHANG F Y, et al. Distribution characteristics of wave in Jiangsu offshore sea area[J]. Port & Waterway Engineering, 2014 (5):41-47.

[7]孙孚.海浪周期与波高的联合分布[J]. 海洋学报, 1988,10(1):10-15.

SUN F. The joint distribution of sea wave period and wave height[J]. Acta Oceanologica Sinica, 1988,10(1):10-15.

[8]Forristall G Z. On the statistical distribution of wave heights in a storm[J]. Journal of Geophysical Research Atmospheres, 1978,83(C5):2 353-2 358.

[9]Gluhovski B H. Distribution characteristics of wave parameters and changes in wave action with depth[J]. Reports St. Inst. Oceanology, 1968,93:98-111.

[10]Hou Yi-jun, Li M, Song G, et al. Distribution of the nonlinear random ocean wave period[J]. Chinese Journal of Oceanology and Limnology, 2009,27(4):919-923.

[11]俞聿修,柳淑学.石臼港海浪的统计特征和谱[J].港工技术,1989 (2):12-22.

YU Y X,LIU S X. Wave Statistical and spectral characteristics of Shijiu port[J].Port Engineering Technology,1989 (2)：12-22.

[12]吴月勇,陈国平,严士常,等.港域波浪联合绕射、反射特性试验研究[J].水道港口,2017(4):330-336.

WU Y Y, CHEN G P, YAN S C, et al. Experimental study on combined diffraction-reflection characteristics of harbor wave [J]. Journal of waterway and harbor, 2017(4):330-336.