不规则波作用下斜坡堤越浪的数值模拟
李东洋,张庆河,焦方骞
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
斜坡堤是保护沿海地区免受潮、浪袭击的重要水工建筑物,由于斜坡堤迎浪面较缓,波浪爬高往往较大,很容易发生越浪,因此准确模拟斜坡堤越浪过程并确定越浪量,对于斜坡堤的设计具有重要意义。
早期对斜坡堤越浪的研究主要以物理模型试验为主,王聪等[1]在总结前人物理模型试验的基础上,研究了不规则波作用下挡浪墙高度等对越浪量的影响。近年来,随着计算机技术和并行计算的发展,利用数值模型研究斜坡堤越浪成为港口海岸工程学科关注的热点。追踪自由表面运动的斜坡堤越浪数值模型主要分为两大类,一类基于N-S方程,如Van Gant等[2]较早基于二维不可压缩的N-S方程研究了波浪与宽肩台可渗斜坡堤相互作用的水动力特性,Losada等[3]基于体积平均的RANS方程和VOF方法建立了COBRAS(Cornell Breaking Waves and Structure)模型,模拟分析了不规则波在可渗斜坡堤上的越浪过程。关大玮[4]基于CFD软件Flow-3D建立三维数值波浪水槽,模拟研究了规则波和不规则波作用下不可渗光滑斜坡堤的越浪过程。闫科谛等[5]基于OpenFOAM软件建立数值波浪水槽,通过网格细化,刻画出栅栏板凹槽的形状,进而模拟了规则波作用下非可渗堤心栅栏板护面的斜坡堤越浪过程。Xiang等[6]等通过将Fluidity和Y3D耦合的方法,模拟研究了规则波作用下扭王块体护面斜坡堤周围的水动力特性。另外一类模型为无网格方法,如叶晓文[7]基于不可压缩SPH数学模型研究了规则波沿可渗斜坡堤的爬坡和越浪过程, Ren[8]基于弱可压的光滑粒子流体力学方法(WCSPH)模拟了波浪与可渗潜堤的相互作用,并分析了堤体内部的水动力特性。温鸿杰[9]基于改进的SPH方法,模拟研究了规则波在出水堤上的破碎和越浪过程。
总体上来看,目前关于斜坡堤越浪数值模拟的研究还主要集中于规则波,对护面块体进行三维全尺度模拟且考虑护面块体垫层以下可渗特性的工作也比较少见,这使得利用数值模型解决斜坡堤越浪等实际工程问题仍受到一定的制约。因此,利用数值模型展现真实海况下斜坡堤越浪过程,需要进一步探索。考虑到SPH类模型在压力脉动等方面还存在有待解决的问题,本文将利用Jesus[10]和Lara等[11]基于OpenFoam开源软件开发的ihFoam求解器,通过OpenFoam网格划分工具snappyHexMesh精细刻画网格的方法生成扭王字块,模拟不规则波作用下扭王块体护面斜坡堤越浪过程,以使斜坡堤越浪的数值模拟在解决工程问题时达到一定的实用性,为斜坡堤的设计提供依据。
1 控制方程与边界条件
1.1 控制方程
本文通过将渗流运动的Darcy-Forchheimer方程引入到两相流求解器interFoam中,生成全新的考虑孔隙介质流的ihFoam求解器,采用主动吸收式速度入口造波,通过求解体积平均的RANS方程,模拟水体和空气两相不可压缩流体的运动。紊流模型选用RNGk-ε模型,采用VOF法捕捉自由表面。模型控制方程如下
(1)
(2)
(3)
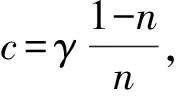
(4)
式中:D50为组成孔隙介质的中值粒径;KC=umT/(nD50),其中um为最大震荡速度;T为震荡周期。α和β分别为Darcy-Forchheimer线性项系数和非线性项系数,2011年Lara等[13]提出了α和β关于孔隙率和中值粒径的经验公式如下
(5)
当n=1时,即纯水体情况时,式(2)转化为标准的雷诺时均方程。

图1 数值水槽和边界条件示意图Fig.1 Numerical wave flume and boundary condition diagram
1.2 边界条件
数值水槽和边界条件示意图如图1所示,左侧入口设置为主动吸收造波边界。右侧出口设置为辐射消波边界。数值水槽前后侧边界设置为可滑移固边界,法向速度为0。底面及护面块体设置为固壁边界,数值边界条件设置为无滑移边界条件,壁面处的流速为0。
2 扭王块体护面斜坡堤越浪模拟
为了验证数值模型的合理性,我们收集已有物理模型试验数据与数值模型结果进行对比分析。
2.1 物理试验模型设置

图2 物理模型试验尺寸示意图[14]Fig.2 Physical model size diagram[14]
陈伟秋等[14]通过物模试验研究了不规则波作用下扭王块体护面斜坡堤的平均越浪量。试验是在长175 m、宽1.2 m、高1.5 m的波浪水槽中进行的,试验模型的具体尺寸如图2所示,斜坡堤左右两侧坡度均为1:1.5,堤顶高度为0.5 m,斜坡堤堤底宽为2.11 m,两端各有坡度为1:2的抛石棱体作为护底,海侧斜坡铺设一层扭王字块,单个扭王字块的高度是6 cm。试验水深0.4 m,入射波为不规则波,采用JONSWAP谱进行模拟,有效周期为2 s,有效波高分别为6.6 cm、7.1 cm、7.6 cm。
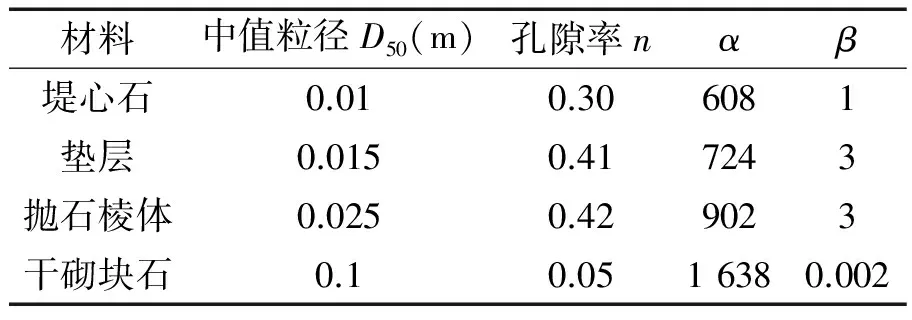
表1 多孔介质物理参数表Tab.1 Physical parameter of porous media
模拟过程中除扭王块体采用全尺度模拟外,斜坡堤堤体其他组成部分均作为孔隙介质处理,各层物理参数见表1。
2.2 三维数值水槽不规则波验证
试验中采用JONSWAP谱进行模拟,JONSWAP谱的表达形式为
(6)
(7)
(8)
(9)
式中:S(f)为波浪谱密度函数;Hs为有效波高;fp为谱峰周期;f为波浪频率;γ为谱峰因子,取3.3;σ是波浪密度的标准差,当f≤fp时,σ=0.07,当f>fp时,σ=0.09。

3-a 波面历时图 3-b 计算波谱与理论波谱对比图图3 Hs=7.1 cm情况下数值造波结果Fig.3 Hs=7.1 cm Simulation results of free surface
不规则波采用线性波叠加法生成[15],根据等分频率法将波浪能量分割成70份。因为数值模拟的侧壁采用的是可滑移边界条件,避免了壁面对内部流场的影响,所以可以利用宽度较窄的计算水槽反演试验结果,具体数值水槽设置如下:长15 m,高0.6 m,宽0.24 m,网格水平空间步长取L/100,为了准确追踪自由表面,在其静水位上下2倍有效波高范围内取30层网格,上下网格渐变,宽度方向上取15层网格。数值模拟时间为220 s,取x=12 m(即堤脚)处测点进行分析,以有效波高为7.1 cm为例,图3-a显示了其水位历时曲线。取后100个波,即20~220 s的实测数据进行快速傅里叶分析,得到不规则波浪的能量谱。图3-b显示了计算模拟波谱与理论波谱的对比情况,由图可知两者比较接近。模拟有效波高与理论有效波高误差为2.4%,满足《波浪模型试验规程》[16]要求。
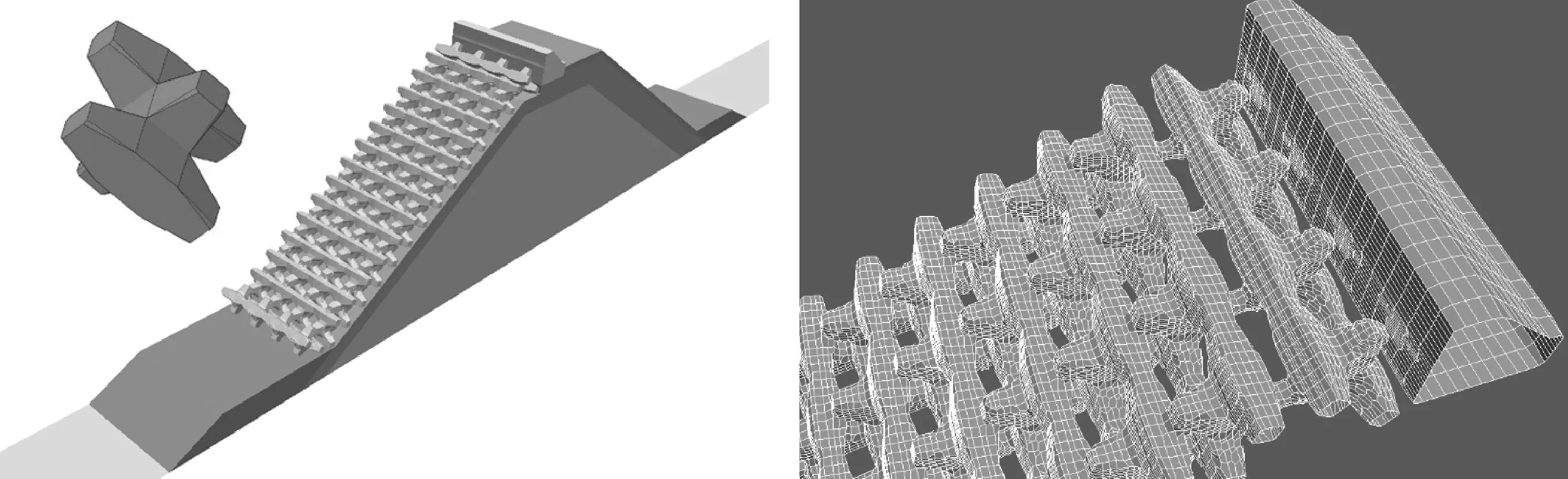
图4 AutoCAD三维建模中扭王字块及扭王字块排放示意图 图5 扭王块体和胸墙经snappyHexMesh处理后局部网格剖分示意图Fig.4 AutoCAD three-dimensional model of accropode blocks Fig.5 Accropode blocks and parapet local mesh encryption by snappyHexMesh
2.3 扭王块体全尺度模拟的网格刻画
OpenFOAM提供了强大的网格生成工具,通过自带的网格处理工具snappyHexMesh将扭王字块和胸墙转变成贴体网格模拟,可以逼近真实工况下斜坡堤上的波浪爬坡和越浪。
首先参照《防波堤设计与施工规范》[17]中规定的扭王字块的尺寸,使用AutoCAD三维建模绘制出扭王字块的外部轮廓。周雅等[18-19]通过物理模型试验研究得出扭王字块护面块体的排放型式对越浪量的影响,因此为了简化模型,将扭王字块规则排放在斜坡堤上,如图4所示。图5显示了精细网格刻画后的扭王块体和胸墙局部网格形状。由图可以看出数模所采用的网格能较好描述扭王护面块体和胸墙的外部形状。


6-a越浪量历时图6-b累计越浪量图图7 平均越浪量计算值与试验值比较图6 Hs=7.1cm情况下越浪量计算结果Fig.6Hs=7.1cmSimulationresultsofovertoppingdischargeFig.7Comparisonofnumericalaveragedischargeandexperimentalaveragedischarge
2.4 越浪模拟与试验结果的比较
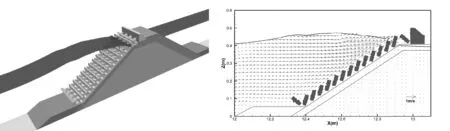
8-a t=174.36 s 9-a t=174.36 s
图6显示了有效波高为7.1 cm情况下的波浪越浪量历时图6-a和累计越浪量图6-b,在有效周期一定的情况下,越浪量随有效波高的增大而明显增大。取20~220 s(100个波)时间内的越浪量计算平均值以得到平均越浪量。图7显示了平均越浪量数值模拟结果与试验值的比较,由图可知斜坡堤越浪的数值模拟结果与试验结果吻合较好,表明利用snappyHexMesh网格处理工具生成贴体网格的方法对扭王护面块体进行全尺度模拟,对垫层以下块石利用渗流模型模拟斜坡堤越浪可以获得较好的效果。
2.5 越浪过程和堤前附近流场分析
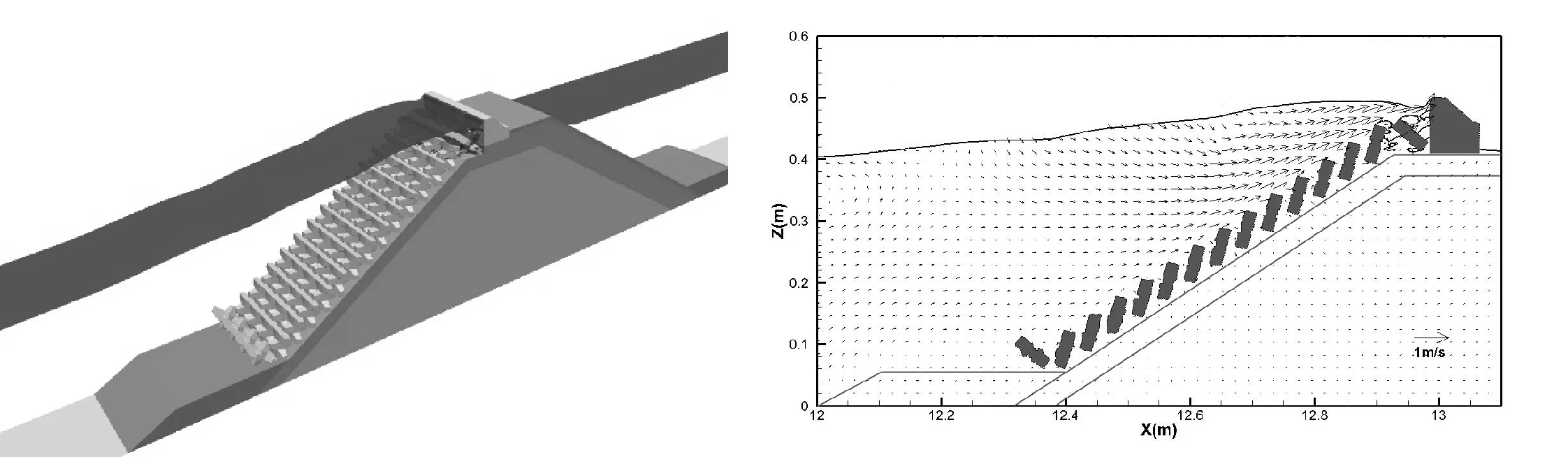
8-b t=174.56 s 9-b t=174.56 s
8-c t=174.76 s 9-c t=174.76 s图8 最大单波越浪过程三维示意图 图9 堤前附近流场图 Fig.8 3D process of the largest Fig.9 Variation diagram of single-wave overtopping velocity fields
图8显示了有效波高为7.6 cm,在174.5 s前后发生越浪时波面的三维过程,图9显示了Y=0.1 m,XZ剖面扭王字块附近的流场变化。从图中可以看出,越浪发生前,波浪沿着坡面向上爬升,在向上水体的带动下,水面抬高,波浪拍击胸墙表面,直至越过堤顶形成越浪。在整个越浪过程中,由于扭王字块护面的作用,堤内的渗流流速相对很小。
从越浪过程、越浪波面和流速变化过程看,本文所建立的模型较准确地反映了波浪与扭王块护面斜坡堤的相互作用,具备了为斜坡堤设计优化提供支持的能力。
表2模型与原型波要素
Tab.2 Wave elements under experimental model and prototype size

类别有效波高(m)有效周期(s)水深(m)实验室尺度0.07120.40原型尺度0.071×25=1.7752×251/2=100.40×25=10.00
2.6 原型工况的数值模拟
现阶段对于原型尺寸下的波浪与斜坡堤相互作用的研究,大多是通过比尺缩放,进行实验室物模试验,再将试验值根据《波浪模型试验规程》换算成原型,而直接研究原型尺寸下斜坡堤越浪的工作还比较少。因此,为进一步论证模型可否应用于描述现场尺度条件下的斜坡堤越浪,首先依据《波浪模型试验规程》[16]将文献[14]中的物理模型试验按照1∶25的比尺放大成原型工况,通过模拟该尺度下的斜坡堤越浪,并与文献[14]按照重力相似计算得出的越浪量进行比较,从而验证模型是否可用于模拟计算现场尺度下的斜坡堤越浪。以模型有效周期为2 s,有效波高0.071 m为例,按照重力相似准则确定原型波要素如表2所示。
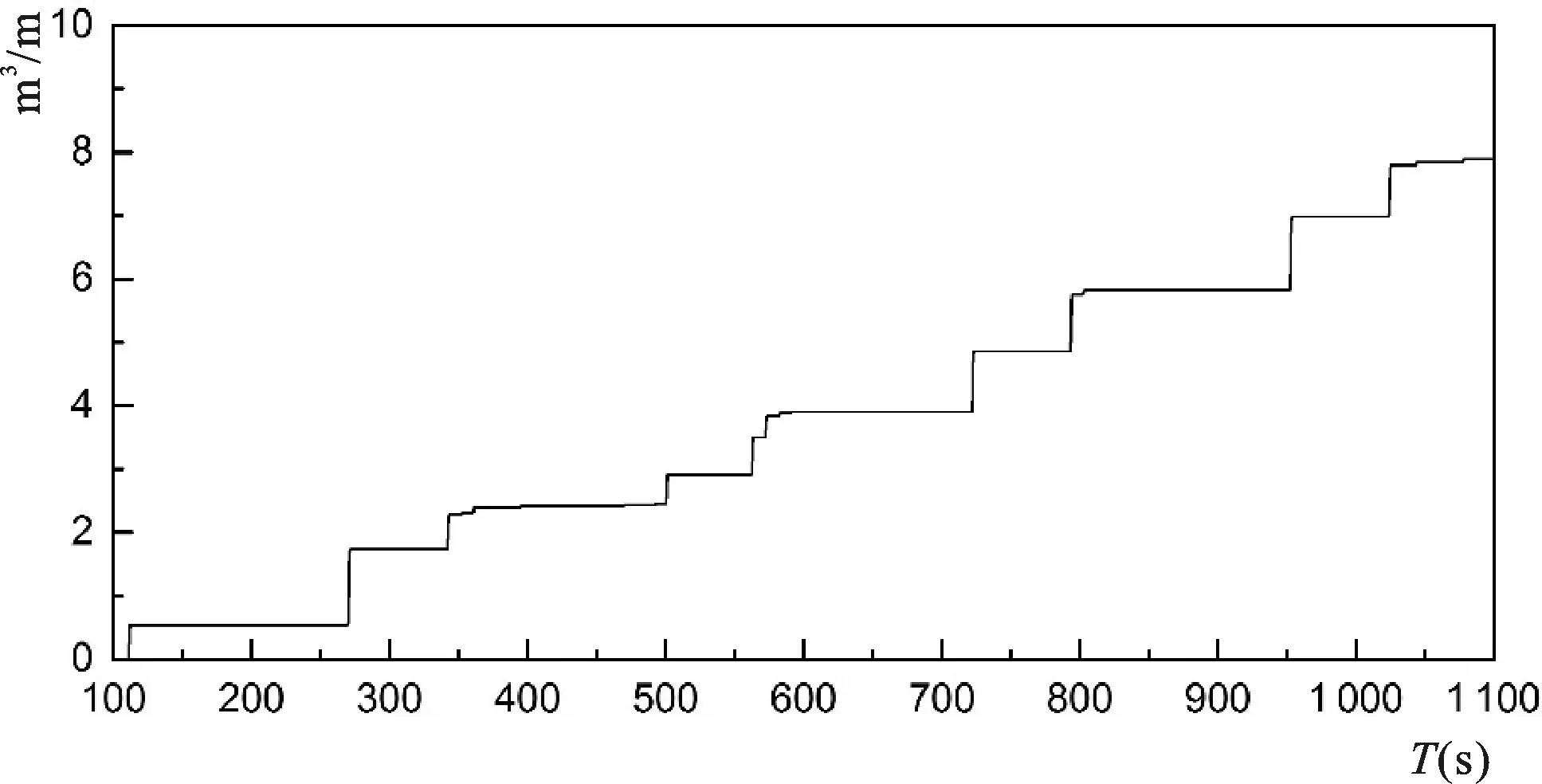
图10 原型工况下累计越浪量Fig.10 The accumulated overtopping discharge under prototype size
原型模拟数值水槽长×宽×高=375 m×6 m×15 m,依然按照上述方法建模。图10显示了原型尺度下累计越浪量的数值模拟结果,单个越浪发生时其实历时很短,可以看成是一个瞬时过程,图中折线每次的抬升就代表发生了一次越浪,“台阶”的高度即为单个越浪发生时的越浪量,从而可以得出,单波最大越浪量发生在950 s左右,单波最大越浪量约为1.3 m3/m。取100~1 100 s(100个波)时间内的越浪量计算平均值得到平均越浪量,原型尺度下数值计算的越浪量为7.89×10-3m3/m/s。根据模型试验越浪量折算到原型的平均越浪量为6.68×10-5×251.5=8.36×10-3m3/m/s,与原型数值模拟结果较为接近。合理的模型试验可以反映原型结果是比较公认的,因此,从原型直接模拟结果与模型试验折算到原型的越浪量比较吻合来看,利用OpenFOAM直接模拟原型工况下的斜坡堤越浪是可行的,并推荐采用原型尺寸进行数值研究,进而优化确定设计阶段中斜坡堤的断面型式和顶高程等。
3 结语
本文基于OpenFOAM建立数值波浪水槽,控制方程采用了体积平均的RANS方程和包含非线性项的渗流方程描述斜坡堤内部的水体渗流流动。利用AutoCAD三维建模绘制出扭王块体的外部轮廓,利用snappyHexMesh网格划分工具对斜坡堤扭王护面块体进行全尺度网格精细划分。采用建立的模型模拟研究了正向入射不规则波与扭王块体护面斜坡堤的相互作用,模拟结果表明,平均越浪量的计算值与实验结果吻合较好。通过将实验室尺度放大成原型尺度,模拟研究了原型条件下的斜坡堤越浪,从计算结果可以看出,平均越浪量的计算值与模型通过重力相似准则折算成原型的结果较为吻合。从实验室尺度和原型尺度模拟结果看,对护面块体进行全尺度模拟的数值波浪水槽目前已可以较为合理地描述复杂护面块体斜坡堤的越浪过程,可以应用于设计阶段对斜坡堤断面型式和顶高程的优化确定。
需要指出的是,本文仅给出了波浪正向入射情况下斜坡堤的越浪模拟结果,有关护面块体本身的稳定性以及斜向入射波与斜坡堤的相互作用有待进一步研究。
[1]王聪, 陈国平, 严士常, 等. 不规则波作用下斜坡堤越浪量试验研究[J]. 水运工程, 2017(2): 49-52.
WANG C, CHEN G P, YAN S C,et al. Experimental study on wave overtopping of sloping seawall under irregular wave action[J]. Port & Waterway Engineering, 2017(2): 49-52.
[2]Van Gent M R A. Wave action on and in permeable structures[D]. The Netherlands: Delft University, 1995.
[3]Losada I J, Lara J L, Guanche R, et al. Numerical analysis of wave overtopping of rubble mound breakwaters[J]. Coastal Engineering, 2008, 55(1): 47-62.
[4]关大玮. 规则波与不规则波的海堤越浪数值模拟[D]. 广州:华南理工大学, 2016.
[5]闫科谛, 张庆河. 栅栏板护面斜坡堤越浪数值模拟研究[J]. 中国港湾建设, 2016, 36(2):16-19.
YAN K D, ZHANG Q H. Numerical simulation of overtopping on sloping dike with fence panels[J]. China Harbour Engineering, 2016, 36(2):16-19.
[6]Xiang J, Latham J P, Vire A, et al. Coupled fluidity/Y3D technology and simulation tools for numerical breakwater modelling[J]. Coastal Engineering Proceedings, 2012, 1(33):66.
[7]叶晓文. 斜坡式防波堤越浪过程的SPH模拟[D]. 大连:大连理工大学, 2011.
[8]Ren B, Wen H, Dong P, et al. Improved SPH simulation of wave motions and turbulent flows through porous media[J]. Coastal Engineering, 2016, 107: 14-27.
[9]温鸿杰. 非线性波浪与可渗结构相互作用的SPH模型[D]. 大连:大连理工大学, 2016.
[10]Jesus M D, Lara J L, Losada I J. Three-dimensional interaction of waves and porous coastal structures. Part I: Numerical model formulation[J]. Coastal Engineering, 2012, 64:57-72.
[11]Lara J L, del Jesus M, Losada I J. Three-dimensional interaction of waves and porous coastal structures. Part II: Experimental validation[J]. Coastal Engineering, 2012, 64: 26-46.
[12]Higuera P, Lara J L, Losada I J. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM?. Part I: Formulation and validation[J]. Coastal Engineering, 2014, 83: 243-258.
[13]Lara J L, Losada I J, Maza M, et al. Breaking solitary wave evolution over a porous underwater step[J]. Coastal Engineering, 2011, 58(9):837-850.
[14]陈伟秋, 陈凌彦, 王登婷,等. 斜坡堤后坡砌石护面稳定厚度的模型试验研究[J]. 水运工程, 2016(6): 93-98.
CHEN W Q, CHEN L Y, WANG D T, et al. Experimental study on thickness of inner block revetment of sloped seawall[J]. Port & Waterway Engineering, 2016(6): 93-98.
[15]俞聿修, 柳淑学. 随机波浪及其工程应用[M]. 大连:大连理工大学出版社, 2011.
[16]JTJ/T234-2001,波浪模型试验规程[S].
[17]JTS154-1-2011, 防波堤设计与施工规范[S].
[18]周雅, 林登荣, 李庆银, 等. 不规则波作用下斜坡堤越浪量试验研究[J]. 水道港口, 2016(4):331-335.
ZHOU Y, LIN D R, LI Q Y, et al. Experimental research of wave overtopping on sloping dike under irregular waves[J]. Journal of Waterway and Harbor, 2016(4): 331-335.
[19]钟雄华,陈国平,严士常,等.不同摆放方式扭王字块体稳定性研究[J].水道港口,2016(5):479-483.
ZHONG X H, CHEN G P, YAN S C,et al. A stability analysis of different stack types of accropode[J]. Journal of waterway and harbor, 2016(5):479-483.

